A GENERIC METRIC FOR MEASURING COMPLEXITY OF

MODELS

Christian Schalles, John Creagh

Department of Computing, Cork Institute of Technology, Rossa Ave, Cork, Ireland

Michael Rebstock

Faculty of Economics and Business Administration, Hochschule Darmstadt University of Applied Sciences

Haardtring 100, 64295 Darmstadt, Germany

Keywords: Modelling, Complexity, Modelling Methods.

Abstract: In recent years, various object and process oriented modelling methods were developed to support the

process of modelling in enterprises. When applying these methods, graphical models are generated and used

to depict various aspects of enterprise architectures. Concerning this, surveys analyzing modelling

languages in different ways were conducted. In many cases these surveys include experimental data

collection methods. At this juncture the complexity of concrete models often affects output of these studies.

To ensure complexity value comparability of different models, a generic metric for measuring complexity of

models is proposed.

1 INTRODUCTION

Even though software and process modelling have

been used intensely over the last decades, only a

small number of research analyzed understandability

and comprehension of graphical models (Mendling

and Strembeck 2008). Past researches either were

focusing on process models or structural models. For

example, Mendling (2008) developed metrics for

process models such as Event Driven Process Chains

(EPC). Metrics in software engineering have shown

their potential as guidance to improve software

designs and make them more understandable and

easier to maintain (Vanderfeesten et al. 2007b).

Surveys focusing on the evaluation of modelling

languages include metrics measuring model

complexity in order to operationalize the influence

of model complexity on particular outputs. When

analyzing these studies it appears that a great

number of empirical researches apply easy

structured metrics for measuring the complexity of

models. Our paper focuses on the development of a

generic metric for measuring the complexity of

process models e.g. EPC as well as structure models

and UML class diagrams. Several researchers

concluded that business process and software

program designs have a lot in common (Reijers and

Vanderfeesten 2005), (Vanderfeesten et al. 2007a).

In general, this metric aims at researchers

conducting empirical surveys on modelling

languages.

2 GENERIC COMPLEXITY

METRIC

Before starting with metric development we analyze

essential properties of the complexity metric. We

reasoned that model size, semantic spread and

constructs connectivity are main properties for

evaluating model complexity. Hence, we take these

characteristics as a basis for our metric. In the

following each property is described.

2.1 Size

For developing a generic model complexity metric

we transform analogous partitions of complexity

metrics. Halstead (1977) and Mc Cabe (1976)

propose a set of metrics including primitive measure

values for measuring software complexity. Firstly, in

our approach we suggest to map model elements and

relations to the set of primitive measures proposed

436

Schalles C., Creagh J. and Rebstock M. (2010).

A GENERIC METRIC FOR MEASURING COMPLEXITY OF MODELS.

In Proceedings of the 12th International Conference on Enterprise Information Systems - Information Systems Analysis and Speciﬁcation, pages

436-439

DOI: 10.5220/0002874804360439

 SciTePress

by Halstead (1977) and Mc Cabe (1976). For

example the number of unique operators and the

number of operator occurrences are the number of

elements E and relations R in a model. With the size

S is dependent on E and R we can define following

formula:

S = (E

+ R

)

i=1

∑

(1)

2.2 Semantic Spread

Models developed in different domains and with

different methods differ very often not only

syntactically but also semantically (Pfeiffer 2007).

With focusing on the development of a generic

complexity metric we have to consider in particular

semantic complexity differences between models.

For measuring the semantic spread L of a concrete

model we introduce the two metrics number of

semantic different elements E

dif

and number of

semantic different relations R

dif

. In their approach

Recker and Dreiling 2007 choose these concepts for

measuring model complexity.

L = (E

dif

+ R

dif

)

i=1

∑

(2)

2.3 Connectivity

Beside size and semantic spread a further important

part of our metric is density. One essential element

for measuring model density is described by

connectivity degree of contained arcs and vertices

(Mendling 2008). In general, our developed

connectivity degree metric is based on Yang et al.

2006. For measuring the connectivity degree of

ontologies they propose the ratio of vertices and

arcs. With adding Henry and Kafura’s approach to

our metric we capture the complexity of element’s

connections to its environment (Henry and Kafura

1981). Hence, the fan-in and fan-out metric maps to

number of element inputs E

and number of element

outputs E

out

in a particular model. Finally, the

described concepts result in our formula for

measuring the connectivity degree c of various

models:

c = (E

+ E

Out

)

i=1

∑

/ E

i=1

∑

(3)

2.4 Generic Model Complexity Metric

In due consideration of different analyzed and

developed metric properties we are able to build up

our generic model complexity metric. Table 1

summarizes the above and gives an overview of

different metric properties and their source of

derivation.

Table 1: Overview of different model complexity metric

properties.

Derivation Extracted Components

Mc Cabe (1976), Halstead

(1977)

Number of elements E

Mc Cabe (1976), Halstead

(1977)

Number of relations R

Henry and Kafura (1981) Number of element inputs E

Henry and Kafura (1981)

Number of element outputs

out

(Recker and Dreiling 2007)

Semantic different elements

dif

(Recker and Dreiling 2007)

Semantic different relations

dif

Yang et al. (2006) Connectivity degree c

In the next step we have to merge the analyzed and

defined properties of model complexity for

developing an overall model complexity metric.

Thus, we propose the following formula for generic

measuring of model complexity C

= (S+ L

) *c

(4)

Our developed metric contains size S, semantic

spread L and connectivity degree c for measuring the

complexity of models. Considering the fact that

semantic spread increases user related complexity

more than model size we introduced squaring L.

Hence, L

weights semantic spread more than S of

particular model.

For example, the more different relationships (e.g.

generalization, aggregation etc.) are used in a class

diagram the higher the complexity of this model.

Root extraction over S+L

lowers value dispersion to

a significant level. Furthermore this result is

weighted with model connectivity degree.

2.5 Findings

In order to prove correctness and reliability of our

approach we are measuring the complexity of six

heterogeneous models with applying our generic

complexity metric. Therefore we choose models

with different complexity degrees. For proving the

generality of our metric we apply different structure

A GENERIC METRIC FOR MEASURING COMPLEXITY OF MODELS

437

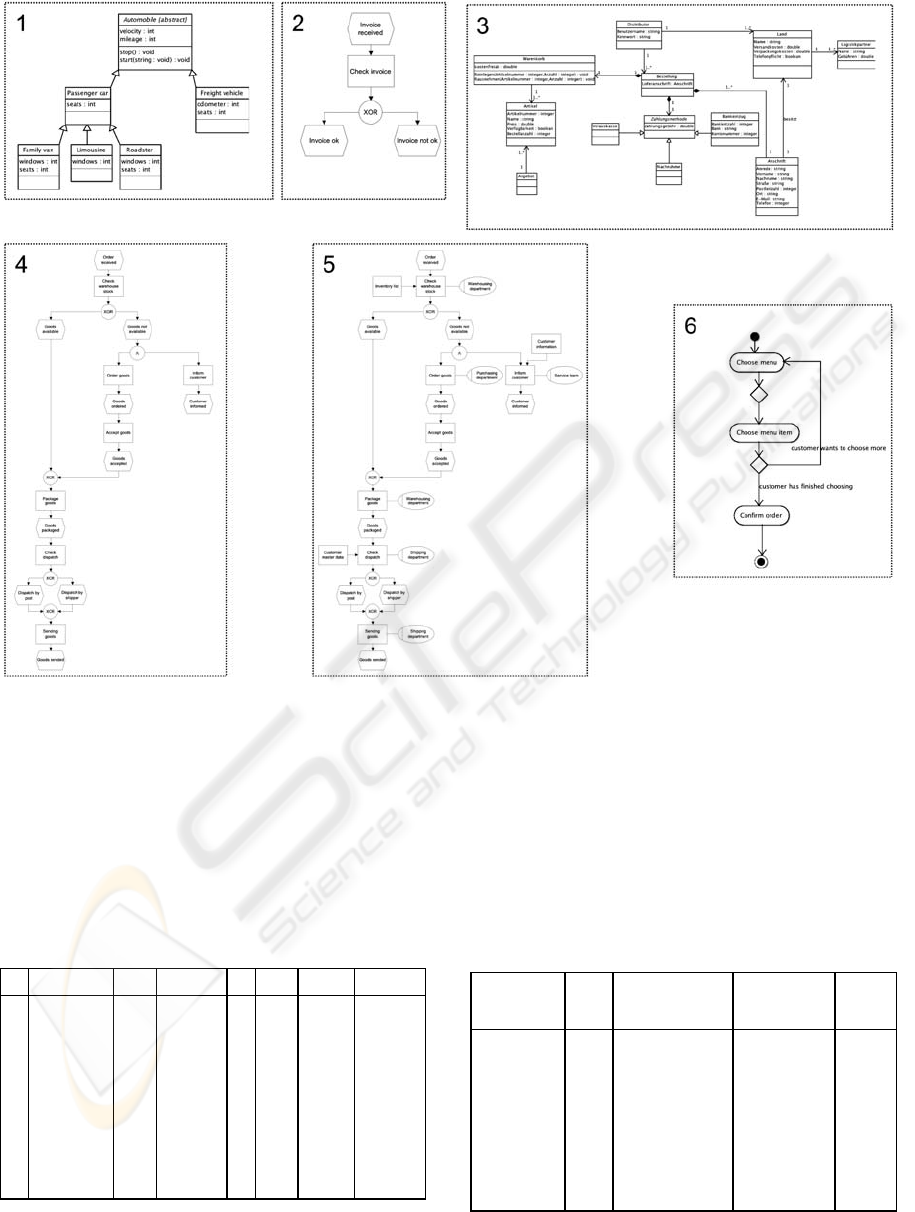
Figure 1: Applied models for proving metric correctness and reliability.

and process modelling languages. Figure 1 gives an

overview of the applied models. Table 2 shows

resulting variables E, E

out

, S, L and c with

applying our developed complexity metric C

. For

testing the correlation between metric results and

individual complexity evaluation we conducted a

survey on complexity of models. In this experiment

overall 20 modelling experts participated.

Table 2: Complexity evaluation with our metric.

Type E E

out

S L c C

Class

Diagram

6 10

3 1.67 7.45

EPC* 5 8 9 4 1.60 8.00

Class

Diagram

12 24

7 2,00 17,20

EPC* 22 46

5 2.09 17.49

eEPC** 31 59

8 1.90 21.45

Activity

Diagram

7 14

5 2.00 12.49

*Event driven Process Chain

**extended Event driven Process Chain

They were asked to evaluate the complexity of

models pictured in Figure 1 on a scale with extreme

values 1 and 10. The other values range in between.

Table 3 subsumes the survey complexity results C

the relative distribution of C

and C

and

additionally the difference D of C

and C

. As

shown in table 3 the difference D of C

and C

negligible.

Table 3: Comparison of metric and survey results.

Model

rel.

Distribution

rel.

Distribution

Class

Diagram I

2.3 0.09 0.08 0.01

EPC I 1.5 0.10 0.05 0.05

Activity

Diagram

2.8 0.15 0.09 0.06

Class

Diagram II

7.3 0.20 0.24 0.04

EPC II 7.7 0.21 0.25 0.04

EPC III 8.3 0.26 0.29 0.03

* values rounded

ICEIS 2010 - 12th International Conference on Enterprise Information Systems

438

Considering this strong relation between C

and

we assume that our metric highly correlates with

individual human model complexity evaluation.

3 CONCLUSIONS

With developing this metric we aim for supporting

empirical surveys on modelling languages.

Therefore we propose a metric analyzing and

comparing complexity of models developed with

different process and structure modelling languages.

It is important to consider semantic spread and

connectivity degree in addition to model size.

Considering generality of our approach we have to

mention some restrictions: To ensure generality we

solve this problem on an abstract graph-based level.

We are aware that an EPC-event, UML-activity and

UML-class are semantically different and cannot be

compared by implication. Hence, we built up our

metric focusing on graph theory i.e. arcs and

vertices. Subsequently we moved from abstract level

to concrete level adding semantic spread. Typical

application domains for our metric are empirical

surveys on modelling languages including model

complexity. Another domain is the practical

application of our metric in organizations. Currently

organizations are designing process and structure

models without considering model complexity and

understandability. As a result, it may happen that

simple business cases are modelled in a complex and

unsuitable way. This leads to lower

understandability and higher maintenance costs in an

organization. Applying our metric might result in

transparent models that are easy to understand for

interpreting users. Future research comprises the

application of our metric in an empirical survey

focusing on usability evaluation of modelling

languages. Furthermore it is planned to prove our

metric with complex models including reference

models.

REFERENCES

Halstead, M. H. 1977. Elements of Software Science

(Operating and programming systems series). New

York: Elsevier Science Inc.

Henry, S. and D. Kafura. 1981. "Software structure

metrics based on information flow." IEEE

Transactions on Software Engineering 7(5):510-518.

Mc Cabe, T. J. 1976. "A Complexity Measure." IEEE

Transactions on Software Engineering 2(4):308-320.

Mendling, J. and M. Strembeck. 2008. "Influence Factors

of Understanding Business Process Models."

Proceedings of the 11th International Conference on

Business Information Systems 7(1):142-153.

Mendling, Jan. 2008. Metrics for process models:

Empirical foundations of verification, error

prediction, and guidelines for correctness. Berlin,

Heidelberg, New York, NY: Springer.

Pfeiffer, D. 2007. "Constructing comparable conceptual

models with domain specific languages." In

Proceedings of the 15th European Conference on

Information Systems (ECIS2007). St.Gallen,

Switzerland.

Recker, Jan C. and Alexander Dreiling. 2007. "Does it

matter which process modelling language we teach or

use? An experimental study on understanding process

modelling languages without formal education " In

Australasian Conference on Information Systems, eds.

Mark Toleman, Aileen Cater-Steel and Dave Roberts.

Toowoomba: University of Southern Queensland.

Reijers, H. A. and I. Vanderfeesten. 2005. "Cohesion and

Coupling Metrics for Workﬂow Process Design."

Lecture Notes in Computer Science 3080(1):290-305.

Vanderfeesten, I., J. Cardoso, J. Mendling, H.A. Reijers

and W. Van der Aalst. 2007a. "Quality Metrics for

Business Process Models." In Workflow Handbook

2007, ed. L. Fischer. Lighthouse Point, Florida:

Workflow Management Coalition.

Vanderfeesten, I., J. Cardoso and H.A. Reijers. 2007b. "A

weighted coupling metric for business process

models." In The 19th International Conference on

Advanced Information Systems Engineering

(CAiSE'07). Trondheim, Norway.

Yang, Z., D. Zhang and C. YE. 2006. "Evaluation Metrics

for Ontology Complexity and Evolution Analysis." In

Proceedings of the IEEE International Conference on

e-Business Engineering IEEE Computer Society.

A GENERIC METRIC FOR MEASURING COMPLEXITY OF MODELS

439