CLUX
Clustering XML Sub-trees
Stefan Böttcher, Rita Hartel and Christoph Krislin
Univeristy of Paderborn, Computer Science, Fürstenallee 11, 33102 Paderborn, Germany
Keywords: XML Compression, Grammar-based Compression, XML Sub-tree Clustering.
Abstract: XML has become the de facto standard for data exchange in enterprise information systems. But whenever
XML data is stored or processed, e.g. in form of a DOM tree representation, the XML markup causes a huge
blow-up of the memory consumption compared to the data, i.e., text and attribute values, contained in the
XML document. In this paper, we present CluX, an XML compression approach based on clustering XML
sub-trees. CluX uses a grammar for sharing similar substructures within the XML tree structure and a clus-
ter-based heuristics for greedily selecting the best compression options in the grammar. Thereby, CluX al-
lows for storing and exchanging XML data in a space efficient and still queryable way. We evaluate diffe-
rent strategies for XML structure sharing, and we show that CluX often compresses better than XMill, Gzip,
and Bzip2, which makes CluX a promising technique for XML data exchange whenever the exchanged data
volume is a bottleneck in enterprise information systems.
1 INTRODUCTION
1.1 Motivation
XML is widely used in business applications and is
the de facto standard for information exchange
among different enterprise information systems. Ex-
amples include the SEPA standard for financial
transactions, the OTA standard for travel data, the
internal XML format being used to store MS Office
documents, and the BMEcat standard for product ca-
talogs. Whenever the amount of processed XML da-
ta is a bottleneck, applications can take advantage of
XML compression techniques that offer a more effi-
cient and compressed format for accessing the XML
data. Such a compressed XML data format should be
queryable, i.e., it should allow navigation operations
(as e.g. the evaluation of path queries), such that ap-
plications can work directly on the compressed data
format. This includes that e.g. compressed SEPA da-
ta or compressed product catalogs can be exchanged,
searched and evaluated by a query processor without
prior decompression.
There have been different contributions to the
field of XML compressors generating queryable
XML representations, that range from encoding-
based (Zhang, Kacholia, and Özsu, 2004) to schema-
based (Ng et al., 2006), (Werner et al., 2006) to
DAG-based (Buneman, Grohe, and Koch, 2003) to
grammar-based (Busatti, Lohrey, and Maneth, 2005)
compressed representations. We follow the gram-
mar-based XML compression techniques, and we
propose an XML compression technique, called
CluX. CluX, like BPLEX (Busatti, Lohrey, and Ma-
neth, 2005), has the advantages of grammar-based
compression, i.e.,
 it removes redundancies within the structure of
the XML file by sharing similar sub-trees and
therefore achieves a more space efficient in-
memory representation than standard XML re-
presentations as e.g. DOM.
 it provides similar navigation operations as
DOM directly on the compressed structure, i.e.,
without prior full decompression of the docu-
ment. Therefore, applications based on DOM
could be adapted with a minimal effort to work
on the CluX structure instead.
In comparison to BPLEX, CluX does not neces-
sarily compress XML trees in a bottom-up fashion,
i.e., CluX is more flexible in the way, how it cons-
tructs shared patterns being used in the grammar.
As the XML structure can be compressed with a
significantly higher compression ratio than text
nodes and attribute values within an XML docu-
ment, we follow the approach first taken by XMill
142
Böttcher S., Hartel R. and Krislin C. (2010).
CLUX - Clustering XML Sub-trees.
In Proceedings of the 12th International Conference on Enterprise Information Systems - Databases and Information Systems Integration, pages
142-150
DOI: 10.5220/0002877901420150
Copyright
c
 SciTePress

(Liefke and Suciu, 2000) and separate the compres-
sion of the XML structure from the compression of
the text nodes, the attributes and the white space
contained in the XML documents. For the text
nodes, attribute values and white space we use con-
tainer-based string compression techniques similar
to those used in XMill. However, the focus of our
contribution is on compression of the XML structure
as described within the remainder of the paper.
1.2 Contributions and Focus
of the Paper
This paper proposes an approach to clustering-based
XML compression, called CluX that provides a
modifiable clustering technique for generating opti-
mized small grammars representing the compressed
XML document. We have implemented and eva-
luated different clustering strategies for finding the
most promising sharing of similar sub-trees. Our re-
sults show that the CluX strategy ‘minimize edges’
provides best compression times and the strategy
‘Minimize succinct storage’ provide strongest com-
pression ratio.
For simplicity of this presentation, we restrict it
to XML documents containing only element nodes,
i.e. attributes are regarded as special element types.
Note however that our implementation can handle
full XML documents including attributes, text values
and white space etc., such that we can compress e.g.
SEPA data, OTA data, MS Office documents, and
product catalogs.
1.3 Paper Organization
The remainder of this paper is organized as follows.
Section 2 describes the basic concept of grammar-
based compression, i.e. how an XML tree can be
stored in a more space saving way by sharing similar
structures, and it explains how these shared struc-
tures can be represented by patterns being used in
tree grammars. Section 3 describes how the next pat-
terns to be shared can be determined by a cluster
analysis and discusses different clustering strategies.
Section 4 evaluates the presented clustering strate-
gies. Section 5 compares CluX to related work. Fi-
nally, Section 6 summarizes our contributions.
2 SHARING SIMILAR TREES
2.1 The Paper’s Example Document
XML compressors computing directed acyclic
graphs, DAGs, (Buneman, Grohe, and Koch, 2003)
are based on sharing identical sub-tree structures.
Whenever a sub-tree occurs repeatedly within an
XML document, a pointer to the first occurrence is
stored instead of storing the repeated sub-tree anoth-
er time. Instead of only sharing identical substruc-
tures, our approach follows the grammar-based
compression introduced in BPLEX (Busatti, Lohrey,
and Maneth, 2005) which is capable to share similar
sub-trees which differ in small parts.
The following example is being used not only for
explaining the difference between these sharing ap-
proaches, but also as a motivation why different
sharing techniques for similar sub-trees may lead to
different compression ratios.
Figure 1: Document tree of an XML document with re-
peated matches of patterns.
Figure 1 shows an example XML document
represented as a binary tree. This XML document
tree can be generated by the following grammar us-
ing the non-terminal S as the start symbol, i.e. the
right hand side of the grammar rule is a term
representing the pre-order notation of the binary tree
in Figure 1:
S  r(k1(b(c(d(,),e(,)),), k2(h(c(d(,),g(,)),),
k3(b(c(f(,),e(,)),), k4(h(c(f(,),g(,)),),
k5(b(c(i(,),e(,)),), k6(h(c(i(,),g(,)),),)))))),)
Grammar 1: Grammar corresponding to the binary tree of
Figure 1.
2.2 Used Notations
A term is either a null pointer (denoted by the sym-
bol ‘’) a terminal expression, a nonterminal expres-
sion, or a parameter (denoted by the symbol ‘_’).
A terminal expression is of the form t(fc, ns),
where tT is a terminal of the set T of terminal sym-
bols, and fc and ns are terms representing the first
child and the next sibling of t. A nonterminal ex-
pression is of the form nt(te1, …, ten), where nt 
NT is a nonterminal of the set NT of nonterminal
symbols, and te1, …, ten are terms. The sets T and
NT are disjoint, i.e., T  NT = {}.
CLUX - Clustering XML Sub-trees
143

A production rule of arity n, n≥0 is of the form
lhs
 pattern, where lhs, called the left hand side
consists of a nonterminal and a list of n parameters,
and the pattern is a term te different from ‘’ and
‘_’, and te including all the terms nested in te con-
tain the same n parameters.
A match of a pattern p is a term, where each of
the n parameters of p is substituted by a term.
In Grammar 1, b(c(…), ) is a terminal-expres-
sion that represents a node with label ‘b’, which has
a first-child with label ‘c’ and which does not have a
next-sibling (denoted by the term  representing the
null-pointer).
2.3 The Idea behind Sharing
Similar Trees
In general, when storing an XML document in a na-
vigatable form (e.g. as DOM tree), the edges are ex-
pensive to store. Using sub-tree sharing should lead
to less memory consumption compared to the sto-
rage of the original XML tree. Furthermore, reduc-
ing the number of edges allows bottom-up query
processing which relies on the number of edges to
process queries faster. That is why we attempt to re-
duce the number of edges in the compressed XML
format.
Approaches like binary DAG compression, that
share identical sub-trees T in an XML document D
replace repeated occurrences of T in D by e.g. re-
placing each occurrence of T in D with N and add-
ing a rule that defines N to be a nonterminal that
represents T.
In Grammar 1, there are two matches for each of
the five patterns d(,), e(,), f(,),g(,), i(,).
Therefore, these matches can be replaced by the
nonterminals D, E, F, G, and I respectively, such
that we get the following grammar:
S  r(k1(b(c(D,E),),k2(h(c(D,G),),
k3(b(c(F,E),),k4(h(c(F,G),),
k5(b(c(I,E),),k6(h(c(I,G),),)))))),)
D  d(,)
E  e(,)
F  f(,)
G  g(,)
I  i(,)
Grammar 2: Grammar corresponding to the binary DAG
of the XML tree of Figure 1 (b).
If we were only able to share identical sub-trees,
we would only find sub-trees of size 1 (consisting of
nodes d, e, f, g, or i respectively). So replacing the
repeated occurrence by a pointer would lead to no
decrease in the number of edges (we get 30 edges
for the original tree and for the DAG of the tree).
1
But if we look for structures, that are not iden-
tical but similar besides small differences, we find in
the document tree of Figure 1 two different patterns
shown in Figure 2(b), one pattern consisting of the
nodes with labels b, c, and e, and the other pattern
consisting of the nodes with labels h, c, and g re-
spectively. For each of the two patterns, there exist
three matches which are highlighted in Figure 2(a).
Although the matches of the patterns have identical
inner nodes, they cannot be shared in a DAG be-
cause they differ in the child nodes of the node with
label c.
Figure 2: (a) Example document of Figure 1 with repeated
patterns replaced by nonterminals. (b) Repeated patterns.
Figure 2 (b) shows a pattern consisting of the
nodes with the labels b, c, and e, where the node
with the label c is the first-child of the node with the
label b, the node with the label e is the next-sibling
of the node with the label c, and the node with the
label c has a first-child that may be different for each
use of the pattern. BC_E is the name of the nonter-
minal being used as a shortcut for this pattern in the
graph of Figure 2 (a). Furthermore, Figure 2 (b)
shows a similar pattern, consisting of nodes with the
labels h, c, and g. HC_G is the name for the nonter-
minal being used for this pattern in Figure 2 (a).
Figure 2(a) shows a compressed version of the same
document as in Figure 1 where each occurrence of a
pattern in Figure 1 is replaced with the nonterminal
corresponding to the pattern.
The compression achieved by replacing the re-
peated patterns with a nonterminal is that each edge
inside a pattern is stored only once, i.e. in the pat-
terns shown in Figure 2 (b), instead of three times
(in Figure 1). In this example, the compressed ver-
sion of the XML document sharing repeated patterns
shown in Figure 2 (a,b) contains only 22 edges whe-
reas the document in Figure 1 contains 30 edges.
Therefore, we expect a high benefit from sharing
similar sub-trees whenever the number of edges de-
termines XML query processing time or memory li-
mitations are the bottleneck of XML processing.
1
We assume that null pointers are represented by a special sym-
bol, , and therefore, do not generate an edge.
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
144

The idea behind grammar-based compression ap-
proaches like CluX is to not only share identical sub-
trees, but to share patterns, i.e. similar sub-trees that
differ in small details. For example, the sub-trees
having a root element with label ‘b’ in Figure 1 dif-
fer in one detail: the first-child of the element with
label ‘c’. The same difference occurs in the DAG
represented by Grammar 2.
Within Grammar 3 below, we express the pattern
BC_E of Figure 2(b) by one grammar rule with the
left hand side BC_E(_), where the parameter ‘_’ is
being used for referencing the different child node
names of the nodes with label ‘c’. This grammar rule
is being used e.g. when the term b(c(D,E),) in the
start rule of Grammar 2 is replaced with the term
BC_E(D) in the start rule of Grammar 3. Here,
b(c(D,E),) is called a match, and BC_E(D) is called
a corresponding instantiation of the pattern
BC_E(_). Similarly, Grammar 3 contains a rule that
introduces the nonterminal HC_G for the pattern
consisting of the nodes with the labels ‘h’, ‘c’, and
‘g’, and replaces each occurrence of this pattern in
Grammar 2 with the nonterminal HC_G. By apply-
ing these steps of grammar-based compression,
Grammar 3 is more compact than Grammar 2
representing the DAG:
S  r(k1(BC_E(D),k2(HC_G(D),
k3(BC_E(F), k4(HC_G(F),
k5(BC_E(F), k6(HC_G(I),)))))),)
BC_E(_)  b(c(_,e(,)),)
HC_G(_)  h(c(_,g(,)),)
D  d(,)
F  f(,),
I  i(,)
Grammar 3: A grammar sharing patterns b(c(_,e(,)),)
and h(c(_,g(,)),) contained in similar sub-trees of the
XML tree of Figure 1.
2.4 Different Sub-tree Sharing
Strategies
In contrast to the minimal binary DAG that is unique
and that can be computed bottom-up efficiently by
hashing all sub-trees that have been read, in general,
there exist several different patterns that can be
shared and sharing one pattern may exclude sharing
another pattern. For example, an alternative sharing
applied to the XML tree of Figure 1 is sharing three
patterns, i.e., (c,d), (c, f), and (c, i) which yields the
following compressed document (c.f. Figure 3)
represented by the grammar Grammar 4 below:
Figure 3: Sharing 3 patterns (c,d), (c,f), and (c,i).
S  r(k1(b(CD_(E),), k2(h(CD_(G),),
k3(b(CF_(E),), k4(h(CF_(G),),
k5(b(CI_(E),),k6(h(CI_(G),))))))),)
CD_(_)  c(d(,),_)
CF_(_)  c(f(,),_)
CI_(_)  c(i(,),_)
E  e(,)
G  g(,)
Grammar 4: A grammar sharing patterns c(d(,),_),
c(f(,),_), and c(i(,),_) contained in similar sub-trees of
the XML tree of Figure 1.
Grammar 4 has 27 edges (in contrast to 22 edges
for the sub-tree sharing shown in Figure 2 and
Grammar 3). Note that Grammar 4 prevents sharing
of e.g. the nodes with labels b and c. So the cluster-
ing strategy, i.e. the sequence of steps sharing simi-
lar sub-trees influences the achieved compression ra-
tio.
BPLEX is a compressor that parses the grammar
representing the minimal DAG and searches bottom-
up for multiple non-overlapping occurrences of pat-
terns. Therefore, in our example, BPLEX will yield
the tree grammar Grammar 4. In contrast, our ap-
proach computes all possible candidates for a pattern
occurring multiple times within a given window. For
each of the candidate patterns, our approach calcu-
lates the benefit that is achieved when the candidate
pattern is shared with the help of a parameterized
tree grammar rule in order to decide which candidate
should be shared first. Therefore, our CluX approach
also considers Grammar 3.
3 FINDING PROMISING SHARES
3.1 Patterns - Clustering Similar
Sub-trees
The strategy of CluX for further compressing a
DAG by sharing similar sub-trees consists of an ini-
tialization step and several sharing steps on produc-
tion rules. In the initialization step, we start with a
set of minimal production rules, i.e., for each non-
leaf element ‘e’ with label ‘l’ occurring in the DAG,
CLUX - Clustering XML Sub-trees
145

we compute a production rule of the form A1( _, _)
 l( _, _) that produces an element with label l and
two parameters representing the first-child and the
next-sibling of e. The start production rule S con-
tains the whole structure of the binary XML tree, but
each label of a non-leaf node in the binary XML tree
is replaced with the nonterminal of the production
rule introduced for this non-leaf element. For exam-
ple, the start production rule S generated for the
DAG of the XML tree of Figure 1 given in Grammar
2 is transformed into the start production rule S of
the following grammar Grammar 5:
SAr(Ak1(Ab(Ac(D,E),),Ak2(Ah(Ac(D,G),),
Ak3(Ab(Ac(F,E),),Ak4(Ah(Ac(F,G),),
Ak5(Ab(Ac(I,E),), Ak6(Ah(Ac(I,G),),)))))),)
Ar(_, _)  r( _, _ ) .
Ak1( _, _)  k1( _, _ ) .
...
Ac( _,_)  c( _, _ ) .
D  d(,)
E  e(,)
F  f(,)
G  g(,)
I  i(,)
Grammar 5: After initialization, each non-leaf DAG node
of Grammar 2 is substituted with a production rule.
Our approach to sharing similar substructures
within an XML document was inspired by cluster-
ing. Clustering groups similar objects, where simi-
larity of objects is measured by using a distance
function d. Depending on the distance function d,
this process results in different clustering techniques
and different clustering results.
Similarly, in each sharing step, we search within
the start rule S and all other rules for matching pat-
terns p1, …, pn that can be shared by introducing a
new production rule. In order to find the patterns, the
sharing of which achieves the highest benefit, we
examine all matches of a possible pattern within the
production rules as follows. For example, look at the
nesting of nonterminals in the start rule of Grammar
5. Each of the patterns Ac(_,E) and Ac(_,G), where
the parameter ‘_’ matches anything, occurs three
times, i.e. has three matches in the start rule,
whereas e.g. the pattern Ac(D,_) occurs only twice,
i.e. has two matches in the start rule. Each clustering
distance function d calculates the benefit of applying
each of these different possible patterns based on
substituting their matches with their corresponding
instantiations (as defined in Section 2.3.) and finally
use that pattern that achieves the highest benefit.
We follow a greedy approximation, as in each
step, we implement that pattern that ‘locally’
achieves the highest benefit, which will in general
not necessarily lead to the highest ‘global’ benefit.
The benefit is negative, if storing a rule LP for
a pattern P needs more space than the replacement of
the matches of P by their instantiations saves within
all production rules.
However, when the benefit is positive, we store a
rule L P and we replace all matches of P within all
production rules with their corresponding instantia-
tions. We repeat this optimization step until no more
patterns with positive benefit can be found.
For example, starting with Grammar 2, we will
first find the matches C(D,E), C(F,E), and C(I,E)
that all have an edge connecting nodes with labels C
and E and match the pattern C(_,E). As no other
possible pattern achieves a higher benefit, we add
the production rule C_E C(_,E) to the set of pro-
ductions and, within the start rule, replace the match
C(D,E) by the instantiation C_E(D), the match
C(F,E) by the instantiation C_E(F), and the match
C(I,E) by the instantiation C_E(I). Within the next
iteration, we find the matches B(C_E(D),),
B(C_E(F),), and B(C_E(I),) which all have an
edge connecting nodes with label B to nodes with
label C_E. The production rule BC_E(_)
B(C_E(_),) is added and the above given mat-
ches are replaced by BC_E(D), BC_E(F), and
BC_E(I), as can be seen in Grammar 3.
Finally, for those production rules for which stor-
ing the rule has a negative benefit, we delete the rule
and replace each occurrence of a rule instantiation
with a corresponding instantiation of the right-hand
side of the production rule.
3.2 Clustering Strategies
Similarly, as clustering strategies depend on a con-
crete distance function d, the ‘quality’ of our CluX
clustering strategies depends on what we count. We
have implemented 4 different clustering strategies
that influence the choice of patterns to be shared and
have evaluated them, in order to find out, which
strategy achieves the highest compression ratio and
which strategy achieves the smallest runtime. These
strategies are called ‘minimize edges’, ‘minimize
rule size’, ‘minimize succinct storage’ and ‘random’
and are described in the following subsections.
3.2.1 Minimize Edges
For each possible pattern PP, we count the number
of matches within all rules. That pattern PP that has
the most matches is chosen for the next optimization
step, i.e., a new rule is LPP is added to the rule
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
146

system and each match of PP is substituted with a
corresponding instantiation of L. By applying the
substitution steps, the number of occurrences of pat-
terns may have to be adjusted, in order to determine
the frequencies of patterns for the next substitution
step. This is the strategy that locally minimizes the
number of edges in each step.
3.2.2 Minimize Rule Size
For each possible pattern PP, we calculate the stor-
age savings achieved by adding a rule L PP and
substituting each match of PP with a corresponding
instantiation of L. For this purpose, we compute the
memory required for storing a rule L  PP by sum-
ming up
 the number of nonterminals within PP
 the number of terminals within PP
 the number of parameters, i.e. the arity, of L
 1 (for the nonterminal defining the left-hand
side of the rule)
and we subtract the space needed to store the rule
from the space savings gained by substituting each
match of the pattern PP with a corresponding instan-
tiation of L. That new rule L  PP that leads to the
largest savings is chosen in each step. This strategy
does not consider that the storage costs may be less
when using a succinct storage format for grammar
rules.
3.2.3 Minimize Succinct Storage
As with the previous strategy, for each possible pat-
tern PP, we calculate the storage savings achieved
by adding a rule L PP and substituting each match
of PP with a corresponding instantiation of L. But in
contrast to the strategy ‘minimize rule size’, we do
not count the number of symbols and parameters
used in each rule, but we calculate the costs based on
the used succinct storage format of the compressed
grammar. In the following evaluation, we used the
same succinct format that has been used for BPLEX
(Fisher and Maneth, 2007).
3.2.4 Random
From the set of all possible patterns PP, we ran-
domly choose one. Only those possible patterns PP
are considered that decrease the total grammar size.
This strategy is being used as a benchmark for mea-
suring the quality of the other strategies.
4 EVALUATION
In a series of measurements, we compared the dif-
ferent clustering strategies ‘minimize edges’, ‘mi-
nimize rule size’, ‘minimize succinct storage’ and
‘random’ and the bottom-up clustering strategy of
BPLEX, concerning the compression ratio in terms
of edges and concerning the compression time. In
this series of measurements, we considered only the
structure of the datasets, i.e., we ignore all text data
(text nodes and attribute values) as text compression
is independent of the compared approaches to XML
structure compression.
We have evaluated CluX on the following datasets:
 1998statistics (1998 – 656 kB) –Baseball statis-
tics of the year 1998
 catalog-01 (C1 – 10.4 MB), dictionary-01 (D1
– 10.4 MB) – XML documents that were gener-
ated by the XBench benchmark
 hamlet (H – 273 KB) – an XML version of the
famous Shakespeare play
 JST_snp.chr (JST- 35.5 MB) – XML data on
the tumor suppressor gene JST
 NCBI_gene.chr (NCBI – 23.0 MB) – XML
data from the National Center for Biotechnical
Information
 Treebank (TB – 51.9 MB) – an XML docu-
ment representing a parsed text corpus
 XMark (XM – 111.1 MB) – an XML document
that models auctions
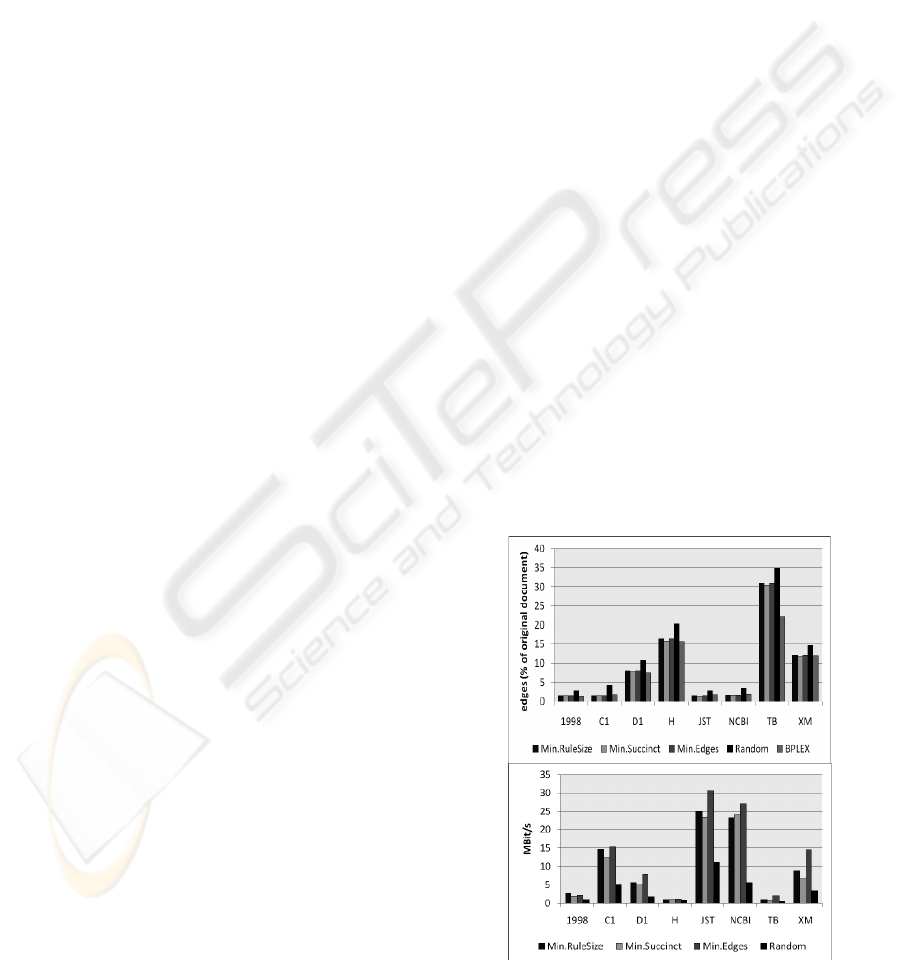
Figure 4: The different strategies compared by (a) com-
pression ratio of edges and (b) compression time.
CLUX - Clustering XML Sub-trees
147

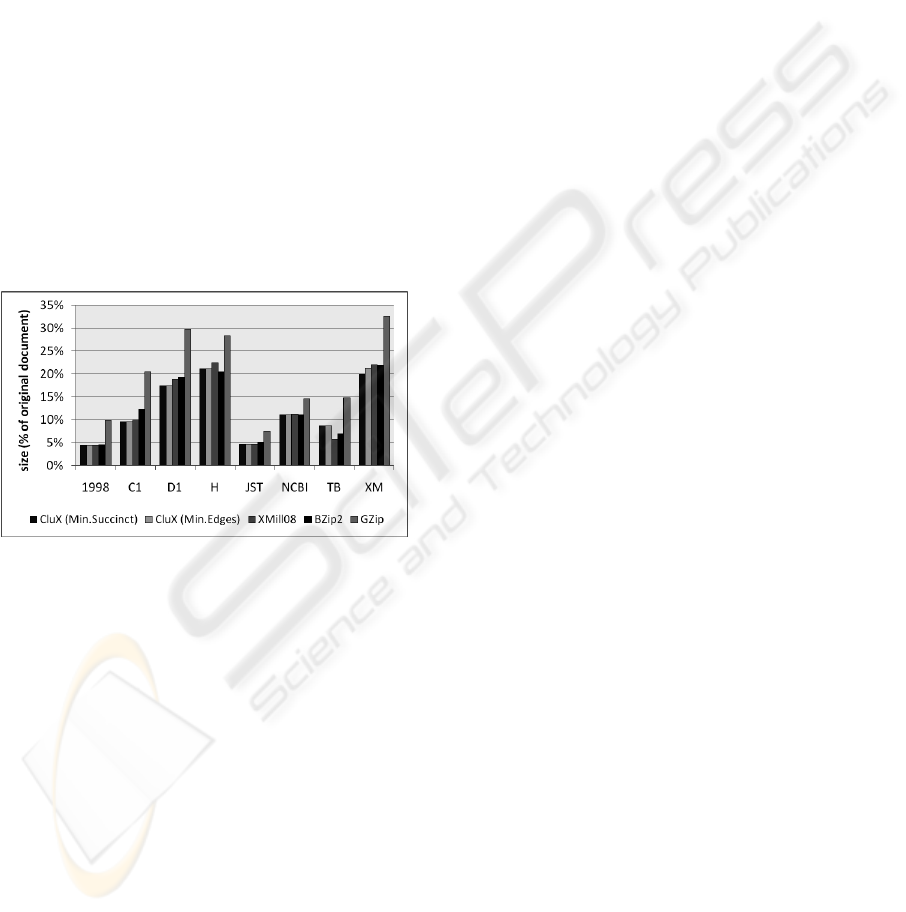
Figure 4 shows the evaluation results of the dif-
ferent clustering strategies compared by (a) the
compression ratio achieved for the number of edges
occurring in the compressed XML document and by
(b) the compression time respectively. BPLEX and
‘minimize succinct storage’ have shown to reach the
best compression ratio reaching a decrease of edges
to 8-9% of the number of edges occurring in the
original XML file on average, whereas ‘minimize
edges’ has shown to reach the fastest compression
time, reaching a throughput rate of 12.6 MBit/s on
average.
In a second series of measurements, we com-
pared the two strategies ‘minimize succinct storage’
and ‘minimize edges’ in combination with BZip2 to
compress the text data (i.e., text nodes and attribute
values) with three other approaches: first, gzip – a
generic compressor based on Huffman encoding and
LZ77, second, BZip2 - a generic compressor based
on Burrows-Wheeler-Transformation, third, XMill
(Liefke and Suciu, 2000) – an XML compressor us-
ing BZip2 for the compression of constant values.
Figure 5: Compression ratio as file compressors.
On average, both CluX strategies ‘minimize suc-
cinct storage’ and ‘minimize edges’ compress best
(c.f. Figure 5), followed by XMill followed by
BZip2 and finally followed by GZip.
When looking at the evaluation times, Gzip
reaches the fastest compression with a compression
throughput of more than 200 MBit/s on average, fol-
lowed by BZip2 and XMill reaching a throughput of
more than 35 MBit/s on average, finally followed by
the two CluX strategies reaching a throughput of
around 3 MBit/s on average. A similar trend can be
seen for the decompression, where GZip reaches a
decompression throughput of more than 1750
MBit/s on average, followed by BZip2 and XMill
reaching a throughput of 430 and 270 MBit/s on av-
erage, finally followed by the two CluX strategies
reaching a throughput of 19.5 MBit/s on average.
5 RELATED WORK
Besides generic compressors like gzip, bzip2 or 7zip
(based on LZMA) that all do not allow for query
evaluation on the compressed data directly, there
exist several approaches to XML structure com-
pression. XML structure compression can be mainly
divided into three categories: encoding-based com-
pressors, schema-based compressors and grammar-
based compressors. All these approaches differ in
their features, particularly in whether the com-
pressed data structures can be decompressed partial-
ly, whether the compressed data structures are que-
ryable, and whether they support unbounded XML
data streams.
Encoding-based compressors allow for a much
faster compression than the other compressors, as
only local data has to be considered in the compres-
sion instead of considering different sub-trees as in
grammar-based compressors.
The XMill algorithm (Liefke and Suciu, 2000) is
an example of the first category. The structure is
compressed, by assigning each tag name a unique
and short ID. Each end-tag is encoded by the symbol
‘/’. This approach does not allow querying the com-
pressed data.
XGrind (Tolani and Hartisa, 2002), XPRESS
(Min, Park, and Chung, 2003) and XQueC (Arion et
al., n.d.) are extensions of the XMill-approach. Each
of these approaches compresses the tag information
using dictionaries and Huffman-encoding (Huffman,
1952) and replaces the end-tags by either a
‘/’symbol or by parentheses. All three approaches al-
low querying the compressed data, and, although not
explicitly mentioned, they all seem to be applicable
to data streams.
Approaches (Bayardo et al., 2004), (Cheney,
2001), and (Girardot and Sunderesan, 2000) are
based on tokenization. (Cheney, 2001) replaces each
attribute and element name by a token, where each
token is defined when it is used the first time.
(Bayardo et al., 2004) and (Girardot and Sunderesan,
2000) use tokenization as well, but they enrich the
data by additional information that allows for a fast
navigation (e.g., number of children, pointer to next-
sibling, existence of content and attributes). All three
of them use a reserved byte to encode the end-tag of
an element. They are all applicable to data streams
and allow querying the compressed data.
The approach in (Zhang, Kacholia, and Özsu,
2004) defines a succinct representation of XML that
stores the start-tags in form of tokens and the end-
tag in form of a special token (e.g. ‘)’). They enrich
their compressed XML representation by some addi-
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
148

tional index data that allows a more efficient query
evaluation. This approach is applicable to data
streams and allows querying of compressed data.
Similarly, the approach presented in (Arroyuelo et
al., 2010) defines a succinct representation that
stores parentheses representing start and end tags to-
gether with a stream of symbols representing the tag
names. It is combined with a BWT-based compres-
sion technique for the constant data that allows ran-
dom access to the compressed data. This approach is
applicable to data streams and allows querying of
compressed data.
Schema-based compression comprises such ap-
proaches as XCQ (Ng et al., 2006), XAUST (Sub-
ramanian, and Shankar, 2005), Xenia (Werner et al.,
2006) and DTD subtraction (Böttcher, Steinmetz,
and Klein, 2007). They subtract the given schema
information from the structural information. Instead
of a complete XML structure stream or tree, they on-
ly generate and output information not already con-
tained in the schema information (e.g., the chosen al-
ternative for a choice-operator or the number of
repetitions for a ‘*’-operator within the DTD). These
approaches are queryable and applicable to XML
streams, but they can only be used if schema infor-
mation is available.
XQzip (Cheng and Ng, 2004) and the approaches
presented in (Adiego, Navarro, and de la Fuente)
and (Buneman, Grohe, and Koch, 2003) belong to
grammar-based compression. They compress the da-
ta structure of an XML document by combining
identical sub-trees. Afterwards, the data nodes are
attached to the leaf nodes, i.e., one leaf node may
reference several data nodes. The data is compressed
by an arbitrary compression approach. These ap-
proaches allow querying compressed data, but they
are not directly applicable to infinite data streams.
The approach presented in (Böttcher, Hartel, and
Messinger, 2009) and BSBC (Böttcher, Hartel, and
Heinzemann, 2009) combine encoding-based and
grammar-based compression (BSBC) or schema-
based and grammar-based compression (Böttcher,
Hartel, and Messinger, 2009) respectively. Instead of
an XML document, a DAG that summarizes the
structure of the XML document is taken as input and
is compressed further either by encoding a succinct
representation of the tree structure of the DAG
(BSBC), or by subtracting schema information from
the tree structure of the DAG. These approaches al-
low querying of compressed data and are directly
applicable to infinite data streams, as the backward
edges within the DAG are only generated within a
given window size.
An extension of (Buneman, Grohe, and Koch,
2003) and (Cheng and Ng, 2004) is the BPLEX al-
gorithm (Busatti, Lohrey, and Maneth, 2005). This
approach does not only combine identical sub-trees,
but recognizes similar patterns within the XML tree,
and therefore allows a higher degree of compression.
The approach presented in this paper follows the
same idea. But instead of combining similar struc-
tures bottom-up, our approach searches within a giv-
en window the most promising pair to be combined
while following one of three possible clustering
strategies. Both approaches allow querying of com-
pressed data and can be applied to infinite XML data
streams if the search for similar substructures is re-
stricted to a given window size.
The approach in (Ferragina et al., 2006) does not
belong to any of the three categories. It is based on
BurrowsWheeler BlockSorting (Burrows and Whee-
ler, 1994), i.e., the XML data is rearranged in such a
way that compression techniques such as gzip
achieve higher compression ratios. This approach is
not applicable to data streams, but allows querying
the compressed data if it is enriched with additional
index information.
Different from all other approaches, CluX uses
clustering for grammar-based XML compression.
In contrast to the RePAIR algorithm presented in
(Larsson and Moffat, 2000) for strings and used in
(Claude and Navarro, 2007) to compress the adja-
cency lists of graphs, we do not only compress lists
of symbols (i.e., one-dimensional structures) with
the help of parameter-less grammars, but instead
compress binary trees (i.e., two-dimensional struc-
tures) with the help of a parameterized grammar.
6 SUMMARY AND
CONCLUSIONS
We have shown how CluX, a clustering-based com-
pression approach for XML trees, uses clustering for
determining the most promising similar sub-trees
and shares them by using a single pattern. As an
XML file compressor, CluX compresses better than
the XML compressor XMill or than generic com-
pressors like gzip or BZip2. CluX compression can
be applied to infinite data streams – and in contrast
to XMill and gzip or BZip2, path queries can be eva-
luated directly on the compressed representation,
i.e., without prior decompression. By sharing, CluX
decreases the number of edges down to less than
10% of an original XML document tree. This allows
not only a more space saving in-memory representa-
CLUX - Clustering XML Sub-trees
149

tion of an XML document tree than standard tree re-
presentations or DOM, but also is promising for
faster bottom-up query evaluation. Therefore, we re-
gard CluX to be a useful compressor for SEPA or
MS Office documents, product catalogs and other
XML data, whenever the data volume is a bottleneck
in enterprise information systems.
REFERENCES
J. Adiego, G. Navarro, P. de la Fuente: Lempel-Ziv Com-
pression of Structured Text. Data Compression Con-
ference 2004
A. Arion, A. Bonifati, I. Manolescu, A. Pugliese. XQueC:
A Query-Conscious Compressed XML Database, to
appear in ACM Transactions on Internet Technology.
D. Arroyuelo, F. Claude, S. Maneth, V. Mäkinen, G. Na-
varro, K. Nguyen, J. Siren, N. Välimäki, 2010: Fast
In-Memory XPath Search over Compressed Text and
Tree Indexes. ICDE 2010.
R. J. Bayardo, D. Gruhl, V. Josifovski, and J. Myllymaki.,
2004. An evaluation of binary xml encoding optimiza-
tions for fast stream based XML processing. In Proc.
of the 13th international conference on World Wide
Web.
S. Böttcher, R. Hartel, Ch. Heinzemann: BSBC: Com-
pressing XML streams with DAG + BSBC. In:
WEBIST 2008, Funchal, Portugal, 2008.
S. Böttcher, R. Hartel, Ch. Messinger: XML Stream Data
Reduction by Shared KST Signatures. HICSS 2009
S. Böttcher, R. Steinmetz, N. Klein, 2007. XML Index
Compression by DTD Subtraction. International Con-
ference on Enterprise Information Systems (ICEIS).
P. Buneman, M. Grohe, Ch. Koch, 2003. Path Queries on
Compressed XML. VLDB.
M. Burrows and D. Wheeler, 1994. A block sorting loss-
less data compression algorithm. Technical Report
124, Digital Equipment Corporation.
G. Busatto, M. Lohrey, and S. Maneth, 2005. Efficient
Memory Representation of XML Dokuments, DBPL.
J. Cheney, 2001. Compressing XML with multiplexed hie-
rarchical models. In Proceedings of the 2001 IEEE
Data Compression Conference (DCC 2001).
J. Cheng, W. Ng: XQzip, 2004. Querying Compressed
XML Using Structural Indexing. EDBT.
F. Claude and G. Navarro, 2007: A Fast and Compact
Web Graph Representation. Proc. 14th International
Symposium on String Processing and Information Re-
trieval (SPIRE).
P. Ferragina, F. Luccio, G. Manzini, and S. Muthukrish-
nan, 2006. Compressing and Searching XML Data Via
Two Zips. In Proceedings of the Fifteenth Interna-
tional World Wide Web Conference.
D. K. Fisher and S. Maneth, 2007. Structural Selectivity
Estimation for XML Documents. In Proc of the ICDE.
M. Girardot and N. Sundaresan. Millau, 2000. An Encod-
ing Format for Efficient Representation and Exchange
of XML over the Web. Proceedings of the 9th Interna-
tional WWW Conference.
D. A. Huffman, 1952. A method for the construction of
minimum-redundancy codes. In: Proc. of the I.R.E
.
J. Larsson and A. Moffat, 2000: Off-Line Dictionary-
Based Compression. Procceedings of the IEEE.
H. Liefke and D. Suciu, 2000. XMill: An Efficient Com-
pressor for XML Data, Proc. of ACM SIGMOD.
J. K. Min, M. J. Park, C. W. Chung, 2003. XPRESS: A
Queryable Compression for XML Data. In Proceed-
ings of SIGMOD.
W. Ng, W. Y. Lam, P. T. Wood, M. Levene, 2006: XCQ:
A queryable XML compression system. Knowledge
and Information Systems.
D. Olteanu, H. Meuss, T. Furche, F. Bry, 2002: XPath:
Looking Forward. EDBT Workshops.
A. Schmidt, F. Waas, M. Kersten, M. Carey, I. Manolescu,
and R. Busse, 2002. XMark: A benchmark for XML
data management. Hong Kong, China.
H. Subramanian, P. Shankar: Compressing XML Docu-
ments Using Recursive Finite State Automata. CIAA
2005
P. M. Tolani and J. R. Hartisa, 2002. XGRIND: A query-
friendly XML compressor. In Proc. ICDE.
Ch. Werner, C. Buschmann, Y. Brandt, S. Fischer: Com-
pressing SOAP Messages by using Pushdown Auto-
mata. ICWS 2006
N. Zhang, V. Kacholia, M. T. Özsu, 2004. A Succinct
Physical Storage Scheme for Efficient Evaluation of
Path Queries in XML. ICDE
J. Ziv and A. Lempel: A Universal Algorithm for Sequen-
tial Data Compression, 1977. In IEEE Transactions on
Information Theory, No. 3, Volume 23, 337-343
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
150