IDENTIFICATION OF DISCRETE EVENT SYSTEMS

Implementation Issues and Model Completeness

∗

Matthias Roth

1,2

, Lothar Litz

and Jean-Jacques Lesage

Institute of Automatic Control, University of Kaiserslautern, Germany

LURPA, Ecole Normal Sup

erieur de Cachan, France

Keywords:

Discrete event systems, Identiﬁcation, Implementation.

Abstract:

This paper presents some practical issues for the identiﬁcation of discrete event systems (DES). The considered

class of systems consists of a plant and a controller running is a closed-loop. Special emphasis is given

to a data collection procedure using industrial controllers and its impact on the external DES-behavior of

the considered systems. For models identiﬁed on the basis of observed external DES behavior using the

algorithm from (Klein, 2005) it is shown that under some conditions, the identiﬁed model language simulates

the complete original system language even if only a subset of this language is available for identiﬁcation. This

model characteristic is crucial for many model-based techniques like diagnosis or veriﬁcation. Analyzing the

observed data of a laboratory facility it is shown how it can be decided if the conditions for a complete model

hold for an existing application.

1 INTRODUCTION

Model-based techniques play a key role in many mod-

ern control applications. For systems that can be

modeled as Discrete Event Systems (DES) various

approaches to improve system dependability using

model-based methods have been proposed in the last

two decades. Examples for these methods are diag-

nosis (Sampath et al., 1996) and formal veriﬁcation

with model checking (Machado et al., 2006). A bot-

tleneck for the application of model-based techniques

is the process of model-building which is usually ex-

pensive due to high costs for the necessary specialists.

A promising way to facilitate the use of model-based

methods is to offer efﬁcient identiﬁcation methods in

order to decrease the cost of model-building.

First approaches for the identiﬁcation of DES have

been proposed in the sixties and seventies of the last

century in the ﬁeld of computer science (Biermann

and Feldman, 1972). The identiﬁcation of physical

systems which is a typical interest in many engineer-

ing domains is not the aim of these works. More re-

cent works especially on identiﬁcation of Petri nets

are summarized in (Fanti and Seatzu, 2008). In

the last years two main directions of constructing a

∗

This works was partially supported by a grant from

egion

Ile-de-France

Petri net from samples of its language have been fol-

lowed: In the ﬁrst class of approaches speciﬁc rules

about interdependencies of observed events are used

to identify a Petri net on the basis of observed ﬁring

and marking sequences (Meda-Campana and Lopez-

Mellado, 2005). The second class of approaches uses

optimization techniques like integer programming to

derive a Petri net structure according to given con-

straints (Giua and Seatzu, 2005), (Dotoli et al., 2006).

The main obstacle for the application of these

methods to real world systems is their relatively high

degree of abstraction. The work is usually not focused

on questions like how to represent data that can be

captured from a real system and how to cope with

inadequacies inherent to the data collection process.

In (Dotoli et al., 2006) a case study shows that there

is a considerable potential of identiﬁcation methods

to obtain meaningful DES models of physical sys-

tems. Since the identiﬁcation data base in this work

has been obtained by simulating a three tank system,

important issues of working with data captured from

a real system have not been addressed.

In (Klein et al., 2005) an algorithm for the iden-

tiﬁcation of closed-loop DES is presented. The algo-

rithm has been designed to work with data obtained

from real systems and yields a monolithic automaton.

In this paper some implementation issues concerning

the application of this algorithm to a real system are

Roth M., Litz L. and Lesage J. (2010).

IDENTIFICATION OF DISCRETE EVENT SYSTEMS - Implementation Issues and Model Completeness.

In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 73-80

DOI: 10.5220/0002879900730080

 SciTePress

presented. In section 2 the class of closed-loop DES

is presented and it is outlined that this system class

is an appropriate modeling formalism for many in-

dustrial systems. Section 3 summarizes some prac-

tical implications of the data collection procedure and

deﬁnes an appropriate data format for the identiﬁca-

tion algorithm. The identiﬁcation algorithm is com-

pactly presented in section 4. An important property

of models identiﬁed with this algorithm is proofed in

this section: Under some well-deﬁned conditions con-

cerning the observed system language, the identiﬁed

model is able to simulate the complete original sys-

tem language of arbitrary length

. In section 5 the

data collection procedure and the identiﬁcation algo-

rithm are applied to a laboratory facility in order to

show the relevance of the approach for real systems.

It is shown how it can be decided of if the precondi-

tions presented in the former section hold only using

measured system data.

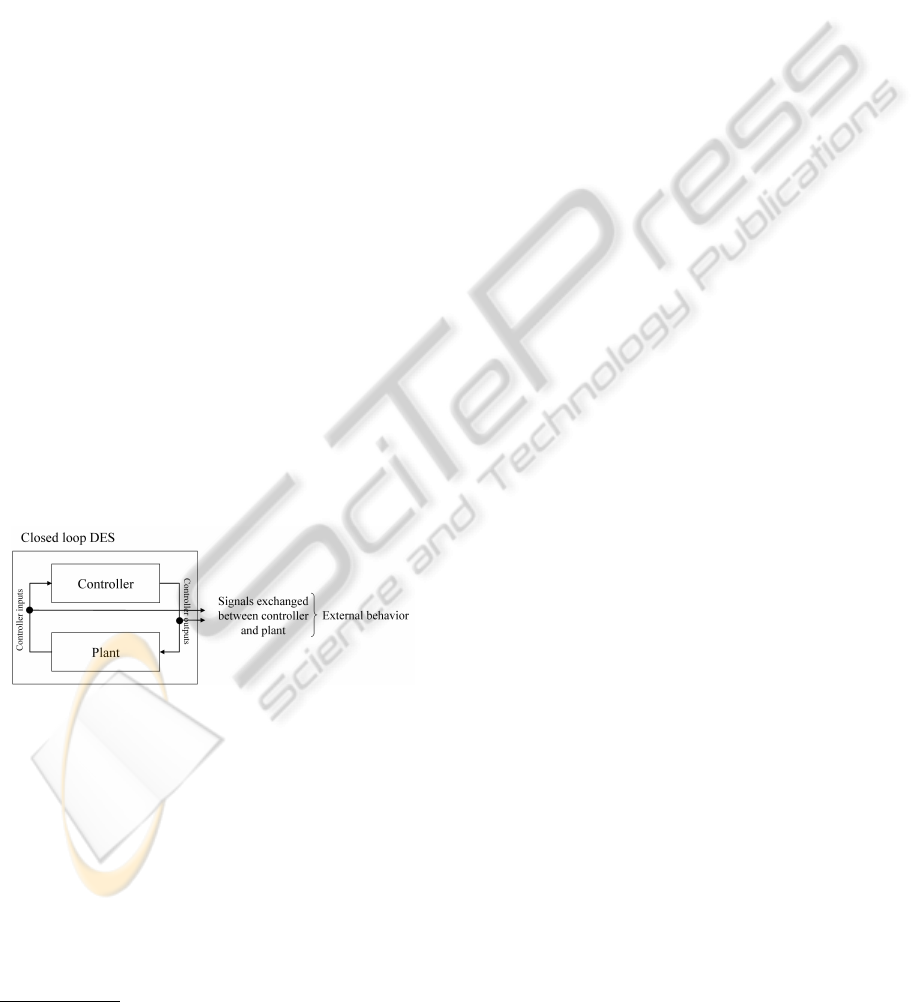
2 CLOSED-LOOP DES

A typical conﬁguration of industrial systems is a

closed-loop of controller and plant. In the plant, a

set of sensors measures certain process values and de-

livers them to the controller using the controller in-

puts. The controller executes a control algorithm and

determines appropriate actuator settings for the plant.

Commands to actuators in the plant are transfered via

controller output signals. Figure 1 shows this princi-

ple.

Figure 1: Closed-loop Discrete Event system.

The external behavior of such systems can be ob-

tained by an analysis of the signals exchanged be-

tween controller and plant. In the considered class

of systems these signals are binary. From an exter-

nal point of view, a signal changes its value asyn-

chronously which can be considered as the occurrence

of an event. The closed-loop system can be charac-

terized as non-deterministic since it consists of the

combination of a deterministic subsystem (controller)

and a non-deterministic subsystem (plant). Since the

closed-loop system does not have any inputs, it must

Language L

simulates language L

if L

⊇ L

holds

be considered as an event generator (note that the

controller inputs also belong to the external behav-

ior of the closed-loop DES). This system character-

istic shows that the application of test functions for

identiﬁcation purposes like it is often done in contin-

uous systems is not possible for industrial closed-loop

DES. Only passive identiﬁcation approaches work-

ing on observed system evolutions are suitable for the

considered system class.

The aim of identiﬁcation is to deliver a model to

reproduce the external behavior of the closed-loop

system. Hence, it is necessary to capture the signals

exchanged between controller and plant in order to get

samples of the external system behavior. In case of

existing industrial facilities this process must be non-

invasive to avoid disturbances of the process. In the

next section, a method to capture these signals in an

efﬁcient way is presented.

3 DATA COLLECTION

3.1 Technical Implementation

The implementation of a data collection procedure for

closed-loop DES necessitates capturing the signals

exchanged between plant and controller. The most ac-

curate approach to get the according signal values is

to connect the wires between sensors or actuators and

the controller with a special data collection hardware

like described in (de Smet et al., 2001). Although

such an approach is possible within a laboratory en-

vironment, for existing industrial facilities the neces-

sary cabling effort would be too important. Since one

of the main reasons to use identiﬁcation methods is to

save costs, the effort to apply the method must not ex-

ceed the costs of manually model building. A slightly

less accurate data collection approach that can be im-

plemented with less effort is to collect the signals after

they have been captured by the controller.

Figure 2 shows the functional principle of a pro-

grammable logic controller (PLC) which is a widely

used class of controllers in industry. The controller

cyclically performs the steps ’input reading’ where it

reads the signals from the sensors, ’program execu-

tion’ to determine new output values for the actua-

tors, and ’output writing’ where the newly determined

commands are sent to the plant actuators. Modern

PLCs are equipped with a communication processor

which makes it possible to send the values of the in-

put and output signals to a standard PC where they can

be stored in a data base. The implementation of such

a connection is relatively easy (it is mainly a software

problem) and does not require any special hardware.

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

Figure 2: PLC cycle and data collection.

As implementation of the data link between con-

troller and identiﬁcation data base, a UDP (User Data-

gram Protocol) connection is used. At the end of the

’program execution’ phase, the communication pro-

cessor of the controller sends a UDP-datagram which

is received by the PC with the identiﬁcation data

base. In order to validate that this connection is fast

enough to be used for data collection, tests have been

performed using a Siemens PLC (CPU 315-2 DP)

equipped with a program leading to a PLC-cycle time

of 25 to 30 ms. The PLC as a communication proces-

sor (CP 343-1 IT) which sends the data to a standard

PC (identiﬁcation data base). Figure 3 shows that the

time between the reception of two packages alters be-

tween 25 ms and 30 ms according to the slightly vary-

ing PLC-cycle. It could also be observed that no data

packets got lost during the transmission. This shows

that the UDP connection is adapted for our purposes.

Figure 3: Validation of the UDP connection.

When the signal values are sent to the identiﬁca-

tion data base, they are grouped in the controller I/O

(input/output) vector deﬁned as follows:

Deﬁnition 1 (Controller I/O vector). Given r different

controller inputs I

, ..., I

and s different controller

outputs O

, ..., O

, the controller I/O vector u = (IO

..., IO

) with m = r + s is given by IO

= I

∀ i =

1,..,r and IO

r+1

= O

∀ i = 1,..,s. m = |u| denotes

the length of the vector (number of controller I/Os).

The controller I/O vectors which are sent to the

identiﬁcation data base differ slightly from the real

values of the signals. Three scenarios are considered

to describe how the controller I/O vector captured in

the data base is affected by the data collection process

at the end of the ’program execution’ step in the PLC.

Figure 4 shows the evolution of two controller in-

puts (sensor values) in the plant. It can be seen that

the two signals change their values at different times

since the according sensors are not triggered simulta-

neously. In the middle of the ﬁgure, the PLC-cycle is

shown over time. The dotted line indicates that the

input values of the plant are read by the PLC dur-

ing the step ’input reading’. After the program exe-

cution phase, the input values are sent to the identiﬁ-

cation data base. The evolution of the data received

in the data base (the sampled data) is shown below

the PLC cycle. Since the real values of the two inputs

have been captured simultaneously during the ’input

reading’ phase they also change their value simulta-

neously in the identiﬁcation data base. As a conse-

quence for the identiﬁcation algorithm it is important

to use an appropriate deﬁnition of the notion event.

Since in DES theory events cannot occur simultane-

ously it is not possible to deﬁne the change in value

of one signal as an event like it would probably be

the most intuitive way. Instead we use the following

deﬁnition:

Deﬁnition 2 (Event). The appearance of an event

leads to a new I/O vector u( j) with u( j) 6= u( j − 1).

Only I/O vectors generated by events are stored in the

data base.

As a consequence of the this deﬁnition, two suc-

cessive I/O vectors u( j) and u( j + 1) always differ in

at least one (but possibly more than one) I/O value.

In ﬁgure 5 a scenario with a controller input and

a controller output is shown. In the example it is

assumed that there is a logical condition in the con-

trol algorithm relating these two signals: if the input

changes its value, the controller changes the value of

the output as a consequence. It can be seen that the

cause (change in value of the input) and the accord-

ing effect (change in value of the output) are sent si-

multaneously to the data base. Hence, in the data

base cause and effect cannot not directly be seen. Ad-

ditionally, the ﬁgure shows that using the described

data collection procedure it is possible to receive I/O

vectors in the data base before the according output

values are valid for the plant. The output values are

sent to the plant during the step ’output writing’ which

takes place after the transfer of the I/O vector.

The third scenario in ﬁgure 6 shows the case of an

actuator inﬂuencing a sensor in the plant. When the

according output is set in the controller it is transfered

to the data base and with a short delay written to the

the plant. The actuator controlled by the output can

only then start inﬂuencing the sensor connected with

IDENTIFICATION OF DISCRETE EVENT SYSTEMS - Implementation Issues and Model Completeness

Figure 4: Sampling scenario 1.

Figure 5: Sampling scenario 2.

input 1. Hence, in this case cause and effect cannot

be captured simultaneously since the change in value

of input 1 occurs some time after the vector with the

change in value of output 1 has been sent to the iden-

tiﬁcation data base. The delay of cause and effect is

often not considered in manually built models like in

(Sampath et al., 1996). A second issue of the data

collection process can also be seen in the ﬁgure: al-

though input 1 and output 1 change their value rela-

tively fast one after the other (faster than the duration

of a PLC-cycle), it can take up to one PLC cycle until

this change in value is sent to the identiﬁcation data

base.

Figure 6: Sampling scenario 3.

The three scenarios show that the selected data

collection procedure introduces some inadequacies

that will also be part of the identiﬁed model. It is

thus important to clearly indicate when the data has

been captured in the PLC-cycle to precisely describe

the data in the identiﬁcation data base.

3.2 Deﬁnition of the Observed

Language

For identiﬁcation, the captured system data can be

interpreted as the language of the considered closed-

loop DES. The identiﬁcation is based on the observa-

tion of I/O vector sequences during l

different system

evolutions:

Deﬁnition 3 (I/O vector sequence). If during the h-th

system evolution l

I/O vectors u

have been ob-

served, the sequence is denoted as σ(h) = (u

(1),

(2), . . . , u

)).

The term ’system evolution’ refers to a system run

of a certain length. In manufacturing systems such an

evolution can be a production cycle. Based on the I/O

vector sequences it is possible to deﬁne the observed

word set (I/O vector sequences of a given length) and

the observed language:

Deﬁnition 4 (Observed word set and language).

The observed words of length q captured during p

different system evolutions are denoted as

Obs

[

i=1

(

−q+1

[

j=1

( j),u

( j + 1), . . . , u

( j + q − 1))).

With the observed word set we can deﬁne the observed

language of length n of the system starting from any

reachable state as

Obs

[

i=1

Obs

In most practical applications the observed sys-

tem language is only a subset of the possible system

language L

Orig

. The longer a closed loop system is

observed, the more likely the cardinality of L

Obs

con-

verges to a certain value. If new system evolutions do

not lead to new words in L

Obs

, the system language

Orig

can reasonably be considered as completely ob-

served (L

Obs

≈ L

Orig

). Figure 7 shows typical evolu-

tions of the observed language in case of convergence

and in case of continued growth. In practical applica-

tion it is often the case that L

Obs

converges for smaller

values of n but still grows for larger values. As an

example consider the case when each possible single

system output has been observed (L

Obs

converges) but

there still occur new combinations (sequences) of al-

ready known single system outputs (L

n>1

Obs

continues to

grow).

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

Figure 7: Principle of a converging language.

4 IDENTIFICATION

The aim of identiﬁcation is to build a model that ap-

proximates the original system language L

Orig

. In

(Klein, 2005) a non-deterministic autonomous au-

tomaton with output is chosen as an appropriate

model to reproduce the observed language of closed-

loop discrete event systems:

Deﬁnition 5 (Non Deterministic Autonomous Au-

tomaton with Output). NDAAO = (X,Ω,r, λ, x

)

with X ﬁnite set of states, Ω output alphabet, r : X →

non-deterministic transition relation, λ : X → Ω

output function and x

the initial state.

If the output alphabet Ω consists of the captured

I/O vectors it is possible to approximate the observed

language L

Obs

by performing state trajectories in the

automaton:

Deﬁnition 6 (Words and Language of the NDAAO).

The set of words of length n generated from a state

x(i) is deﬁned as:

n=1

x(i)

= {w ∈ Ω

: w = λ(x(i))}

and

n>1

x(i)

= {w ∈ Ω

: w = (λ(x(i)),λ(x(i + 1)),

...,λ(x(i + n − 1))) : x( j + 1) ∈ r(x( j))

∀i ≤ j ≤ i + n − 2}

The language of length n generated by the NDAAO is

given by

Ident

[

i=1

[

x∈X

In (Klein, 2005) an algorithm to identify an

NDAAO based on an observed language is given.

The algorithm delivers a model that is k + 1-complete

which means that L

k+1

Ident

= L

k+1

Obs

(proof can be found in

(Klein, 2005)). This property excludes that the identi-

ﬁed model contains any non-observed word of length

k + 1. This makes the model suitable for fault de-

tection purposes (Roth et al., 2009). It is also the

basis for the completeness of the model which will

be shown at the end of the section. The algorithm

uses words of the parametric length k to construct the

NDAAO. The observed I/O vector sequences in the

data base have to be modiﬁed according to the fol-

lowing equation. It duplicates the ﬁrst vector of each

sequence k − 1 times:

(i) =

(

(1) for 1 ≤ i ≤ k

(i − k + 1) for k < i ≤ k + |σ

| − 1

(1)

On the basis of Σ

= {σ

,...,σ

} we determine

the observed word sets of length k and k + 1 for the

identiﬁcation:

Obs,Σ

[

∈Σ

(

|σ

|−k+1

[

i=1

(i),u

(i+1), ...,u

(i+k −1)))

(2)

k+1

Obs,Σ

[

∈Σ

(

|σ

|−k

[

i=1

(i),u

(i + 1), . . . , u

(i + k)))

The identiﬁcation procedure is given in algo-

rithm 1. It is a condensed version of the algorithm

given in (Klein, 2005). For the algorithm, we deﬁne

an operator w[a..b] to deliver the substring from po-

sition a to position b in word w. In the ﬁrst step,

for each word of length k a state is created. If two

words of length k have been observed successively,

they build a word of length k + 1. Hence, the states

representing the two words of length k are connected

in step 2 of the algorithm. In step 3, the output func-

tion of each state is redeﬁned. The new state output

is the I/O vector at the end of the word of length k

representing the state output so far. In the last step,

states with equal output and equal following states are

merged. A detailed description of this procedure is

given in (Klein, 2005).

An interesting characteristic of a model identiﬁed

with algorithm 1 is that under certain conditions the

identiﬁed language does not only reproduce the sys-

tem behavior observed so far (L

Ident

⊇ L

Obs

) but the

complete original system language (L

Ident

⊇ L

Orig

This property (which is not proved in (Klein, 2005))

is very important for many model-based techniques

relying on a complete system description. In the fol-

lowing, the necessary conditions to proof the charac-

teristic are given. The ﬁrst step is to show that each

state trajectory producing a word of length k ends in

the same state. In the following, w

denotes a word of

length k.

Lemma 1. In an NDAAO identiﬁed with parameter k

each state trajectory λ(x(i), . . . , x(i + k − 1)) = w

∈

Ident

|x( j + 1) ∈ r(x( j))∀i ≤ j < i + k − 1 ends in the

same state.

IDENTIFICATION OF DISCRETE EVENT SYSTEMS - Implementation Issues and Model Completeness

Algorithm 1: Identiﬁcation algorithm.

Require: Parameter k, observed word sets W

Obs,Σ

and W

k+1

Obs,Σ

1: X = {x|∀w ∈ W

Obs,Σ

: ∃!x|λ(x) := w,r(x) := {}}

2: ∀(x,x

,w) ∈ X ×X ×W

k+1

Obs,Σ

|λ(x) = w[1,. . . , k]∧

λ(x

) = w[2,.., k + 1] : r(x) := r(x) ∪ x

3: x

= x ∈ X|λ(x) = w

and w

[i] = σ

(1)∀1 ≤ i ≤ k

4: ∀x ∈ X : λ(x) := λ(x)[|λ(x)|]

5: Merge x

∈ X with λ(x

) = λ(x

) and r(x

) =

r(x

)

We deﬁne a function

λ(x) delivering w

used in

step 1 for each state of the algorithm. It represents

the state output before it has been replaced by the I/O

vector at the end of the word of length k representing

the state output until step 3.

Proof of lemma 1. From equations 1 and 2 it fol-

lows that ∀w

∈ L

Obs

∃v

,...,v

∈ W

Obs,Σ

[k] =

[1],v

[k − 1 ...k] = w

[1...2],...,v

[1...k] =

[1...k]. From steps 1 and 2 of algorithm 1 it fol-

lows that states representing v

,...,v

are connected

since ∀v

∃w

k+1

∈ W

k+1

Obs,Σ

k+1

= v

[1...k]v

[k].

Since step 1 assures that ∀w

∈ L

Ident

∃!x|

λ(x) = w

it follows that each state trajectory with

λ(x(i),...,x(i + k − 1)) = w

∈ L

Ident

|x( j + 1) ∈

r(x( j))∀i ≤ j < i + k − 1 ends in the same state.

In the next theorem, it is stated that the identiﬁed

language simulates the original system language of

arbitrary length if L

k+1

Orig

= L

k+1

Obs

holds for a given value

of the identiﬁcation parameter k.

Theorem 1. If L

k+1

Orig

= L

k+1

Obs

, then L

k+n

Ident

⊇ L

k+n

Orig

for

an NDAAO identiﬁed with parameter k.

Proof of theorem 1. L

k+1

Ident

⊇ L

k+1

Orig

since the iden-

tiﬁed NDAAO is k + 1 complete. For k + 2 it

holds: ∀w

k+2

∈ L

k+2

Orig

∃a

= d

= s

k+2

∈ L

k+1

Orig

= L

k+1

Obs

. Each state tra-

jectory producing a

ends in the same state x

(lemma

1). In step 2 of the algorithm, this state is connected

with x

λ(x

) = u

. Each state trajectory producing

ends in the same state x

which gets connected

to x

λ(x

) = f

. Since there is a trajectory lead-

ing to state x

and x

, x

and x

are in one trajec-

tory, it follows that ∀w

k+2

∈ L

k+2

Orig

there exists a tra-

jectory of states producing this word. For larger val-

ues than k + 2 ∀w

k+n

∈ L

k+n

Orig

there is always an ap-

propriate decomposition into already observed sub-

strings of L

k+1

Orig

= L

k+1

Obs

to ﬁnd a trajectory of con-

nected states like presented above. Hence, it follows

that L

k+n

Ident

⊇ L

k+n

Orig

if L

k+1

Orig

= L

k+1

Obs

holds.

Theorem 1 shows that it is crucial to state L

k+1

Orig

k+1

Obs

for a precise k in order to deliver a model which

is able to simulate the complete original system be-

havior. In section 3.2 it is shown how it can be de-

cided if L

k+1

Orig

= L

k+1

Obs

holds for a given value of k.

5 APPLICATION

In order to show that the identiﬁcation algorithm of

section 4 is capable of delivering a model of existing

systems that can be interpreted as closed-loop DES,

one of the case studies we have treated will be pre-

sented in this section. The system depicted in ﬁgure 8

has 30 digital I/Os and is controlled by a Siemens

PLC equipped with a communication processor. The

system treats work pieces stored in the left most part

of the facility. Each work piece is successively treated

by the three tools. For identiﬁcation a system evolu-

tion is deﬁned as the run of two work pieces through

the machine. Hence, there are at most two work

pieces treated concurrently in the whole system.

Figure 8: Laboratory facility.

50 system evolutions (treating 50 times two work

pieces) have been performed and the according data

has been collected using the procedure described in

section 3. The observed word sets of different length

are shown in ﬁgure 9. It can be seen that for small

values of n like n = 2 or n = 3 the according ob-

served word set and thus the observed language con-

verges to a stable level which implies that the ob-

served language converges to the original system lan-

guage (L

n=3

Obs

≈ L

n=3

Orig

). Although for L

Obs

there is a

new word observed in one of the last evolutions, it

can still reasonably be considered as completely ob-

served. Hence, the precondition of theorem 1 is ful-

ﬁlled. Since L

n=3

Obs

≈ L

n=3

Orig

, it is possible to identify an

NDAAO with k + 1 = n = 3 (→ k = 2) to simulate the

original system behavior.

For the identiﬁcation of an NDAAO a software

tool has been developed. Like depicted in ﬁgure 10,

it takes the data base consisting of the observed sys-

tem evolutions and the identiﬁcation parameter k as

input and applies algorithm 1. The software allows

an analysis of the model structure (number of states,

number of transitions etc.) and a behavioral analysis

(see below). The identiﬁed model can be exported to

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

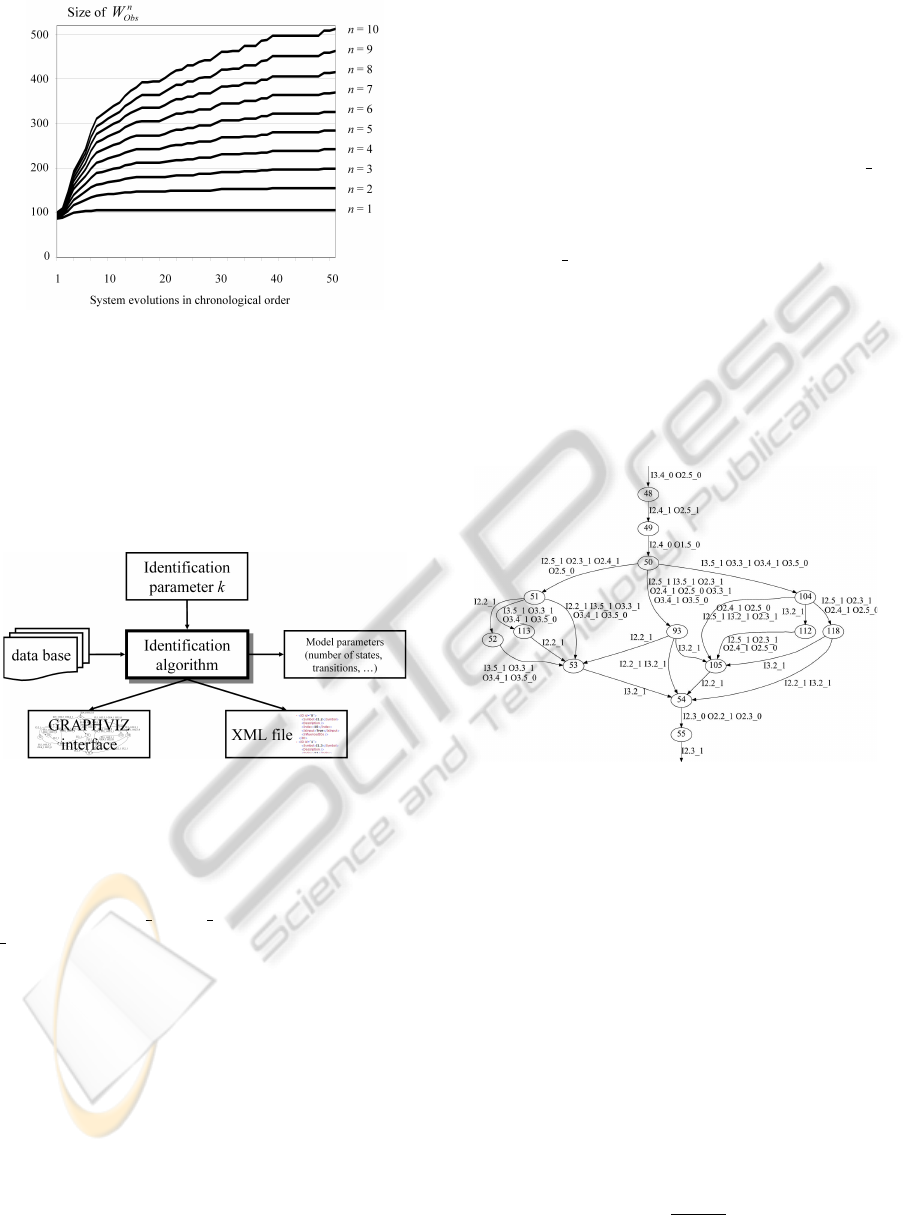
Figure 9: Observed word set for the laboratory system.

an XML-ﬁle to use it in other tools such as diagnosis

software (Roth et al., 2009). To visualize the resulting

automaton, an interface to GRAPHVIZ is provided.

The identiﬁcation of the NDAAO with k = 2 on the

basis of 50 system evolutions took 170 ms on a stan-

dard PC with a 1.79 Ghz CPU and 1.96 GB RAM. The

identiﬁed model has 121 states and 162 transitions.

Figure 10: Features of the implemented software.

A part of the identiﬁed NDAAO can be seen in

ﬁgure 11. Due to space limitations, instead of giv-

ing the complete I/O vector in each state output, only

I/Os changing their value from one state to another

are given (e.g. I2.4 1 O2.5 1 to indicate a rising edge

( 1) of controller Input I2.4 and a rising edge of con-

troller Output O2.5 from state 48 to state 49). Several

examples for the different I/O vector sampling scenar-

ios presented in section 3.1 can be seen in the model.

For the scenario with two controller inputs changing

their value synchronously due to the data collection

process (ﬁgure 4), the transition between states 93 and

54 is an example. Both inputs I2.2 and I3.2 change

their value when taking this transition. The transi-

tion from state 48 to 49 is an example for the sec-

ond sampling scenario (ﬁgure 5) where the change in

value of an input triggers the change in value of an

output. This transition represents the situation when

the second work arrives at the entrance of the sec-

ond station (position sensor connected to I2.4 changes

its value) and the conveyor of this station is started

(controller output O2.5 is set to 1). Both changes in

value appear at one transition due to the data collec-

tion process as explained in section 3.1. An example

for the third scenario form section 3.1 (ﬁgure 6) can

be seen in the state trajectory x

→ x

. From

state 48 to state 49 the conveyor is started (O2.5 1)

to transport the work piece away from the entrance

position (I2.5). Since it takes at least until the next

PLC cycle to transport the work piece away from the

sensor (I2.5 0 for the falling edge) cause and effect

cannot be seen at once but at some successive transi-

tions. The non-deterministic nature of the identiﬁed

NDAAO can also be seen in ﬁgure 11: there are sev-

eral ways to go from state 50 to state 55. Being in state

50 the choice of the trajectory is not determined but

taken at random like in the closed-loop DES where

unpredictable physical conditions in the plant lead to

non-deterministic behavior.

Figure 11: Part of the identiﬁed NDAAO.

One of the important characteristics of the identi-

ﬁed model is its capability to simulate the complete

original system language (theorem 1). Even if only

a subset of possible I/O vector sequences connecting

the closed-loop system states represented by NDAAO

states 50 and 55 has been observed, the model con-

tains each possible trajectory that can occur when go-

ing from one state to the other as long as no new

word of length k + 1 is produced. If L

k+1

Orig

= L

k+1

Obs

the model is capable of exhibiting words of length

k + n although these words have not been seen be-

fore. This capability comes at cost of also exhibit-

ing words that have not and probably will not be ob-

served (w

k+n

/∈ L

k+n

Orig

). To get some information of

the amount of words which are created without hav-

ing been observed, the coefﬁcient

Ident

Obs

is a useful indicator. The presentation of the coefﬁ-

IDENTIFICATION OF DISCRETE EVENT SYSTEMS - Implementation Issues and Model Completeness

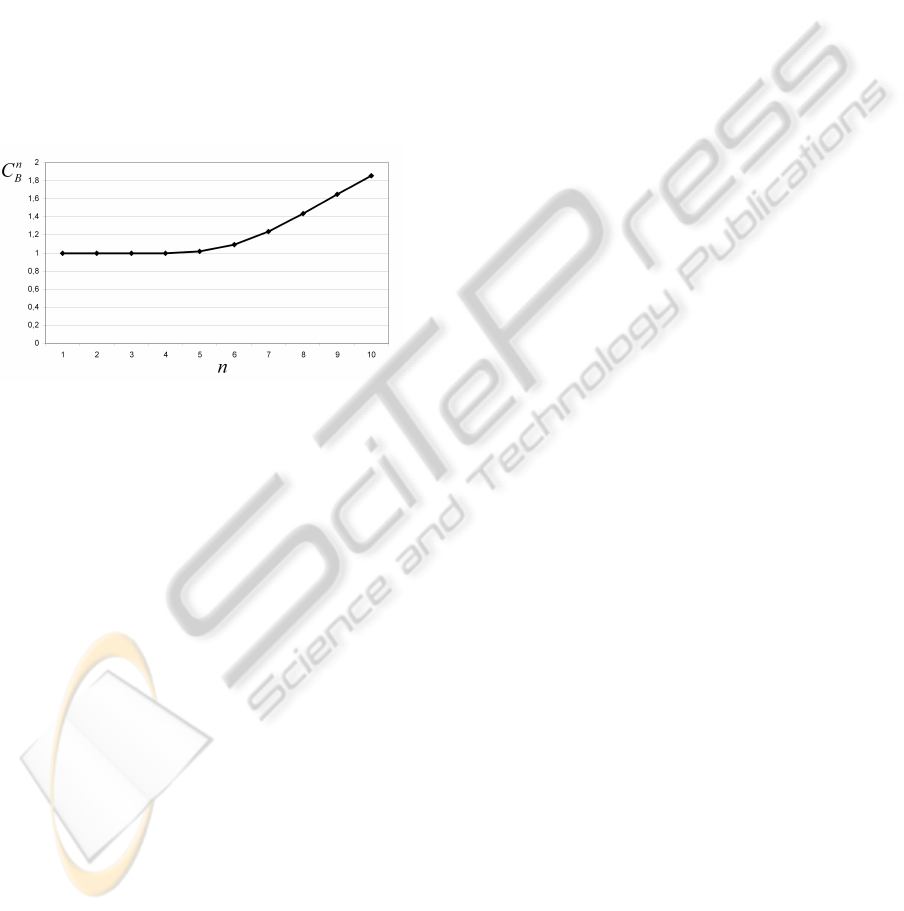
cient in ﬁgure 12 describes the relation between the

identiﬁed and the observed language of an automa-

ton identiﬁed with k = 2. For n = k + 1, the model

strictly creates the observed language L

k+1

Obs

. It can be

seen that for larger values of n the automaton gener-

ates a larger language than L

Obs

. A certain part of the

additionally created words is probably not part of the

original system language which may lead to a need for

speciﬁc precautions in some model based techniques

like diagnosis. However, from theorem 1 it is clear

that each word with length n ≥ k + 1 of the original

language not observed so far is part of the identiﬁed

language. In the case of model based diagnosis for

example, this allows stating that there will be no false

alerts using the identiﬁed automaton as fault-free ref-

erence model (Roth et al., 2009).

Figure 12: Coefﬁcient of identiﬁed and observed language.

6 CONCLUSIONS

In this paper practical implications of identiﬁcation

of closed-loop discrete event systems have been ad-

dressed. It has been shown how the necessary data

can be obtained in the case of industrial closed-loop

systems. For many model-based techniques it is cru-

cial to have a model of the complete system behav-

ior. For the identiﬁcation algorithm of (Klein, 2005) it

has been proved that the identiﬁed automaton is sim-

ulates the original system language of arbitrary length

if some conditions concerning the observed system

language hold.

REFERENCES

Biermann, A. and Feldman, J. (1972). On the synthesis of

ﬁnite-state machines from the sample of their behav-

ior. IEEE transactions on computers, 21:592–597.

de Smet, O., Denis, B., Lesage, J.-J., and Roussel, J.-M.

(2001). Dispositif et procd d’analyse de performances

et d’identiﬁcation comportementale d’un systme in-

dustriel en tant qu’automate vnements discrets et ﬁ-

nis. Technical report, French Patent 01 110 933.

Dotoli, M., Fanti, M. P., and Mangini, A. M. (2006). On-

line identiﬁcation of discrete event systems: a case

study. In 2006 IEEE international conference on au-

tomation science and engineering, pages 405–410.

Fanti, M. P. and Seatzu, C. (2008). Fault diagnosis and iden-

tiﬁcation of discrete event systems using petri nets.

In Proceedings of the 9th International Workshop on

Discrete Event Systems, Gtebor, Sweden, pages 432–

435.

Giua, A. and Seatzu, C. (2005). Identiﬁcation of free-

labeled petri nets via integer programming. Proceed-

ings of the 44th IEEE Conference on Decision and

Control, and the European Control Conference 2005

Seville, Spain, December 12-15, 2005, pages 7639–

7644.

Klein, S. (2005). Identiﬁcation of Discrete Event Systems

for Fault Detection Purposes. Shaker Verlag.

Klein, S., Litz, L., and Lesage, J.-J. (2005). Fault detec-

tion of discrete event systems using an identiﬁcation

approach. In Proceedings of the 16th IFAC World

Congress, pages CDROM paper n02643, 6 pages.

Machado, J., Denis, B., and Lesage, J. J. (2006). A generic

approach to build plant models for DES veriﬁcation

purposes. In Proceedings of the 8th international

workshop on discrete event systems, pages 407–412.

Meda-Campana, M. and Lopez-Mellado (2005). Identiﬁca-

tion of concurrent discrete event systems using petri

nets. 2005 IMACS: Mathematical Computer, Mod-

elling and Simulation Conference.

Roth, M., Lesage, J.-J., and Litz, L. (2009). An FDI

method for manufacturing systems based on an iden-

tiﬁed model. In Proceedings of the 13th IFAC Sympo-

sium on Information Control Problems in Manufactur-

ing, INCOM’09, pages 1389 – 1394, Moscow, Russia.

IFAC.

Sampath, M., Sengupta, R., Lafortune, S., Sinnamohideen,

K., and Teneketzis, D. (1996). Failure diagnosis using

discrete-event models. IEEE transactions on control

systems technology, 4(2):105–124.

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics