
POSITION ESTIMATION OF MOBILE ROBOTS CONSIDERING
CHARACTERISTIC TERRAIN PROPERTIES
Michael Brunner, Dirk Schulz
Department of Unmanned Systems, Fraunhofer-Institute FKIE, Wachtberg, Germany
Armin B. Cremers
Department of Computer Science, University of Bonn, Bonn, Germany
Keywords:
Mobile robots, Position estimation, Terrain classification, Machine learning.
Abstract:
Due to the varying terrain conditions in outdoor scenarios the kinematics of mobile robots is much more
complex compared to indoor environments. In this paper we present an approach to predict future positions of
mobile robots which considers the current terrain. Our approach uses Gaussian process regression (GPR) mod-
els to estimate future robot positions. An unscented Kalman filter (UKF) is used to project the uncertainties
of the GPR estimates into the position space. The approach utilizes optimized terrain models for estimation.
To decide which model to apply, a terrain classification is implemented using Gaussian process classification
(GPC) models. The transitions between terrains are modeled by a 2-step Bayesian filter (BF). This allows us
to assign different probabilities to distinct terrain sequences, while taking the properties of the classifier into
account and coping with false classifications. Experiments showed the approach to produce better estimates
than approaches considering only a single terrain model and to be competitive to other dynamic approaches.
1 INTRODUCTION
The kinematics of mobile robots in outdoor scenarios
is much more complex than in indoor environments
due to the varying terrain conditions. Therefore, truly
reliable velocity controls for robots which are able to
drive up to 4 m/s or even faster (e.g. Figure 1) are hard
to design. The drivability is primarily determined by
the terrain conditions. Thus, we developed a machine
learning system which predicts the future positions of
mobile robots using optimized terrain models.
In this paper we present a Gaussian processes
(GPs) based method for estimating the positions of
a mobile robot. Our approach considers the differ-
ent terrain conditions to improve prediction quality.
Gaussian process regression (GPR) models are uti-
lized to estimate the translational and rotational ve-
locities of the robot. These estimated velocities are
transferred into the position space using an unscented
Kalman filter (UKF). By projecting the uncertainty
values of the GPR estimates onto the positions, the
UKF enables us to also capitalize the GPR uncertain-
ties. To distinguish the different terrains the robot is
traversing, we classify the spectrums of vertical accel-
erations using Gaussian process classification (GPC).
The transitions between terrains are modeled by a 2-
step Bayesian filter (BF). This allows us to assign dif-
ferent probabilities to distinct terrain sequences, as we
incorporate the properties of the classifier.
The remainder of this paper is organized as fol-
lows: Related work is presented in Section 2. In Sec-
tion 3 we explain GPs. In Section 4 we describe our
dynamic approach. Experiments are shown in Sec-
tion 5. We conclude in Section 6.
2 RELATED WORK
Several works study Gaussian processes (GPs)
and their application to machine learning prob-
lems. A detailed view is provided by Rasmussen
and Williams (Rasmussen and Williams, 2005).
Other works are Williams (Williams, 2002), and
MacKay (MacKay, 1998).
There is a lot of research on prediction of po-
sitions or trajectories of mobile robots. Many dif-
ferent systems are proposed, like a stereo-vision ap-
proach (Agrawal and Konolige, 2006), probability
5
Brunner M., Schulz D. and B. Cremers A. (2010).
POSITION ESTIMATION OF MOBILE ROBOTS CONSIDERING CHARACTERISTIC TERRAIN PROPERTIES.
In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 5-14
DOI: 10.5220/0002880200050014
Copyright
c
SciTePress

Figure 1: The experimental Longcross platform Suworow.
networks (Burgard et al., 1996) or an approach us-
ing a particle filter combined with a Monte-Carlo
method (Thrun et al., 2000). In (Seyr et al., 2005) arti-
ficial neural networks (ANN) are employed to build a
model predictive controller (MPC). The current pre-
diction error is considered to improve the quality of
the velocity estimations. Another least-square sup-
port vector machine (LS-SVM) based controller ad-
justs it’s data model iteratively by removing the least
important data point from the model when adding a
new point (Li-Juan et al., 2007).
Similar to the work presented here, GPs are used
by Girard et al. (Girard et al., 2003) to make predic-
tions several time steps ahead. The uncertainty of the
previous step is integrated in the regression to track
the increasing uncertainty of the estimation. Hence,
the uncertainty value of the GP is the accumulated
uncertainty of the previous time series. In contrast,
we are able to relate the Gaussian uncertainties by us-
ing an UKF. A similar approach has been suggested
by (Ko et al., 2007b), and (Ko et al., 2007a). They
estimated the trajectory of an autonomous blimp by
combining GPR with an UKF or ordinary differential
equations (ODE), respectively. Localization of wire-
less devices, like mobile telecommunication devices
or mobile robots is solved by modeling the probability
distribution of the signal strength with GPs integrated
in a BF (Ferris et al., 2006).
Several works employ information about the cur-
rent terrain conditions to improve the navigation sys-
tems of mobile robots. One intuitive approach is to
distinguish between traversable and non-traversable
terrain (Dahlkamp et al., 2006), (Rasmussen, 2002).
In contrast to the binary separation, Weiss et al.
(Weiss et al., 2006) are using a SVM to classify
the vertical accelerations and hence the terrain type.
Using spectral density analysis (SDA) and principal
component analysis (PCA) Brooks et al. (Brooks
et al., 2005) concentrate on the vibrations a mobile
robot experiences while driving. The preprocessed
data records are categorized through a voting scheme
of binary classifiers. Another way to analyse the driv-
ing conditions is to measure the slippage (Iagnemma
and Ward, 2009), (Ward and Iagnemma, 2007).
Kapoor et al. (Kapoor et al., 2007) are using GPs
with pyramid-match kernels to classify objects from
visual data. Urtasun and Darrell (Urtasun and Darrell,
2007) chose a GP latent variable model to achieve a
better classification by reducing the input dimension.
Although many works concentrate on position es-
timation as well as terrain classification, none com-
bined GPR and GPC to solve both problems at once
for a velocity controller of high speed outdoor robots.
3 GAUSSIAN PROCESSES
GPs are applicable to regression as well as classifica-
tion tasks. In contrast to other methods GPs do not
have any parameters that have to be determined man-
ually. However, the kernel function affects the prop-
erties of a GP essentially and must be chosen by hand.
The parameters of of GPs can be automatically opti-
mized using the training data. Furthermore, GPs pro-
vide uncertainty values additionally to the estimates.
These properties makes GPs attractive for regression
and classification task like position estimation and ter-
rain classification. However, a drawback of GPs is
their running time which is quadratic in the number of
training cases due to the inversion of the kernel ma-
trix.
3.1 Regression
Computing the predictive distribution of GPs consists
of three major steps. First, we determine the Gaussian
distribution of the training data and the test data. To
integrate the information of the training data into the
later distribution, we compute the joint distribution.
Finally, this joint distribution is transformed to the
predictive equations of GPs by conditioning it com-
pletely on the training data.
Let X = [x
1
,...,x
n
]
>
be the matrix of the n train-
ing cases x
i
. The measured process outputs are col-
lected in y = [y
1
,...,y
n
]
>
. The noise of the random
process is modeled with zero mean and variance σ
2
n
.
The kernel function is used to computed the similar-
ities between two cases. Our choice is the squared
exponential kernel given by
k(x
i
,x
j
) = exp(−
1
2
|x
i
− x
j
|
2
), (1)
where k is the kernel and x
i
, x
j
are two inputs. A fur-
ther quantity we need to provide the prior distribution
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
6

of the training data is the kernel matrix of the training
data K = K(X,X). It is given by K
i j
= k(x
i
,x
j
) using
the kernel function. Now, we are able to specify the
distribution of y:
y ∼ N (0, K + σ
2
n
I). (2)
We are trying to learn the underlying function of the
process. To get the distribution of the values of the
underlying function f = [ f
1
,..., f
n
]
>
we simply need
to neglect the noise term from the distribution of the
training data.
f ∼ N (0, K). (3)
Secondly, we determine the distribution of the test
data. Let X
∗
= [x
∗
1
,...,x
∗
n
∗
]
>
be the set of n
∗
test
cases assembled in a matrix like the training data.
f
∗
= [ f
∗
1
,..., f
∗
n
∗
]
>
are the function values of the test
cases. The normal distribution of the test data is there-
fore given by
f
∗
∼ N (0,K
∗∗
), (4)
where K
∗∗
= K(X
∗
,X
∗
) is the kernel matrix of the test
cases, representing the similarities of this data points.
To combine training and test data distributions in a
joint Gaussian distribution we further require the ker-
nel matrix of both sets, denoted by K
∗
= K(X, X
∗
).
Consequently, the joint distribution of the training and
test data is:
y
f
∗
∼ N
0,
K + σ
2
n
I K
∗
K
>
∗
K
∗∗
. (5)
This combination allows us to incorporate the knowl-
edge contained in the training data into the distribu-
tion of the function values of the test cases f
∗
, the
values of interest.
Since the process outputs y are known, we can
compute the distribution of f
∗
by conditioning it on
y, resulting in the defining predictive distribution of
GP models.
f
∗
|X,y,X
∗
∼ N (E[ f
∗
], V[ f
∗
]) (6)
with the mean and the variance given as
E[ f
∗
] = K
>
∗
[K + σ
2
n
I]
−1
y (7)
V[ f
∗
] = K
∗∗
− K
>
∗
[K + σ
2
n
I]
−1
K
∗
. (8)
The final distribution is defined only in terms of the
three different kernel matrices and the training targets
y.
3.2 Classification
The basic principle of GPC for multi-class problems
is similar to GPR. Yet GPC suffers from the prob-
lem that the class labels p(y| f ) are not Gaussian dis-
tributed. Hence, the distribution of the function values
given the training data
p( f |X ,y) =
p(y| f )p( f |X)
p(y|X)
(9)
Figure 2: Graphical model of our dynamic approach show-
ing the processing of the data and the dependencies between
the terrain classification and position estimation.
is also not Gaussian. X and f still denote the training
data and its function values, whereas y now represents
the class labels of the training data. Yet to use GPs we
have to have Gaussian distributed variables and must
approximate p( f |X,y), by the Laplace method for in-
stance. Once the approximation is done, the further
procedure is similar to GPR models, resulting in the
predictive distribution of the GPC models f
∗
|X,y,x
∗
.
Class probabilities are computed by drawing samples
from this final distribution and applying the softmax
function to squeeze the values into [0,1].
GPC have the same properties as GPR. The class
probabilities can be seen as a confidence value and
are perfectly suited to be combined with probabilistic
filters.
4 DYNAMIC APPROACH
Simple controller consider only one type of terrain or
use one averaged terrain model. In contrast, our ap-
proach considers the different effects on the kinemat-
ics of mobile robots caused by varying terrain condi-
tions. Our algorithm splits naturally in two parts, the
estimation of the robot’s position and the classifica-
tion of the terrain. Figure 2 shows a graphical model
of our dynamic approach.
4.1 Position Estimation
The position estimation consists of two methods. We
use GPs to do regression on the robot’s velocities and
an UKF to transfer the results into the position space.
The values used were provided by an IMU in-
stalled on the robot. A series of preceding experi-
ments were done to determine the composition of data
types which in combination with the projection into
POSITION ESTIMATION OF MOBILE ROBOTS CONSIDERING CHARACTERISTIC TERRAIN PROPERTIES
7
the position space allowed the best position estima-
tion. The data compositions compared in these exper-
iments varied in two aspects, first the type of the data,
and second the amount of past information.
The data combinations considered were: (1) the
change in x-direction
1
and y-direction, (2) the change
in x-direction, y-direction and in the orientation, (3)
the x-velocity and y-velocity, (4) the x-velocity, y-
velocity and the change in the orientation, (5) the
translational and rotational velocity, and (6) the trans-
lational and rotational velocity and the orientation
change. The number of past values was altered from 1
to 4 values to determine the minimal amount of previ-
ous information necessary for the system to be robust,
while at the same time does not cloud the data records
and does not complicate the learning task. Leading
to a total number of 24 different data compositions.
While differing in the motion model and complexity,
all approaches can be easily transformed into posi-
tions. However, some approaches suffer from a poor
transformation function, making them rather useless.
The results showed that a single past value of the
translational and rotational velocity works best for po-
sition estimation. Thus, the data records of the GPR
reads as follows:
[l
t−1
, l
t
, r
t−1
, r
t
, v
t−1
, ω
t−1
] (10)
Since our Longcross robot has a differential drive, l
i
and r
i
denote the values of the speed commands to
the robot for the left and right side of it’s drive. v
i
and
ω
i
represent the translational and rotational velocity,
respectively. To learn a controller we need both the
commands given to the robot and the implementation
of these commands. The values of interest are the cur-
rent velocities, v
t
and ω
t
.
We use GPR to solve this regression task which
not only provides the estimates of translational and
rotational velocities but also gives us uncertainty val-
ues. We transform the estimates into positions us-
ing an UKF. Additionally, the uncertainties are pro-
jected onto these positions and are propagated over
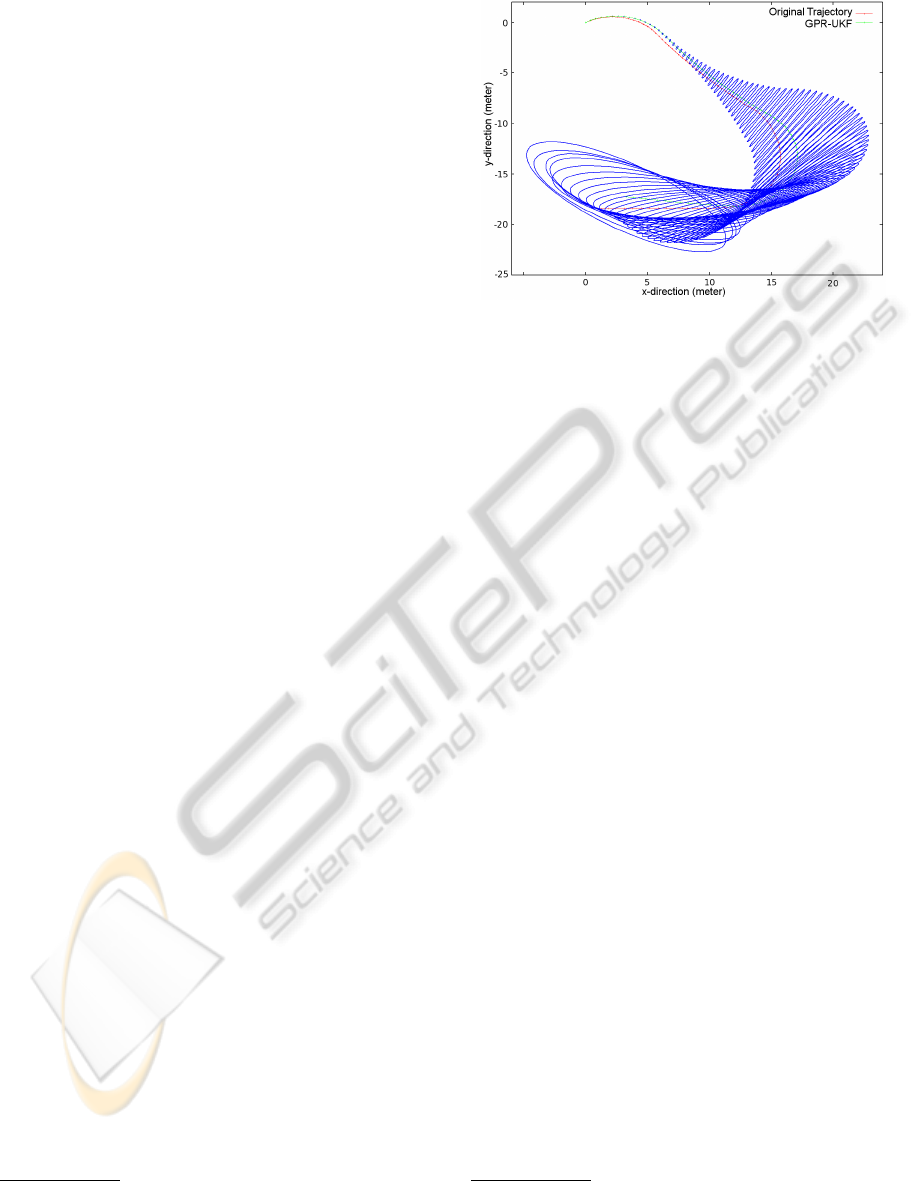
time (Figure 3). Starting with a quite certain position
the sizes of the error ellipses are increasing, due to
the uncertainties of the velocity estimates and the in-
creasing uncertainties of the previous positions they
rely on.
Given only the first translational and rotational ve-
locity, the regression does not rely on any further IMU
values. It takes previous estimates as inputs for the
next predictions. Assuming the first velocities to be
zero (i.e. the robot is standing) makes our approach
1
All directions are relative to the robot. The x-directions
points always in the front direction of the robot, and the y-
direction orthogonal laterally.
Figure 3: Original (red) and predicted (green) trajectory of
a 30 second drive. The UKF error ellipses are displayed in
blue. Starting out with a small uncertainty the error ellipses
(blue) increase over time, due to the uncertainty of previous
positions and the velocity estimates.
completely independent of the IMU device. However,
IMU data is required for training.
For each type of terrain we trained two
2
GPR
models with data recorded only on that terrain. This
has several advantages: Firstly, the effects of the robot
commands on a specific terrain can be learned more
accurately, since they are not contaminated by effects
on other terrain types. Secondly, in combination more
effects can be learned. And thirdly, due to the alloca-
tion of the training data to several GPR models the
size and complexity of each model is smaller com-
pared to what a single model covering all terrain types
would require. The classification described in the next
paragraph enables us to select the appropriate terrain
models for regression.
4.2 Terrain Classification
The terrain classification is implemented with a GPC
model, and a 2-step BF is used to model the transi-
tions between terrains and to smooth the classification
results.
As for the position estimation task preceding ex-
periments were conducted to determine the best suited
data records for the classification task. In contrast,
here are mainly two possible data types, the vertical
velocities and accelerations.
By taking a look at the raw IMU data it is evi-
dent that the different terrains are hardly distingush-
able and that it may need to be preprocessed. To be
sure, we classified vertical velocity and acceleration
records of varying sizes. Since the single values carry
2
GPs are not able to handle multi-dimensional outputs.
Hence, we need one GPR model for each velocity, transla-
tional and rotational.
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
8

no information about the terrain, we took vectors of
25, 30, 35, and 40 values. The results showed the raw
data to be improper for the classification task at hand.
The information about the terrain types is en-
closed in the vibrations a mobile robot experiences
while driving. We used the fast Fourier transform
(FFT) to extract the frequency information. Given
that the FFT works best with window sizes being a
power of 2, we chose 16, 32, 64, and 128 as input
lengths. Due to the symmetric structure of the FFT
output, it is sufficient to use only the first half of the
result. This reduces the complexity of the problem
and allows us to consider larger window sizes as for
the raw data. Using Fourier transformed vertical ve-
locities and accelerations improved the classification
results, as was expected. We found the vector of 128
vertical acceleration values to work best for our task.
Hence, the input to the GPC model is given by
[ f f taz
0
,..., f f taz
63
], (11)
where f f taz
i
denotes the ith value of the FFT result.
If the robot’s speed is too slow the terrain charac-
teristics are not longer present in the vibrations, and
therefore a good classification is impossible. Thus,
we omit data for which the robot’s translational ve-
locity is below some threshold τ.
Due to the native charaters of the terrains, the driv-
ing conditions vary within a terrain type. This makes
it hard to achieve a perfect classification. To deal with
false predictions and to account for the properties of
the classifier, we used a 2-step BF to model the transi-
tions between terrains. The quality values GPC mod-
els provide, come in terms of class probabilities which
are well suited to be included into a probabilistic fil-
ter like the BF. The defining equation of our 2-step BF
is slightly modified to accommodate the classification
and the dependency on two previous beliefs.
b(x
t|t−1
) ∝
∑
x
t−1|t−1
∑
x
t−2|t−2
p(x
t|t−1
|x
t−1|t−1
,x
t−2|t−2
) ·
b(x
t−1|t−1
) · b(x
t−2|t−2
) (12)
The notation x
t|t−1
denotes the value of the state x at
time t given all observations up to time t − 1. b(·)
is the belief, and p(x
t|t−1
|x
t−1|t−1
,x
t−2|t−2
) represents
the transition probabilities, i.e. the dependency on the
previous states. At this point the belief of the current
state x
t
depends only on the observations up to z
t−1
.
We include the current observation z
t
via the result of
the classifier c
t
.
b(x
t|t
) ∝
p(x
t|t−1
|c
t
,z
t
)p(c
t
|z
t
)
p(x
t|t−1
|z
t
)
· b(x
t|t−1
), (13)
where p(c
t
|z
t
) is the classification result. The output
of our BF is the belief of state x
t
given all observations
including z
t
. It considers the classification and two
previous states.
As already mentioned, the terrain classification is
used to determine on which terrain the robot is cur-
rently driving and hence which terrain model should
be used to estimate the next position. Since the robot
commands required for the position estimation are
given at a rate of approximately 3Hz, whereas the ter-
rain classification relies only on IMU data provided
at 100Hz, we implemented both parts to work inde-
pendently of each other. However, it takes about a
second to acquire enough data for classification, thus
we reuse the last terrain model until a new classifica-
tion is available. Below we will refer to the terrain
models used by the GPR as applied models to distin-
guish them from the fewer classifications which were
actually performed. Algorithm 1 summarizes our ap-
proach.
Algorithm 1. Dynamic Approach.
Input: initialized and trained GPR and GPC models
while sensor data q
∗
available do
2: get p
∗
and q
∗
from sensors
if p
∗
available and speed > τ then
4: s
∗
= FFT(p
∗
)
t
p
= GPC.classify(s
∗
)
6: b
p
= BF.process(t
p
)
model = selectModel(b
p
)
8: end if
[v,ω] = GPR.predict(model,q
∗
)
10: pos = UKF.process(v,ω)
publish(pos)
12: end while
The algorithm requires trained GP models. If sensor data
q
∗
is available, the algorithm predicts the velocity values
using the current terrain model. If sufficient vibration data
p
∗
is available for classification (omitting low speed data),
a new classification of the terrain will be performed and the
current model will be updated.
5 EXPERIMENTAL RESULTS
The Longcross (Figure 1) is an experimental platform
weighing about 340 kg with a payload capacity of at
least 150 kg. The compartment consists of carbon-
fibre and is environmentally shielded. Our version is
equipped with a SICK LMS 200 2D laser scanner, a
Velodyne Lidar HDL-64E S2 3D laser scanner, and
an Oxford Technical Solutions Ltd RT3000 combined
GPS receiver and inertial unit. The software runs on a
dedicated notebook with a Intel Core 2 Extreme Quad
processor and 8 GB memory.
POSITION ESTIMATION OF MOBILE ROBOTS CONSIDERING CHARACTERISTIC TERRAIN PROPERTIES
9
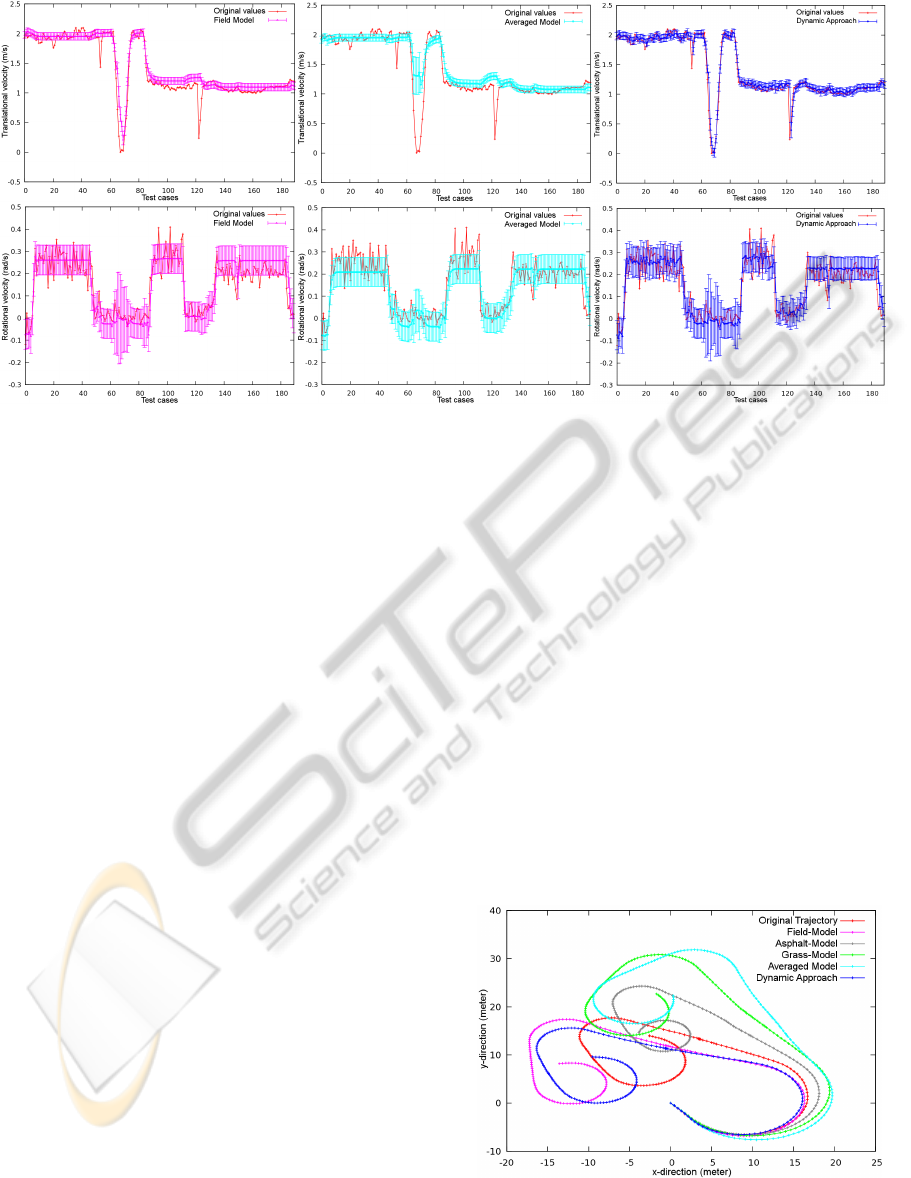
Figure 4: Estimation of the translational velocities (upper row), and of the rotational velocities (lower row) with error bars.
Even if the differences between the models are not significant, they result in rather distinct trajectories.
5.1 Simple Approaches
We evaluated our approach on a test drive covering
three different terrains, starting on field, continuing
with grass, and ending on asphalt. The test sequence
consists of 190 positions (about a 1 minute) almost
evenly partitioned on the three terrains. We compared
our dynamic approach to a field model, an asphalt
model, a grass model and an averaged model. The
first three models were trained only on the specific
terrain. The averaged model was trained on all three
terrains equally. All models used a total of 1500 train-
ing cases. The dynamic approach utilizes the three
terrain specific models.
We used the mean squared error (MSE) and the
standardized MSE to evaluate the quality of the re-
gression. The SMSE is the MSE divided by the vari-
ance of the test points, thus it does not depend on the
overall scaling of the values. The MSE is not applica-
ble to measure the quality of a trajectory because er-
rors at the beginning are propagated through the entire
trajectory influencing all proceeding positions. So we
introduced the mean segment distance error (MSDE).
First, we split the original trajectory and the predic-
tion in segments of fixed size. Each pair of segments
is normalized to the same starting position and orien-
tation. The distance of the resulting end positions is
computed subsequently. The mean of all these dis-
tances constitutes the MSDE. We found a segment
size of 10 to be a reasonable size.
The estimation results of the translational (upper
row) and the rotational velocities (lower row) of the
field model, the averaged model and of our dynamic
approach are shown in Figure 4. The field model is
the best of the simple models. The averaged model
would be the model of choice if one wants to con-
sider different terrain conditions but does not want to
employ a dynamic approach.
The estimation of the translational velocities by
the averaged model shows little or no reaction to
any of the outliers. Averaging the effects of com-
mands over several terrains involves diminishing ef-
fects of certain command-terrain combinations, hence
causing inaccurate estimates. The field model per-
forms best of the simple approaches, mainly because
it recognizes the slowdown around the 70th test case.
However, the other two outliers are not identified. The
estimates of the remaining test cases are similar to
the averaged model, yet the field model is slightly
superior. Our dynamic approach outperforms both
Figure 5: Predicted trajectories. Starting the models’ pre-
dictions are exact but differ increasingly along the time line,
leading to unlike trajectories.
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
10
Table 1: Prediction quality. The translational velocity unit
is m/s, the rotational velocity unit is rad/s, and the MSDE
unit is m.
Model MSE SMSE MSDE
10
v 0.02522 0.10588
Field
ω 0.00331 0.23605
0.42923
v 0.07032 0.29517
Asphalt
ω 0.00533 0.38034
0.56363
v 0.05161 0.21662
Grass
ω 0.00365 0.26041
0.51907
v 0.06203 0.26038
Averaged
ω 0.00377 0.26929
0.45478
v 0.01181 0.04956
Dynamic
ω 0.00279 0.19917
0.31407
previous models. In contrast, it recognizes all out-
liers, as the right terrain model is applied most of the
times. Additionally, the estimates of each test point
are pretty accurate.
The estimates of the rotational velocities give a
similar picture. The averaged model is somewhat off
at the beginning, underestimating the true values. The
field model is much more accurate. The error bars
seem to be larger than in the upper row but it is due
to the scale of the data. However, our approach again
provides the best estimation, reacting even to minor
changes in the velocity values.
The velocities are translated into positions using
an UKF. The resulting trajectories of all models tested
are shown in Figure 5. The previous tendencies are
reflected in the quality of the trajectories. The aver-
aged model’s trajectory is rather inaccurate, followed
by the trajectory of the field model which is outper-
formed by our dynamic approach. At the beginning
the predicted tracks are close, the differences start
during the first turn and increase by the time. Even
though the distinction between the velocity estimates
are relatively small, the impact on the trajectories are
formidable. Especially the rotation values are crucial
Figure 6: Classification results (upper image) and applied
models (lower image). The classification matches the se-
quence of field (red triangle), grass (green circles), and as-
phalt (grey squares) with high accuracy. Transitions are not
classifiable because the records contain data of two terrains.
Table 2: Classification results and applied models. F = field,
A = asphalt, G = grass.
Dynamic Approach Classification Applied Model
Correct Terrain 96.06% 96.45%
p(y = F|x ∈ F) 100.00% 100.00%
p(y = A|x ∈ A) 93.75% 93.84%
p(y = G|x ∈ G) 94.44% 95.52%
to the trajectory quality.
We analyzed the quality of the GPR estimations
of the velocities with the MSE and the SMSE. Due
to the reasons mentioned above, the trajectories are
evaluated by the MSDE. The results are presented in
Table 1.
We also examined the classification performance.
Figure 6 displays the results of the classification af-
ter applying the BF, and the terrain models used for
the regression. The figures show that the classifier
tends to categorize field as grass vibrations and grass
records as asphalt. One problem is that the field and
grass terrains are alike. At the low speed of approx-
imately 1 m/s the vibrations experienced on grass are
close to the ones recorded on asphalt. Nonetheless, al-
most all false classifications are compensated by the
BF.
Table 2 lists the classification quality in terms of
correct classifications and applied models. Also, the
classification rates are broken down into the classes
giving more insight.
5.2 Dynamic Approaches
In the previous section we compared our dynamic
approach to single terrain models, which by defini-
tion cannot be optimal when the robot drives on sev-
eral different terrains. Therefore, we constructed an-
other dynamic approach similar to the one presented.
By doing so, we combined a support vector machine
(SVM) to perform the regression of the velocities,
and a k-nearest neighbor (k-NN) method for classi-
fication. We chose to combine a SVM and k-NN be-
cause of their low runtimes. The conducted experi-
ments showed the overall runtime of the GP approach
to be a serious issue.
We omitted the UKF from the system because the
SVM does not provide any uncertainty values. These
values are essential to the UKF in order to work prop-
erly. However, we kept the 2-step BF, even though
the k-NN method usually returns simple class labels
rather than class probabilities. We counted the votes
for each class and divided them by the total number
of neighbors k to provide class probabilities anyway.
We used the LibSVM library (Chang and Lin, 2001)
POSITION ESTIMATION OF MOBILE ROBOTS CONSIDERING CHARACTERISTIC TERRAIN PROPERTIES
11
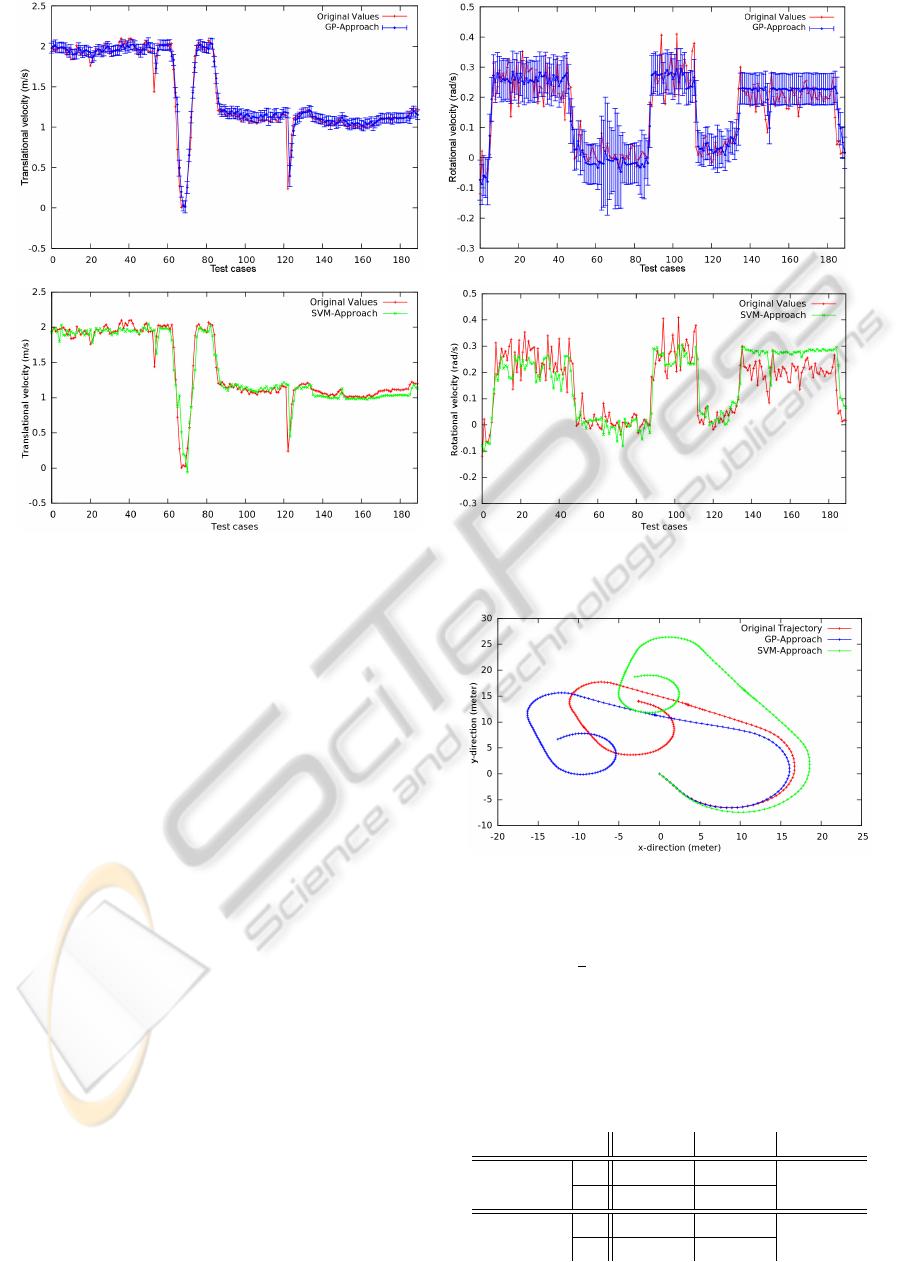
Figure 7: Comparison of the two dynamic approaches. Estimation of the translational velocities (left column), and of the
rotational velocities (right column) with error bars.
with a radial basis function (RBF) as SVM kernel and
found the OpenCV k-NN implementation with k = 8
neighbors to work best for vibrations.
To train the terrain models of the SVM we used
the same training data as we did for the GP models.
The training set of the classifiers are also unchanged.
Since this approach is able utilize several terrain
models for prediction, it should be more competitive
than the single terrain model approaches. To distin-
guish the two dynamic approaches, we will refer to
the GP based system as GP-Approach and to the SVM
and k-NN system as SVM-Approach.
The top row of Figure 7 shows the estimations of
the translational and rotational velocities by the GP-
Approach from the previous section. The prediction
results of the SVM-Approach are illustrated below.
Both dynamic approaches fit the original translational
velocities fairly accurately and recognize all outliers.
The estimation differences between the two systems
are somewhat more apparent when we concentrate on
the rotational velocities. The SVM-Approach under-
estimates the first part and overestimates the veloci-
ties towards the end. Its predictions are more agitated
in contrast to the averaging characteristic of the GP
estimations.
The observations are reflected in the error values
of Table 3. Even though the errors of the dynamic
approaches are very small - they are the smallest of
Figure 8: Predicted trajectories of the two dynamic ap-
proaches.
all tested models - the values of the SVM-Approach
are more than
1
3
higher. As we will see later, this is
partly due to the lower k-NN classification quality.
The SVM’s underestimation of the rotational ve-
Table 3: Prediction quality of the two dynamic approaches.
The translational velocity unit is m/s, the rotational velocity
unit is rad/s, and the MSDE unit is m.
Model MSE SMSE MSDE
10
GP v 0.01181 0.04956
Approach ω 0.00279 0.19917
0.31407
SVM v 0.01923 0.08073
Approach ω 0.00464 0.33089
0.30336
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
12

Table 4: Classification results of the two dynamic ap-
proaches. F = field, A = asphalt, G = grass.
Classification SVM-Approach GP-Approach
Correct Terrain 70.00% 96.06%
p(y = F|x ∈ F) 71.43% 100.00%
p(y = A|x ∈ A) 93.75% 93.75%
p(y = G|x ∈ G) 55.55% 94.44%
Table 5: Applied models of the two dynamic approaches. F
= field, A = asphalt, G = grass.
Applied Model SVM-Approach GP-Approach
Correct Terrain 75.26% 96.45%
p(y = F|x ∈ F) 71.70% 100.00%
p(y = A|x ∈ A) 91.04% 93.84%
p(y = G|x ∈ G) 62.86% 95.52%
locity corresponds to the assumption of a less sharper
turn. The green trajectory in Figure 8 shows exactly
this behavior. Furthermore, the higher estimated ro-
tational velocities at the end of the trajectory result in
tighter turns. Regardless of the rather different pre-
dictive trajectories, the trajectory qualities in Table 3
are almost the same.
With respect to the classification task the GP clas-
sifier performs much better than the k-NN classi-
fier. The sequence of classifications and applied
models are compared in Figure 9. While the GP-
Approach keeps the current terrain until enough ev-
idence is present that the terrain may have changed,
the SVM-Approach tends to change the terrain class
more quickly. This makes the system to apply the
wrong terrain model more often.
Table 4 and 5 point out that the k-NN classifier
struggles to distinguish grass and field records. Lead-
ing to a performance more than 25% worse than the
GP classification. Evaluating the quality of the ap-
plied models, we can see a slight improvement by
about 5%, still staying way behind our approach.
Figure 9: Comparison of the two dynamic approaches.
Classification results (upper image) and applied models
(lower image). Transitions are not classifiable because the
records contain data of two terrains.
As stated earlier the classification quality is cru-
cial to the performance of the overall system, since
false classifications lead to the application of wrong
terrain models, resulting in worse velocity estima-
tions. However, the SVM-Approach, incorporating
SVM regression and k-NN classification, is signifi-
cantly faster than our GP-Approach.
6 CONCLUSIONS
In this paper we introduced a dynamic approach to
estimate positions of a mobile robot. Since the ter-
rain conditions are crucial to the robot’s implemen-
tation of velocity commands, we consider the terrain
for the prediction of future positions. We used GPs
for the regression of translational and rotational ve-
locities. An UKF transfers the velocity estimates into
positions and propagates the uncertainties of the posi-
tions over time. The vibration affecting the robot are
classified by a GPC model in order to separate differ-
ent terrains. A 2-step BF is used to compensate for
classification errors and to model the terrain transi-
tions.
The prediction problem considered in this paper
has several difficult properties: first, with respect to
the classification task, the visual ground truth is not
always accurate. Due to natural terrain types, which
in themselves can be vastly different, vibrations in-
duced by separate terrains may sometimes look alike
or even show characteristics of another terrain. In a
consequence, making it tricky to evaluate the the clas-
sifier’s performance. Second, finding a reasonable di-
versity of terrains is quite challenging, which aggra-
vates the task of determining the transition probabili-
ties from real data.
Nevertheless, our approach proved to be more
effective than simple approaches utilizing a single
model for all terrains. Furthermore, our GP-Approach
is competitive with other dynamic approaches using
different machine learning techniques. The dynamic
systems, our GP-Approach and the slightly struc-
turally altered SVM-Approach, are both better than
all simple models, proving the basic idea of our ap-
proach to be well suited to solve such prediction prob-
lems.
Future work will be to reduce the run time. Due to
the use of GPs the entire systems suffers of a long run
time. Several sparse algorithms for GPs exist which
would help to improve this issue. Moreover, expand-
ing the current system by additional terrains as sand
or gravel would be desirable. Extending the classifi-
cation records by the translational velocity could im-
prove classification results, since it allows to learn the
POSITION ESTIMATION OF MOBILE ROBOTS CONSIDERING CHARACTERISTIC TERRAIN PROPERTIES
13

effects of different speeds on the vibrations.
REFERENCES
Agrawal, M. and Konolige, K. (2006). Real-time localiza-
tion in outdoor environments using stereo vision and
inexpensive GPS. In International Conference on Pat-
tern Recognition (ICPR), volume 3, pages 1063–1068.
Brooks, C. A., Iagnemma, K., and Dubowsky, S. (2005).
Vibration-based terrain analysis for mobile robots. In
IEEE International Conference on Robotics and Au-
tomation (ICRA), pages 3415–3420.
Burgard, W., Fox, D., Hennig, D., and Schmidt, T. (1996).
Estimating the absolute position of a mobile robot us-
ing position probability grids. In AAAI National Con-
ference on Artificial Intelligence, volume 2.
Chang, C.-C. and Lin, C.-J. (2001). LIBSVM: a library
for support vector machines. Software available at
http://www.csie.ntu.edu.tw/∼cjlin/libsvm.
Dahlkamp, H., Kaehler, A., Stavens, D., Thrun, S., and
Bradski, G. R. (2006). Self-supervised monocular
road detection in desert terrain. In Robotics: Science
and Systems.
Ferris, B., H
¨
ahnel, D., and Fox, D. (2006). Gaussian pro-
cesses for signal strength-based location estimation.
In Robotics: Science and Systems.
Girard, A., Rasmussen, C. E., Quinonero-Candela, J., and
Murray-Smith, R. (2003). Gaussian process priors
with uncertain inputs - Application to multiple-step
ahead time series forecasting. In Advances in Neural
Information Processing Systems (NIPS), pages 529–
536.
Iagnemma, K. and Ward, C. C. (2009). Classification-
based wheel slip detection and detector fusion for mo-
bile robots on outdoor terrain. Autonomous Robots,
26(1):33–46.
Kapoor, A., Grauman, K., Urtasun, R., and Darrell, T.
(2007). Active learning with gaussian processes for
object categorization. In IEEE International Confer-
ence on Computer Vision (ICCV), volume 11, pages
1–8.
Ko, J., Klein, D. J., Fox, D., and H
¨
ahnel, D. (2007a). Gaus-
sian processes and reinforcement learning for identifi-
cation and control of an autonomous blimp. In IEEE
International Conference on Robotics and Automation
(ICRA), pages 742–747.
Ko, J., Klein, D. J., Fox, D., and H
¨
ahnel, D. (2007b). GP-
UKF: Unscented Kalman filters with gaussian process
prediction and observationmodels. In IEEE/RSJ In-
ternational Conference on Intelligent Robots and Sys-
tems (IROS), pages 1901–1907.
Li-Juan, L., Hong-Ye, S., and Jian, C. (2007). Generalized
predictive control with online least squares support
vector machines. In Acta Automatica Sinica (AAS),
volume 33, pages 1182–1188.
MacKay, D. J. C. (1998). Introduction to gaussian pro-
cesses. In Bishop, C. M., editor, Neural Networks
and Machine Learning, NATO ASI Series, pages 133–
166. Springer-Verlag.
Rasmussen, C. E. (2002). Combining laser range, color, and
texture cues for autonomous road following. In IEEE
International Conference on Robotics and Automation
(ICRA).
Rasmussen, C. E. and Williams, C. K. I. (2005). Gaussian
Processes for Machine Learning. The MIT Press.
Seyr, M., Jakubek, S., and Novak, G. (2005). Neural net-
work predictive trajectory tracking of an autonomous
two-wheeled mobile robot. In International Federa-
tion of Automatic Control (IFAC) World Congress.
Thrun, S., Fox, D., Burgard, W., and Dellaert, F. (2000).
Robust monte carlo localization for mobile robot. Ar-
tificial Intelligence, 128:99–141.
Urtasun, R. and Darrell, T. (2007). Discriminative gaussian
process latent variable models for classification. In In-
ternational Conference on Machine Learning (ICML).
Ward, C. C. and Iagnemma, K. (2007). Model-based wheel
slip detection for outdoor mobile robots. In IEEE In-
ternational Conference on Robotics and Automation
(ICRA), pages 2724–2729.
Weiss, C., Fr
¨
ohlich, H., and Zell, A. (2006). Vibration-
based terrain classification using support vector ma-
chines. In IEEE/RSJ International Conference on
Intelligent Robots and Systems (IROS), pages 4429–
4434.
Williams, C. K. I. (2002). Gaussian processes. In The Hand-
book of Brain Theory and Neural Networks. The MIT
Press, 2 edition.
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
14
