FORMATION CONTROL BETWEEN A HUMAN AND A MOBILE

ROBOT BASED ON STEREO VISION

avio Garcia Pereira, Marino Frank Cypriano and Raquel Frizera Vassallo

Department of Electrical Engineering, Federal University of Esp

ırito Santo

Av. Fernando Ferrari, 514, Goiabeiras, Vit

oria-ES, CEP 29075-910, Brazil

Keywords:

Formation control, Stereo vision.

Abstract:

This paper presents a reactive nonlinear formation control between a human and a mobile robot based on stereo

vision. The human, who is considered the leader of the formation, is positioned behind the robot and moves

around the environment while the robot executes movements according to human movements. The robot has

a stereo vision system mounted on it and the images acquired by this system are used to detect the human

face and estimate its 3D coordinates. These coordinates are used to determine the relative pose between the

human and robot, which is sent to the controller in order to allow the robot to achieve and keep a desired

formation with the human. Experimental results were performed with a human and a mobile robot, the leader

and follower respectively, to show the performance of the control system. In this paper a load was put on a

mobile robot in which the nonlinear controller was applied, allowing the transportation of this load from a

initial point to a desired position. In order to verify the proposed method some experiments were performed

and shown in this paper.

1 INTRODUCTION

Navigating and following are the two basic function-

alities of mobile robots. Both of them are widely

studied topics. Many strategies have been developed

for several kinds of environments either with a sin-

gle agent systems or multi-agent systems (Bicho and

Monteiro, 2003; Das et al., 2002; Egerstedt and Hu,

2001; Egerstedt et al., 2001; Jadbabaie et al., 2002;

Vidal et al., 2003).

In most of these studies the robots are used to nav-

igate in order to reach a speciﬁc goal point in a given

environment while avoiding obstacles (Althaus et al.,

2004). However, due to limitations in sensing, most

times, robots are not able to operate in complex en-

vironments, even if they are provided with accurate

sensors like a 3D range ﬁnder. Therefore, we believe

that a human-robot navigation system is a good solu-

tion for this kind of problem, since human can lead

the robot in a cooperative task.

The motivation for the work presented in this pa-

per comes from situations where robots are used to

help people in an object transportation task where the

person does not load the object, only guides the robot

through the environment.

A new issue for navigation emerges from interac-

tion tasks, which concerns the control of the plat-

form (Althaus et al., 2004). The main idea is that the

robot’s behavior must be smooth and similar to the

human’s movements.

In human-robot interaction the actions of the robot

depend on the presence of humans and their wish to

interact.

In (Bowling and Olson, 2009) a human-robot team

is composed by two omnidirectional robots and one

human. The authors consider the case in wich a hu-

man turns abruptly a corner and the robots may keep

the human in their line of sight. The strategy is ac-

complished by taking the center of mass of the for-

mation and analyzing its rotation.

The work proposed in this paper consists in coor-

dinating the movements of a mobile robot by a human

in order to transport a load from a desired point to an-

other one in a safe way. In this system, the human,

which is considered the formation leader, is responsi-

ble for guiding the robot through the environment by

making the load transportation from an initial point to

a goal position and orientation. The robot (follower)

must move according to the human maitaining the for-

mation. This type of cooperative work needs the robot

to acquire enough information about the human posi-

tion to achieve the goal. This is reached through a

135

Garcia Pereira F., Frank Cypriano M. and Frizera Vassallo R. (2010).

FORMATION CONTROL BETWEEN A HUMAN AND A MOBILE ROBOT BASED ON STEREO VISION.

In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 135-140

DOI: 10.5220/0002880601350140

 SciTePress

vision-based nonlinear controller which estimates the

linear and angular velocities that the robot must exe-

cute to follow the human. This application is useful

because as the load is on the robot, the human does

not need to carry the object with it. The human func-

tion is to guide the robot through the environment.

Unlike the conventional leader-follower coopera-

tion, where commonly the formation leader is posi-

tioned in front of the follower(s), the formation con-

trol proposed in this work takes into consideration the

fact that the robot navigates in front of the human,

which is considered the leader of the formation. As

the formation control is based on vision, a stereo vi-

sion system is mounted on top of the robot pointing

backwards, which allows the robot to navigate “look-

ing” at the human face, instead of “looking” at the

back of the human. Another interesting point of this

formation is the fact that, since the robot goes in front

of the human (leader), the personn can observe the

robot behavior during the cooperation task and, in ad-

dition, can notice the presence of obstacles and guide

the robot in order to avoid them. This is something

valuable because we focused on the cooperation prob-

lem and still did not include an obstacle avoidance

algorithm to the robot behavior. That is one of our

issues for future work.

This paper is organized as follows. The technique

for estimating the face pose is brieﬂy discussed in

Section 2 and the formation controller as its stability

analysis are shown in Section 3. Some experimental

results are given in Section 4 and, ﬁnally, the conclu-

sions and future work are commented in Section 5.

2 HUMAN DETECTION

The nonlinear controller that will be presented in Sec-

tion 3 needs the distance from the human to the robot

(d) and the angle between the vector which links the

human position with the center of the robot (θ). In

order to estimate these two variables, it is used a cali-

brated stereo vision system attached to the robot. The

human pose is estimated by detecting the face in both

images captured by the vision system and, afterwards,

recovering its 3D coordinates.

The face detection is performed with the algo-

rithm proposed in (Viola and Jones, 2001), which

utilizes several images to train a detection algorithm

based on Adaboost. After detecting the face in both

images, an algorithm to detect some facial character-

istics is applied and the coordinates of these points in

the image plane are determined. Knowing the posi-

tions of these points in both images, their 3D coordi-

nates can be recovered. These facial features are, for

instance, the eyes, nose and mouth. Figures 1 (a) and

1 (b) show the images captured by the stereo vision

system and the detected facial features.

(a) (b)

Figure 1: Images captured by the stereo vision system.

The face coordinates is considered as being the av-

erage of the facial features coordinates, i. e.,

[X,Y, Z] =

∑

i=1

, y

, z

], (1)

where N is the number of detected features and

, y

, z

], are the 3D coordinates of each detected fa-

cial feature in the vision system reference frame at-

tached to the robot. Figure 2 illustrates the robot and

the stereo vision system reference frames.

Camera

Reference Frame

Robot

Reference Frame

Figure 2: Robot and vision system reference frames.

The relation between these coordinate frames is

given by a rotation of 180

◦

around the x-axis and a

translation of 1.2m in the y-axis. Thus,

= T

(1.2)R

(180)C

(2)

where R

and C

are respectively the coordinates in

the robot reference frame and in the camera reference

frame.

After estimating the 3D coordinates of the face,

the variables d and θ are calculated on the vision sys-

tem’s XZ-plane (ground plane). Figure 3 shows the

human and the vision system positions in the XZ-

plane.

The values of d and θ, that deﬁne the distance and

the angle between the human and the robot, are deter-

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

136

Person

(0, 0, 0)

Vision System

(X, Y, Z)

Figure 3: Human and vision system position in the XZ-

plane.

mined as











d =

√

+ Z

θ = atan





(3)

where X and Z are, respectively the x and z coor-

dinates of the face. Notice that, however d and θ

where calculated in the camera frame, they are valid

in the robot frame, due to the aligment between the

two frames.

3 CONTROLLER

The aim of the proposed controller is to keep the robot

with a desired distance and orientation to the human

partner in order to accomplish a speciﬁc task. That

is done by using the information obtained from the

pair of images provided by the stereo vision system

assembled on the robot.

Figure 4 illustrates a mobile robot with a stereo

vision system attached to it and one person behind

it. Considering this case, the kinematic equations that

describe the robot movement with respect to the per-

son are given by











d = v

−v

cos(θ)

θ = ω +

sin(θ)

sin(

θ)

(4)

where v

and ω are, respectively, the robot linear and

angular velocities, v

is the human velocity, d is the

distance between the person and the vision system

while θ is the angle of the human face according to

the stereo vision system frame and

θ is the angular

error.

The values of d and θ are obtained from the 3D

coordinates of the middle of the face after 3D recon-

struction. The way to obtain these values was ex-

plained in Section 2.

After determining d and θ, the distance and orien-

tation errors (

θ) are calculated as

Stereo Vision

System

Person

Figure 4: Relative position between the robot and the per-

son.







d = d

−d

θ = θ

−θ,

(5)

where d

and θ

are respectively the desired distance

and orientation that the robot has to keep from the

human.

For the presented system, it is proposed a nonlin-

ear controller in order to accomplish the objective of

control, i. e, to keep the robot following the human

with speciﬁed distance and orientation. For this con-

troller, the linear and angular velocities are











cos(θ)



−k

tanh(



ω = k

tanh(

θ) −v

sin(θ)

−v

sin(

θ)

(6)

with k

, k

> 0.

The control structure used in this work appears in

Figure 5. The operations of detecting faces and facial

features, recovering the 3D coordinates and determin-

ing the values of d and θ, are executed by the “Image

Processing” block.

Control Robot

Image

Processing

Figure 5: Control structure.

3.1 Stability Analysis

For the nonlinear controller proposed in (6) the fol-

lowing candidate Lyapunov function is taken to check

the system stability

V (

θ) =

, (7)

FORMATION CONTROL BETWEEN A HUMAN AND A MOBILE ROBOT BASED ON STEREO VISION

137

which is positive semi-deﬁned and has the following

time-derivative function

V (

θ) =

d +

θ. (8)

Thus, differentiating (5) with respect to time and

replacing the result in (8) we will have

V (

θ) = −

d −

θ. (9)

Now, the values of

d and

θ in (9) are substituted

by the respective values from (4). Then we have

V (

θ) = −

d[v

−v

cos(θ)]−



ω+

sin(θ)

sin(

θ)



(10)

Replacing the control actions proposed (6) in (10),

the time-derivative of the Lyapunov function is rewrit-

ten as

V (

θ) = −k

tanh(

d −k

tanh(

θ)

θ. (11)

As mentioned k

and k

are positive, and func-

tions like x.tanh(x) ≥ 0 ∀ x. So, (8) is negative semi-

defined, which means the asymptotic stability of the

proposed nonlinear controller, i. e.,

θ → 0 when

t → ∞.

Notice that to estimate the angular velocity it is

necessary to know the human velocity, v

. This ve-

locity can be estimated as

≈

d(t) −d(t −1)

∆t

−v

cos(

θ). (12)

4 EXPERIMENTAL RESULTS

In order to prove the reliability of the proposed

method, some experiments were performed and two

of them will be shown in this section. These exper-

iments were performed with a mobile robot Pioneer

3AT from ActivMedia Robotics, a stereo vision sys-

tem built with two USB web cameras, which provide

images with 320x240 pixels. The control system is

written in C++ and each control loop is executed in

250ms. The robot with the stereo vision system used

to perform the experiments can be seen in Figure 6.

4.1 Experiment 1

In this experiment, the human leads the robot from

the initial position, which has coordinates (X , Z) =

(0m, 0m) to the coordinates (X, Z) = (3m, −5m)

through a “S-like” path. The trajectory described by

the robot can be seen in Figure 7.

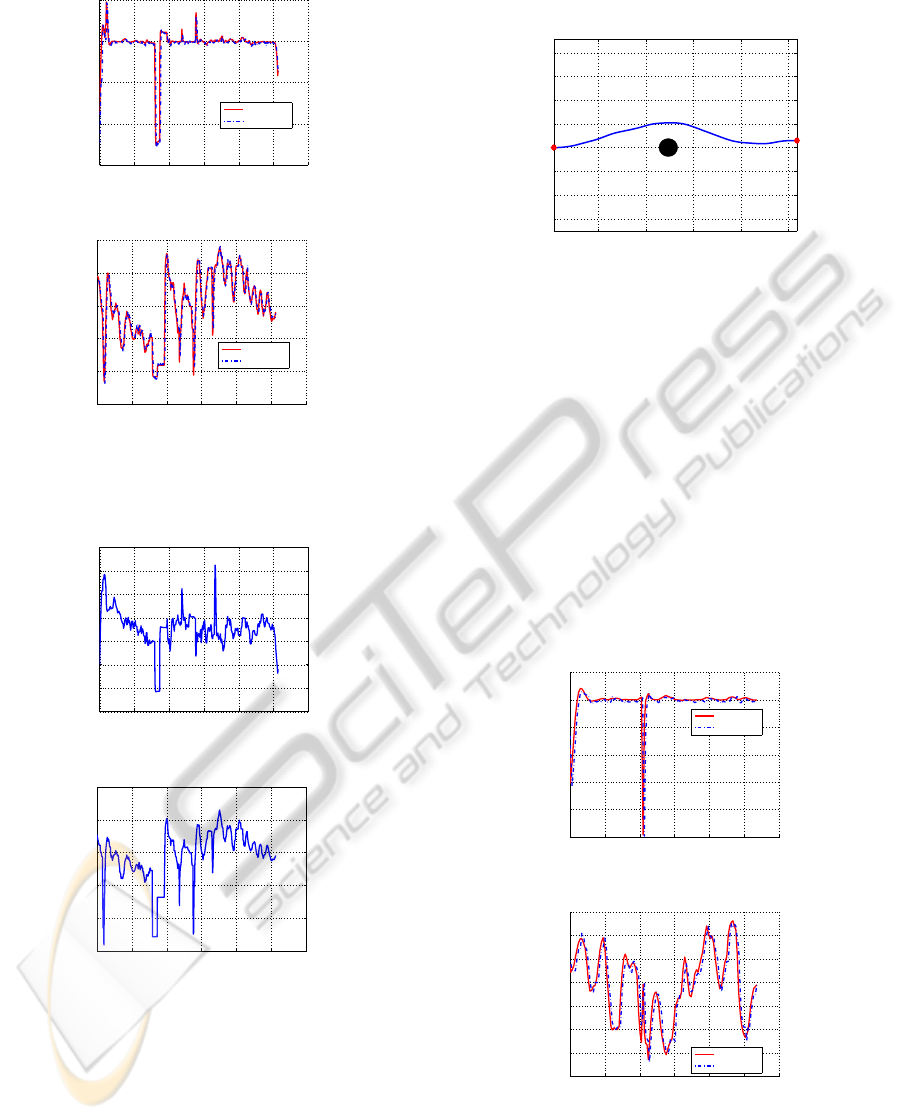
The linear and angular velocities performed by the

robot are shown, respectively, in Figures 8 (a) and (b).

Figure 6: Robot used to perform the experiments.

−1 0 1 2 3 4

−4

−3

−2

−1

Trajectory Described by the Robot

x [m]

y [m]

Figure 7: Experiment 01: Trajectory described by the robot.

The continuous line represents the velocities calcu-

lated by the controller and the velocities performed

by the robot are plotted as dashed line.

In Section 3.1 the control system stability was

demonstrated, i. e., it was proved that the system er-

rors tend to zero when the time grows and if the hu-

man stops at some place. In order to illustrate this,

the graphics shown in Figure 9 present the errors dur-

ing the experiment. Figure 9 (a) shows the distance

error during the experiment while the angular error is

presented in Figure 9 (b).

By observing Figure 7 it is possible to see that

the robot reached the goal describing desired trajec-

tory. Moreover, as can be seen in Figure 9, both the

distance error and the orientation error tend to zero,

which means the robot accomplished the task. For

the next experiments, the errors will not be shown.

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

138

0 20 40 60 80 100 120

−50

100

150

Linear Velocity

t [s]

v [mm/s]

Calculated

Performed

(a)

0 20 40 60 80 100 120

−15

−10

−5

Angular Velocity

t [s]

w [deg/s]

Calculated

Performed

(b)

Figure 8: Experiment 01: Velocities performed by the

robot. Linear (a) and Angular (b).

0 20 40 60 80 100 120

−0.1

0.1

0.2

0.3

0.4

0.5

0.6

Distance Error

t [s]

error [m]

(a)

0 20 40 60 80 100 120

−60

−40

−20

Angular Error

t [s]

error [deg]

(b)

Figure 9: Experiment 01: Distance error (a) and Angular

error (b).

4.2 Experiment 2

In this experiment the human should guide the robot

from the initial position (X , Y ) = (0m, 0m) to the ﬁ-

nal coordinates (X, Y ) = (5m, 0m). However, there

was a circular obstacle with diameter equal to 0.4m.

The trajectory described by the robot during the exe-

cution of this task is shown in Figure 10.

1 2 3 4 5

−1.5

−1

−0.5

0.5

1.5

Trajectory Described by the Robot

x [m]

y [m]

Figure 10: Experiment 02: Trajectory described by the

robot.

It is important to mention that the robot does not

have an obstacle avoidance algorithm. So, the devia-

tion that can be seen in Figure 10 occurred due to the

human action, i. e., the person who leads the robot no-

ticed an object in the middle of the desired trajectory

and guided the robot in order to deviate from it. Even

though it seems that the person has to walk in an un-

natural way in order to prevent the robot from crash-

ing into obstacles or corner in a hallway, this problem

will be solved by adding an obstacle avoiding strategy

such as in (Chuy et al., 2007; Pereira, 2006).

The linear velocity is shown in Figure 11 (a) while

the angular velocity appears in Figure 11 (b).

0 10 20 30 40 50 60

100

120

Linear Velocity

t [s]

v [mm/s]

Calculated

Performed

(a)

0 10 20 30 40 50 60

−8

−6

−4

−2

Angular Velocity

t [s]

w [deg/s]

Calculated

Performed

(b)

Figure 11: Experiment 02: Velocities performed by the

robot. Linear (a) and Angular (b).

Notice that around the 20th second of the experi-

FORMATION CONTROL BETWEEN A HUMAN AND A MOBILE ROBOT BASED ON STEREO VISION

139

ment, both linear and angular velocities calculated by

the controller are equal to zero. This happened be-

cause in this instant, the robot lost the information

about the person for, at least, one of the cameras of

the stereo vision system. This behavior was adopted

in order to avoid having the robot be out of control ev-

ery time the vision system loses the information about

the human. Thus, whenever the robot loses the infor-

mation about its leader, it stops and waits for a new

face detection.

Although an obstacle in the middle of the desired

trajectory, the human managed to guide the robot to

avoid this object and reach the desired point.

5 CONCLUSIONS AND FUTURE

WORK

This paper presented an approach to a formation con-

trol between a human and a mobile robot using stereo

vision. The strategy uses the recognition method pre-

sented by (Viola and Jones, 2001) in order to ﬁnd the

facial features needed to estimate the human position.

A stable nonlinear controller is proposed to allow the

robot to perform the task in cooperation with a hu-

man. The effectiveness of the proposed method is

veriﬁed through experiments where a human guides

the robot from an initial position to a desired point,

when the human moves either forward or backwards.

Our future work is concerned in improving the

features detection in order to better estimate the hu-

man position and orientation. Besides, we also intend

to introduce a second robot to the formation. Thus,

the robots will be able to carry a bigger and heavier

load.

REFERENCES

Althaus, P., Ishiguro, H., Kanda, T., Miyashita, T., and

Christensen, H. (2004). Navigation for human-robot

interaction tasks. In ICRA ’04. 2004 IEEE Interna-

tional Conference on Robotics and Automation, 2004.

Proceedings., volume 2, pages 1894–1900 Vol.2.

Bicho, E. and Monteiro, S. (2003). Formation control for

multiple mobile robots: a non-linear attractor dynam-

ics approach. In Intelligent Robots and Systems, 2003.

(IROS 2003). Proceedings. 2003 IEEE/RSJ Interna-

tional Conference on, volume 2, pages 2016–2022

vol.2.

Bowling, A. and Olson, E. (2009). Human-robot team dy-

namic performance in assisted living environments.

In PETRA ’09: Proceedings of the 2nd International

Conference on PErvsive Technologies Related to As-

sistive Environments, pages 1–6, New York, NY, USA.

ACM.

Chuy, O., Hirata, Y., and Kosuge, K. (2007). Environment

feedback for robotic walking support system control.

In ICRA, pages 3633–3638.

Das, A., Fierro, R., Kumar, V., Ostrowski, J., Spletzer,

J., and Taylor, C. (2002). A vision-based formation

control framework. Robotics and Automation, IEEE

Transactions on, 18(5):813–825.

Egerstedt, M. and Hu, X. (2001). Formation constrained

multi-agent control. In Robotics and Automation,

2001. Proceedings 2001 ICRA. IEEE International

Conference on, volume 4, pages 3961–3966 vol.4.

Egerstedt, M., Hu, X., and Stotsky, A. (2001). Control of

mobile platforms using a virtual vehicle approach. Au-

tomatic Control, IEEE Transactions on, 46(11):1777–

1782.

Jadbabaie, A., Lin, J., and Morse, A. (2002). Coordination

of groups of mobile autonomous agents using nearest

neighbor rules. In Decision and Control, 2002, Pro-

ceedings of the 41st IEEE Conference on, volume 3,

pages 2953–2958 vol.3.

Pereira, F. G. (2006). Navegac¸

ao e desvio de obst

aculos us-

ando um rob

o m

ovel dotado de sensor de varredura

laser. Master’s thesis, Universidade Federal do

Esp

ırito Santo - UFES.

Vidal, R., Shakernia, O., and Sastry, S. (2003). Formation

control of nonholonomic mobile robots with omnidi-

rectional visual servoing and motion segmentation. In

Robotics and Automation, 2003. Proceedings. ICRA

’03. IEEE International Conference on, volume 1,

pages 584–589 vol.1.

Viola, P. and Jones, M. (2001). Rapid object detection us-

ing a boosted cascade of simple features. Proceed-

ings of the 2001 IEEE Computer Society Conference

on Computer Vision and Pattern Recognition, 2001.

CVPR 2001., 1:I–511–I–518 vol.1.

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

140