EXTRACTING OBJECTS BY CLUSTERING OF FULL PIXEL

TRAJECTORIES

Hisato Aota, Kazuhiro Ota, Yuichi Yaguchi and Ryuichi Oka

Department of Computer and Information Systems, University of Aizu, Tsuruga, Aizu-Wakamatsu, Japan

Keywords:

Object tracking, Object segmentation, Pixel-wise matching, Motion feature.

Abstract:

We propose a novel method for the segmentation of objects and the extraction of motion features for moving

objects in video data. The method adopts an algorithm called two-dimensional continuous dynamic pro-

gramming (2DCDP) for extracting pixel-wise trajectories. A clustering algorithm is applied to a set of pixel

trajectories to determine objects each of which corresponds to a trajectory cluster. We conduct experiments

to compare our method with conventional methods such as KLT tracker and SIFT. The experiment shows that

our method is more powerful than the conventional methods.

1 INTRODUCTION

Tracking and segmentation of moving objects in

video are veryimportantfor many tasks, such as video

surveillance and event inference. Humans are the

principal actors in daily activities, or locomotion (e.g.,

walking, running and standing), and so human mo-

tion is a key class within the ﬁeld of computer vision.

Many approaches for object tracking and segmenta-

tion have been proposed. These differ from each other

primarily in the way they approach the problem. Ap-

proaches depend on such aspects as the target objects,

context and environment in which tracking is per-

formed and the end use for which tracking informa-

tion is being sought. Yilmaz(Yilmaz et al., 2006) de-

clared object tracking as the problem of estimating the

trajectories of objects that are moving continuously in

an image sequence from initial frame to end frame.

In addition, the estimation must maintain a consistent

division of objects in the continuous image sequence

with segmentation. It must be also able to provide ob-

ject information such as area, orientation or shape. In

previous methods, continuous trajectories can only be

generated by detecting objects, which makes it hard to

track objects from data. The difﬁculty of this problem

is the difﬁculty of ﬁxing units of trajectories in time-

sequential images. The problem becomes even more

difﬁcult when the movement trajectories are extracted

from the object area with inadequate region detection.

Much of the previous research concentrated on ex-

tracting objects from background areas. We felt that

an alternative method based on pixel tracking would

not be as restricted as the previous methods.

In our laboratory, we developed a method named

two-dimensional continuous dynamic programming

(2DCDP), which can deﬁne full pixel correspon-

dences between two images. By using this approach,

it became possible to extract trajectories of all the pix-

els in an initial frame in time-sequential images. Next,

to extract effective trajectory groups from these, we

used two strategies. The ﬁrst is to remove the trajecto-

ries of background pixels, and the second is to cluster

the trajectories that are not removedand to group sim-

ilar trajectories. The goal of our work is to prove that

our proposed method can track and segment moving

objects without object detection or recognition, and

without pre-knowledge of the state of an object, its

motion or environmental factors such as people walk-

ing nonlinearly or complex human motions. To prove

the method’s beneﬁts, we demonstrate an effective

full-pixel matching method and connect its outputs.

Experimental results indicate that it is possible to ex-

tract pixel trajectories of objects and segment them by

clustering trajectories.

2 RELATED WORK

Many methods for object tracking have been pro-

posed. Examples include tracking methods with pre-

knowledge of an object’s state, using Haar-like fea-

tures(VIOLA, 2001), HOG features or mean-shift

colour features using a statistical classiﬁer (boost-

ing) detector(Mochiki and Katto, 2007) (Nakagawa

Aota H., Ota K., Yaguchi Y. and Oka R. (2010).

EXTRACTING OBJECTS BY CLUSTERING OF FULL PIXEL TRAJECTORIES.

In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 65-72

 SciTePress

et al., 2009)(Takeuchi et al., 2009). In addition,

Mikami(Dan et al., 2009) proposed a memory-based

particle ﬁlter(M-PF), which can visually track mov-

ing objects that have complex dynamics. It provided

robustness against abrupt head movements and re-

covered quickly from tracking failure caused by oc-

clusions. Yamashita’s(Takayoshi et al., 2008) pro-

posed tracking method with a soft decision feature

(EHOG) and online real boosting improved tracking

performance in scenes with human poses and posture

changes.

Deterministic methods for point correspondence

using object tracking based on feature points deﬁne

a cost of associating each object in frame t − 1 to

a single object in frame t by using a set of mo-

tion constraints. Rabaud(V. Rabaud, S. Belongie,

2006) developed a highly parallelized version of the

KLT tracker(Shi and Tomasi, 1994) that combined

graph cuts and RANSAC clustering and was able

to count objects in crowds. Sugimura(Sugimura

et al., 2009) proposed a human tracking method

with trajectory-based clustering with a gait feature

by KLT corresponding points and Delaunay triangu-

lation. Tsuduki(Tsuduki et al., 2007)(Yuji and Hi-

ronobu, 2009) used mean-shift searching to track a

point based on the information obtained by a SIFT

(Lowe, 2004), and obtained a better tracking perfor-

mance than KLT because a SIFT feature is invariant to

changes caused by rotation, scaling, and illumination.

3 SYSTEM OVERVIEW

In this section, we describe each system for this pro-

posed method. First, 2DCDP extracts full pixel cor-

responding points between frame of t and t + 1. Then

connecting corresponding points with outputs of all

frames by 2DCDP, it generate full pixel trajectories.

Then thresholding trajectories, it divides trajectories

into two groups which is moving objects trajectories

and background trajectories. Finally, divided trajec-

tories are extracted and its of moving objects are ex-

tracted by incremental clustering (Figure1).

Figure 1: Proposed Work Flow.

3.1 2DCDP Algorithm

2DCDP(Yaguchi et al., 2009) is an extension of

CDP(Oka, 1998) to 2D correlation, and is an effec-

tive algorithm for full-pixel matching (Figure 3). The

pixel coordinates of the input image S and reference

image R are deﬁned by:

S , {(i, j)|1 ≤ i ≤ I, 1 ≤ j ≤ J} (1)

R , {(m, n)|1 ≤ m ≤ M, 1 ≤ n ≤ N} (2)

The pixel value at location (i, j) of the input im-

age S

is S

(i, j) = {r, g, b}, and the pixel value

at location (m, n) of the reference image R

(m, n) = {r, g, b}, where r, g, and b are nor-

malized red, green, and blue values respectively,

and (0 ≤ { r, g, b} ≤ 1). We deﬁne the mapping

R → S, (m, n) ∈ R and (ξ(m, n), η(m, n)) ∈ S by

(m, n) =⇒ (ξ(m, n), η(m, n)), set the end location for

pixel matching as

i = ξ(M, N),

j = η(M, N) and

the point (

j) as a nomination of the spotting point

that is determined at the M + N − 1th iteration of the

proposed algorithm. Next, we set the local distance

d(i, j, m, n) as the difference value between S

(i, j)

and R

(m, n), and set w(i, j, m, n) as the weighted

value of each local calculation. In this implemen-

tation, the local distance is deﬁned as d(i, j, m, n) =

(i, j) − R

(m, n))

, and weights are set to 1 for all

paths (Figure 5). The accumulated local minimum

D(i, j, m, n) is used to evaluate the decision sequence,

and is deﬁned as:

j, m, n) =

min

ξ,η

{

∑

m=1

∑

n=1

w(ξ(m, n), η(m, n), m, n)

d(ξ(m, n), η(m, n), m, n)} (3)

Then ξ

∗

(m, n) and η

∗

(m, n) are used to represent the

optimal solutions in ξ(m, n) and η(m, n) respectively,

where W is the optimal accumulated weight W =

∑

m,n

w(ξ

∗

(m, n), η

∗

(m, n), m, n). To ensure continu-

ity and monotonicity, K(m, n) = {ξ(m− 1, n), η(m−

1, n)} and L(m, n) = {ξ(m, n − 1), η(m, n − 1)} are

used to deﬁne the sets of points that are movable in the

i and j directions in the input image, taken from the

movements in the m and n directions in the reference

image. The following equation deﬁnes the relation-

ship between two corresponding pixels (m− 1, n− 1)

and (m, n) (see Figure 4):

(ξ(m− 1, n − 1), η(m− 1, n− 1)) ∈

K(m, n) ⊗ L(m− 1, n) ∩ L(m, n) ⊗ K(m, n− 1) (4)

Here, the operator ⊗ represents the connection be-

tween a set of points on the left and a set of points on

the right. To calculate the accumulated local distance,

each accumulated local minimum D(i, j, m, n) is de-

rived from two previous accumulated local minima

D(i

′

, j

′

, m− 1, n) and D(i

′′

, j

′′

, m, n− 1). In this way,

we deﬁne the rank l = m + n − 1, as shown in Fig-

ure 2 (b), to calculate the accumulated local minimum

smoothly. Note that, for the accumulation and back-

tracking, 2DCDP selects two local paths to check

the connection of the four points (m, n), (m − 1, n),

(m, n− 1), and (m− 1, n − 1) that form a quadrangle

(Figure 4 ).

Spotting point

Input image

(i,j)

Reference image

(m,n)

Optimal path

Object and segmentation

area projections

Segmentation area

Rank

l = (m + n -1)

Rank

8 7

Rank

A nod e depends on

two lower-lank nodes

Reference

image

Corresponding pixels

Segmentation area

Input images

(a) Example of full pixel matching

(b) Determination of segmented area obtained by projecting

optimal paths in the 3D space (i, j, l) on the input image

Figure 2: Full pixel matching overview. (a) An example of

full pixel matching; (b) Optimal paths are able to explain a

3D space (i, j, l) in the input image. l is the rank used in the

expression l = m+ n− 1.

+ = 䋭

-45㫦5 2

0㫦4 1 7

+45㫦6 3

4 1 7

5 2

6 3

Row direction Column direction

),()),1(),,1(( nmKnmnm =−− ηξ

),())1,(),1,(( nmLnmnm =−− ηξ

(a) Two direction and seven path patterns for 2DCDP

Figure 3: Two directions and seven paths for selecting opti-

mal path to accumulate value.

Input image

(i,j)

Reference image

(m,n)

)1,(),(),1(),( −⊗∩−⊗ nmKnmLnmLnmK

))1,(),1,((),( −−= nmnmnmL ηξ

)),1(),,1((),( nmnmnm −−= ηξ

)),(),,((),( nmnmji ηξ=

(b) Example explaining the roles of K(m,n) and L(m,n)

Figure 4: One case (linear matching) among the possible

cases for optimal matching of local images, which include

many different cases of nonlinear optimal matching of local

areas.

m-direction:

n-direction:

1 1 1

),1),,1(),,1(( nmnmnmD −−− ηξ

),),,(),,(( nmnmnmD ηξ

),( nmK

),( nmL

)1,),1,(),1,(( −−− nmnmnmD ηξ

Weight function

),),,(),,(( nmnmnmw ηξ

Figure 5: Seven-path map and weight. All weights w are set

to 1 in implementation, but this can be changed.

L(m,n):

Candidate point group

of (ξ(m,n-1), η(m,n-1))

K(m,n):

Candidate point group

of (ξ(m-1,n), η(m-1,n))

(K(m,n)⊗L(m-1,n))

∩(L(m,n)⊗K(m,n-1)):

Candidate point group of

(ξ(m-1,n-1), η(m-1,n-1))

(ξ(m,n), η(m,n))

(d) Candidate conditions for neighboring pixels

Figure 6: Each i and j direction can connect seven candidate

pixels as (a) and (c). 2DCDP selects the node that has a

minimal accumulation value from among these paths, but a

node has depending on only two lower-rank nodes.

3.2 Connecting Corresponding Points

To extract the trajectories of the pixels in the ﬁrst

frame, we showed that frame (i

, j

) at time t and

frame (m

, n

) at time t + 1 are the points that cor-

respond by 2DCDP. Therefore, the correspondence

points in the following frame are derived for all the

pixels in the ﬁrst frame, and the following frame is

processed similarly, the trajectory of the ﬁrst-frame

pixels in the time sequence of images can be de-

termined. However, if both (i

, j

) and (i

, j

) at

time t correspond to (m

, n

) at time t + 1, they are

connected. As a result, the number of trajectories

decreases.(Figure7)

- i

m2,n2, - i2,j2

- i

m4,n4, - i4,j4

- i

m6,n6, - i6,j6

- i

m2,n2, - i2,j2

- i

m4,n4, - i4,j4

- i

m6,n6, - i6,j6

- i

m2,n2, - i2,j2

- i

m4,n4, - i4,j4

- i

m6,n6, - i6,j6

- i

m2,n2, - i2,j2

- i

m4,n4, - i4,j4

- i

m6,n6, - i6,j6

- i

x1 1,y11 - x12 ,

x1 3,y13 - x1 4,y1 4 - x15 ,y15

x2 1,y21 - x22 ,

x2 3,y23 - x2 4,y2 4 - x25 ,y25

x3 1,y31

x3 2,

32 - x33 ,y33 - x44,y44 - x55,y55

x4 1,y41 - x42 ,

x4 3,y43 - x4 4,y4 4 - x45 ,y45

x5 1,y51 - x52 ,

x5 3,y53 - x5 4,y5 4 - x55 ,y55

xn1,yn1 - xn2 ,

xn3,yn3 - xn4,yn4 - X5,yn5

t = 0 t = 1 t = k-1 t = k

Pixel Trajectories

Figure 7: Connecting corresponding points.

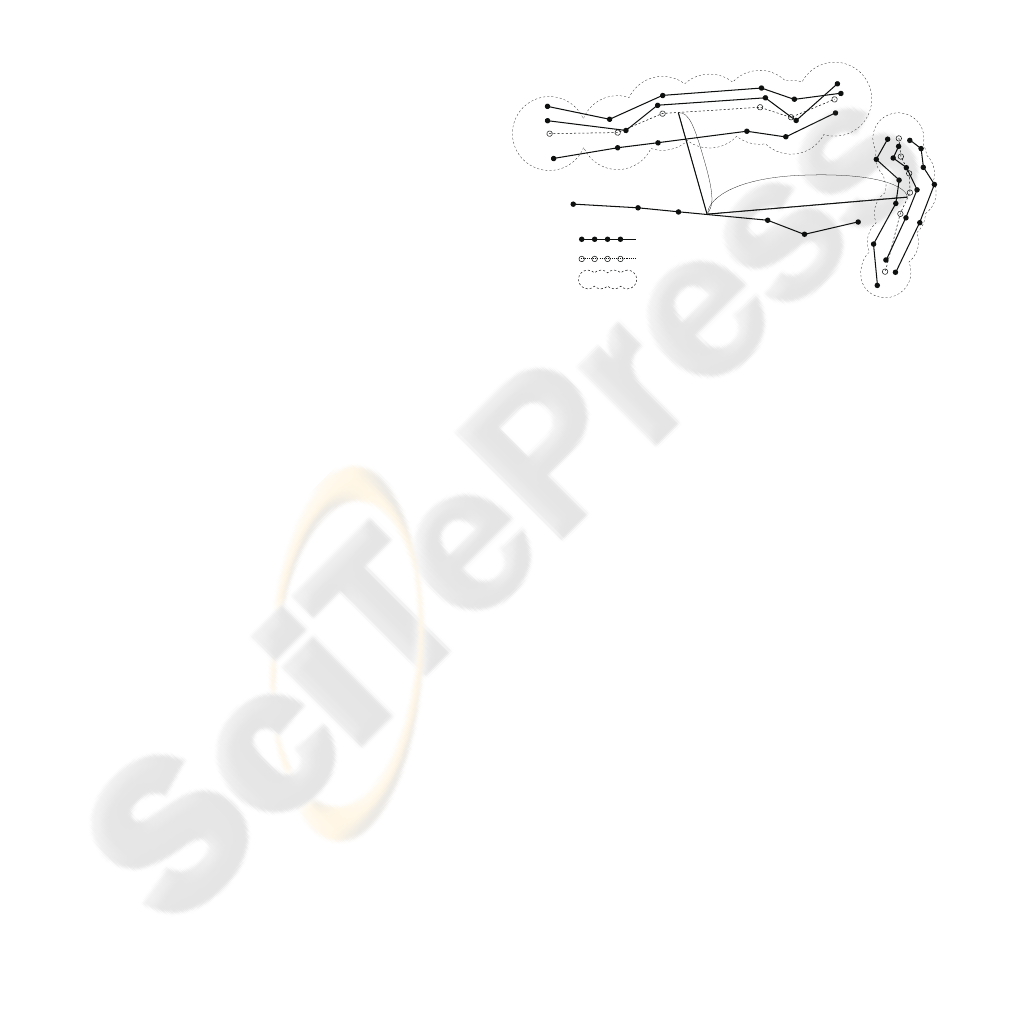
3.3 Filtering Trajectories for Clustering

In order to erase stationary trajectories, we calculate

spatial moving length for each trajectory. The length

is determined by the parameter mxy which is deﬁned

by mxy = max(max

− min

, max

− min

where a trajectory is represented by a location se-

quence,

, y

), (x

, y

), ..., (x

, y

). We introduce a thresh-

old value T. The trajectory with a larger length T is

erased for clustering. The parameter T is determined

by a heuristic method to each time-sequential image.

3.4 Trajectory Clustering

Incremental clustering is based on the basic sequen-

tial algorithm scheme (Gonzalez and Woods, 2001).

It ﬁnds and determines trajectories that have smaller

distances than the threshold value between their tra-

jectories and the cluster-center trajectory. Then, it

calculates the object-centred trajectory of each clus-

ter. These clusters include only trajectories that match

the threshold.

(1) The ﬁrst cluster includes the ﬁrst trajectory in the

threshold ranges.

(2) The Euclidean distance between the cluster-center

trajectory and the newly found trajectory is calcu-

lated. Using Euclid norm the distance between tra-

jectories, C(i) = (c

, c

), (c

, c

). . . (c

, c

)

and C( j) = (c

), (c

, c

). . . (c

, c

), is deﬁned by:

d(i, j) = ||C(i) −C( j)|| (5)

(3) A new cluster is created if a newlyfound trajectory

is not within a radius of the centered trajectory within

which clusters were created before. Otherwise, the

newly found trajectory is included in the nearest clus-

ter.

(4) Whenever a trajectory is included in a cluster,

the cluster-center trajectory is recalculated as an aver-

age of members’ trajectories. This incrementally in-

creases the size of the cluster. The algorithm repeats

(1)-(4), and ends when the last trajectory is processed

(Figure 8, 9).

3.5 Merging Clusters

A cluster, may be separated into two or more

clusters during the distance calculation of incre-

mental clustering, and so the clusters are merged

in post-processing. If the calculated distance of

the average trajectory of two clusters stays con-

stant or decreases, the two clusters are consid-

ered to form one. k is the frame number. Us-

ing Euclid norm the distance between cluster1 and

m = 1

= {x

}

For i = 2toN

- IF(d(x

, C

) ≥ Θ)AND(m ≤ q)then

m = m+ 1

= {x

}

-Else

= C

∪ {x

}

update mean of C

-End {IF}

-End{For}

Figure 8: Algorithm for Incremental Clustering.

Figure 9: Incremental Clustering.

cluster2 average trajectories, describes Center(i) =

, c

), (c

, c

). . . (c

, c

) and Center( j) =

, c

), (c

, c

). . . (c

, c

), is deﬁned by:

d(i, j) = ||Center(i) −Center( j)|| (6)

4 EXPERIMENTS

4.1 Experiment Speciﬁcation

4.1.1 Machine Environment

The computer used for the experiments was a Dell

Precision (CPU.Xeon 3.16 GHz Dual CPU proces-

sors; memory, 64 GB DDRAM; operating system,

CentOS and a 300 GB HDD). The video camera was

a Cannon IXY DIGITAL 920 IS.

4.1.2 Data Sets

Our research was tested on four different datasets

that we prepared. The video frame rate was 10 fps.

Because of the computer memory limitation, images

used in the experiments were resized to low resolution

using Lanczos ﬁlter. The datasets were as follows.

Figure 10: Result of Experiment 1. Three persons are well separated.

Figure 11: Result of Experiment 2. It can extract complex trajectories well.

• Three people walking in different directions.

Frame count is 107 and he image size is 200*150.

T is 50.

• Two people walks difference nonlinearly by each

direction . Frame number is 183. Image size is

200× 150. T is 30.

• Arms moving simultaneously. Frame count is 98,

image size is 200× 150. T is 40.

• Roller coaster with water splash. Frame count is

17. Image size is 288× 192. T is 20.

Figure 12: Result of Experiment 3. Two arms are separated.

Figure 13: Result of Experiment 4. Roller coaster, water splash and water surface are well separated.

4.2 Results

Below are illustrations of the conditioned trajecto-

ries for times t

to t

for each data set(Figure. 10–

13). Note that, the amplitude of the z-axis has been

changed for convenience. Each different color indi-

cates a different object corresponding to a cluster.

4.3 Comparison with KLT Tracker and

SIFT Tracker

Figure(14) shows the corresponding points and tra-

jectories in 3D space in which z-axis represents time.

The corresponding points, which are generated by

KLT and SIFT, appear discontinuously and the num-

ber of them less than that of 2DCDP, for those rea-

sons, trajectories of those corresponding points can-

not be generated by adapting connecting system. In

this comparison, we used Stan Birchﬁeld’s KLT(Stan,

2009) and Rob Hess’s SIFT(Hess, 2009) implementa-

tions.

Figure 14: Comparing with KLT Tracker and SIFT. Corre-

sponding points of KLT and SIFT are plotted to the left ﬁg-

ure, and trajectories of those coresponding points are plot-

ted to the right ﬁgure by adapting connecting system.

4.4 Discussion

In these experiments, density trajectories of simple

or complex movements could be acquired even with

low-resolution time-sequential images. The proposed

method is effective even for different movements by

two or more objects. Moreover, even if the movement

changed during the sequence, trajectories could still

be extracted. Even when objects have varying texture

and edges such that features cannot be detected, the

proposed method can still acquire trajectories for cor-

responding points. We also showed that the proposed

method is more effective than methods based of fea-

ture points such as KLT or SIFT, because 2DCDP can

identify many more accurate corresponding points

than KLT Tracker or SIFT Flow(Figure14). Further-

more, our method also ﬁnds trajectories even for non-

linear, complex, and detailed movement such as wave

splashes and the surface of the water (Figure13).

5 CONCLUSIONS

We havecreated a novelframework for extracting mo-

tion features from time-sequential images in a few

steps. We also developed an optimal full-pixel match-

ing method called two-dimensional continuous dy-

namic programming (2DCDP) that achieved image

recognition that supports segmentation for free and

full pixel matching. We applied 2DCDP to object

tracking and utilized data for corresponding points

provided by 2DCDP as input for extracting pixel tra-

jectories and could compute density trajectories of

moving objects. We were able to extract trajectories

and segment objects from various type of motion with

low resolution over many frames. Finally, we vali-

dated advantages of the proposed method (2DCDP +

trajectory Clustering).

6 FUTURE WORK

The present approach has not considered occlusion

and decreasing trajectories. Therefore, when objects

appear in succession on the screen, the trajectory of

a rear object is integrated into that of a front object.

Because only a few pixels represent the object trajec-

tories are integrated over time, and so the number of

trajectories decreases. If the resolution of the time-

sequential images increases so that the number of pix-

els forming the target object is increased, many trajec-

tories can be calculated more accurately. Further, the

time space is divided and clusters can re-form in each

time space, and so the decrease in number of trajecto-

ries can be reduced if the clustering results are merged

through the time axis. It is also necessary to remove

outlier noise trajectories to improve the accuracy.

This method is applicable for background detec-

tion and subtraction from video captured by a moving

camera. By analysing a vector ﬁeld and extracting the

majority 2DCDP vector, our method can divide back-

ground and foreground. It is able to apply a presump-

tion of camera motion. The majority vector ﬁeld is the

background, which can be removed to target moving

objects. Our experiments indicate that we can also

consider applying the method to gesture recognition

and to novel human interface such as lip reading and

expression recognition.

ACKNOWLEDGEMENTS

I express my gratitude to members of the Image Pro-

cessing Laboratory for their cooperation in experi-

ments.

REFERENCES

Dan, M., Kazuhiro, O., and Junji, Y. (2009). Memory-

based particle ﬁlter for face pose tracking robust under

complex dynamics. Proc. of IEEE CVPR2009, 0:999–

1006.

Gonzalez, R. C. and Woods, R. E. (2001). Digital Im-

age Processing Second Edition. Prentice-Hall Inter-

national.

Hess, R. (2009). Sift feature detector. http://web.engr.orego

nstate.edu/∼hess/.

Lowe, D. G. (2004). Distinctive image features from scale-

invariant keypoints. Int. Journal of Computer Vision,

60(2):91–110.

Mochiki, R. and Katto, J. (2007). Human tracking by par-

ticle ﬁlter using haar-like feature. Proc. of the IEICE

General Conference, 2007(2):121.

Nakagawa, H., Habe, H., and Kidode, M. (2009). Efﬁcient

prior acquisition of human existence by using past hu-

man trajectories and color of image. Technical report

of IEICE. PRMU, 108(484):305–312.

Oka, R. (1998). Spotting method for classiﬁcation of real

world data. The Computer Journal, 41(8):559–565.

Shi, J. and Tomasi, C. (1994). Good features to track. In

Proc. of IEEE Conference on CVPR1994, pages 593 –

600.

Stan, B. (2009). KLT: an implementation of

the kanade lucas tomasi feature tracker.

http://www.ces.clemson.edu/∼stb/klt/index.html.

Sugimura, D., Kitani, K. M., Okabe, T., Sato, Y., and Sugi-

moto, A. (2009). Tracking people in crowds based on

clustering feature trajectories using gait features and

local appearances. In Proc. of MIRU2009, pages 135–

142.

Takayoshi, Y., Hironobu, F., Shihong, L., and Masato, K.

(2008). Human tracking based on soft decision feature

and online real boosting. In Proc. of MIRU2008, pages

12–19.

Takeuchi, D., Ito, Y., Yamashita, A., and Kaneko, T. (2009).

Multi-viewpoint person tracking based on face detec-

tion of arbitrary pose and mean-shift algorithm. ITE

Technical Report, 33(11):69–72.

Tsuduki, Y., Fujiyoshi, H., and Kanade, T. (2007). Mean

shift-based point feature tracking using sift. IPSJ SIG

Technical Reports, 49(6):101–108.

V. Rabaud, S. Belongie (2006). Counting Crowded Moving

Objects. In Proc. of IEEE CVPR 2006, volume Vol. 1,

pages 705–711.

VIOLA, P. (2001). Rapid object detection using a boosted

cascade of simple features. Proc. of IEEE CVPR2001,

pages 511–518.

Yaguchi, Y., Iseki, K., and Oka, R. (2009). Optimal Pixel

Matching between Images. In Proc. of PSIVT 2009,

pages 597–610.

Yilmaz, A., Javed, O., and Shah, M. (2006). Object track-

ing: A survey. ACM Computing Surveys (CSUR),

38(4).

Yuji, T. and Hironobu, F. (2009). A method for visualizing

pedestrian trafﬁc ﬂow using sift feature point tracking.

In Proc. of IEEE PSIVT2009.