NAVIGATION AND FORMATION CONTROL EMPLOYING

COMPLEMENTARY VIRTUAL LEADERS FOR COMPLEX

MANEUVERS

Martin Saska, Vojtˇech Von´asek and Libor Pˇreuˇcil

Department of Cybernetics, Czech Technical University in Prague, Technick´a 2, Prague, Czech Republic

Keywords:

Autonomous mobile robots, Compact formations, Virtual leaders, Trajectory planning.

Abstract:

Complex maneuvers of formations of car-like autonomous vehicles are investigated in this paper. The proposed

algorithm provides a complete plan for the formation to solve desired tasks and actual control inputs for each

robot to ensure collision-free trajectories with respect to neighboring robots as well as dynamic obstacles.

The method is based on utilization of complementary virtual leaders whose control inputs are obtained in one

merged optimization process using receding horizon control methodologies. The functionality of the system,

which enables reverse driving and arbitrary rotations of formations of nonholonomic robots, is veriﬁed by

simulations of multi-robot tasks and by hardware experiments.

1 INTRODUCTION

In this paper, we present a novel approach for a non-

holonomic robots formation driving and a trajectory

planning to reach a target region. The method al-

lows arbitrary maneuvers, including reverse driving

and turning of the formation in limited environment

with static as well as dynamic obstacles. Such skills

are crucial for the control of autonomous ploughs dur-

ing cooperative airport snow shoveling (Saska et al.,

2008; Hess et al., 2009) being our target applications.

Tasks for which autonomous vehicles in formation

are used usually involve physical constraints imposed

by the vehicles (mobility constraints) or physical ob-

stacles (environment constraints) and constraints en-

forced by inter vehicle relations (shape of the forma-

tion). Thus, it is important for control methodolo-

gies to incorporate system’s constraints into the con-

trollers design while preserving overall system sta-

bility which makes the Receding Horizon Control

(RHC) especially appealing. Receding horizon con-

trol (also known as model predictivecontrol) is an op-

timization based control approach often used for sta-

bilizing linear and nonlinear dynamic systems (e.g.,

see (Alamir, 2006) and references reported therein).

For a detailed survey of RHC methods we refer to

(Mayne et al., 2000) and references reported therein.

The works applying RHC for formation driving con-

trol are presented in (Dunbar and Murray, 2006)

(Franco et al., 2008). These papers have utilized RHC

for the formationforming and/or followingpredeﬁned

trajectory in a workspace without obstacles. We will

apply the Receding Horizon Control for the virtual

leaders trajectory planning to desired goal area and

for the followers stabilization in the formation.

Our contribution is a general approach that ac-

counts for a nonholonomic robots’ formation stabi-

lization and a trajectory planning (enforced by a sta-

bility constraint) to reach a target region, also con-

sidering the response to dynamic changes in the en-

vironment. We developed a new concept of RHC by

combining both, the trajectory planning to the desired

goal region and the immediate control of the forma-

tion, into one optimization process. Our method can

continuously respond to changes in environment of

the robots while the cohesion of the immediate con-

trol inputs with direction of the formation movement

in future is kept. Furthermore, we extended the com-

mon leader-follower concept with the idea of two vir-

tual leaders, one for the forward and one for the back-

ward movement. Such an approach is necessary for

the complicated maneuvers of the formation of car-

like robots. The proposed method provides a com-

plete plan together with decisions when and how often

to switch between the guidance of the virtual leaders.

141

Saska M., Von

asek V. and P

reu

cil L. (2010).

NAVIGATION AND FORMATION CONTROL EMPLOYING COMPLEMENTARY VIRTUAL LEADERS FOR COMPLEX MANEUVERS.

In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 141-146

 SciTePress

2 PRELIMINARIES

Let ψ

(t) = {x

(t),y

(t),θ

(t)} denote the conﬁgu-

ration of a virtual leader R

at time t,

and ψ

(t) =

(t),y

(t),θ

(t)}, with i ∈ {1, . ..,n

}, denote the

conﬁguration for each of the n

followers R

time t. The Cartesian coordinates (x

(t),y

(t)), j ∈

{1,...,n

,L} for an arbitrary conﬁguration ψ

(t) de-

ﬁne the position ¯p

(t) of a robot R

and θ

(t) denotes

its heading. Let us assume that the environment of

the robots contains a ﬁnite number n

of compact ob-

stacles collected in a set of regions O

obs

. Let us also

deﬁne a target region S

as a circle with radius r

and

centerC

such that O

obs

∩S

0. Finally, we need to

deﬁne a circular detection boundary with radius r

and

a circular avoidance boundary with radius r

, where

> r

. Single robots should not respond to obsta-

cles detected outside the region with radius r

. On the

contrary, distance between the robots and obstacles

less than r

is considered as inadmissable. These con-

cepts are adopted from the concept of avoidance con-

trol (Leitmann, 1980) to be used in this paper for the

collision avoidance guaranties. Moreover, we need to

extend these zones for the virtual leaders depending

on size of the formation to ensure that the result of

the leader trajectory planning is feasible also for the

followers. We will denote the extended radiuses as

s,L

and r

a,L

2.1 Kinematic Model and Constraints

The kinematics for any robots R

, j ∈ {1,...,n

,L},

in the formation is described by the simple non-

holonomic kinematic model: ˙x

(t) = v

(t)cosθ

(t),

˙y

(t) = v

(t)sinθ

(t),

(t) = K

(t)v

(t), where ve-

locity v

(t) and curvature K

(t) represent control in-

puts ¯u

(t) = (v

(t),K

(t)) ∈ R

Let us deﬁne a time interval [t

N+M

] con-

taining a ﬁnite sequence with N + M + 1 el-

ements of nondecreasing times T (t

N+M

) =

,...,t

N−1

,...,t

N+M−1

N+M

}, such that

< t

< ... < t

N−1

< t

< ... < t

N+M−1

< t

N+M

Also, let us deﬁne a controller for a robot

starting from a conﬁguration ψ

) by

N+M

,T (·)) := { ¯u

− t

), ¯u

−

),..., ¯u

N+M−1

N+M

− t

N+M−1

)} which is char-

acterized as a sequence of constant control actions.

Each element ¯u

; t

k+1

−t

), k ∈ {0,...,N+M−1},

Index L denotes the virtual leader which has assigned

the leadership at the moment while indexes L

and L

dis-

tinguish between particular virtual leaders only if it is nec-

essary.

The meaning of constants N and M will be explained

in Section 3.

of the ﬁnite sequence U

N+M

,T (·)) will be held

constant during the time interval [t

k+1

) with length

k+1

− t

(not necessarily uniform).

By integrating the kinematic model in over a given

interval [t

N+M

], and holding constant control in-

puts over each time interval [t

k+1

) (from this point

we may refer to t

using its index k), we can derive

the following model for the transition points at which

control inputs change:

(k+1) =











(k) +

(k+1)



sin



(k)+

(k+1)v

(k+1)∆t(k+ 1)



−

sin



(k)



,ifK

(k+1) 6= 0;

(k) + v

(k+1)cos



(k)



∆t(k + 1),

if K

(k+1) = 0

(k+1) =











(k) −

(k+1)



cos



(k)+

(k+1)v

(k+1)∆t(k+ 1)



−

cos



(k)



,ifK

(k+1) 6= 0;

(k) + v

(k+1)sin



(k)



∆t(k + 1),

if K

(k+1) = 0

(k+1) = θ

(k) + K

(k+1)v

(k+1)∆t(k+ 1),

(1)

where x

(k) and y

(k) are the rectangular coordinates

and θ

(k) the heading angle for the conﬁguration

(k) at the transition point with index k, v

(k + 1)

and K

(k + 1) are control inputs at time index k + 1,

and ∆t(k + 1) is the sampling time. This model and

notation allows us to describe long trajectories exactly

using a minimal amount of information such as: i) the

initial conﬁgurationψ

), ii) the sequence of switch-

ing times T (·), and iii) the sequence of controls ac-

tions U

(·).

In real applications, the control inputs are lim-

ited by vehicle mechanical capabilities (i.e., chas-

sis and engine). This constraints can be taken into

account for each robot R

, j ∈ {1,...,n

,L}, limit-

ing their control inputs by the following inequalities:

min, j

≤ v

(k) ≤ v

max, j

and |K

(k)| ≤ K

max, j

, where

max, j

is the maximal forward velocity of the j-th ve-

hicle, v

min, j

is the limit on the backward velocity and

max, j

is the maximal control curvature. These values

can be different for each robot R

2.2 Formation Driving using RHC

The presented approach relies on the well known

leader-follower method frequently used in applica-

tions of car like robots (Barfoot and Clark, 2004).

In the method, the followers R

, i ∈ {1,...,n

} track

the leader’s trajectory which is distributed within the

group. The followers are maintained in relative dis-

tance to the leader in curvilinear coordinates with two

axes p and q, where p traces the leader’s trajectory

and q is perpendicular to p as is demonstrated in Fig-

ure 1. The positive direction of p is deﬁned from R

back to the origin of the movement and the positive

p = p = p

q 0=

Figure 1: Formation described by curvilinear coordinates p

and q.

direction of q is deﬁned in the left half plane in direc-

tion of the forward movement.

The shape of the formation is then uniquely deter-

mined by the parameters p

(t) and q

(t), deﬁned for

each follower i, which can vary during the mission.

To convert the state of the followers in curvilinear co-

ordinates to the state in rectangular coordinates, the

simple equations in (Barfoot and Clark, 2004) can be

applied.

The main idea of the receding horizon control is to

solve a moving ﬁnite horizon optimal control problem

for a system starting from current states or conﬁgura-

tion ψ(t

) over the time interval [t

] under a set of

constraints on the system states and control inputs. In

this framework, the length t

− t

of the time interval

] is known as the control horizon. After a so-

lution from the optimization problem is obtained on

a control horizon, a portion of the computed control

actions is applied on the interval [t

,δt

+ t

], known

as the receding step, where δt

:= ∆tn.

This pro-

cess is then repeated on the interval [t

+ δt

]

as the ﬁnite horizon moves by time steps deﬁned by

the sampling time δt

, yielding a state feedback con-

trol scheme strategy. Advantages of the receding time

horizon control scheme become evident in terms of

adaptation to unknown events and change of strategy

depending on new goals or new events such as appear-

ing obstacles in the environment.

3 METHOD DESCRIPTION

In this section, a concept of complementary virtual

leaders, which enables backward driving of forma-

tions, will be proposed. The basic idea of the classical

leader-follower concept (see Figure 1) is based on the

fact that the followers continue with forward move-

ment until the place where the leader changed the po-

larity of its velocity. Such a behavior could cause col-

lisions or unacceptable disordered motion leading to

Number of applied constant control inputs n is chosen

according to computational demands as was explained in

(Saska et al., 2009).

a breakage of the shape of formation. Natural con-

ception of the formation movement supposes that the

entire group keeps compact shape and so all mem-

bers should change the polarity of their velocity in the

same moment.

Such an approach requires an extension of the

standard method employing one leader to an approach

with two virtual leaders, one for the forward move-

ment and one for the backward movement. Their

leading role is switched always when the sign of the

leader’s velocity is changed. The suspended virtual

leader becomes temporarily a virtual follower. The

virtual follower traces the virtual leader similarly as

the other followers to be able to undertake its leading

duties at time of the next switching. Therefore, all

robots in our system will be considered as followers

and there is no physical leader. The virtual leaders

will be positioned at the axis of the formation, one in

front of the formation and one behind the formation.

In the presented approach, we propose to solve

collision free trajectory planning and optimal control

together for both virtual leaders in one optimization

step. This ensures integrity of the solution for the

separated plants. Beyond this, we extend the stan-

dard RHC method with one control horizon into an

approach utilizing two ﬁnite time intervals T

and T

The ﬁrst time interval T

should provide immediate

control inputs for the formation regarding the local

environment. By applying this portion of the control

sequence, the group is be able to respond to changes

in workspace that can be dynamic or newly detected

static obstacles. The difference ∆t(k+1) = t

k+1

−t

kept constant (later denoted only ∆t) in this time inter-

valand should satisfy the requirementsof the classical

receding horizon control scheme.

The second interval T

takes into account infor-

mation about the global characteristics of the environ-

ment to navigate the formation to the goal and to au-

tomatically compose the entire maneuver containing

usually multiple switching between the virtual lead-

ers. Here, we should highlight that also the number

of switchings between the virtual leaders is designed

automatically via the optimization process. The tran-

sition points in this part can be distributed irregularly

to effectively cover the environment. During the op-

timization process, more points should be automat-

ically allocated in the regions where a complicated

maneuver of the formation is needed. This is enabled

due to the varying values of ∆t(k+ 1) = t

k+1

− t

that

will be for the compact description collected into the

vector T

∆

L,M

= {∆t(N + 1), ...,∆t(N + M)}.

To deﬁne the trajectory planning problem with

two time intervals in a compact form we need to

gather states ψ

(k),k ∈ {1,...,N} and ψ

(k),k ∈

{N + 1,...,N + M} into vectors Ψ

L,N

∈ R

and

L,M

∈ R

. Similarly the control inputs ¯u

(k),k ∈

{1,...,N} and ¯u

(k),k ∈ {N + 1,...,N + M} can be

gathered into vectors U

L,N

∈ R

and U

L,M

∈ R

In the case of the direction of movement alterna-

tion, the formation has to travel into the distance

max

i={1...n

}

to place the second virtual leader on

the position of the ﬁrst one. Such a movement cre-

ates an

appendix

in the entire trajectory that is fol-

lowed. The minimal length of this additional tra-

jectory is deﬁned by the size of the formation and

only the curvature of the leading robot is not uniquely

determined. Therefore, we have to deﬁne a vector

App

collecting variables K

App

( j),∀ j ∈ {1,...,N +

M − 1} applied for the movement of the virtual lead-

ers in the appendixes. N + M − 1 is maximal pos-

sible number of switchings. Usually the number of

switchings is signiﬁcantly lower and the unused val-

ues of K

App

(·) will not be considered in the evalu-

ation of the optimization vector. All variables de-

scribing the complete trajectory from the actual po-

sition of the ﬁrst virtual leader until target region

can be then collected into the unique optimization

vector Ω

= [Ψ

L,N

,Ψ

L,M

∆

L,M

App

] ∈

6N+7M−1

.u The vector Ω

contains necessary infor-

mation for both leaders, but we have to decide, which

part of the vector will be assigned to which leader.

Firstly, let us deﬁne an ordered set of indexes of

samples where the polarity of velocity is changed as

:= {i : v

(i)v

(i+1) < 0},∀i∈ {1,...,N+M−1},

where the values of v

(·) can be extracted from the

vector U

L,MN

= [U

L,N

L,M

] ∈ R

2(N+M)

. Now, we

can propose to collect the control inputs used for

the ﬁrst virtual leader as U

,MN

= [ ¯u

(1), ¯u

(2),

..., ¯u

(1)), ¯u

App

(1), ¯u

(2) + 1),

¯u

(2) + 2), . . ., ¯u

(3)), ¯u

App

(2), ¯u

(2), ...,

¯u

(2n

− 2) + 1), ¯u

(2n

− 2) + 2), ... ,

¯u

(2n

− 1)), ¯u

App

), ¯u

)], if n

and U

,MN

= [ ¯u

(1), ¯u

(2), ..., ¯u

(1)),

¯u

App

(1), ¯u

(2) + 1), ¯u

(2) + 2),

..., ¯u

(3)), ¯u

App

(2), ¯u

(2), ..., ¯u

App

¯u

), ¯u

(2n

− 2) + 1), ¯u

(2n

−

2) + 2), . .. , ¯u

(N + M)], if n

6= n

. The

control inputs for the second virtual leader as

,MN

= [ ¯u

(1), ¯u

(1) + 1), ¯u

(1) + 2),

..., ¯u

(2)), ¯u

App

(1), ¯u

(2), ¯u

(3) + 1),

¯u

(3) + 2), ..., ¯u

(4)), ¯u

App

(2), ¯u

(3), ...,

¯u

App

− 1), ¯u

), ¯u

(2n

− 1) + 1),

¯u

(2n

−1)+ 2), ..., ¯u

(N+M)], if n

= n

and U

,MN

= [ ¯u

(1), ¯u

(1) + 1), ¯u

(1) +

2), ... , ¯u

(2)), ¯u

App

(1), ¯u

(2), ¯u

(3) +

1), ¯u

(3) + 2), ..., ¯u

(4)), ¯u

App

(2), ¯u

(3),

..., ¯u

(2n

− 1) + 1), ¯u

(2n

− 1) + 2),

..., ¯u

(2n

)), ¯u

App

− 1), ¯u

)], if

u ( )1

u ( )2

App

u ( )1

u ( )5

ψ (1)

Ψ (2)

ψ (4)

ψ (5)

(a) Trajectory of the ﬁrst vir-

tual leader.

u ( )3

u ( )4

ψ (2)

ψ (3)

ψ (4)

u (2)

u ( )1

App

u ( )1

(b) Trajectory of the second

virtual leader.

Figure 2: Trajectories with denoted control inputs and states

of the two virtual leaders. The solid black curves denote

trajectories where the virtual leader is leading the formation

while the gray curves denote trajectories where the virtual

leader is the virtual follower. The initial positions of the

leaders are depicted by gray shadows.

6= n

The value n

(resp. n

) is number of time in-

tervals in which the ﬁrst (resp. the second) virtual

leader has the leadership. Control inputs ¯u

( j),∀ j ∈

{1,...,n

} (resp. ¯u

( j),∀ j ∈ {1,...,n

}) are ob-

tained by the formation driving method when the ﬁrst

(resp. the second) virtual leader is the virtual follower.

The control inputs ¯u

App

( j),∀ j ∈ {1,...,n

} (resp.

¯u

App

( j),∀ j ∈ {1, . ..,n

− 1}) are applied for the

formation driving in the appendixes and are obtained

using K

App

and v

max,L

The vectors T

∆

,MN

(resp. T

∆

,MN

) will be com-

piled similar as the vector U

,MN

(resp. U

,MN

because the variables ¯u(·) and ∆t(·) are inseparably

joined. An example illustrating this approach is pre-

sented in Figure 2 where the parameters and outputs

of the optimization are: N = 0, M = 5, I

∈ {2,4},

= [ ¯u

(1), ¯u

(2), ¯u

App

(1), ¯u

(5)], U

[ ¯u

(1), ¯u

(3), ¯u

(4), ¯u

App

(1), ¯u

(2)].

The trajectory planning and the static as well as

dynamic obstacle avoidance problem for both virtual

leaders can be transformed to the minimization of sin-

gle cost function subject to sets of equality and in-

equality constraints. Accordingly the leader-follower

concept, the trajectory computed as the result of this

minimization will be used as an input of the trajec-

tory tracking for the followers. Details of the descrip-

tion of both, the leader trajectory planning and the

trajectory tracking for followers, can be found in our

previous publication in (Saska et al., 2009), where a

method with one leader enabling only forward move-

ment is presented.

4 EXPERIMENTAL RESULTS

The results presented in this section have been ob-

tained using the introduced algorithm with parame-

ters: n = 2, N = 4, M = 8, and ∆t = 0.25s. In the

scenario of a road with obstacles in Figure 3 a for-

mation of 6 robots is aimed to reach the target region

in minimum time. In accordance with real applica-

tion, the maximum forward and backward velocities

of the virtual leader of the formation were set unsym-

metrically as v

min,L

= −v

max,L

/2. Putting the ﬁnal re-

gion sufﬁciently far behind the formation, the solu-

tion of the formation to target zone problem is to turn

the formation and then continue forward to reach the

desired area. Such a maneuver, which contains two

switching between the virtual leaders, is denoted by

dashed curves in Figure 3(a). The solution of the task

keeps the formation outside the obstacles during the

whole maneuver. Beyond this, the ability to avoid

dynamic obstacles with collision course detected by

rear sensors of the robots during the reverse driving is

demonstrated in the simulation (see snapshots in Fig-

ure 3(b) and in Figure 3(c)). The complete history of

the turning can be seen in Figure 3(d).

Actual time: 0

(a) Initial position of the formation with complete plan for

both virtual leaders denoted by the dash curve.

Actual time: 6

(b) Detection of movement

of one obstacle and conse-

quential reaction of the fol-

lowers.

Actual time: 7.5

fully passed by the obstacle

and they are going back to

their position in the forma-

tion.

Actual time: 15.75

(d) Accomplished task with denoted trajectories of the

robots.

Figure 3: Snapshots of turning 180 degrees in the environ-

ment with static as well as dynamic obstacles.

The presented simulations have shown only simple ex-

periments to demonstrate a basic behavior of the pre-

sented approach. More complicated scenarios prov-

ing the ability to avoid a damaged follower crossing

trajectories of neighbors, to utilize different shapes of

formations or to deal with local minima in a complex

environment cannot be offered due to space limitation

of this paper, but can be found in (Saska et al., 2009;

Saska et al., 2007).

t=0s

(a) Two indoor robots in

positions appropriate for

cooperative shoveling ma-

terials to the side.

t=17s

(b) Robots have changed

formation to a shape ap-

propriate for turning.

t=41s

is overtaking the leader-

ship.

t=73s

(d) The leading duties are

going back to the ﬁrst

robot.

t=98s

(e) The formation has ﬁn-

ished the turning maneu-

ver.

t=115s

(f) Robots are again ready

for shoveling.

Figure 4: Formation turning at the end of a blind corridor.

The presented hardware experiment is a part of

airport snowshoveling project using formations of au-

tonomous ploughs, which has been reported in (Saska

et al., 2008; Hess et al., 2009). Here, we applied the

approach presented in this paper for turning the for-

mation of snow ploughs at the end of cleaning run-

way. The experiment has been performed on G2Bot

robotic platform equipped with SICK laser range

ﬁnder (not utilized in the experiment) and odometry.

In a simpliﬁed version of the experiments (see

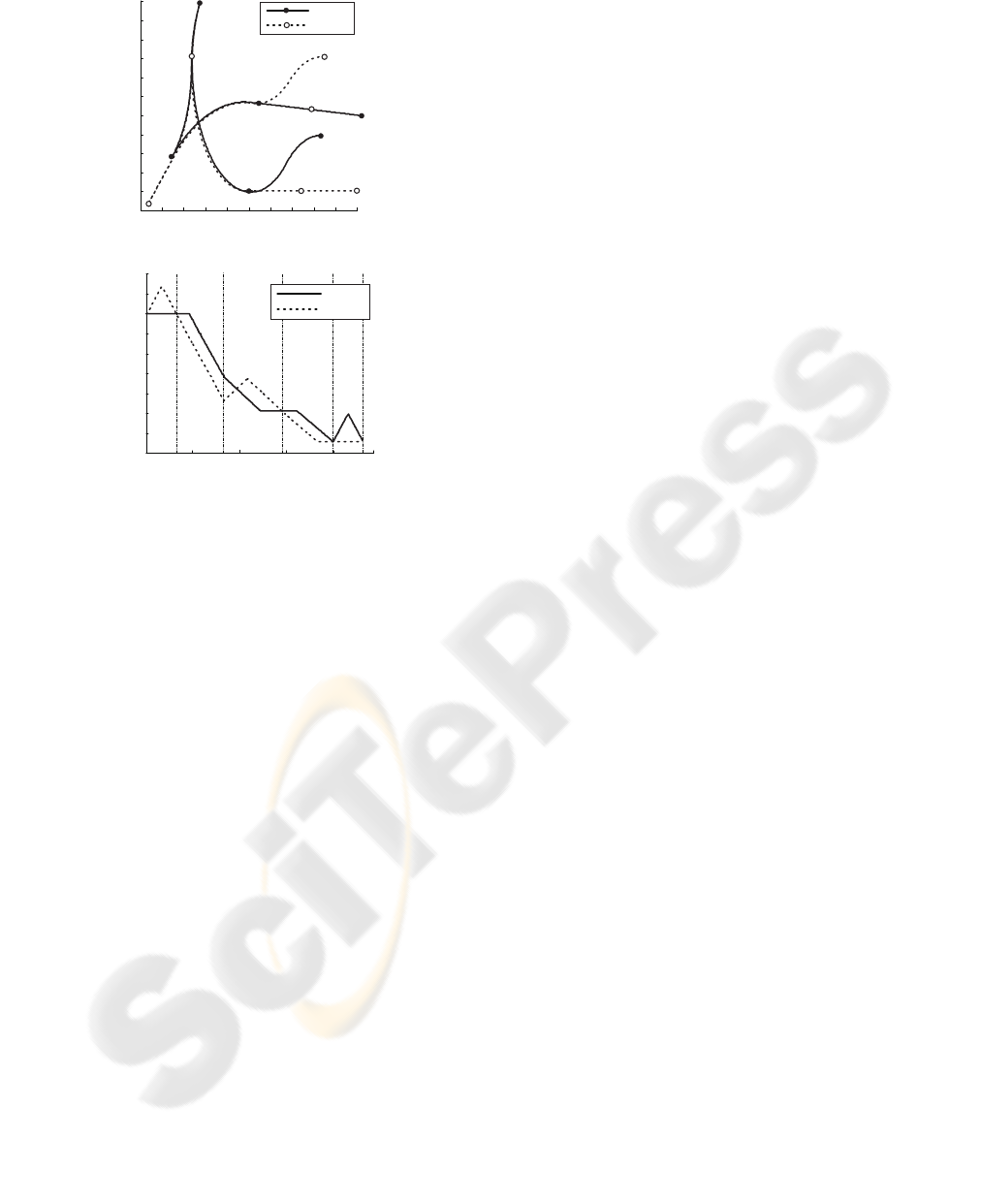
snapshots in Figure 4, data from odometry in Figure 5

and a movie of the experiment in (MOVIE, 2010)),

two autonomous indoor robots are facing a blind cor-

ridor with an aim to turn at the end. The map of the

environment and positions of the vehicles are known

before the mission. During the experiment, positions

are updated using a dead reckoning because an exter-

-5 -4.5 -4 -3.5 -3 -2.5 -2 -1.5 -1 -0.5 0

-0.2

0.2

0.4

0.6

0.8

1.2

1.4

1.6

1.8

t=115s

t=98s

t=115s

t=98s

t=0s

t=17s

t=41s

t=73s

Robot 1

Robot 2

x [m]

y [m]

(a)

25 50

100

-3.5

-3

-2.5

-2

-1.5

-1

-0.5

0.5

heading [rad]

time [s]

Robot 1

Robot 2

(b)

Figure 5: Data captured from odometry of both ploughs

with depicted times of snapshots in Figure 4.

nal positioning system is not necessary in such a short

term experiment. The actual position of robots and

their plans are shared via wireless communication.

The plan of robots is as follows: 1) build a compact

formation appropriate for turning, 2) turn 180 degrees

and 3) return back to the shoveling formation. Such

an approach is necessary in a case of largerformations

covering the whole runway and it can also better clar-

ify the method employing two virtual leaders. The

transitions between the different formations as well

as the turning maneuver are computed automatically

using the methods presented in this paper. Only the

positions of the vehicles within the formations (safety

distances, required overlapping of shovels etc.) are

given by experts.

5 CONCLUSIONS

In this paper, we have presented an RHC approach to

formation driving of car-like robots reaching a target

area in environments with obstacles. The proposed

approach is novel in the sense of utilized pair of com-

plementary virtual leaders necessary for guidance of

the formation during backward driving. This allows

us arbitrary maneuvers of formations including the U-

turn in bordered environment, which is necessary for

complete autonomous airport snow shoveling system.

The applicability of the presented approach has been

veriﬁed with simulations and hardware experiment.

ACKNOWLEDGEMENTS

This work is supported by the Czech Technical Uni-

versity under the grant SGS10/ 195/OHK3/ 2T/13

and by grants 2C06005 and MSM6840770038.

REFERENCES

Alamir, M. (2006). Stabilization of Nonlinear Systems Us-

ing Receding-Horizon Control Schemes, volume 339

of Lecture Notes in Control and Information Sciences.

Springer, Berlin / Heidelberg, Germany.

Barfoot, T. D. and Clark, C. M. (2004). Motion planning

for formations of mobile robots. Robotics and Au-

tonomous Systems, 46:65–78.

Dunbar, W. and Murray, R. (2006). Distributed receding

horizon control for multi-vehicle formation stabiliza-

tion. Automatica, 42(4):549–558.

Franco, E., Magni, L., Parisini, T., Polycarpou, M., and Rai-

mondo, D. (2008). Cooperative constrained control

of distributed agents with nonlinear dynamics and de-

layed information exchange: A stabilizing receding-

horizon approach. IEEE Transactions on Automatic

Control, 53(1):324–338.

Hess, M., Saska, M., and Schilling, K. (2009). Applica-

tion of coordinated multi vehicle formations for snow

shoveling on airports. Inteligent Service Robotics,

2(4):205 – 217.

Leitmann, G. (1980). Guaranteed avoidance strategies.

Journal of Optimization Theory and Applications,

32:569–576.

Mayne, D. Q., Rawlings, J. B., Rao, C. V., and Scokaert, P.

O. M. (2000). Constrained model predictive control:

Stability and optimality. Automatica, 36(6):789–814.

MOVIE (2010). Two indoor ploughs turning 360 degrees

[online]. [cit. 2010-1-13]. http://imr.felk.cvut.cz/ de-

mos/videos/ﬁles/shoveling.avi.

Saska, M., Ferenczi, I., Hess, M., and Schilling., K. (2007).

Path planning for formations using global optimiza-

tion with sparse grids. In In Proceedings of The 13th

IASTED International Conference on Robotics and

Applications (RA 2007)., Wuerzburg, Germany.

Saska, M., Hess, M., and Schilling, K. (2008). Efﬁ-

cient airport snow shoveling by applying autonomous

multi-vehicle formations. In Proceedings of IEEE In-

ternational Conference on Robotics and Automation,

Pasadena, USA.

Saska, M., Mejia, J. S., Stipanovic, D. M., and Schilling, K.

(2009). Control and navigation of formations of car-

like robots on a receding horizon. In Proc of 3rd IEEE

Multi-conference on Systems and Control.