ADAPTIVE FUZZY SLIDING MODE CONTROL FOR UNCERTAIN

NONLINEAR SYSTEMS AGAINST ACTUATOR FAULTS

Meriem Benbrahim, Najib Essounbouli, Abdelaziz Hamzaoui

CReSTIC, Reims University, 9 rue de Quebec B.P. 396, F-10026 Troyes Cedex, France

Ammar Betta

Batna University, 5 rue Chahid boukhlouf, 05000 Batna, Algeria

Keywords:

Fuzzy control, Fault tolerant control, Sliding mode control.

Abstract:

In this paper, we propose to combine the fuzzy sliding mode control to tolerate actuator faults of unknown

nonlinear systems subject to external disturbances. In particular, the idea of using adaptive fuzzy system to

tolerate actuator faults of unknown nonlinear systems by approximating the system functions and the effects

caused by actuator faults are avoided by the control structure. On the basis of Lyapunov stability theory its

shown that the resulting adaptive closed loop system can be guaranteed to be asymptotically stable in the

presence of faults on actuators and disturbances.

1 INTRODUCTION

In most practical control systems, components fail-

ures may occur at uncertain time and the size of

a fault is also unknown. The faults may lead to

performance deterioration or even instability of the

system. Therefore, the study of designing fault-

tolerant control (FTC) systems, which let the systems

operate in safe conditions and with proper perfor-

mances whenever components are healthy or faulted,

has received considerable attention over the past two

decades (Veillette, 1995) (Yang et al., 2001) (Wang.R

et al., 2007) (Liao.F et al., 2002) (Wu and Zhang,

2006) (Zhang et al., 2008) . The existing fault-tolerant

design approaches can be broadly classiﬁed into two

groups, namely passive approaches (Zhao and Jiang,

1998) and active approaches (Mao and Jiang, 2007).

In the passive approaches, robust control techniques

are utilized to design a ﬁxed controller for maintain-

ing the acceptable system stability and performances

throughout normal or faulty cases.

Recently, adaptivecontrol has been widely used to

deal with actuator faults in various systems. In (Tao

et al., 2004) (Boskovic et al., 1998), actuator lock-in-

place (stuck at some unknown place) failures were ac-

commodated by adaptive redundant control structure

for linear systems. (Tao et al., 2004) also contains

corresponding studies on some systems with known

nonlinearities. (Tang et al., 2007) extended the re-

sults to MIMO parametric-strict-feedback nonlinear

systems. Loss of actuator effectiveness is considered

in (Ye and Yang, 2006) (Yang and Ye, 2006) for linear

systems in the framework of linear matrix inequality

(LMI) to guarantee not only the stability, but also the

robust performance of the failed system. The com-

mon advantage of these adaptive control approaches

against actuator fault is that they are independent of

fault detection and diagnosis (FDD).

(Boskovic et al., 2005) (Boskovic and Mehra,

2006) developed adaptive ﬂight control based on mul-

tiple model, switching and tuning. However, the

methods mentioned above require that the controlled

system is known or only contains some linear un-

known parameters when there is on fault.

Since it was proved that adaptive fuzzy sys-

tems are universal approximators (Wang and Mendel,

1992), and stable adaptive fuzzy control design was

showed in (Wang, 1994), fuzzy logic systems (FLS)

and neural network (NN) have been used to nonlinear

systems, and also FTC systems. In (Polycarpou and

Helmicki, 1995), a general framework for construct-

ing automated fault diagnosis and accommodation ar-

chitectures was presented using on-line approxima-

tors and adaptive schemes, (Polycarpou et al., 2004)

(Zhang et al., 2004) (Zhang et al., 2006) (Mao et al.,

2006) (Xue and Jiang, 2006) provided several FTC

methods based on fuzzy logic systems (FLSs) or/and

NNs. (Diao and Passino, 2001) and (Rong et al.,

Benbrahim M., Essounbouli N., Hamzaoui A. and Betta A. (2010).

ADAPTIVE FUZZY SLIDING MODE CONTROL FOR UNCERTAIN NONLINEAR SYSTEMS AGAINST ACTUATOR FAULTS.

In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 92-97

 SciTePress

2006) applied FTC to practical systems for a turbine

engine and aircraft autolanding respectively. Most of

the existing works on fuzzy or neural networks FTC is

to detection and diagnosis/isolation faults with FLS or

NN. Thus, good fault detection and diagnosis (FDD)

is very important since if there are false or omitted

alarms of the faults, the overall system may even be-

come unstable. In (Ping and Yang, 2008), the au-

thors developed an adaptive FTC approach without

resorting to FDD mechanism to accommodate both

total and partial loss of effectiveness of actuators in

unknown afﬁne nonlinear systems. The main idea is

to introduce adaptive fuzzy systems to tolerate actua-

tor faults of unknown nonlinear systems by approxi-

mating the system functions and the effects caused by

actuator faults are avoided by the control structure.

However, using the projection algorithm need some

knowledge on the system behavior which represents a

restrictive assumption and increases the computation

time. Furthermore, only the free external disturbance

case is treated.

In this paper, we propose an adaptivefuzzy sliding

mode controller to tolerate actuator faults of unknown

nonlinear systems with external disturbances. In The

opposite case of the approaches developed in the lit-

erature, only one fuzzy system is used to approx-

imate the unknown dynamics, which allows avoid-

ing perfectly the controller singularity problem. Top

deal with the external disturbances and the approx-

imation errors, sliding mode technique is adopted.

Hence, the used sliding surface has been modiﬁed

such that the approaching phase is removed to over-

come the knowledge of the upper bound of distur-

bances to guarantee the sliding condition and to ef-

ﬁciently eliminate the chattering phenomenon.

This paper is organized as follows: Section 2 de-

scribes the problem statement. Section 3 is dedicated

to the synthesis of the proposed approach. In section4,

a simulation example demonstrates the effectiveness

of the propose scheme. Finally, section 5 concludes

the paper.

2 PROBLEM STATEMENT

Consider the following nonlinear system with m in-

puts:







˙x

= x

i+1

1 ≤ i ≤ n− 1

˙x

= f(x) + g

(x)u+ d(t)

y = x

(1)

where x = [x

, x

, ...,x

]

represents the state vec-

tor, u = [u

, ....,u

]

∈ ℜ

is the input vector whose

the component may fail during the system operation,

y ∈ ℜ is the output system, g

(x) = [g

, ....,g

] ∈ ℜ

and f(x) are unknown continuous nonlinear func-

tions. d is the bounded external disturbance. The

states x

(i = 1, ..., n) are measurable and the reference

output y

is bounded and sufﬁciently derivable. this

is a multiple input single output system with all the in-

puts contributed to a common control object like sta-

bilizing the closed loop system, tracking a reference

signal with satisfactory performance of both. There

are many such systems in our real life. The provided

approach is also effective for multi input multi output

systems. We only consider a simple case to simplify

the presentation. The actuator faults considered in this

paper is the loss of effectiveness which is modeled as

follows:



(t) = ρ

(t) 1 ≤ i ≤ m

∈ [0, 1]

(2)

is the still effectiveproportion of the i

actuator

after losing some effectiveness. When ρ

= 1, the cor-

responding actuator is normal (without fault). With

the actuator fault (2), the input vector can be rewrit-

ten as:

u(t) = ρν(t) (3)

where ν(t) = [ν

, ...,ν

]

is the applied control

vector and ρ = diag(ρ

, ...,ρ

The control objective is to design a robust adaptive

fuzzy sliding mode control law for the system (1)

with the actuator fault (2) to ensure that all signals

are bounded in the closed loop and the output y(t)

can track the given reference signal y

(t) as closely

as possible despite the presence of uncertainties, ex-

ternal disturbances and actuator faults. From the fault

model (2), it is reasonable that there is at least one ac-

tuator still active for the control purpose. In this case,

we propose to use a proportional actuation structure

as follows (Ping and Yang, 2008):

ν(t) = b ν

(t) (4)

where b = [b

, ...,b

]

represents the matrix of pro-

portional actuation and ν

(t) the proposed robust

adaptive fuzzy sliding mode control law. Using equa-

tions (3) and (4), the system (1) will be described by:







˙x

= x

i+1

1 ≤ i ≤ n− 1

˙x

= f(x) + g

(x)ρbν

(t) + d(t)

y = x

(5)

For this, the following assumptions are needed:

Assumption 1. System (1) is constructed such that

despite the loss of actuator effectiveness according to

(2), the system still be forced.

Assumption 2. The external disturbance d(t) is as-

sumed to be bounded, i;e., there exists a positive un-

known constant χ such that: |d| < χ.

The proposed control scheme combines fuzzy

logic for approximation and sliding mode for robust-

ness to attain the control objectives.

3 PROPOSED APPROACH

3.1 Fuzzy Logic System

An fuzzy logic system (FLS) consists of four parts:

the knowledge base, the fuzziﬁer, the fuzzy inference

engine manipulating fuzzy rules, and the defuzziﬁer

(Wang, 1994). The knowledge base for the FLS com-

prises a collection of fuzzy IF-THEN rules. The

fuzziﬁer maps a real point in the input space (mea-

surement of the systems state) to a fuzzy set. In gen-

eral there are two possible choices of this mapping,

namely singleton or non-singleton. In this paper, we

use the singleton fuzziﬁer mapping. The fuzzy infer-

ence engine performs a mapping from fuzzy sets of

the input to fuzzy sets in the output space, based on

the fuzzy IF-THEN rules (in the fuzzy rule base) and

the compositional rule of inference. The defuzziﬁer

maps fuzzy sets in the output space to a crisp point

in this space; in this study we use the centre-average

defuzziﬁer mapping (Wang, 1994).

The output of a multi-input single-output FLS with

centre-average defuzziﬁer, product inference, and sin-

gleton fuzziﬁer are of the following form:

y(x) =

∑

i=1

∏

j=1

))

∑

i=1

∏

j=1

)

(6)

where µ

) represents the membership degree of the

input x

, y

the conclusion constant corresponding to

the i

h rule and m the number of used fuzzy rules.

The output of the FLS can be rewritten on the follow-

ing vectorial form (Wang, 1994):

y(x) = ψ

φ(x) (7)

where ψ = [y

, ...,y

]

represents the vec-

tor of the adjustable parameters and φ(x) =

[

∏

j=1

)

∑

i=1

∏

j=1

)

, ...,

∏

j=1

)

∑

i=1

∏

j=1

)

]

the regressor vec-

tor.

According to the universal approximation theorem

(Wang, 1994), there exists an optimal fuzzy system

in the form (5) such it approximates uniformally an

unknown continuous function h(x) on a compact set

for any approximation accuracy:

h(x) = ψ

∗T

φ(x) + ε (8)

where ε is a very small positive constant.

3.2 Sliding Mode Control

To attain the desired objectives, we propose to use a

sliding mode control. This choice is motivated by the

fact that sliding mode allows to maintain the tracking

performancesin presence of both structural uncertain-

ties and external disturbances (Slotine and Li, 1991).

For this, we consider the following sliding surface:

S(t) = e

(n−1)

(t) +

n−1

∑

i=1

i−1

(i−1)

(t) (9)

where e(t) = y

(t) − y(t) denotes the tracking er-

ror and e

(i)

(t) its i

time derivative. The constants λ

are chosen such the corresponding polynomial roots

are stable (Slotine and Li, 1991). Using the sliding

surface S(t) in this actual form presents two major

drawbacks: (i) during the reaching phase, the system

is sensitive to uncertainties and external disturbances,

which provokes chattering phenomenon in the neigh-

borhood of the sliding surface. (ii) Choosing big val-

ues of the slops which allows reducing the reaching

phase but requires an important starting energy, and

small values give a slow response. So, it is necessary

to ﬁnd a trade-off between the starting energy and the

time response (Hussain et al., 2010). To overcome

this problem, we propose to use a modiﬁed the slid-

ing surface allowing to suppress the reaching phase,

and hence the system will be at t = 0 on the surface

(S(t) = 0). In this case, the sliding surface will be

deﬁned as follows:

S(t) = e

(n−1)

(t) +

n−1

∑

i=1

i−1

(i−1)

(t)

−



− arctg(t)





(n−1)

n−1

∑

i=1

i−1

(i−1)



(0)

= e

(n−1)

(t) +

n−1

∑

i=1

i−1

(i−1)

(t) + S

(10)

If f (x) and [g

(x)ρb] are well known, the control

law can be given as:

= [g

(x)ρb]

−1



− f(x) + y

(n)

n−1

∑

i=1

i−1

(i)

(t)



+[g

(x)ρb]

−1

sign(S(t)]

(11)

Where k

is a positive constant chosen such that:

S(t).

S(t) < 0.

However, the dynamics of the system studied in

our paper are unknown which makes the use of this

control law impossible. To resolve this problem, one

can use direct adaptive fuzzy controller or an indirect

adaptive fuzzy controller. In the direct scheme, the

control law is approximated by a fuzzy system. How-

ever, the control gain must be constant or satisfying

some restrictive assumptions. The indirect scheme

consists in approximating the unknown dynamics by

two fuzzy systems to synthesize the control law. Nev-

ertheless, the used adaptation laws are very compli-

cated to avoid the singularity problem. In this work,

we propose to approximate the unknown terms using

only one fuzzy system under the constraint that the ro-

bustness of the closed loop system is guaranteed and

the number of the involved parameters in the control

design is reduced.

3.3 Control Law Synthesis

This section is dedicated to the synthesis of the pro-

posed approach.

Using (5), the time derivative of the sliding surface

(10) is given by:

S(t)= e

(n)

n−1

∑

i=1

i−1

(i)

(t)

S(t)= y

(n)

− f (x) − [g

(x)ρb]ν

− d +

n−1

∑

i=1

i−1

(i)

(t)

(12)

If we muster all the unknown parameters in one, the

above expression can be rewritten as:

S(t) = y

(n)

− f

(x) − [g

(x)ρb]ν

(13)

where f

(x) = f(x) + d −

n−1

∑

i=1

i−1

(i)

(t).

According to assumption 1, we have [g

(x)ρb] 6=

0. So, it can be positive or negative. We assume in

this work, that there exists a positive constant g

such

that: [g

(x)ρb] > g

> 0. Furthermore, the function

(x) is unknown. To attain the control objectives, we

propose to use a fuzzy system ψ

φ(x) to approximate.

We deﬁne a new variable α such that: α = g

−1

kψk

According to (8), and the approximation error as:

α =

α−

α whose time derivative is given by:

α = −

Proposition The control law

= M

.S(t) +

2β

φ(x)

φ(x)S(t) (14)

with

α =

2.β

φ(x)

φ(x)S(t) (15)

guarantees the stability and the robustness of the

closed loop system in presence of actuators faults.

It ensures also the boundedness of all the involved

signals.

Proof.

According to (8), (13) and (14), using the fact that the

reference signal y

(n)

yields to:

S(t)

S(t) ≤

2β

φ(x)

φ(x)S

(t) +

(t)

(ε

+χ

)

− [g

(x)ρb]ν

(16)

Where η and χ two positive constants.

To prove the stability, we consider the following Lya-

punov function:

(t) +

2β

(17)

Using equations (15) and (16), the time derivative of

(17) becomes:

≤

(ε

+χ

)

− g

σα

−2g

(t)

− g

ησ

(18)

Let a

(ε

+χ

)

− g

σα

and b

min(2g

, ησ). Then, the time derivative of V

given by:

≤ a

+ b

(0) (19)

which implies

(t) ≤ V

(0)exp(a

t) +

∀t ≥ 0

(20)

Hence, the Lyapunov function converges toward a

bounded value

. This implies that all the involved

signals are bounded. Furthermore, we can have

lim

t→∞

S(t) ≤ 2

, which ensures the convergence of the

tracking error to zero (Wang, 1994).

4 SIMULATION AND RESULTS

In this section, the presented adaptive fuzzy fault

tolerant controller is applied to a nonlinear system

with the actuator faults described as (2).

Example: We consider that after transformation,

the nonlinear system can be written as the following

form which has a redundancy actuation structure.

˙x

= x

˙x

5sinx

−0.02x

cos(x

)sin(x

)

3−0.2cos

cos

3−0.2cos

2cos

3−0.2cos

+ d

(21)

Where the actuators of u

and u

are the con-

trol inputs, d = 0.1sin(2t) represents the external dis-

turbance. The evolution of the actuators effective-

ness ρ = diag(ρ

, ρ

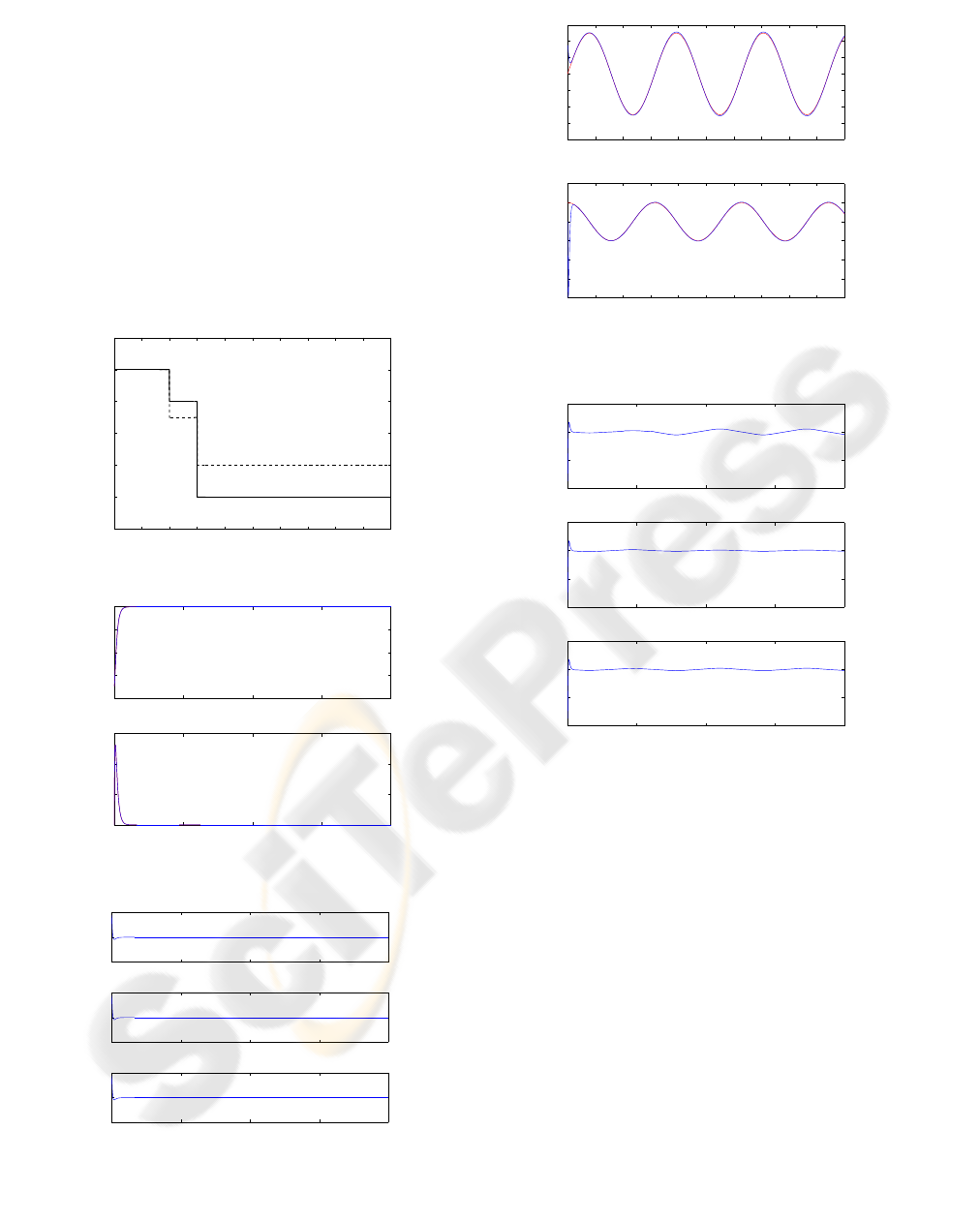
) is given by ﬁgure (1). In or-

der to control system (21), the proposed control law

is applied with the following simulation parameters:

m = 5× 5 = 25 rules for the fuzzy logic system, with

ρ = 0.01, γ = 4.250 and initial values α = 0

. Fig-

ures 2 and 3 give the simulation results for regula-

tion problem and 4-5 those of tracking of a sinusoidal

reference signal. We can see the convergence of the

states to their respective reference signals despite the

presence of both effectiveness loss (ﬁgure 1) and ex-

ternal disturbances.

0 2 4 6 8 10 12 14 16 18 20

0.2

0.4

0.6

0.8

Time (s)

Figure 1: Evolution of the effectiveness: (–): ρ

, (- -): ρ

0 5 10 15 20

−0.4

−0.3

−0.2

−0.1

Time(s)

y(t)

0 5 10 15 20

0.5

1.5

Time(s)

dy(t)/dt

Figure 2: Evolution of the state variables.

0 5 10 15 20

−100

100

Time(s)

Applied control v

0 5 10 15 20

−50

Time(s)

0 5 10 15 20

−50

Time(s)

Figure 3: Control signals.

0 2 4 6 8 10 12 14 16 18 20

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

Time(s)

y(t)

0 2 4 6 8 10 12 14 16 18 20

−2

−1.5

−1

−0.5

0.5

Time(s)

dy(t)/dt

Figure 4: Evolution of the state variables and their reference

signals.

0 5 10 15 20

−200

−100

100

Applied control v

Time(s)

0 5 10 15 20

−100

−50

Time(s)

0 5 10 15 20

−100

−50

Time(s)

Figure 5: Control signals: ν u

and u

5 CONCLUSIONS

In this paper, a fuzzy sliding mode approach of fault

tolerant control problem for an uncertain perturbed

nonlinear system is studied. To overcomethe problem

of unknown dynamics, only one adaptive fuzzy sys-

tem has been used. Furthermore, the sliding surface

has been modiﬁed to suppress the reaching phase and

hence improve the robustness of the closed loop sys-

tem. The global stability has been established in the

sense of Lyapunov. Many simulations have presented

to show the good performances despite the presence

of actuator failures. As future work, the case of actu-

ator lock-in-place will be also treated and the exten-

sion of this approach to multi-input multi-output will

be studied.

ACKNOWLEDGEMENTS

This work is developedfor the project CPER-MOSYP

and supported by both the Champagne-Adrdenne Re-

gion and the European found FEDER.

REFERENCES

Boskovic, J., Bergstrom, S., and Mehra, R. (2005). Adap-

tive accommodation of failures in second-order ﬂight

control actuators with measurable rates. In American

Control Conference.

Boskovic, J. and Mehra, R. (2006). A multiple model-based

decentralized system for accommodation of failures

in second-order ﬂight control actuators. In American

Control Conference.

Boskovic, J., Yu, S., and Mehra, R. (1998). A stable scheme

for automatic control reconﬁguration in the presence

of actuator failures. In American Control Conference.

New york:IEEE Press.

Diao, Y. and Passino, K. (2001). Stable fault-tolerant adap-

tive fuzzy/neural control for a turbine engine. IEEE

Transactions on Control Systems Technology.

Hussain, A., Essounbouli, N., and Hamzaoui, A. (2010).

A robust adaptive fuzzy wavelet network based con-

troller for a class of nonlinear systems. American Con-

trol Conference Westin Seattle Hotel, Seattle, Wash-

ington, USA.

Liao.F, .Wang, J., and Yang, G. (2002). Reliable robust

ﬂight tracking control: an lmi approach. IEEE Trans-

actions on Control Systems Technology.

Mao, Z. and Jiang, B. (2007). Fault estimation and accom-

modation for networked control systems with transfer

delay. Acta Automatica Sinica.

Mao, Z., Jiang, B., and Chowdhury, F. (2006). Fault ac-

commodation for a class of nonlinear ﬂilght control

systems. International Symposium on Systems and

Control in Aerospace and Astronautics.

Ping, L. and Yang, G.-H. (2008). Fault tolerant control for

unknown nonlinear systems with actuator failures: An

adaptive fuzzy approach. American Control Confer-

ence Westin Seattle Hotel, Seattle, Washington, USA.

Polycarpou, M. and Helmicki, A. (1995). Automated fault

detection and accommodation: a learning systems ap-

proach. IEEE Transactions on Systems, Man, and Cy-

bernetics.

Polycarpou, M., Zhang, X., Xu, R., Yang, Y., and Kwan, C.

(2004). A neural network based approach to adaptive

fault tolerant ﬂight control. In TEMPLATE’06, 1st In-

ternational Conference on Template Production.

Rong, H. J., Huang, G. B., Sundararajan, N., and Saratchan-

dran, P. (2006). Fuzzy fault tolerant controller for ac-

tuator failures during aircraft autolanding. IEEE In-

ternational Conference on fuzzy systems.

Slotine, J. and Li, W. (1991). Applied Nonlinear Control.

Englewood Cliffs Prentice Hall, New Jersey.

Tang, X., Tao, G., and Joshi, S. (2007). Adaptive actua-

tor failure compensation for nonlinear mimo systems

with an aircraft control application. Automatica.

Tao, G., Chen, S., Tang, X., and al (2004). Adaptive Control

of Systems with Actuator Failures. Springer-Verlag,

Berlin.

Veillette, R. (1995). Reliable linear-quadratic state-

feedback control. Automatica.

Wang, L. (1994). Adaptive fuzzy systems and control. En-

glewood Cliffs NJ: Prentice Hall, New Jersey.

Wang, L. and Mendel, J. (1992). Fuzzy basis functions,

universal approximation, and orthogonal least-squares

learning. IEEE Transactions on Neural Networks.

Wang.R, Jin, G., and Zhao, J. (2007). Robust fault-tolerant

control for a class of switched nonlinear systems in

lower triangular form. Asian Journal of Control.

Wu, H. and Zhang, H. (2006). Reliable hinf fuzzy control

for continuous-time nonlinear systems with actuator

failures. IEEE Transactions on Fuzzy Systems.

Xue, H. and Jiang, J. (2006). Fault detection and accommo-

dation for nonlinear systems using fuzzy neural net-

works. IEEE 5th International Power Electronics and

Motion Control Conference.

Yang, G., Wang, J., and Soh, Y. (2001). Reliable hinf con-

troller design for linear systems. Automatica.

Yang, G. and Ye, D. (2006). Adaptive fault-tolerant hinf

control via state feedback for linear systems against

actuator faults. In 45th IEEE Conference on Decision

and Control.

Ye, D. and Yang, G. (2006). Adaptive fault-tolerant track-

ing control against actuator faults with application to

ﬂight control. IEEE Transactions on Control Systems

Technology.

Zhang, D., Wang, Z., and Hu, S. (2008). Robust satisfac-

tory fault tolerant control of uncertain linear discrete-

time systems:an lmi approach. International Journal

of Systems Science.

Zhang, X., Liu, Y., Rysdyk, R., Kwan, C., and Xu, R.

(2006). An intelligent hierarchical approach to ac-

tuator fault diagnosis and accommodation. IEEE

Aerospace Conference.

Zhang, X. D., Parisini, T., and Polycarpou, M. M. (2004).

Adaptive fault-tolerant control of nonlinear uncertain

systems: an information-based diagnostic approach.

IEEE Transactions on Automatic Control.

Zhao, Q. and Jiang, J. (1998). Reliable state feedback con-

trol system design against actuator failures. Automat-

ica.