MORPHING WING REAL TIME OPTIMIZATION

IN WIND TUNNEL TESTS

Andrei V. Popov, Lucian T. Grigorie, Ruxandra Botez

École de Technologie Supérieure, Montréal, Québec, H3C 1K3, Canada

Mahmoud Mamou, Youssef Mébarki

Institute for Aerospace Research, NRC, Ottawa, Ontario, K1A 0R6, Canada

Keywords: Morphing Wing, Real Time Optimization, Wind Tunnel, Laminar-to-turbulence Transition.

Abstract: In this paper, wind tunnel results of a real time optimization of a morphing wing in wind tunnel for delaying

the transition towards the trailing edge are presented. A morphing rectangular finite aspect ratio wing,

having a wind tunnel experimental airfoil reference cross-section, was considered with its upper surface

made of a flexible composite material and instrumented with Kulite pressure sensors, and two smart

memory alloys actuators. Several wind tunnel tests runs for various Mach numbers, angles of attack and

Reynolds numbers were performed in the 6’×9’ wind tunnel at the Institute for Aerospace Research at the

National Research Council Canada. Unsteady pressure signals were recorded and used as feed back in real

time control while the morphing wing was requested to reproduce various optimized airfoils by changing

automatically the two actuators strokes. The paper shows the optimization method implemented into the

control software code that allows the morphing wing to adjust its shape to an optimum configuration under

the wind tunnel airflow conditions.

1 INTRODUCTION

The Consortium for Research and Innovation in

Aerospace in Quebec CRIAQ 7.1 project was a

collaborative project between the teams from École

de technologie superieure (ETS), École

Polytechnique, the Institute for Aerospace Research

- National Research Canada (IAR-NRC),

Bombardier Aerospace, Thales Avionics. In this

project, the laminar flow past aerodynamically

morphing wing was improved in order to obtain

important drag reductions.

This collaboration called for both aerodynamic

modeling as well as conceptual demonstration of the

morphing principle on real models placed inside the

wind tunnel. Drag reduction on a wing could be

achieved by modifications of the airfoil shape which

had an effect in the laminar to turbulent flow

transition point position. The main objective of this

concept was to promote large laminar regions on the

wing surface by moving the transition point toward

the trailing edge of the airfoil wing, thus reducing

drag over an operating range of flow conditions

characterized by Mach numbers, airspeeds and

angles of attack (Zingg, 2006).

To modify the laminar flow around a wing

airfoil, it was necessary to change the airfoil shape;

therefore one of the methods for airfoil changes was

developed at Kentucky University, which consisted

of deflecting the wing upper surface using adaptive

actuators (Jacob and Munday, 1998, 1999, 2002).

It was shown that the actuators activated

oscillatory motions of a certain frequency to the

boundary layer flow over the upper surface. These

actuators were made of piezo-electric materials

which changed their shapes when connected to an

electrical current differential voltage. The wind

tunnel tests showed that the displacement of the

transition point to the trailing edge resulted in the

drag decrease and in the lift increase (Jacob, 1999).

The “chordwise air collection” method was

designed in 1984, in fact, laminar flow control

(LFC) over the upper surface of the wing was

realized by the boundary layer suction, thereby

moving the transition position at 85% of the chord

(Allison, 1978).

114

V. Popov A., T. Grigorie L., Botez R., Mamou M. and M

ebarki Y. (2010).

MORPHING WING REAL TIME OPTIMIZATION IN WIND TUNNEL TESTS.

In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 114-124

 SciTePress

A numerical algorithm was developed for

optimizing the suction distribution, by maintaining

the transition at a desired location (chord %) and

maintaining the energy spent at a minimum

(Hackenberg, 1995). Three steps were considered: 1.

Boundary layer computation; 2. Transition

prediction, and 3. Optimization of the suction

distribution while maintaining the transition location

at a certain desired percentage of the chord. In the

third step, the gradient method was used.

Optimized wings were conceived by reducing the

kinetic energy of the perturbation and drag values

while, the lift and pitch moment coefficients were

maintained at desired values (Pralits, 2003).

A controller was developed at Southampton

University, with the aim of maintaining the desired

turbulence level over a flat plate equipped with a

suction porous panel. The pressure fluctuations were

measured with microphones at the boundary layer

over the flat plate, and the signal was conditioned

and filtered to remove the background noise of the

wind tunnel fan, then the turbulence level was

estimated by computing the RMS (Root Mean

Square) pressure signal. The controller used the

error between the RMS values of the measured

pressures and the desired RMS values at the spots

where the microphones were installed, thus

maintaining the transition on the specified area over

the flat plate (Rioual, 1994).

Closed-loop control of the morphing planform

(wing-shape control) and simultaneously enforced

prescribed closed loop aircraft dynamics (flight

control) were modeled (Gandhi, 2007). The N-MAS

wing designed by NextGen Aeronautics was

considered. The flight control law actively used the

leading edge morphing wing sweep angle as an

actuator to assist in manoeuvres while guaranteeing

aircraft stability. The morph between the two modes

of Loiter and Dash was modeled by a first-order

transfer function, and hence the morph rate was

governed by the transfer function time constant.

The empirical structural weights for various wing

geometries were obtained by implementing two

finite element-based structural optimization

methods: 1) an aggregate and 2) a simultaneous

analysis (Skillen, 2005). These methods were

applied on a morphing wing with two degrees of

freedom: the wing sweep and the root chord length.

Two linear actuators were used: one positioned

along and parallel to the forward spar and the other

one positioned along and parallel to the wing root

chord. These geometrical variations produced four

configurations with changes in area, aspect ratio and

sweep: the high lift configuration for the largest area

and minimal sweep angle; the loiter configuration

for the maximum aspect ratio and minimum sweep

angle; the dash/cruise configuration for the

maximum sweep and minimal area; and the

manoeuvre configuration for the maximum area at

the maximum sweep.

A symmetric wing structure was created with

two tapered graphite/epoxy composite plates and a

steel body. Four pairs of SMA wires were attached

to the wings’ bottom surfaces in the chord-wise

direction. Lift and drag forces were measured at

various angles of attack. Dynamic vibration signals

were measured by Fiber Bragg Grating FBG sensors

at the wing root and were used to monitor aeroelastic

unstable flutter phenomena, at various angles of

attack (Yang, 2006).

A wing structure comprised of an optimized

internal layout of cables and struts was able to

change its shape. Cables were used as actuators,

while struts provided rigidity to the wing. In addition

to achieving continuous morphing by changing cable

lengths, this structure had the advantages of being

light weighted and having a distributed actuation.

Topology optimization was used to optimally place

cables and struts in a bay or in a wing section. The

Non-dominated Sorting Genetic Algorithm II

(NSGA II) was used for modeling the NASA HECS

and the NextGen TSCh wings (Bharti, 2006).

Wings roll performances were achieved by use

of articulated conformal control surfaces. Analysis

results were compared to experimental results

obtained for a 16% scale model of a fighter wing

equipped with embedded smart materials used to

deform a control surface. The control surface design

was found suitable for low-rate applications such as

takeoff and landing configurations (Sanders, 2003).

NextGen developed an in-plane morphing geometry

concept. Flexible elastomeric skins with out-of-

plane stiffeners accommodated the wing motion

while transmitting air pressure loads to the wing

substructure. Wind tunnel testing of a full-scale

wing for a 2400 lb vehicle and flight testing of a

subscale unmanned aerial vehicle (UAV) were

performed. The following issues were identified: the

need to address multiple geometries and flight

envelopes to account for morphing shape changes;

the in-plane wing flexibility resulting from its

mechanism restraint by linear actuators. Another

half-span wind tunnel model was tested in the

NASA Transonic Dynamics Tunnel for

aeroelasticity studies (Andersen, 2007).

The Flight Test results of a Mission Adaptive

Compliant Wing (MAC-Wing) variable geometry

Trailing Edge Flap with a Natural Laminar Flow

NLF airfoil have been described. The MAC-Wing

technology provided light-weight, low power,

MORPHING WING REAL TIME OPTIMIZATION IN WIND TUNNEL TESTS

115

variable geometry reshaping of the upper and lower

flap surface with no discontinuities. The airfoil-flap

system was optimized to maximize the laminar

boundary layer extent over a broad lift coefficient

range for endurance aircraft applications. The

expanded laminar bucket capability allowed the

endurance aircraft to extend their range, by 15% or

more, by optimizing the lift-to-drag ratio (L/D)

throughout the mission. The wing was tested at full-

scale dynamic pressure, Mach number, and reduced-

scale Reynolds numbers on Scaled Composites’

Knight Aircraft. Laminar flow regime occurred up to

60% chord of the wing during tests. Significant fuel

and weight savings as well as high control authority

were verified by tests and analyses. Fifteen Dantec

Dynamics hot film sensors measured the boundary

layer transition position (De Breuker, 2007).

A Defense Advances Research Projects Agency

DARPA sponsored wind tunnel test model of a

Lockheed Martin morphing concept was designed

and tested. The wind tunnel model incorporated the

key features representatives of a full scale vehicle

model: out-of-plane morphing through a coordinated

actuation system integrated with seamless skins and

a composite support structure that encompassed the

actuator system along the wing fold hinge lines,

structural layout and materials featured in the full

scale vehicle design, and a first-time thermo-

polymer actuator integral to a leading edge device

for smooth contour between the inner wing and

fuselage when fully morphed. The model was

instrumented with strain gauges, accelerometers and

pressure transducers; data was acquired and

correlated with aircraft design and analysis methods

(Love, 2007).

The airborne modification of an aircraft wing

airfoil shape could be realized continuously to

maintain laminar flow over the wing surface as

flight conditions changed. To achieve such a full

operating concept, a closed loop control system

concept was developed to control the flow

fluctuations over the wing surface with the

deformation mechanisms (actuators) (Popov, 2008).

The wing model had a rectangular plan form of

aspect ratio of 2 and was equipped with a flexible

upper surface skin on which shape memory alloys

actuators were installed (Coutu, 2009 and Georges,

2009). Two shape memory alloys (SMA) actuators

created the displacement of the two control points on

the flexible skin in order to realize the optimized

airfoil shapes (Sainmont, 2009).

As reference airfoil, the laminar Wind Tunnel

Experimental Airfoil WTEA was used because it

was already optimized for laminar flow in the

transonic regime; its aerodynamic performance was

investigated at IAR-NRC (Khalid, 1993). The

optimized airfoils were previously calculated by

modifying the reference airfoil for each airflow

condition as combinations of angles of attack and

Mach numbers such that the transition point position

was found to be the nearest as possible to the airfoil

trailing edge (Sainmont, 2009). Several optimized

airfoils were found for the airflow cases

combinations of Mach numbers and angles of attack.

The optimized airfoils configurations were stored in

the computer memory by means of a database and

were selected as needed by the operator or computer

in order to be realized by the morphing wing

(Popov, 2009). But this strategy relied on the

previously calculated aerodynamic characteristics of

the airfoils which usually were determined by use of

CFD codes and optimization algorithms.

The idea presented in this paper was to

implement the same optimization algorithm into the

computer controller that would search the optimal

configuration with the real system, in real time and

for real aerodynamic airflow conditions. The basic

idea of optimization control is to by-pass the

necessity of a previously calculated optimized

airfoils database, and to generate in real time the

optimized airfoil for the exact conditions of the wind

flow. For such a task it was necessary to develop a

subroutine that optimized the airfoil shape in the

same way in which the optimized airfoils database

was generated. The method of optimization used in

this case was a mixed method between ‘the gradient

ascent’ or ‘hill climbing’ method and the ‘simulated

annealing’ which is a meta-heuristic search method.

The ‘hill climbing’ method is a local search

optimization algorithm. It considers a random poor

solution, which improves slowly by iterations. When

solution cannot be further improved, it becomes the

final solution and the algorithm ends. In our case,

the searching domain is defined by the actuators

displacements as variables, while the cost function

needed to be maximized is the transition point

position x

. Normally the function is defined

analytically and the maximum is searched along the

lines with the maximum local derivatives or

gradients. Although ‘hill climbing’ would be very

fast and simple to program, the solution found is not

guaranteed to be the global maximum of the entire

search domain (Hill climbing, from Wikipedia).

Other local search algorithms such as ‘stochastic hill

climbing’, ‘random walks’ and ‘simulated

annealing’ would overcome this problem. The

characteristic of these methods is that the algorithm

searches random solutions within the search domain

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

116

in order to cover all the possible local maxima and

to find the global maximum (Simulated annealing,

from Wikipedia).

The reason why a mixed method was needed,

was because the cost function for such complex

problem (minimize the CD, maximize the CL/CD or

maximize the transition point position xtr for a

morphing wing) was not defined analytically and the

implementation of ‘gradient ascent’ method was not

suitable. Also, due to time cost (very long time

response of the SMA actuators due to heating but

especially cooling time), a purely probabilistic meta-

heuristic search algorithm such as ‘stochastic hill

climbing’, ‘random walks’ and ‘simulated

annealing’, was not suitable too.

The idea of the present algorithm was the

mixture of the ‘hill climbing’ method with the

‘random walks’ or ‘simulated annealing’ and the

search within the defined domain nine points, one

being the center of a circle while the other eight

being situated on the circle with a predefined radius.

When the maximum is found within the nine points,

the algorithm reset the next searching step by

iterating with eight points situated on smaller circles

until the global maximum is found. This mixed

method was found to be the fastest i.e. it considered

the least number of points evaluated for converging

to the transition point position x

maximum.

2 EXPERIMENTAL SETUP

DESCRIPTION

2.1 Mechanical and Electrical Control

System

The concept of this morphing wing consisted in a

rectangular wing model (chord c = 0.5 m and span b

= 2.1 m) incorporating two parts. One fixed part was

built in aluminum by the IAR-NRC team which

sustained the resistance forces acting during wind

tunnel tests. The other part consisted in a flexible

skin installed on a metallic structure on the wing

upper surface and was designed and manufactured at

Ecole de Technologie Superieure (Fig. 1). The

flexible skin was required to change its shape

through two action points in order to realize the

optimized airfoil for the airflow conditions in which

tests were performed.

The actuators were composed of two oblique

cams sliding rods span-wise positioned that

converted the horizontal movement along the span in

vertical motion perpendicular to the chord (Fig. 2).

Figure 1: Cross section of the morphing wing model.

The position of each actuator was given by the

mechanical equilibrium between the Ni-Ti alloy

SMA wires that pulled the sliding rod in one

direction and the gas springs that pulled the sliding

rod in the reverse direction. The gas springs role was

to counteract the pulling effect of aerodynamic

forces acting in wind tunnel over the flexible skin

when the SMA’s were inactive. Each sliding rod was

actuated by means of three parallel SMA wires

connected to a current controllable power supply

which was the equivalent of six wires acting

together. The pulling action of the gas spring

retracted the flexible skin in the undeformed-

reference airfoil position, while the pulling action of

the SMA wires deployed the actuators in the load

mode i.e. morphed airfoil in the optimized airfoil

position (see Fig. 2). The gas springs used for these

tests were charged with an initial load of 225 lbf

(1000 N) and had a characteristic rigidity of 16.8 lbf

/ in (2.96 N / mm).

Figure 2: Schematics of the flexible skin mechanical

actuation.

The mechanical SMA actuators system was

controlled electrically through an “open loop”

control system. The architecture of the wing model

open loop control system, SMA actuators and

controller is shown in Figure 3. The two SMA

actuators had six wires each, which were supplied

with power by the two AMREL SPS power supplies,

controlled through analog signals by the NI-DAQ

USB 6229 data acquisition card. The NI-DAQ was

connected to a laptop through an USB connection. A

control program was implemented in Simulink

which provided to the power supplies the needed

SMA current values through an analog signal as

flexible skin

spring

SMA

actuator

rod

roller

cam

First

actuating line

Second

actuating line

MORPHING WING REAL TIME OPTIMIZATION IN WIND TUNNEL TESTS

117

shown in Figure 3. The control signal of 2 V

corresponded to an SMA supplied current of 33 A.

The Simulink control program used as feedback

three temperature signals coming from three

thermocouples installed on each wire of the SMA

actuator, and a position signal from a linear variable

differential transducer (LVDT) connected to the

oblique cam sliding rod of each actuator. The

temperature signals served in the overheat protection

system that disconnected the current supply to the

SMA in case of wire temperature passed over the set

limit of 120°C. The position signals served as

feedback for the actuator desired position control.

The oblique cam sliding rod had a horizontal versus

vertical ratio 3:1; hence the maximum horizontal

displacement of the sliding rod by 24 mm was

converted into a maximum vertical displacement of

the actuator and implicit of the flexible skin by 8

mm.

Figure 3: Architecture of the morphing wing model

control system.

A user interface was implemented in

Matlab/Simulink which allowed the user to choose

the optimized airfoils shape from database stored on

the computer hard disk and provided to the

controller the vertical needed displacements in order

to obtain the desired optimized airfoil shape. The

controller activated the power supplies with the

needed SMA current values through an analog signal

as shown in Figure 3. In practice, the SMA wires

were heated at an approximate temperature of 90°C

with a current of 10 A. When the actuator reached

the desired position the current was shut off and the

SMA was cycled in endless heating/cooling cycles

through the controller switching command on/off of

the current in order to maintain the current position

until another desired position or the entire system

shut off was required.

In support of the discrete pressure

instrumentation, infrared thermography (IR)

visualization was performed to detect the transition

location on the morphing wing upper surface and

validate the pressure sensor analysis. The transition

detection method using IR was based on the

differences in laminar and turbulent convective heat

transfer coefficient and was exacerbated by the

artificial increase of model-air flow temperature

differences. In the resulting images, the sharp

temperature gradient separating high temperature

(white intensity in image) and low temperature (dark

intensity) regions was an indication of the transition

location. The infrared camera used was an Agema

SC3000 camera, equipped with a 240×320 pixels

Quantum Well Infrared Photodetector (QWIP

detector), operating in the infrared wavelength

region of 8-9 µm and cooled to 70°K to reduce

thermal noise. The camera provided a resolution of

0.02ºC and a maximum frame rate of 60 Hz. It was

equipped with the default lens (FOV = 20°×15°),

and was installed 1.5 m away from the model with

an optical axis oriented in the horizontal plane at

about 30° with respect to the wing surface mid-

chord normal. Optical access was provided through

an opening on the side wall of the test section

opposite to the upper surface. More details about the

methodology and processing are available in ref.

(Mébarki, 2009).

2.2 Aerodynamic Detection System and

Graphical User Interface

The morphing wing goal was the improvement of

the laminar flow over the upper surface of the wing.

In order to ensure that the improvement was real, we

built a detection system that gave information about

the flow characteristics. An array of twelve Kulite

pressure sensors was installed on the flexible skin.

The pressure data acquisition was performed

using a NI-DAQ USB 6210 card with 16 analog

inputs, at a total sampling rate of 250 kilo samples/s.

The input channels were connected directly to the

IAR-NRC analog data acquisition system which was

connected to the twelve Kulite sensors. The IAR-

NRC served as an amplifier and conditioner of the

signal at a sampling rate of 15 kilo samples/s. One

extra channel was used for the wind tunnel dynamic

pressure acquisition to calculate the pressure

coefficients Cp’s from the pressure values measured

by the twelve pressure sensors. The signal was

acquisitioned at sampling rate of 10 kilo samples/s

in frames of 1024 points for each channel which

allowed a boundary layer pressure fluctuations fast

Fourier transform (FFT) spectral decomposition up

to 5 kHz for all channels, at a rate of 9.77 samples/s

using Matlab/Simulink software. The plot results

were visualized in real time on the computer screen

in dedicated windows (see Figure 4) at a rate of 1

sample/sec. Figure 4 shows an example of graphical

user interface in which all the aerodynamic and

morphing shape information were centralized

together with the control buttons of the controlling



ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

118

software. The window shows information about the

Mach number, the angle of attack, the airfoil shape

of the morphing wing, and the two actuators vertical

displacements needed to obtain the desired airfoil

shape. In the two plots, are shown the pressure

coefficients distribution Cp’s of the twelve Kulite

sensors, and the noise of the signal (RMS) of each

pressure signal. Figure 4.a shows the wing un-

morphed position, while the Figure 4.b shows the

wing under its morphed position. The results

obtained are qualitatively very similar to those

obtained in previous studies (Nitcshe, 1989 and

Mangalam, 2004).

Figure 4.a: Un-morphed configuration.

The transition between laminar and turbulent

flow was detected by means of each pressure

signal’s root mean square (RMS). The lower RMS

plot given in Figure 4 shows the normalized quantity

of the pressure signal noise from each Kulite sensor

(star points curve). In the example shown in Figure

4, the RMS plot in the un-morphed configuration

(Figure 4.a) the transition is shown in the fourth

sensor due to the fact that it had the maximum RMS

value.

In Figure 4.a, on the GUI was shown an un-

morphed airfoil by use of a black color. The

actuators reference positions correspond to dY1 = 0

mm and dY2 = 0 mm, the Cp distribution calculated

by XFoil for the reference airfoil (black curve), and

the Cp theoretical values of the sensors shown as

black circles on the Cp distribution curve.

Figure 4.b: Morphed configuration. Graphical User

Interface (GUI) with the control buttons of the software.

In the lower plot of Figure 4.a was shown the N

factor used by XFoil to predict transition for the

reference airfoil (black curve). The critical value N

= 7.34 was used in the simulation to match the

turbulence level T = 0.14% measured in the wind

tunnel using Mack’s correlation (1), and the plotted

values on the figure are normalized (N/N

) (Mack,

1977).

8.43 2.4 log( )

−−⋅

(1)

In the case of an un-morphed configuration, the

predicted transition position was found to be the 6th

position of the sixteen available sensors positions. In

the beginning of wind-tunnel tests, a number of

sixteen sensors were installed, but due to their

removal and re-installation during the next two wind

tunnel tests, four of them were found defective,

therefore a number of twelve sensors remained to be

used during the last third wind tunnel tests so only

twelve Kulite sensors were used for plotting the Cp

distribution and RMS distribution (star plots).

Results predicted for the morphed airfoil were

shown in circles. The morphed airfoil coordinates

were shown as blue curves in the upper part of

MORPHING WING REAL TIME OPTIMIZATION IN WIND TUNNEL TESTS

119

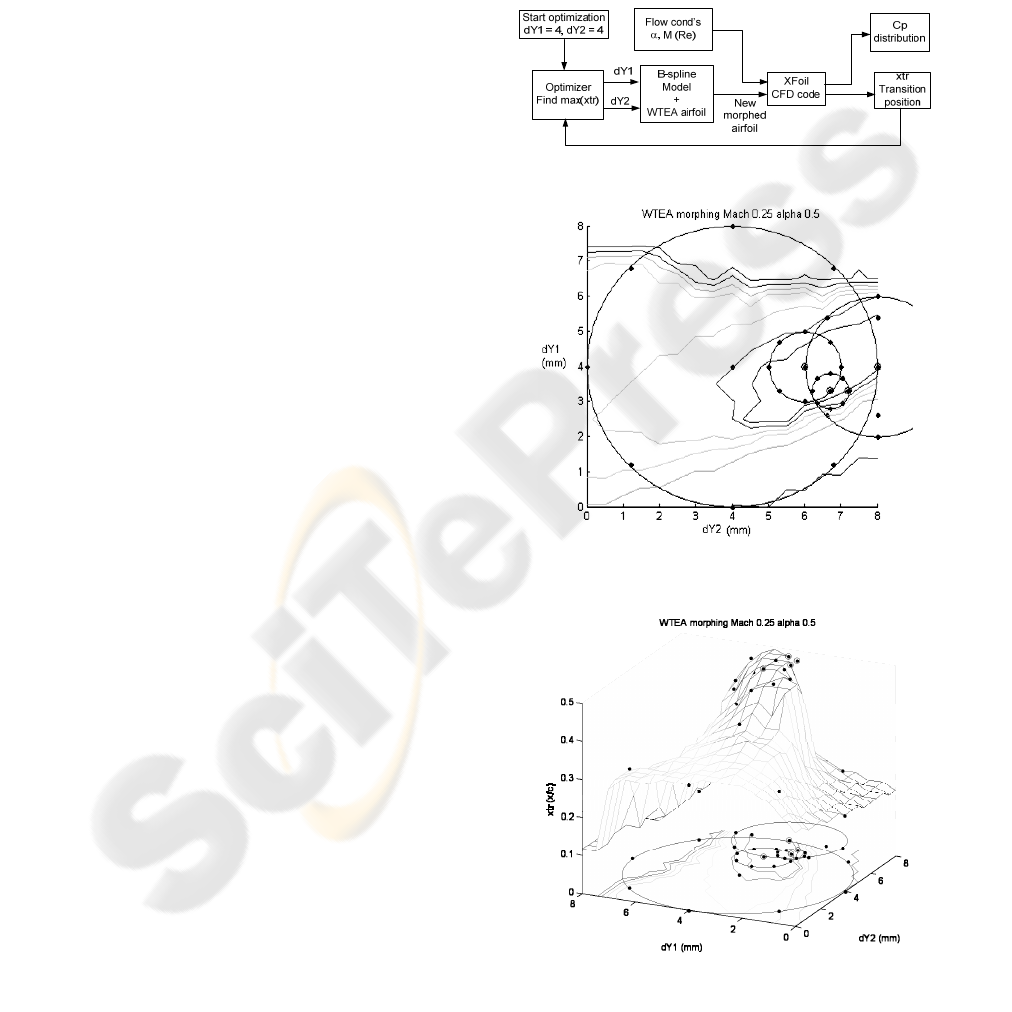
Figure 4.b, the Cp distribution was calculated by

XFoil for the optimized airfoil (circles curve), and

the Cp theoretical values of the sensors were shown

as blue circles on the Cp distribution curve. In the

lower plot of Figure 4.b, the N factor used by XFoil

to predict transition was shown for the optimized

airfoil (circles curve). In this case of morphed

configuration, the predicted position of transition

was the 14th position of the sixteen available sensors

positions.

These lower circles (un-morphed) and upper

circles (morphed) curves served as theoretical

validations of the measured value curves reflecting

the aerodynamic parameters (Cp and RMS) provided

by Kulite sensors in real time with a sampling rate of

1 S/sec. In Figure 4.b is shown the actuated airfoil in

the morphed position (dY1 = 4.92 mm and dY2 =

7.24 mm). The transition position was given by the

sensor location where the maximum RMS was

found, which in this case is the 10th Kulite sensor

out of 12 sensors. The instant visualization allows us

to find the exact position predicted by XFoil.

2.3 Simulation and Experimental

Results Obtained in the Wind

Tunnel

The simulation of the system used as programming

platform the Matlab/Simulink software. The

simulation used the optimization subroutine exactly

the same as in bench tests and wind tunnel tests,

except that in computer simulation and bench test

the aerodynamic pressures that acted upon the skin

and which stimulated the sensors were simulated by

use of XFoil software. As mathematical model of the

flexible skin was used a B-spline with four flexion

points. Two points were fixed where the skin is

glued on the wing rigid structure and two points

were mobile and were placed in the actuators

coordinates on the wing structure. The B-spline

shape that define the airfoil’s flexible skin did not

have the same coordinates as the flexible skin but

was a good approximation for the purpose of

designing an optimization subroutine in closed loop

with a CFD code. Laser scanning during bench tests

showed that the differences between the scanned

airfoils and the theoretical airfoils were less than 0.5

mm (less than 6.25% of the maximum actuators

deflection of 8 mm) (Popov, 2009). The

optimization initialized the algorithm with the values

dY1 = 4 mm and dY2 = 4 mm. Afterwards the

algorithm evaluated the transition point position in

eight points of coordinates (dY1, dY2) situated on a

circle centered in the initial point with a radius of 4

mm within the search domain defined by the bi-

dimensional space of actuators strokes {dY1 = [0,

8], dY2 = [0, 8]}. For each evaluation point, the xtr

value was evaluated by use of XFoil and stored in

the memory. After the first round of evaluations the

optimizer decided which evaluating point had the

maximum value of xtr, which will became the initial

point for the next round of evaluations. The logic

schematic of the optimization subroutine is shown in

Figure 5.

Figure 5: Optimization logic schematic.

Figure 6: Optimization in simulation using XFoil code for

the airflow condition M = 0.25 and

= 0.5º.

Figure 7: Optimization in simulation using XFoil code for

the airflow condition M = 0.25 and

= 0.5º.

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

120

Figures 6, 7 and 10 show the result of WTEA

airfoil optimization after four evaluation rounds, first

evaluation with a radius of 4 mm, second evaluation

with a radius of 2 mm, third evaluation with a radius

of 1 mm and fourth and last evaluation with a radius

of 0.5 mm. As seen in Figure 7 the last round of

evaluation was almost unnecessary because the

maximum x

was found inside a plateau of

maximums with very small differences between

them. Before doing the optimization it was

performed a mapping of the search domain, i.e. for

each combination of dY1 and dY2 in the interval [0

mm, 8 mm] with a step of 1 mm it was found the xtr

and was built the surface x

= f (dY1, dY2) for the

purpose of visualizing the form of the ‘hill’ and to

validate the algorithm in the simulation. Figure 8

and 9 show the same optimization routine that run

during the wind tunnel tests in the same airflow

conditions as the ones simulated except that there

was no map of the searched function. The result was

slightly different because the airfoil shape of the real

flexible skin under wind tunnel conditions was

different than the airfoil shapes defined by use of B-

splines. Still the result was similar, in terms of

actuator strokes dY1 and dY2 as well as the position

of transition. Similarly there could be observed in

Figure 9 a plateau of evaluation points that had the

transition occurrence on the 11th sensor.

Figure 10 shows the result of the airfoil shape

optimization, Cp distribution and xtr transition point

position on the upper surface of the airfoil obtained

through simulation using XFoil and B-splines model

for the flexible skin. The values obtained for wind

flow conditions of Mach = 0.25 and a = 0.5 are dY1

= 3.3 mm and dY2 = 7.2 mm. Also in Figure 7 is

shown the N factor distribution which was the

parameter used by XFoil to calculate the transition

point position. When N factor reached the N

critical

value the transition was triggered. This parameter

was used in wind tunnel to validate the transition

position found through the RMS measuring of the

Kulite pressure sensors.

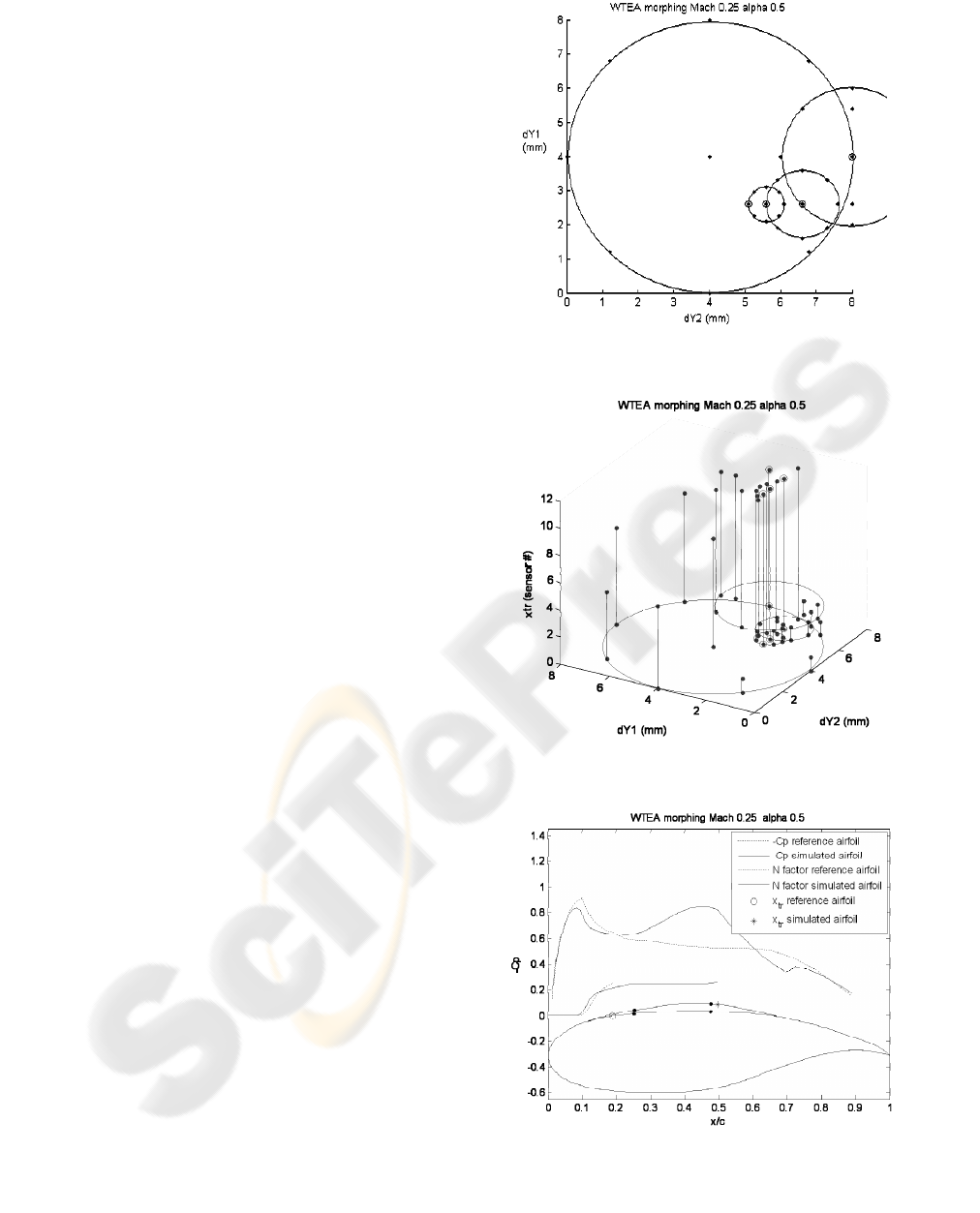
Figure 11 shows the optimized airfoil shape, Cp

distribution and xtr transition point position on the

upper surface of the airfoil in wind tunnel test (star

plots) compared to the optimal airfoil plots (upper

circles) and reference airfoil plots (lower circles)

obtained through simulation. Also in the lower

subplot of Figure 11 the N factor used by XFoil to

detect the transition position was compared to the

RMS of the Kulite sensors. Both the N factor and

RMS were normalized and the purpose of the plots

was to have a visual indicator of the transition

position. The software considered the transition

Figure 8: Optimization in real time during wind tunnel

tests for the airflow condition M = 0.25 and

= 0.5º.

Figure 9: Optimization in real time during wind tunnel

tests for the airflow conditions M = 0.25 and

= 0.5º.

Figure 10: Optimization simulation result for M = 0.25

and

= 0.5°.

MORPHING WING REAL TIME OPTIMIZATION IN WIND TUNNEL TESTS

121

position in the coordinates of the sensor with the

highest noise (RMS) as confirmed by previous

studies (Rioual, 1994). The values obtained in wind

tunnel for wind flow conditions of Mach = 0.25 and

a = 0.5 are xtr /c = 0.635 (xtr =317.5 mm) for the

actuator displacement values dY1 = 2.6 mm and

dY2 = 5.1 mm.

Figure 11: Optimization result during wind tunnel test for

M = 0.25 and

= 0.5°.

Figure 12 shows the time history of the

optimization process in wind tunnel. Due to the long

response of the SMA actuators – the time of cooling

from maximum displacement to zero was approx 2

min – the entire process of optimum search

converged to the optimum values in approx 20 min.

Also, there can be observed that the requested

displacements of the actuators at the maximum

displacement of 8 mm were not realized, due to the

fatigue of the SMA’s accumulated in previous testes.

The maximum deflection was in fact 7 mm for the

first actuator and 6.5 mm for second actuator.

Figure 13 shows typical infrared results obtained

at M = 0.25,

= 0.5° for various configurations.

Only the composite portion of the wing at x/c≤0.7

was shown. The white spots on the wing are the

electronically heated Kulite pressure transducers.

The two lines of SMA actuators, colder than the

model surface, were also visible at quarter chord and

near mid-chord. The locations of the transition in the

images have been highlighted using a white dashed

line: it corresponded to the location of a large

surface temperature gradient, the laminar region

being about 2-3°C hotter than the turbulent region.

The reference airfoil configuration (Figure 13)

Figure 12: Optimization time history during wind tunnel

test for M = 0.25 and

= 0.5°.

Figure 13: Infrared results obtained at M = 0.25 and

0.5° in reference position.

Figure 14: Infrared results obtained at M = 0.25 and

0.5° after optimization.

showed a transition location at x/c = 26%. The

optimization (Figure 14) allowed a laminar

boundary layer run to x/c = 58%, which represented

a significant improvement over the reference case

(Figure 13). Some turbulent wedges caused by

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

122

leading edge contamination, due to dust particles in

the flow, were visible in Figure 10-a. In addition to

providing an on line verification of the Kulite

dynamic pressure signals, the infrared measurement

was particularly useful to detect those early artificial

turbulent regions.

3 CONCLUSIONS

The results of the tests performed in wind tunnel

using a morphing wing were shown. The

optimization method did not use any CFD code but

used the same optimization algorithm in real time.

This optimization converged in approximately 10

minutes due to the slow response of the SMA

actuators especially in the cooling phase of the

cycle. It was observed that the airfoil realized by this

method slightly differs from the optimization using

CFD codes. This result was due to the fact that the

cost function of the optimization (transition position)

had discrete values (the sensors positions) and the

maximum of the function was a plateau of different

dY1 and dY2 values. The optimizer stopped at a

certain value in function of the number and

magnitudes of the searching steps. It was observed

that the last searching step (searching of the

maximum in eight points situated on a circle with

ray of 0.5 mm – see Figure 9) was not necessary due

to the cost function plateau of maximums.

ACKNOWLEDGEMENTS

The authors would like to thank the Consortium of

Research in the Aerospatial Industry in Quebec

(CRIAQ) for funding the present work, and Thales

Avionics and Bombardier Aerospace for their

financial and technical. The authors would like also

to thank George Henri Simon for initiating CRIAQ

7.1 project and Philippe Molaret from Thales

Avionics for their collaboration on this work.

REFERENCES

Allison, D. O., and Dagenhart, J. R., 1978, Design of a

Laminar-Flow-Control Supercritical Airfoil for a

Swept Wing, CTOL Transport Technology, NASA

Langley Research Center, pp. 395–408.

Andersen, G. R. et al., 2007, Aeroelastic modeling,

analysis and testing of a morphing wing structure,

AIAA-2007-1734, pp. 359-373.

Bharti, S. et al., 2006, Optimal structural design of a

morphing aircraft wing using parallel non-dominated

sorting genetic algorithm II (NSGA II), Smart

Structures and Materials 2006: Industrial and Comer-

cial Applications of Smart Structures Technologies,

Proceedings of SPIE Vol. 6166, pp. 1-12.

Coutu, D., Brailovski, V., Terriault, P., 2009, Promising

benefits of an active-extrados morphing laminar wing,

AIAA Journal of Aircraft, Vol. 46(2), pp. 730-731.

De Breuker, R. et al., 2007, Energy-based aeroelastic

analysis of a morphing wing, Proceedings of SPIE,

Vol. 6523, pp. 1-12.

Gandhi, N. et al., 2007, Intelligent control of a morphing

aircraft, Paper AIAA-2007-1716, pp. 166-182.

Georges, T., Brailovski, V., Morellon, E., Coutu, D., and

Terriault, P., 2009, Design of Shape Memory Alloy

Actuators for Morphing Laminar Wing With Flexible

Extrados, Journal of Mechanical Design, Vol. 131,

No. 9, pp. 091006-1–091006-9.

Hackenberg, Petra, 1995, Numerical optimization of the

suction distribution for laminar flow control aerofoils,

Doctoral Thesis, University of Southampton (United

Kingdom).

Hill climbing, From Wikipedia, the free encyclopedia

[online], http://en.wikipedia.org/wiki/Hill_climbing

Jacob, J.D., 1998, On the Fluid Dynamics of Adaptive

Airfoils, Proceedings of ASME International

Mechanical Engineering Congress and Exposition

November 15-20, 1998, Anaheim, CA, USA.

Jacob, J. D., 1999, Aerodynamic Flow Control Using

Shape Adaptive Surfaces, ASME Paper No.

DETC99/VIB-8323, ASME 17th Biennial Conference

on Mechanical Vibration and Noise, Symposium on

Structronics, Mechatronics, and Smart Materials, Las

Vegas, Nevada, September.

Khalid, M., 1993, Navier Stokes Investigation of Blunt

Trailing Edge Airfoils using O-Grids, AIAA Journal of

Aircraft, Vol.30, No.3, pp.797-800

Khalid, M., and Jones, D. J., 1993 , ACFD Investigation of

the Blunt Trailing Edge Airfoils in Transonic Flow,

Proceedings of the Inaugural Conference of the CFD

Society of Canada, Montreal, June14-15.

Love, M. H. et al., 2007, Demonstration of morphing

technology through ground and wind tunnel tests,

Paper AIAA-2007-1729, pp. 337-348.

Mack, L. M., 1977, Transition and Laminar Instability, Jet

Propulsion Laboratory Publication 77-15, Pasadena,CA.

Mangalam, S. M., 2004, Real-Time Extraction of

Hydrodynamic Flow Characteristics Using Surface

Signature, IEEE Journal of Oceanic Engineering, Vol.

29, No. 3, pp. 622-630.

Mébarki, Y., Mamou, M. and Genest, M., 2009, Infrared

Measurements of Transition Location on the CRIAQ

project Morphing Wing Model, NRC LTR- AL-2009-

0075.

Munday, D., Jacob, J. D., and Huang, G., 2002, Active

Flow Control of Separation on a Wing with

Oscillatory Camber, AIAA Paper No. 2002-0413, 40th

AIAA Aerospace Sciences Meeting, Reno, NV.

MORPHING WING REAL TIME OPTIMIZATION IN WIND TUNNEL TESTS

123

Munday, D., Jacob, J. D., T. Hauser, and Huang, G., 2002,

Experimental and Numerical Investigation of

Aerodynamic Flow Control Using Oscillating

Adaptive Surfaces, AIAA Paper No. 2002-2837, 1st

AIAA Flow Control Conference, St. Louis.

Nitcshe, W., Mirow, P., and Dorfler, T., 1989,

Investigations on Flow Instabilities on Airfoils by

Means of Piezofoil Arrays, Laminar-Turbulent

Transition Proceedings of the IUTAM Symposium,

Ecole nationale Superieure de l’Aeronautique et de

l’Espace, Toulouse, France, Sept. 11-15, , Berlin and

New York, Springer-Verlag, 1990.

Popov. A-V., Labib, M., Fays, J., Botez, R.M., 2008,

Closed loop control simulations on a morphing

laminar airfoil using shape memory alloys actuators,

AIAA Journal of Aircraft, Vol. 45(5), pp. 1794-1803.

Popov, A-V., Botez, R. M., and Grigorie, L., 2009,

Morphing Wing Validation during Bench Tests,

Canadian Aeronautics and Space Institute Annual

General Meeting, Aircraft Design & Development

Symposium, 5–7 May, Kanata, Ontario.

Pralits, J., 2003, Optimal Design of Natural and Hybrid

Laminar Flow Control on Wings, Doctoral Thesis,

Technical Report from Royal Institute of Technology,

Stockholm, Sweden.

Rioual, J.-L., Nelson, P. A., and Fisher, M. J., 1994,

Experiments on the Automatic Control of Boundary-

Layer Transition, Journal of Aircraft. Vol. 31, No. 6,

pp. 1416–1418.

Sainmont, C., Paraschivoiu, I., Coutu, D., 2009,

Multidisciplinary Approach for the Optimization of a

Laminar Airfoil Equipped with a Morphing Upper

Surface, NATO AVT-168 Symposium on "Morphing

Vehicles", Evora, Portugal.

Sanders, B. et al., 2003, Aerodynamic and aeroelastic

characteristics of wings with conformal control

surfaces for morphing aircraft, Journal of Aircraft,

Vol. 40(1), pp. 94-99.

Simulated annealing, From Wikipedia, the free

encyclopedia [online], http://en.wikipedia.org/wiki/

Simulated_annealing

Skillen, M. D., Crossley, W. A., 2005, Developing

response surface based wing weight equations for

conceptual morphing aircraft sizing, Paper AIAA-

2005-1960, pp. 2007-2019.

Yang, S.-M. , Han, J.-H., Lee, I., 2006, Characteristics of

smart composite wing withSMA’s and optical fibre

sensors, International Journal of Applied

Electromagnetics and Mechanics, Vol. 23, pp. 177–

186.

Zingg, D. W., Diosady, L., Billing, L., 2006. Adaptive

Airfoils for Drag Reduction at Transonic Speeds,

AIAA paper 2006-3656.

APPENDIX

b = span of wing model (m)

c = chord of wing airfoil (m)

= drag coefficient

= lift coefficient

= pressure coefficient

M = Mach number

N = natural logarithm of rapport between

amplified perturbation and initial

perturbation in laminar flow

Re = Reynolds number

= transition position (m)

= angle of attack of the wing (º)

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

124