
IMPROVING REAL WORLD SCHEMA MATCHING WITH
DECOMPOSITION PROCESS
Sana Sellami, Aïcha-Nabila Benharkat, Youssef Amghar
University of Lyon, CNRS, INSA-Lyon, LIRIS, UMR5205, F-69621, France
Frédéric Flouvat
University of New Caledonia, PPME laboratory BP R4, 98851 Noumea, New Caledonia
Keywords: XML Schemas, Scalable Matching, Decomposition.
Abstract: This paper tends to provide an answer to a difficult problem: Matching large XML schemas. Scalable
Matching acquires a long execution time other than decreasing the quality of matches. In this paper, we
propose an XML schema decomposition approach as a solution for large schema matching problem. The
presented approach identifies the common structures between and within XML schemas, and decomposes
these input schemas. Our method uses tree mining techniques to identify these common structures and to
select the most relevant sub-parts of large schemas for matching. As proved by our experiments in e-
business domain, the proposed approach improves the performance of schema matching and offers a better
quality of matches in comparison to other existing matching tools.
1 INTRODUCTION
Nowadays, within the business area, the industry
builds large scale distributed systems and
middlewares that are more and more based on XML
technology. In fact, there are many databases and
information sources available through the web
covering different domains: semantic Web, deep
Web, E-business, digital libraries, etc. In such
domains, the generated data (XML schemas,
ontologies, etc) are heterogeneous and voluminous.
The presence of vast heterogeneous collections of
data arises one of the greatest challenges in data
integration field. For example, real-life E-business
schemas of catalogs and messages such as BMEcat,
OAGIS
1
or XCBL
2
present an “amazing scale” of
elements (20
≈ 10000 elements). One of the most
critical steps to integrate heterogeneous e-Business
applications that contain different XML schemas is
to use large schema matching.
Matching techniques are solutions to
automatically search correspondences between these
data in order to obtain useful information. In fact,
matching is an operation that takes data as input (e.g
XML schemas, ontologies, relational database
schemas) and returns the semantic similarity values
of their elements. Schema matching has attracted
the attention of research community (Do et al.,
2002) (Rahm et al., 2001). However, most matching
tools are applied on two schemas with human
intervention, whereas in practice, real world
schemas are voluminous. Matching these schemas at
large scale represents a laborious process. Moreover,
matching the whole input schemas will take long
execution time. Then, one of the challenges of the
matching community is to efficiently search for
correspondences between large schemas and to
compute reasonable results in a reasonable time.
Our main motivation is to decrease scalable
match overload. E-business domain has to deal with
large schemas. Matching XML business schemas
have two main characteristics. First, an XML
business schema may include identical redundant
structures called intra-schemas structures or shared
sub-structures. Intra-schemas structures are frequent
within large XML schemas. In fact, there are many
shared XML schema components (elements,
attributes, and types) that are referenced in several
places (figure 1) in a schema.
Second, schemas from the same domains may
share common structures called inter-schemas
structures (i.e. similar structures in different
schemas). These structures represent an important
source of structural and semantic information.
151
Sellami S., Benharkat A., Amghar Y. and Flouvat F. (2010).
IMPROVING REAL WORLD SCHEMA MATCHING WITH DECOMPOSITION PROCESS.
In Proceedings of the 12th International Conference on Enterprise Information Systems - Databases and Information Systems Integration, pages
151-158
DOI: 10.5220/0002887001510158
Copyright
c
SciTePress
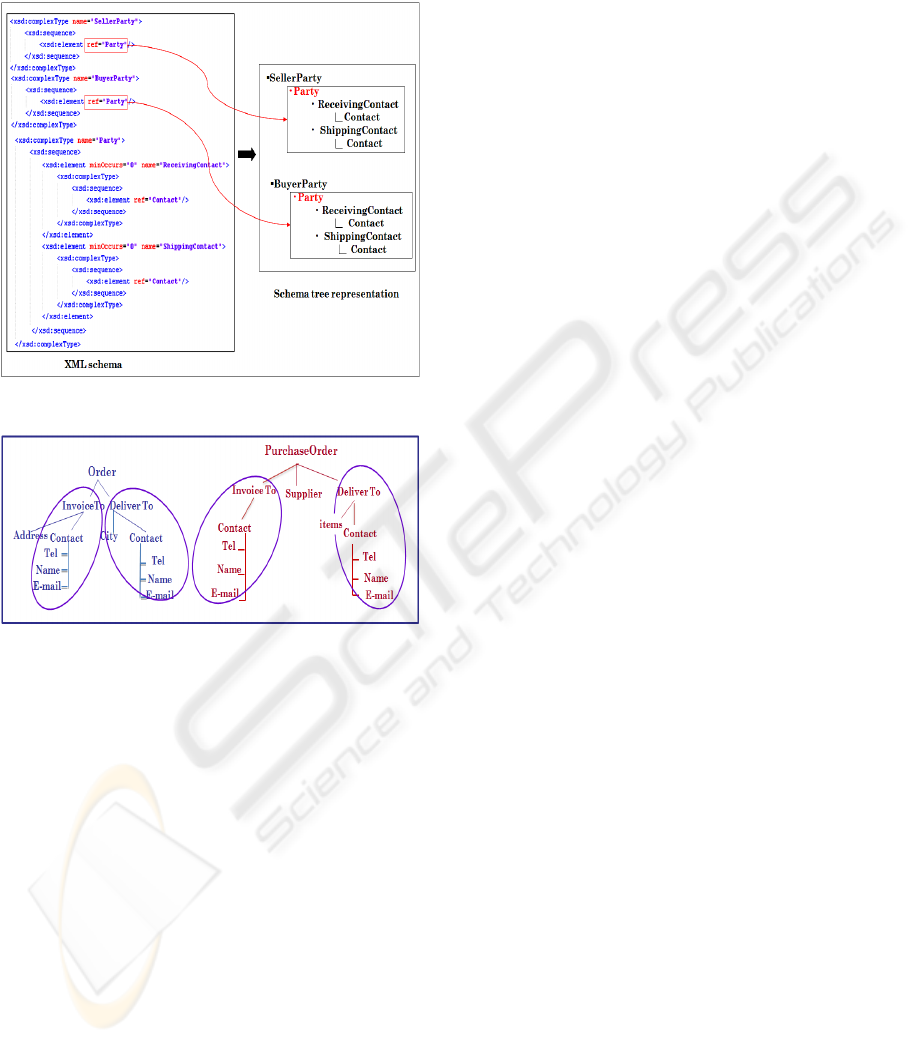
Figure 2 shows an example of the inter-schemas
structures. Both schemas share {Invoice To,
Contact, Tel, Name, E-mail} and {Deliver To,
Contact, Tel, Name, E-mail} sub-schemas.
Figure 1: Schema tree representation.
Figure 2: Example of inter-schemas structures.
Motivated by these observations, we propose an
XML schema decomposition approach based on
inter-schemas and intra-schemas identification. Our
approach attempts to find the most similar parts
between all the schemas, at once. To this end, we
use tree mining techniques to identify these common
structures between and within XML schemas. Tree
mining is a classical data mining problem which has
received lots of efforts in this last years.
Our approach is composed of three steps:
transforming XML schemas into trees, extracting
frequent trees from these transformed schemas and
processing these sub-trees to find the more relevant
candidates for matching.
The goal of our paper is then to provide a pre
matching approach based on decomposing large
schemas into smaller ones to improve the quality
and performance of large schema matching. Then
matching will be performed between small schemas.
The remainder of this paper is organized as
follows. Section 2 reviews the research works
related to the different matching strategies. The aim
of this study is to show how existing works deal
with scalability problem. In section 3, we present
our decomposition approach. Section 4 presents
experimental evaluation results. Finally, we
conclude and discuss future works.
2 RELATED WORK: MATCHING
STRATEGIES
Being a central process for several research topics
like data integration, data transformation, schema
evolution, etc, matching has attracted much attention
by research community. Several matching tools have
been proposed in the literature including different
strategies to deal with scalability problem. These
approaches represent an effective attempt to resolve
large scale matching problem. We distinguish three
different strategies: fragmentation, clustering and
statistical approaches.
• Fragmentation Strategy: This is a divide and
conquers strategy which decomposes a large
matching problem into smaller sub-problems by
matching at the level of fragments. The issue of
fragmentation large-scale schemas and ontologies
has been recently addressed by (Hu et al., 2008),
(Rahm et al., 2004) and (Wang et al., 2006). The
authors (Rahm et al., 2004) presented the fragment-
based approach as an effective solution to
decompose two large schemas into small fragments.
The fragment can be a schema, or sub-schema that
represents parts of a schema which can be separately
instantiated, or shared that is identified by a node
with multiple parents. The proposed strategy is
composed of two matching steps: The first step is
the fragments identification of two schemas and the
second step is to match fragments. This approach
has been implemented in COMA++ tool (Do and
Rahm, 2007). The authors (Hu et al., 2008) propose
a method for partition-based block matching that
considers both linguistic and structural
characteristics of domain entities based on virtual
documents for the relatedness measure. Partitioning
ontologies is achieved by a hierarchical bisection
algorithm to provide block mappings. Like
partitioning approach, Modularization-based
Ontology Matching approach (MOM) (Wang et al.,
2006) decomposes a large matching problem into
smaller sub-problems by matching at the level of
ontology modules. This approach includes sub-steps
for large ontology partitioning, finding similar
modules, module matching and result combination.
This method uses the
ε
-connection to transform the
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
152

input ontology into an
ε
-connection with the largest
possible number of connected knowledge bases.
• Clustering Strategy: This approach has been
proposed by (Pei et al., 2006). First, schemas are
clustered based on their contextual similarity.
Second, attributes of the schemas that are in the
same schema cluster are clustered to find attribute
correspondences between these schemas. Third,
attributes are clustered across different schema
clusters using statistical information gleaned from
the existing attribute clusters to find attribute
correspondences between more schemas.
• Statistical Strategy: This approach has been
introduced by (He et al., 2003) and (He et al., 2004)
with MGS (for hypothesis modeling, generation, and
selection) and a DCM (Dual Correlation Mining)
framework. The MGS framework is an approach for
global evaluation, building upon the hypothesis of
the existence of a hidden schema model that
probabilistically generates the schemas we observed.
This evaluation estimates all possible “models,”
where a model expresses all attributes matchings.
Nevertheless, this approach does not take into
consideration complex mappings. DCM framework
has been proposed for local evaluation, based on the
observation that co-occurrence patterns across
schemas often reveal the complex relationships of
attributes. However, these approaches suffer from
noisy data. HSM (Holistic Schema Matching) and
PSM (Parallel Schema Matching) have been
proposed by (Su et al., 2006) to find matching
attributes across a set of Web database schemas of
the same domain. HSM integrates several steps:
matching score calculation that measures the
probability of two attributes being synonymous,
grouping score calculation that estimates whether
two attributes are grouping attributes. PSM forms
parallel schemas by comparing two schemas and
deleting their common attributes. HSM and PSM are
purely based on the occurrence patterns of attributes
and require neither domain-knowledge, nor user
interaction.
In our work, we propose a decomposition
approach which divides XML schemas into small
sub-schemas with the use of linguistic and tree
mining techniques. Our approach is similar to the
fragmentation strategy. The main difference lies in
the way to find intra-schemas structures called
shared sub-structures in COMA++ (Do and Rahm,
2007). More precisely, our approach extends
fragmentation method to find inter-schemas
structures in automatic manner and is applied on
several schemas at once.
3 XML SCHEMAS
DECOMPOSITION APPROACH
We propose a decomposition approach, as a pre-
matching phase, which break down large XML
schemas into smaller sub-schemas to improve the
performance of large schema matching. Our
approach identifies and extracts common structures
between and within XML schemas (inter and intra-
schemas) and finds the sub-schemas candidates for
matching.
As illustrated in figure 3, our proposed approach
is composed of three phases: (1) converting XML
schemas in trees, (2) identifying and mining frequent
sub-trees, (3) finding relevant frequent sub-trees.
Our approach is based on the following
observations and assumptions: a) Schemas at large
scale are various and voluminous, b) Schemas in the
same domain contain the same domain concepts, and
c) In one schema, several sub-schemas are
redundant.
We discuss in this section the different phases of
decomposition approach.
Figure 3: Decomposition approach.
3.1 XML Trees:
From Schemas to Trees
The goal of this initial phase is to transform XML
schemas into trees and to find linguistic relations
between elements. This aims at improving
decomposition with considering not only exactly the
same labels of elements but also the linguistic
similar elements.
We firstly need to parse the XML schemas and
transforming them into trees. The main feature of
these large schemas is that they contain referential
constraints. Then parsing these schemas becomes a
difficult exercise. To cope with these constraints, we
duplicate the segment which they refer to resolve
their multiple contexts. We notice that most previous
match systems focused on simple schemas without
referential elements.
An XML schema is then modeled as a labeled
unordered rooted tree. Each element or attribute of
IMPROVING REAL WORLD SCHEMA MATCHING WITH DECOMPOSITION PROCESS
153
the schema is translated into a node. The child
elements and attributes are translated into children of
the element node. The names, types and constraints
of elements and attributes represent the labels of the
nodes.
We present the formal definition of basic XML
tree concept.
Definition 1 (XML Tree). T= (r, N, E,
ϕ
) is a
labeled unordered rooted tree, where r is the root, N
is a set of nodes (elements or attributes), E is the set
of edges, and
ϕ
is a labeling application
ϕ
: N →
L assigning a label (element name, type or
constraint) to each node of the tree, where L is the
set of labels of nodes.
Definition 2 (Tree Size and Depth). T= (r, N, E,
ϕ
) is a labeled unordered rooted tree. The size of T,
denoted |T| is the number of nodes in T. The depth
of a node N is the number of ancestors of N. The
root node is at depth zero.
Moreover, we parse the element names and
gather them into sequences of tokens. A tokenizer
identifies punctuation (e.g PARTY_IDÆ <Party,
ID>), special symbols, etc. We use WorldNet
thesaurus to find synonym elements. This analysis
allows the identification of the most relevant
elements in the next step. These elements are then
mapped into integer representation to make faster
the mining process.
3.2 Identifying and Mining Frequent
Sub-trees
The main goal of this phase is to decompose the
input schemas into smaller ones. To this end, we
identify and extract the common sub-structures from
XML schemas describing the same domains. Then
we distinguish between two sub-structures: inter
and intra schemas structures.
Inter-schemas: They are the common structures
between different XML schemas. They represent an
important source of structural and semantic
information
Intra-schemas: They are the frequent structures
within an XML schema. Identifying such structures
plays a key role for decomposition.
The problem of discovering these structures can be
defined as follows:
Frequent Tree Mining. Given a set of trees F (also
called the forest) and a user defined threshold
σ
, the
problem is to find all the sub-trees included at least
σ
times in F. The solutions are called the frequent
trees of F w.r.t.
σ
.
Definition 3 (Tree Inclusion). Let T
1 = (r1, N1, E1,
ϕ
1) be a labeled unordered sub-tree and T2 = (r2, N2,
E
2,
ϕ
2) be a labeled unordered tree. T1 is included
into T
2 (noted T1 ⊆ T2) if there exists an injective
mapping M: N
1 → N2 that satisfies the following
rules:
R
1 : M preserves the labels :
∀
u
∈
N1 ,
ϕ
1
(u)=
ϕ
2 (M (u)) (
ϕ
: N → L is an application that
assigns a label to each node).
R
2 : M preserves the parent (a) and ancestor
relationship (b) :
(a)
∀
u, v
∈
N1 , (u, v) ∈ E 1 ⇔ (
M
(u),
M
(v))
∈
E 2
(b)
∀
u, v
∈
N
1
si (u, v)
∈
E
1
⇔ (
M
(u),
M
(v))
∈
E
2
+
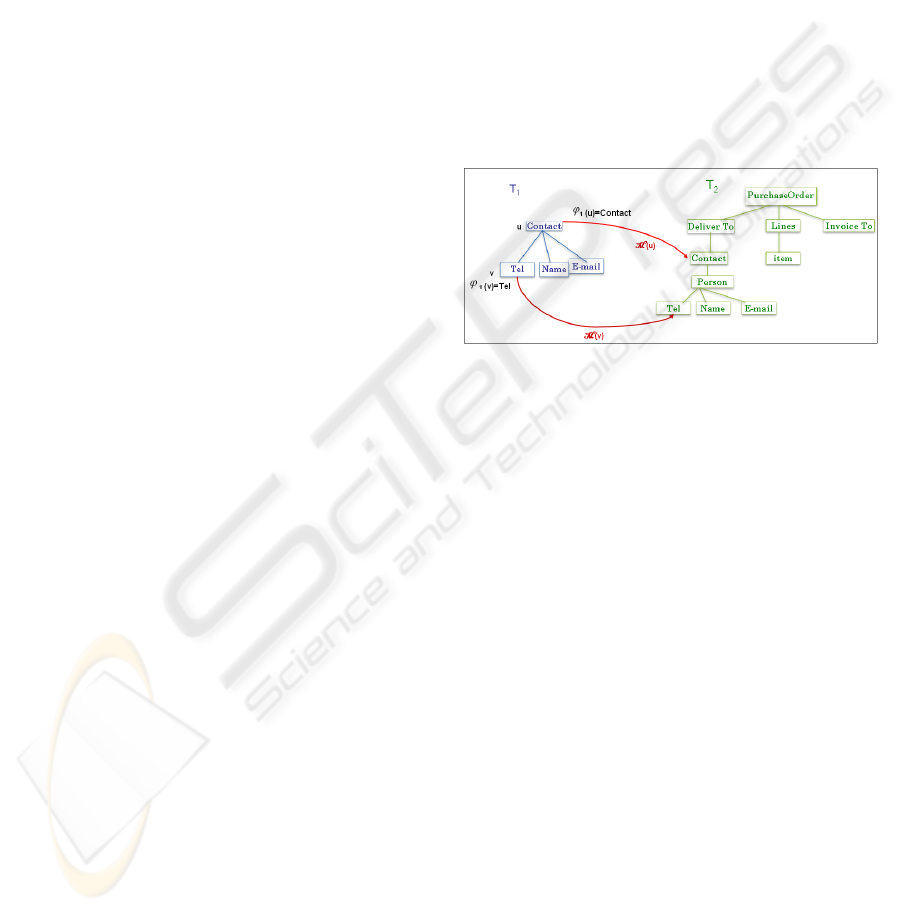
Figure 4: Example of tree inclusion.
We consider the tree inclusion as shown in
Figure 4 T1 = (r1, N1, E1,
ϕ
1) and T2 = (r2, N2, E2,
ϕ
2
) are two trees.
T1 ⊆ T2 means That:
R
1:
∃
u
∈
N1 |
ϕ
1 (u)= Contact ⇒
ϕ
1 (u)=
ϕ
2
(
M
(u))= Contact
R
2:
∃
u, v
∈
N1 | (u, v)
∈
E 1 ⇔ (
M
(u),
M
(v))
∈
E2
+
The frequency is computed using the notion of
frequency support. The support of a tree X is noted
Support(X,F). The basic definitions of these
concepts are listed as follows:
Definition 4 (Frequency Support). Let F = {T
1
,
T
2
,… T
n
} be a set of trees (or forest).
The frequency Support of a tree X noted
Support(X,F) is defined as:
Support(X,F) =
∑
=
n
i 1
intra-support( X,Ti)
Where intra-support( X, T
i) is the number of
occurrence of X in T
i Note that this support
definition considers both intra and inter-schemas.
Definition 5 (Frequent Tree). A tree X is said to be
frequent in a forest F w.r.t. a minimum support
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
154

threshold
σ
iff Support(X,F) ≥
σ
.
The set of all frequent trees of a forest is noted FT =
{FT
1
, FT
2
, …, FT
i
} and FT
i
= {FT
i1
, FT
i2
, …, FT
in}
represents the set of elements in the frequent tree FT
i
Figure 5: Example of frequent tree mining.
Figure 5 illustrates an example of frequent tree
mining. For a threshold
σ
=2, the sub-tree X
containing the nodes {Contact, Tel, Name and E-
mail} appears in T
1
, T
2
and T
3
. The intra-support of
X in T
1
, T
2
and T
3
is respectively 2, 1 and 2.
Consequently, Support (X, F) = 5
σ
and X is a
frequent tree FT.
We propose to use tree mining techniques to
identify these common structures. More precisely,
we use the algorithm proposed by (Termier et al.,
2004). Tree mining is a classical pattern mining
problem (an important class of data mining problem)
which aims at discovering automatically sub-trees
that appear frequently in a set of trees.
3.3 Relevant Frequent Sub-trees
Calculus
The focus of this phase is to identify the sub-trees
candidates for matching. This aims at reducing
match effort by only matching relevant parts from
the other schemas. These sub-schemas are then
selected for matching.
This pre-matching phase includes two main steps:
3.3.1 Selection of Maximal Sub-trees
The goal of this operation is to find the maximal
frequent trees to avoid redundant calculation
between the same nodes. Our approach pruned out
all the minimal ones (FT
min
) (see Def. 6).
Definition 6 (Minimal Frequent Sub-tree). A
frequent sub-tree is said to be minimal (FT
min
)
⇔¬∃ FT ⊆ FT
min
/ FT is a frequent sub-tree
3.3.2 Finding Similar Sub-trees
The goal of this step is to identify the most similar
sub-trees (FT
Sim
) for matching. This is done in two
phases:
a) Testing the Linguistic Similarity between
Element Sub-trees to Find the Most Related Nodes
The objective is to find similar nodes between the
frequent sub-trees. This similarity (Sim
edit
) is done
with the use of edit distance function (Cohen et al.,
2003).
Sim
edit (FTsi, FTTj) = 1- (edit_distance (FTsi, FTTj) /
max (length (FT
si), length (FTTj)))
b) Computing the Similarity Measure between
Frequent Trees:
Definition 7 (Frequent Tree Similarity). Let FT
S
and FT
T
two frequent trees source and target
N
c
represents the set of all the common and
similar element pairs between FT
S
and FT
T
: N
c
=
{(FT
si
, FT
Tj
) | Sim
edit
(FT
si
, FT
Tj
)
≥
0.4 }
The similarity (Sim
s
) between FT
s
and FT
T
is:
Sim
s
(FT
S
, FT
T
)= | N
c
| / | FT
s
∪
FT
T
|
where Sim
s
(FT
S
, FT
T
) value is included in [0,1].
| N
c
|: represents the cardinality of N
c
3.3.3 Pre-matching Algorithm
Figure 6: Pseudo-code of pre-matching phase.
IMPROVING REAL WORLD SCHEMA MATCHING WITH DECOMPOSITION PROCESS
155

3.4 Matching Sub-schemas
In this phase, the resulted sub-schemas of
decomposition approach are selected for matching.
Then matching large schemas is reduced to the
matching of much smaller ones. For every pair of
schemas of FT
cand
set, we apply our matching
algorithm called EXSMAL (Chukmol et al., 2005) to
discover semantic and structural correspondences
between pair of schema elements (figure 7). Our
algorithm considers the element types, descriptions
(basic similarity) and structural similarities.
Structural similarity is very important because, the
same element may appear in many different
contexts, for example, DeliverTo.Address and
BillTo.Address which should be differentiated for a
correct matching.
Algorithm EXSMAL
Input: FT
S
, FT
T
: two XML sub-schemas source and
target
Ouput: set of triplets < FT
si
, FT
Tj
, V
sim
>
With FT
si
, an element of FT
s
,
FT
Tj
, an element of FT
Tj
V
sim
the similarity value between FTsi and FTTj
Figure 7: Short description of EXSMAL algorithm.
4 EVALUATION
We conducted our experiments on real XML
schemas (XCBL
1
and OAGIS²). XCBL (XML
Common Business Library) is a set of XML
schemas for business-to-business e-commerce. The
standard OAGIS (Open Application Group Inc.)
represents a set of business process schemas. The
main goal of our experiments is to show that our
approach deals with both quality and performance of
large schema matching. We have implemented the
XML schema parser, the decomposition approach in
our PLASMA (Platform for LArge Schema
MAtching) prototype. Firstly, we evaluate the
performance of schema parsing comparing to
COMA++ tool and schema matching execution.
Secondly, we determine the quality of matching that
we use to compare with fragmentation results of
COMA++ tool.
Experimental Environment. Our experiments were
conducted on a Windows machine with a 2.80GHz
Intel Pentium and 2Go RAM.
Table 1 summarizes the major characteristics E-
business schemas
Table 1: Characteristics of E-business schemas.
1
www.xcbl.org,
2
www.oagi.org
4.1 Parsing XML Schemas Evaluation
We have evaluated the time elapsed in loading and
parsing XML schemas by our parser implemented
within PLASMA and compared in the same
conditions with the time elapsed by COMA++. This
experience was done on medium schemas with 245
elements (154ko), large schemas with 630 elements
(330ko) and very large with 3796 elements (950ko).
Parsing schemas depends on elements number and
on files size. Figure 8 illustrates these results
showing clearly a better performance of the
PLASMA parser. In fact, COMA++ loads schemas
in a repository before parsing. This step is very low
and can spent several minutes for very large
schemas.
0,085
29
0,9
38
8
156
0
20
40
60
80
100
120
140
160
se conds
Medium Large Very Large
sch em a s siz e
Evaluation of Loading and Parsing XML schemas
PLASMA
COMA++
Figure 8: Parsing XML schemas by PLASMA and
COMA++.
4.2 Performance of Decomposition
Approach
We have evaluated the performance of the
decomposition approach applied on different size of
schemas (medium, large and very large) and
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
156
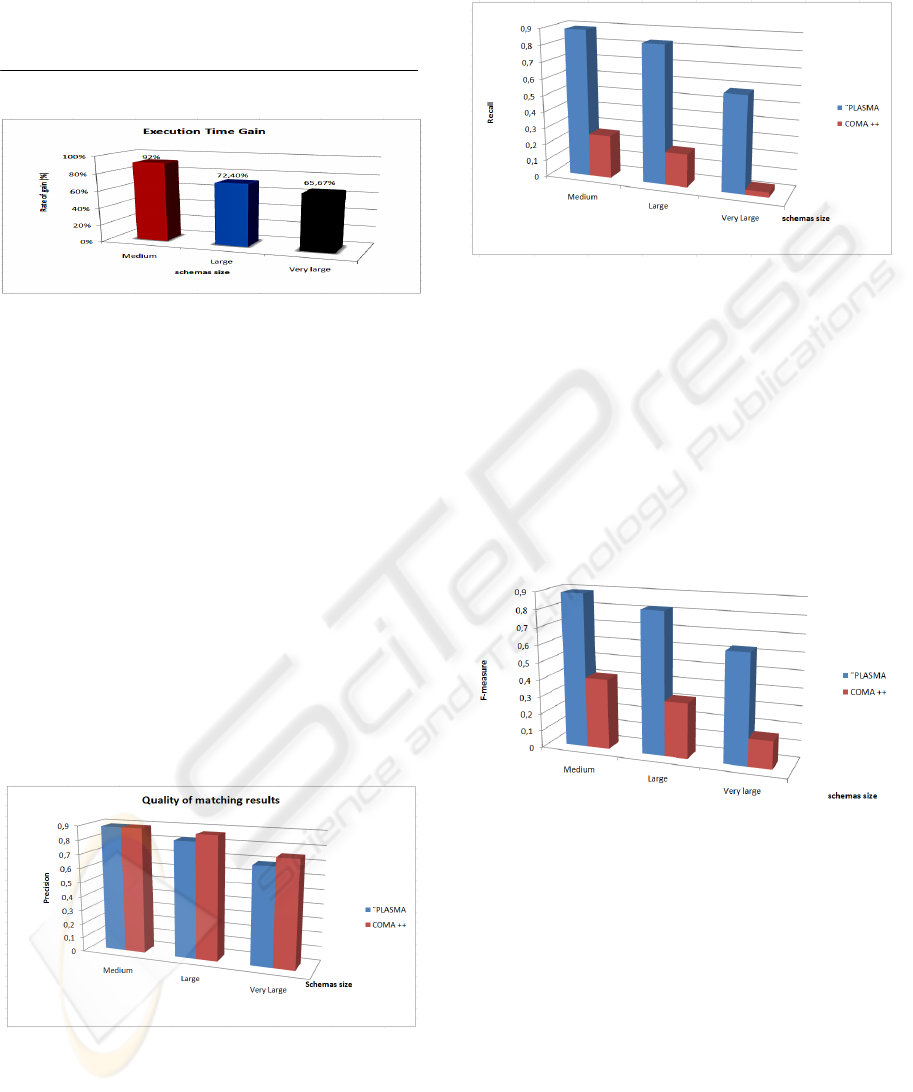
compare it with the approach without decomposition
(direct matching with EXSMAL). The performance
is described in terms of the execution time gain
(figure 9) defined as follows:
Execution_time_gain =
iondecompositwithoutexecutiontime
iondecompositexecutiontimeiondecompositwithoutexecutiontime
___
_____ −
Figure 9: Execution time gain with decomposition
approach.
We have observed that using our decomposition
approach, we optimize the EXSMAL matcher’s
execution (e.g 65.67% for the very large schemas).
Note that, in our experimentations, the execution
time of the tree mining algorithm is only few
seconds.
4.3 Quality of Matching
To determine the quality of a decomposition
approach, we use the three metrics namely precision,
recall and f-measure (Do et al., 2002). We
compared our decomposition results with those of
fragmentation COMA++ approach. PLASMA and
COMA ++ have been tested within the same
experimental conditions. Furthermore, COMA ++ is
configured to be as close as possible to PLASMA.
Figure 10: Precision obtained by decomposition approach
in PLASMA and fragmentation approach in COMA++.
Figure 10 shows the precision for the PLASMA
decomposition and COMA++ fragmentation
approaches. In the medium schemas, PLASMA and
COMA++ achieve a higher precision value.
However, precision decreases with growing schema
size.
Figure 11: Recall obtained by decomposition approach in
PLASMA and fragmentation approach in COMA++.
Figure 11 depicts the recall of the both matching
strategies in PLASMA and COMA++. The results
proved that our decomposition approach
outperforms the fragmentation approach. This is due
to limitation of the fragmentation approach to find
only the shared fragments (or intra-schemas). Unlike
our approach, fragmentation does not cover all the
possible matches. F-measure is given in figure 12.
Due to its previous recall results, COMA++ obtains
a lowest f-measure than PLASMA.
Figure 12: F-measure obtained by decomposition approach
in PLASMA and fragmentation approach in COMA++.
5 CONCLUSIONS
In this paper we have proposed a decomposition
approach as a first attempt to reduce large scale
matching problem. Our approach identifies common
structures between and within XML schemas and
tries to break down these input schemas. Our aim is
to find the most similar sub-schemas between large
input schemas using scalable and efficient
techniques. Then we have described the way to
effectively decompose large XML schemas using
tree mining and our proposed pre-matching
algorithms. The originality of our work w.r.t.
IMPROVING REAL WORLD SCHEMA MATCHING WITH DECOMPOSITION PROCESS
157

existing approaches is the techniques used to
decompose several schemas at once in a scalable and
automatic manner. Our experiments confirm that the
most of schemas from the same sub-domains share
an important rate of common structures and
matching is more efficient. Moreover, experiments
show that decomposition approach provides a better
quality of matching in comparison to the
fragmentation approach in COMA++.
In the future, we plan to do further experiments
with more XML schemas and complete our
PLASMA system implementation with Wordnet and
edit distance function.
REFERENCES
Chukmol, U., Rifaieh, R. and Benharkat, A.,2005.
EXSMAL: EDI/XML semi-automatic Schema
Matching Algorithm. In the 7
th
International IEEE
Conference on E-Commerce Technology (CEC), pp.
422—425.
Cohen William W., Ravikumar P., Fienberg S.E., 2003. A
Comparison of String Distance Metrics for Name-
Matching Tasks. In Proceedings of IJCAI-03
Workshop on Information Integration on the Web, pp.
73—78.
Do, H.H., Melnik, S., and Rahm, E., 2002. Comparison of
schema Matching Evaluations. In GI-Workshop Web
and Databases. Erfurt, Germany, pp.221—23.
Do, H.H., and Rahm, E., 2007. Matching large schemas:
Approaches and evaluation. In Journal of Information
Systems, pp 857-885.
He, B., Chen-Chan Chang, K.n 2003. Statistical Schema
Matching across Web Query Interfaces. In
Proceedings of the ACM SIGMOD International
Conference on Management of Data, pp. 217—228.
He, B., Chen-Chan Chang, K.,Han, J.,2004. Discovering
complex matchings across Web Query Interfaces: A
Correlation Mining Approach. In Proceedings of the
Tenth ACM SIGKDD International Conference on
Knowledge Discovery and Data Mining (KDD), pp.
148--157, ACM Press New York, NY.
Hu W., Qu Y., Cheng G.,2008. Matching large
ontologies: A divide-and-conquer approach. Journal
on Data and Knowledge Engineering, 67, 140—160
Pei, J., Hong, J., Bell, D.A.,2006. A Novel Clustering-
based Approach to Schema Matching. In Proceedings
of the 4th International Conference on Advances in
Information Systems (ADVIS), pp. 60--69
Rahm, E., Bernstein, P.A., 2001.A survey of approaches to
automatic schema matching. In The International
Journal on Very Large Data Bases.
Rahm E., Do H.H. , and Maβmann S., 2004. Matching
Large XML Schemas. In SIGMOD Record. ACM
Press, NY, vol.33, pp. 26--31, New York
Su, W., Wang, J., Lochovsky, F., 2006. Holistic Schema
Matching for Web Query Interface. In Proceedings of
the 10
th
International Conference on Extending
Database Technology (EDBT), pp. 77—94
Termier A., Rousset M-A., Sebag M.,2004. DRYADE: a
new approach for discovering closed frequent trees in
heterogeneous tree databases. In Proceedings of the 4
th
IEEE International Conference on Data Mining
(ICDM), pp. 543—546
Wang Z., Wang Y., Zhang S., Shen G., Du T., 2006.
Matching Large Scale Ontology Effectively.
Proceedings of the First Asian Semantic Web
Conference (ASWC), pp. 99—106.
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
158
