ITERATIVE IMAGE RECONSTRUCTION METHODS IN CONE

BEAM CT APPLIED TO PHANTOM AND CLINICAL DATA

W. Qiu, M. Soleimani, C. N. Mitchell

Dept. of Electronic and Electrical Engineering, University of Bath, Bath, BA2 7AY, U.K.

T. Marchant, C. J. Moore

The Christie NHS Foundation Trust, Wilmslow Road, Manchester, M20 4BX, U.K.

Keywords:

Iterative reconstruction algorithms, Cone beam CT.

Abstract:

Cone beam computed tomography (CBCT) enables a volumetric image reconstruction from 2D projection

data. In CBCT reconstruction, iterative methods of image reconstruction offer the potential to generate high

quality images and would be an advantage especially for sparse data sets. CBCT image reconstruction software

has been developed based on Multi-Instrument Data Analysis System (MIDAS) tomography toolbox. In this

paper, we present a comparative study of SIRT and ART algorithms, developed in MIDAS platform. The

results will be shown using phantom and clinical patient data.

1 INTRODUCTION

Cone beam computed tomography (CBCT) provides

a volumetric image reconstruction from tomographic

projection data, while in commercial CT system,

though many algorithms exist, ﬁltered back projec-

tion (FBP) like reconstruction algorithm based on

FDK (Feldkamp et al., 1984) is still being used.

Recently, iterative reconstruction algorithms are be-

ing investigated for clinical application (Wang et al.,

2009), as challenges still exist for image reconstruc-

tion due to computational time, parameters selec-

tion and down sampled data in some practical ap-

plications. Iterative algorithms provides an alterna-

tive for commercial tomographic image reconstruc-

tion methods. In this paper the iterative methods have

been studied and results show that they have potential

to performed better in various situations, especially

when projection data are not fully available (Ander-

sen, 1989). In addition, most of the papers describe

the behaviour of iterative algorithms by using phan-

tom data only (Mueller et al., 1999) without applying

to clinical patient measurement. In our work, compar-

ison of the CBCT iterative algorithms (ART (Gordon

et al., 1970) and SIRT (Gilbert, 1972)) implemented

in the Multi-Instrument Data Analysis System (MI-

DAS) (Mitchell and Spencer, 2003) tomography soft-

ware are presented by applying to phantom and clin-

ical data. Convergence rate, edge recovery, compu-

tational time and quality of the image are the main

criteria for considerations. Results are presented with

the image reconstructed from full data sets of CBCT

projection data using iterative algorithms (ART and

SIRT). They are compared in terms of the criteria

mentioned while a FDK image from the same system

is used as a reference.

2 THE CBCT SYSTEM AND DATA

In this study, the measured projection data were

provided by North Western Medical Physics at The

Christie hospital in Manchester. A ’RANDO’ anthro-

pomorphic head phantom

was scanned to produce

360 X-ray projection images, approximately evenly

spaced over an angular range of -100 to +100 de-

grees. Images were acquired at 100kV, 10mA and

10ms per projection, with total imaging dose of ap-

proximately 1.5mGy. Each projection image contains

512x512 pixels of dimension 0.8x0.8mm. Figure 1

shows the imaging system used in this study.

Using the full 360 projection data set a 3D re-

construction of 256x256x256 voxels with resolution

1mm in each direction was produced using iterative

The Phantom Laboratory, Salem, NY, USA.

550

Qiu W., Soleimani M., N. Mitchell C., Marchant T. and Moore C. (2010).

ITERATIVE IMAGE RECONSTRUCTION METHODS IN CONE BEAM CT APPLIED TO PHANTOM AND CLINICAL DATA.

In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 550-553

DOI: 10.5220/0002892005500553

 SciTePress

Figure 1: Medical linear accelerator with integrated X-ray

cone-beam CT system.

techniques. A ’reference image’ was reconstructed

using the COBRA cone beam software developers

package from EXXIM

. This contains an implemen-

tation of FDK FBP, which is a useful benchmark for

the iterative techniques described in this paper.

3 METHODS

The classic ART algorithm is

(i+1)

= f

(i)

+ λ

−

∑

n=1

(i)

∑

n=1

(1)

where λ is the relaxation parameter, which controls

the convergence rate. f (x,y, z) are the image values;

j is the index for the voxel of f ; i is the number of it-

eration; p is the projection data; k is the total number

of rays. N is the number of cells; w is the weight-

ing factor and k is the kth image cell intercepted by

the nth ray. Including a relaxation parameter can im-

prove the quality of ART reconstructions, but usually

at the expense of the speed of convergence. Depend-

ing on the application, different strategies are applied

for choosing the most appropriate relaxation parame-

ter and other settings. Besides ART, there is another

approach of implementation, which is SIRT and de-

ﬁned as

(i+1)

= f

(i)

+ λ

∑

n=1

−

∑

n=1

∑

n=1

]

∑

n=1

(2)

The convergence of the algorithms are used by

comparing the mearused and calculated projection

data, we deﬁne residual norm as

||x|| =

+ x

+ ... + x

, {1 ≤ k ≤ N },

where x is a vector of the difference between the

calculated and measured data. The differences be-

tween the iteratively calculated and measured projec-

tion data are then used for comparison as deﬁned in

Equation 3.

Exxim Computing Corporation, Pleasanton, CA, USA.

E = ||p

(i)

− p|| (3)

In the mean while, a good residual norm result

may not always indicate a good reconstructed image,

as it considers the reconstruction from the projection

data side and one may not expect the projection data

differences to be minimised for the best image, since

the forward projection does not take into account all

physical processes affecting formation of the projec-

tion data. Therefore, comparison is made between

images. Besides norm differences comparison, im-

age row proﬁles are used, concentrating the edge area

in Equation 4.

P =

∑

a=1

f (a, b,c), {b ∈ Z,c ∈ Z | 1 ≤ b ≤ N,1 ≤ c ≤ N }

(4)

To compare with the reference image, a scaling

parameter σ have been used

∆P = σP

re f

(5)

4 RESULTS

The new iterative software has been tested using sim-

ulated data as well as phantom data. This has also

been use for clinical data. Some results are presented

here. Figure 2 shows reconstruction of phantom data

using ART, SIRT and FDK.

Due to the different behaviour of ART and SIRT,

different range of λ are applied. Figure 3 presents the

convergence of ART and SIRT, where ART is with

λ of 0.0146 while SIRT with λ of 0.45 respectively.

It is clearly shown that ART owns a much quicker

convergence than SIRT and according to our imple-

mentation, it takes about three times more for SIRT to

converge the same level of mismatch projection errors

as ART.

The computational time for each ART and SIRT

iteration is shown in Table 1. It contains not only

for full data set, but also down sampled data. The

computer used is 64 bit 3.33GHz Linux with ram of

32GB.

Table 1: Time cost for one ART and SIRT iteration with

available data.

Full data 1/2 data 1/3 data 1/5 data

ART 1600s 800s 540s 320s

SIRT 2200s 1100s 740s 440s

Image row proﬁles of different iterative algo-

rithms comparing to FDK are then implemented as

ITERATIVE IMAGE RECONSTRUCTION METHODS IN CONE BEAM CT APPLIED TO PHANTOM AND

CLINICAL DATA

551

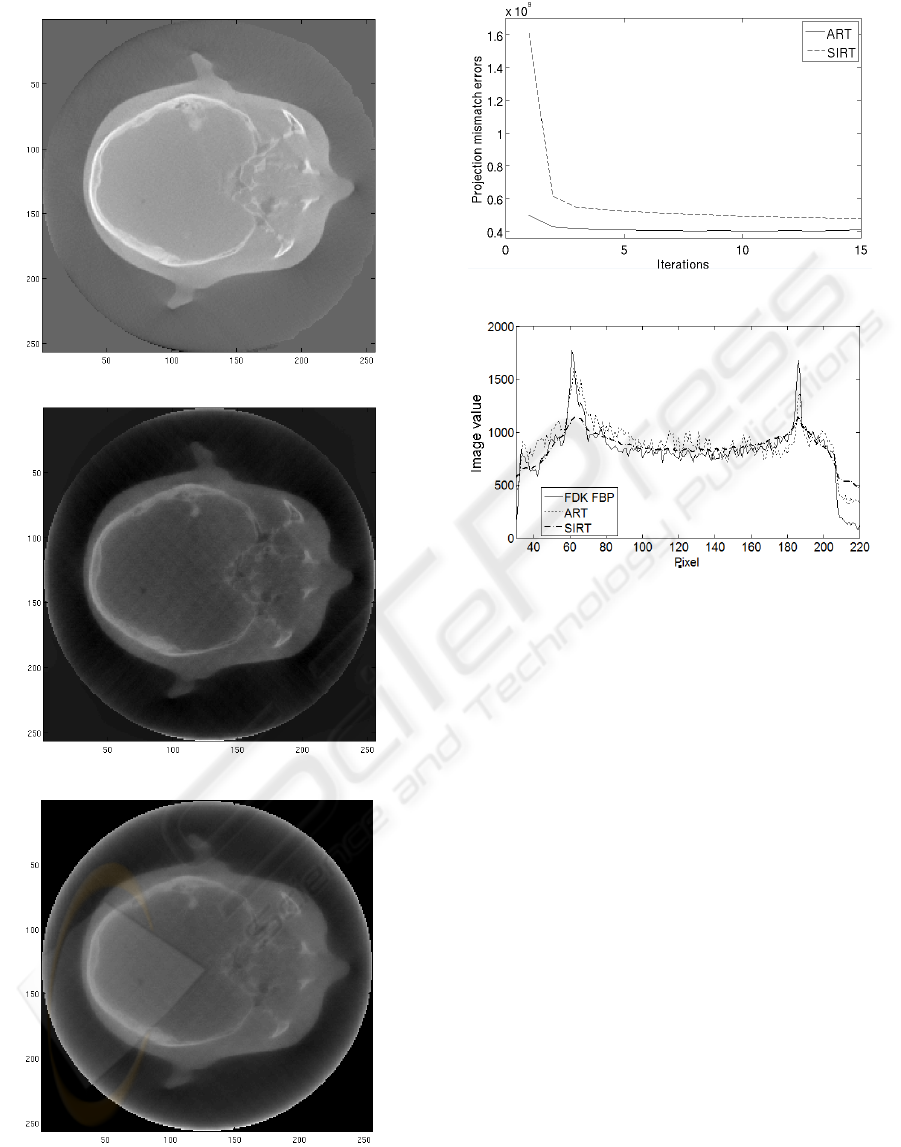
(a) FDK reconstruction

(b) ART reconstruction

Figure 2: Reconstruction with different algorithms using

phantom data.

Figure 3: Convergence for ART and SIRT.

Figure 4: Image proﬁles for ART, SIRT and FDK FBP at

f (x = 128, y,z = 128).

shown in Figure 4, where ART is with λ of 0.0146 at

the 8th iteration using full data set while SIRT with λ

of 0.45 at the 40th iteration using full data set respec-

tively. Because ART is sequential method, in which

only a single projection is used in each step, whereas

SIRT uses all projections in each step simultaneously.

SIRT owns a better uniformity than ART and Figure

4 illustrates the expectation. Both the proﬁles of ART

and SIRT are closely ﬁt with the plot of the proﬁles of

FDK. However, compared to SIRT, the plot of ART

is more ﬂuctuated, especially from y = 60 : 180. The

visualised images of ART (with λ of 0.0146, 8th iter-

ation, full data) and SIRT (with λ of 0.45, 40th itera-

tion, full data) are presented in Figure 2(b) and 2(c).

The implementation and phantom results suggest

that the ART is more efﬁcient provides suitable re-

sults, but by considering the quality of the recon-

structed image, SIRT performs better due to the fact

that ART is sequential method but SIRT updates the

image simultaneously. Figure 5 shows reconstruction

of ART and SIRT compared to commercial FDK in

clinical patient data.

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

552

(a) FDK reconstruction

(b) ART applied to clinical data

Figure 5: Reconstruction with different algorithms using

clinical patient data.

5 CONCLUSIONS

Iterative reconstructions using ART and SIRT are in-

vestigated and implemented in MIDAS. Convergence,

computational time, edge recovery and reconstructed

images are considered. The results indicate that ART

converge faster than the SIRT while SIRT has a better

uniformity. The reconstructed image of ART can be

improved by updating simultaneously which is con-

sidered as simultaneous algebraic reconstruction tech-

nique (SART) (Andersen and Kak, 1984) while in

terms of speed, various methods exist such as GPU

computing which can potential improve the speed by

a factor of 40-100 times.

In our continued effort we are working towards

further optimisation of iterative methods as well as

their clinical relevance, especially when down sam-

pled data are applied. The MIDAS platform will en-

able us to develop further innovative approaches. As

this work is rapidly progressing and we are hoping to

present more results during conference presentation.

REFERENCES

Andersen, A. H. (1989). Algebraic reconstruction in CT

from limited views. IEEE Transactions on Medical

Imaging, 8(1):50–55.

Andersen, A. H. and Kak, A. C. (1984). Simultaneous alge-

braic reconstruction technique (SART): a superior im-

plementation of the ART algorithm. Ultrasonic imag-

ing, 6(1):81–94.

Feldkamp, L. A., Davis, L. C., and Kress, J. W. (1984).

Practical cone-beam algorithm. Journal of the Optical

Society of America A, 1(6):612–619.

Gilbert, P. (1972). Iterative methods for the three-

dimensional reconstruction of an object from projec-

tions. Journal of Theoretical Biology, 36(1):105–117.

Gordon, R., Bender, R., and Herman, G. T. (1970). Al-

gebraic reconstruction techniques (ART) for three-

dimensional electron microscopy and X-ray photogra-

phy. Journal of Theoretical Biology, 29(3):471–481.

Mitchell, C. N. and Spencer, P. (2003). A three-dimensional

time-dependent algorithm for ionospheric imaging us-

ing GPS. Annals of Geophysics, 46(4):687–696.

Mueller, K., Yagel, R., and Wheller, J. J. (1999). Anti-

aliased three-dimensional cone-beam reconstruction

of low-contrast objects with algebraic methods. IEEE

Transactions on Medical Imaging, 18(6):519–537.

Wang, J., Li, T., and Xing, L. (2009). Iterative image re-

construction for CBCT using edge-preserving prior.

Medical Physics, 36(1):252–260.

ITERATIVE IMAGE RECONSTRUCTION METHODS IN CONE BEAM CT APPLIED TO PHANTOM AND

CLINICAL DATA

553