GENETIC ALGORITHM VERSUS ANT COLONY
OPTIMIZATION ALGORITHM
Comparison of Performances in Robot Path Planning Application
Nohaidda Binti Sariff and Norlida Buniyamin
Faculty of Electrical Engineering, University Technology Mara, Shah Alam, Selangor Darul Ehsan, Malaysia
Keywords: Path Planning Algorithm, Mobile Robot Path Planning, Genetic Algorithm, Ant Colony Optimization.
Abstract: This paper presents the results of a research that uses a simulation approach to compare the effectiveness
and efficiency of two path planning algorithms. Genetic Algorithm (GA) and Ant Colony Optimization
(ACO) Algorithm for Robot Path Planning (RPP) were tested in a global static environment. Both
algorithms were applied within a global map that provides feasible nodes from start point to goal.
Performances between both algorithms were compared and evaluated in terms of computational efficiency
by measuring the speed and number of iterations, accuracy of solution, solution variation and convergence
behavior.
1 INTRODUCTION
Path planning (PP) research covers a wide area of
robotics research that includes PP in static
(Charles.W.Warren, 1993) (Xin, 2005) and dynamic
environments (Mei, 2006) (Stentz, 1994). By
assuming a robot has knowledge of the environment
before it moves, the application of a model based
approach to solve RPP problem in a global static
environment was used in this research.
Examples of traditional approaches proposed by
previous researchers to solve RPP problems are
artificial potential field (Khatib, 1985), neural
network (Xin, 2005), distance wave transform
(Zelinsky, Oct 1993), heuristic algorithm known as
A* algorithm (Charles.W.Warren, 1993) (Hart et al.,
1968), and D* algorithm (Yahja, 2000). It has been
proven in various researches that these algorithms
were able to find global path successfully and that
the various methods has its own strengths and
limitations over others in certain aspect of path
planning.
Recently, due to the evolution of PP algorithms
(PPAs), researchers are viewing RPP problem as an
optimization problem (Sariff, June 2006). This
newer method focuses on finding an optimal path
from start to destination point while satisfying the
optimization criteria for the robot path, such as a
short path with small computation time. In order to
solve the PP problem, the applications of artificial
technologies (Netnevitsky, 2002) itself have been
expanded by utilizing approaches such as
Evolutionary Computation; Genetic Algorithm
(N.Sivanandam, 2008) (Nagib, 2004) (Tu, 2003)
(Ramakrishnan, 2001) and Swarm Intelligence; Ant
Colony Optimization (Dorigo, 2004) (Dorigo and
Gambardella, 1997) (Gengqian et al., 2005) in RPP
research areas. Compared to the traditional
approaches, this method provides robust and
effective search techniques for optimization
purposes which were widely used to solve the RPP
problem.
Since its appearance in 1975 (Goldberg, 1994),
GA has been used in solving many RPP
optimization problems. GA is a search technique
inspired by biology where it works based on the
principle of the fittest of the chromosomes. With its
ability to work with parallel search techniques, the
use of GA contributed to the success of many RPP
research. For example, (Nagib, 2004) proposed the
use of GA to find robot path based on a map of free
space nodes. (Sugihara, 1997) and (Ramakrishnan,
2001) also proposed the used of GA with different
encoding techniques to ensure GA can find optimal
path without depending on the feasible nodes given
in the map. (Hu, 2004) modified classical GA by
incorporating the domain knowledge into specialized
operator to improve GA performances when it works
in environments that consists of obstacles. Previous
125
Binti Sariff N. and Buniyamin N. (2010).
GENETIC ALGORITHM VERSUS ANT COLONY OPTIMIZATION ALGORITHM - Comparison of Performances in Robot Path Planning Application.
In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 125-132
DOI: 10.5220/0002892901250132
Copyright
c
 SciTePress

research indicates that GA can be used to solve RPP
in different applications and that the GA process to
find the optimal path is affected by the
representation of the solution, fitness function
evaluation and genetic operators selection.
ACO, compared to GA is a newer optimization
method. Introduced by (Dorigo, 2004) in
approximately 1992, the application of this
algorithm in RPP research increased rapidly as it is a
powerful tool for solving hard combinatorial
optimizations problem. ACO was inspired by
analogy of behavior of real ants, when looking for
foods. (Zheng, 2007) proposed the use of ACO to
find robot path based on map of MAKLINK graph.
(Mei, 2006) combined ACO with Artificial Potential
Field to produced the path planning in dynamic
environment. (Gengqian et al., 2005) have proven
that ACO can find optimal path in their grid map by
proposing its own probability equation. However, a
literature study shows that the application of ACO to
solve RPP problems has not been explored in detail.
The purpose of the research presented herewith
is to examine the performances of ACO and GA in a
given map (Sariff, 2009). The performances of both
algorithm will be evaluated and compared in terms
of computational efficiency, accuracy of solution,
solution variation and convergence behavior. The
goal is to enhance knowledge of optimization
algorithms in RPP research area. In this paper, the
mapping and path planning algorithms construction
is first discussed. Then results and discussions
provided. Finally, a conclusion that compares and
summarizes the performances of ACO and GA is
presented.
2 RESEARCH METHODOLOGY
Figure 1 illustrates the method applied within this
research. The robot environment must initially be
mapped using an appropriate global map (described
in section 2.1 below). This map will create an output
of nodes represented by xy coordinates. Then, GA
and ACO will start to initialize the population of
path using its own approaches from start to goal by
using all the provided nodes including the start, goal
and all intermediate nodes.
Environment
Map
ApplyGA&
ACOalgorithm
Optimalpath
Figure 1: Proposed Method.
During the initialization, the integer number
represented by each node will be used. However,
during the evaluation, the real x-y coordinates will
be used. At the end of the process, the optimal path
will be found.
2.1 Environment Modeling
In this research, a 2D grid map with size 10x10 cm
was used where the free space nodes (white cell)
represents the area the robot can traverse including
the robot size. The obstacles area (black cell)
represents the boundary of obstacles with the safety
region and the yellow grid represents the feasible
free space nodes that can be traversed by the robot
as shown in Figure 2. The feasible free space nodes
have been located and routed randomly within this
grid map by assuming the nodes are the free space
nodes extract from the mapping algorithm itself. By
using this map, the algorithm will start finding a
solution by initializing the population of feasible
path to goal based on the feasible nodes or
unfeasible nodes (need to be added) available as
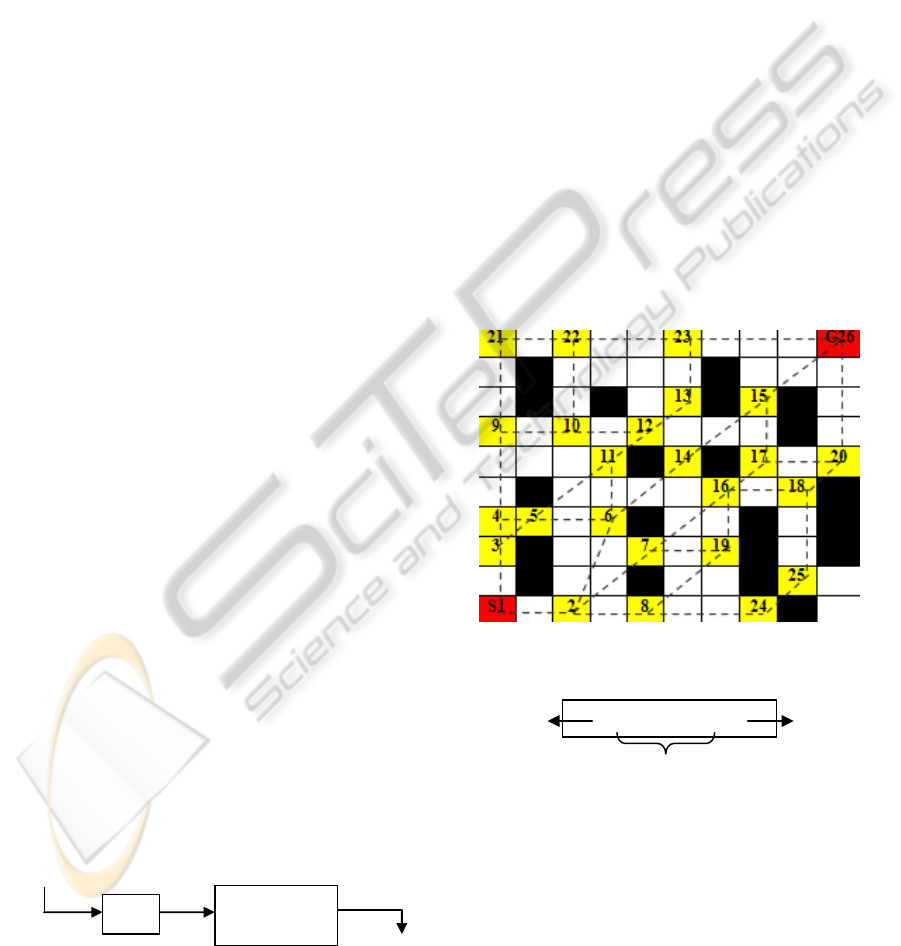
shown in Figure 3.
Figure 2: Global feasible map with 26 free space feasible
nodes.
Start Goal
Feasible and unfeasible nodes
Figure 3: A sample of population consists of feasible
nodes of Figure 2.
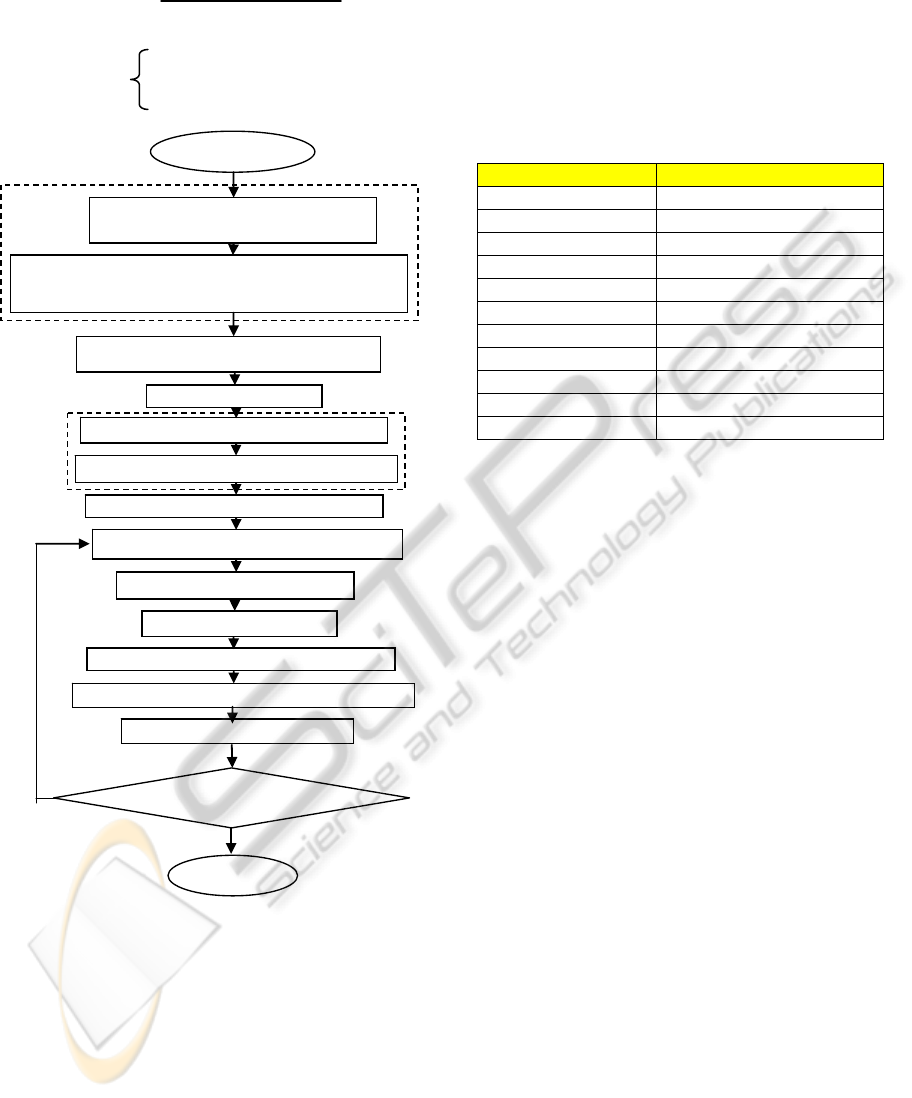
2.2 Genetic Algorithm Design for RPP
The outline of GA is given in Figure 4. The initial
solutions of the RPP problem will initialize in
population randomly. In the first case, the population
will initialize based on the feasible nodes provided
in the global map only. With the complete
1.2.6.14.15
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
126

population, the fitness is evaluated by using the
formula below:
Fitness node=
√
(x2-x1)
2
+ (y2-y1)
2
(1)
Total Fitness= ∑ Fitness node ;Feasi
b
le
(2)
100 ;Unfeasible

Encodetherobotfeasible
Generatepopulationofpathrandomlybased
onrobotfeasiblenodesavailablefromstart
Rankpopulationaccordingtofitness
Selectbestparentswithhighfitness
Du
p
licatebest
p
arentsand
Crossovereachpairofpopulation
Mutateeachpopulation
Firstpopulationisgenerated(Popx)
Newpopulation(Popx”)
Calculatedistances
Rank
p
o
p
ulationaccordin
g
tofitness
Selectbestparentswithhighfitnessvalue
SolutionConverge
No
Yes
START

END
Fitnessevaluation
Figure 4: Outline of GA for RPP of a mobile robot.
After the fitness of each population has been
evaluated, it will be ranked using an elitism
approach. The shorter path will be represented with
a high fitness value and will be selected to be carried
forward to the next generation while the long path
represented with a low fitness value will be
eliminated and removed from the population. The
good parents which is carried forward to the next
generation will produce the diversity of population
that consists of a good child from the genetic
operators process. Then this process is repeated until
all of the GA population found the same optimal
path with no difference of the fitness value where
the distance is equal to 0. It is at this moment, that
the solution converges. The type of GA and
important parameters specifications related with GA
used in this experimental research is defined in
Table
1 below:
Table 1: GA Parameter Specifications.
GA properties Properties
Type of GA Classical GA
Chromosomes type Fixed length chromosomes
Population Size 50
Chromosomes length 15
Selection type Elitism
Crossover type Two point crossover
Mutation type Flip bit
Crossover rate 0.75 of the population size
Mutation rate 0.75 of the population size
Convergence Criteria Max-min of 20 pop≤0.001
Maximum Iteration 40
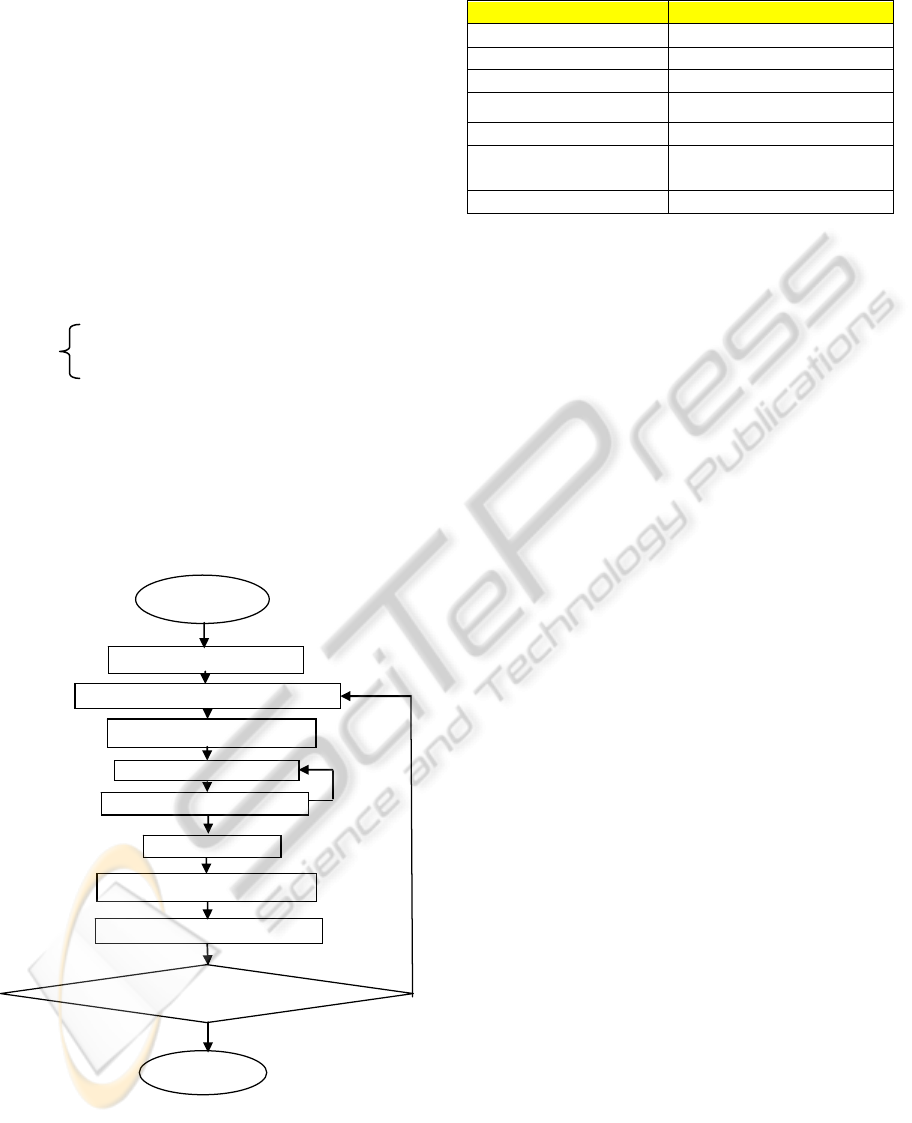
2.3 Ant Colony Optimization Design
for RPP
ACO algorithm used in this experiment is the Ant
System (AS) algorithm as proposed by (Dorigo,
2004). However, a new heuristic equation of state
transition rules is proposed for the RPP purposes.
The evaluation fitness and ACO parameter setting
was created based on the requirements of this
research.
The design of AS for RPP was divided into three
important rules which are state transition rules, local
update rules and global update rules. At the
beginning, ants will determine the next node to be
visited by using the state transition rules based on
heuristic and pheromone laid down by the ants as
shown in derivation below:
Probability ij=heuristic* pheromone
(3)
=[(1/distance between vector start to subpath and
start to perpendicular subpath with reference goal)
β
*
(trail/Σ trail)
α
]
*β=heuristic coefficient,α=pheromone trail coefficient
An accurate value of distance by heuristic
equation and the higher amount of pheromone of the
visited node will be obtained by the ants that have
higher probability to choose that nodes. Within these
rules, ants can balance between the exploration and
exploitation from the relatives coefficient provided,
known as alpha and beta. During the construction of
GENETIC ALGORITHM VERSUS ANT COLONY OPTIMIZATION ALGORITHM - Comparison of Performances in
Robot Path Planning Application
127

the path, the pheromone will be reduced locally by
the given evaporation rate by using the formula of
update local rules below:
Τij (new trail) ←(1-ρ)* τij (old trail), (4)
* ρ=evaporation rate
After all the ants complete the path to goal, then
the process of global updating is applied where ants
will deposits its pheromone based on the path
distance.
tij ← tij + Σ Δ tij
k
(5)
Δ t
ij
k
= amount pheromone of ant m deposits on the
path it has visited. It’s defined as below:
∆ t
ij
k
= Q/C
k
;if arc (i,j) belongs to path P
k
(6)
0
;otherwise
where Q is number of nodes and C
k
is the length of
path P
k
built by the ants.
The amount of pheromone will continuously be
updated until it attracts more ants from the next
generation to follow the shorter path. Finally, the
optimal robot path is found by using behavior of
ants’ concept as shown in Figure 5 below.
Convergencecondition
END
Initializeparameter
Yes
START
Generatestartpointandgoalpoint
Applystatetransitionrules
Movetothenextnode
Allantsreachthegoal
Evaluatefitness
ApplyGlobalUpdatingRule
No
Yes
ApplyLocalUpdatingRule
Figure 5: Outline of ACO for RPP of a mobile robot.
The parameter specifications of ACO utilized in
this experiment is shown in Table 2.
Table 2: ACO Parameter Specifications.
ACO Properties Properties
Population of ants 50 (same as GA)
Length of ants junction 15 (same as GA)
Pheromone coefficient, β 5
Heuristic coefficient, α 5
Evaporation rate, ρ 0.5
Convergence condition Max-min of 20 pop≤0.001
(same as GA)
Maximum Iteration 40 (same as GA)
2.4 Experiment
The method described is then translated and coded
into MATLAB source code by using an appropriate
function available within MATLAB 7.0.4. The
simulation was carried out using a computer with
Intel (R) Celeron (R) M processor 1.5 GHz with
504MB of RAM. Various Simulation results were
then recorded based on the evaluation criteria
required for experiment outcomes such as optimal
path, path cost, time, number of iterations, etc.
3 RESULTS & DISCUSSIONS
3.1 Comparison of GA and
ACO Computational Efficiency
The computational efficiency of both algorithms was
measured by observing the computation time and
number of iteration found by algorithms in 5 test
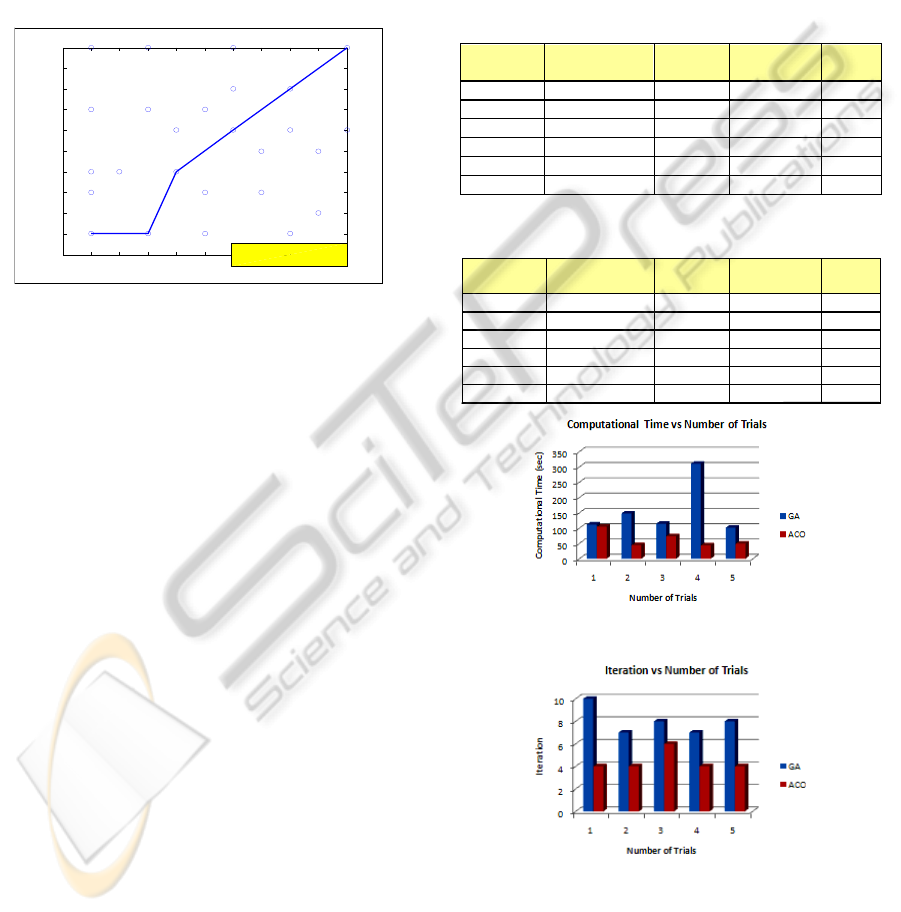
runs. The optimal path found by both algorithms is a
path with connection of feasible nodes
1.2.6.14.15.26 as shown in Figure 6 below with the
path cost that is equal to 13.648 cm. The average
time and iteration value is illustrated in Tables 3 and
4 below while Figures 7 and 8 below have been
proposed to differentiate the values between both
algorithms in each run time.
Based on results tabulated in Tables 3 and 4
below, the average time required by ACO to find the
optimal path (in 5 test runs) is smaller compared to
GA which shows that ACO can perform faster than
GA. The computation time found by ACO in each
run time is mostly less than 100 seconds while GA
run times are in general more than 100 seconds with
the highest run of more than 300 seconds. One of the
factors that influence the increment of time and
iteration is the population being initialized. The way
ACO initializes the population by using a state
transition rules is more efficient compared to GA
that is based on random approaches. With the
efficient derivation of state transition rules, ants
N
o
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
128

capable to determine the next node to be visited near
the optimal node which will produce the population
of ants that traverse near the optimal path to goal.
During this process, ants will choose the nodes with
high probability value (near the optimal node) and
abandon the nodes with low probability value (far
from optimal node). The effect of this process is that
the number of optimal path from one generation to
the next generation will increased rapidly and will
simultaneously drive ACO to converge faster than
GA.
0 1 2 3 4 5 6 7 8 9 10
0
1
2
3
4
5
6
7
8
9
10
Optimal robot path found by Genetic Algorithm
X-Coordinates
Y-Coordinates
START
S1
GOAL
G26
Optimal path =1.2.6.14 .15.26
Distance = 13.648 cm
2
8
24
25
3
4
5
6
719
16
14 17
18
20
1513
12
11
10
9
21 22 23
Figure 6: Optimal path found by GA in 1
st
test run.
However, with the GA, there is no rules to
determine the optimal node as GA uses the random
based approach. This will cause the number of
optimal path in each generation increase in
constantly because population of optimal path is
keep changing depends on the random process itself.
Therefore as results, GA needs more time and
iteration compared to ACO in order to face with the
difficulties of this random approach.
In addition, the way both algorithms carry
forward the optimal path from one generation to the
next generations will also influence the time and
iteration the algorithms require to converge. ACO
will carry forward the updated pheromone values
each time it return back to the start point after it
reach the goal point. The pheromone value carried
by the ants is depending on the selected path traverse
by the ants itself where this value will guide the next
ants to choose the path for the next generations.
Effect from the efficient local and global updating
process, ACO shows the rapid increment of optimal
path population in each generation which will drive
ACO to converge faster compared to GA.
Vice versa with ACO, GA will select the good
population (good parent) which have the highest
fitness to be carry forward to the next generation.
After that, this population will be duplicated and it
will go through some of the process known as
crossover and mutation to produce the next child.
However, because the process to cross and mutate
will also determine randomly so the chances to get a
good child from a good parent also become difficult
and inconstant. Therefore, the increment of optimal
path population in each generation is also not rapidly
increase like ACO where it need more time and
more generations to find the optimal path to goal.
This has been proven in results illustrated in Tables
3 and 4 below where the average time and iteration
in five test run times for ACO is smaller compared
to GA.
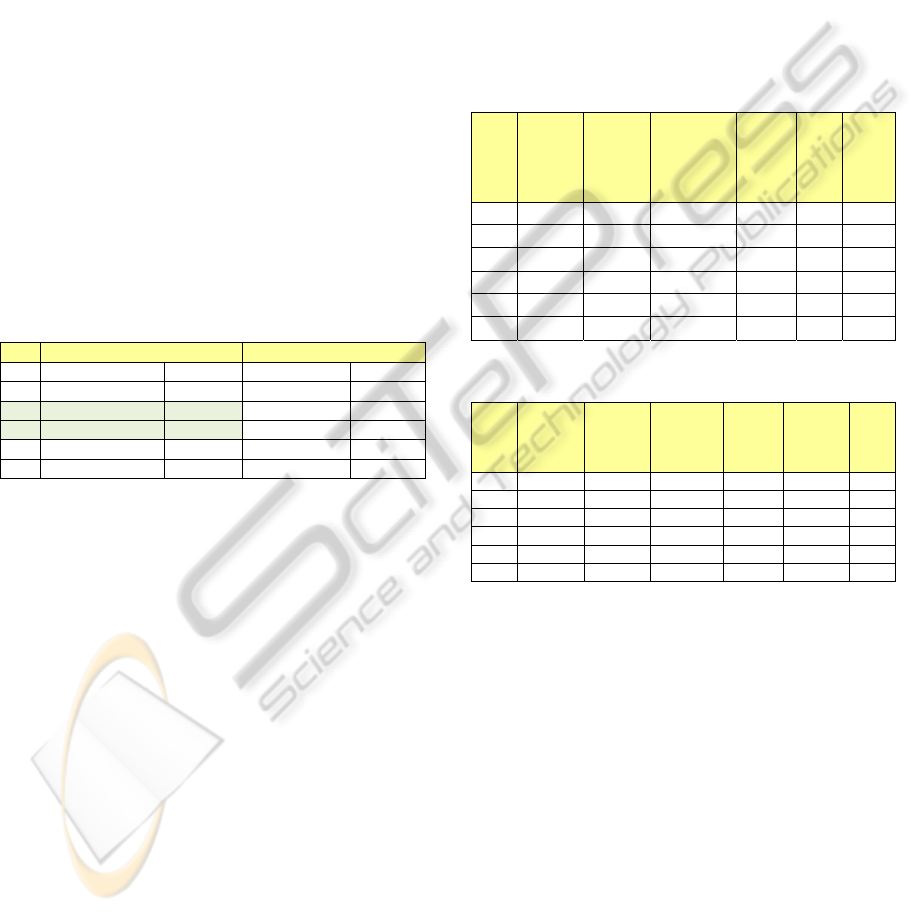
Table 3: Computation Time & Iteration of GA.
Number
of run
Optimal path Distance
(cm)
Time(sec) Iterat
ion
1 1.2.6.14.15.26 13.648 111.838 10
2 1.2.6.14.15.26 13.648 147.958 7
3 1.2.6.14.15.26 13.648 114.362 8
4 1.2.6.14.15.26 13.648 310.464 7
5 1.2.6.14.15.26 13.648 101.278 8
Avg Total 13.648 157.18 8
Table 4: Computation Time & Iteration of ACO.
Number
of run
Optimal path Distance
(cm)
Time(sec) Iterat
ion
1 1.2.6.14.15.26 13.648 104.606 4
2 1.2.6.14.15.26 13.648 44.4 4
3 1.2.6.14.15.26 13.648 73.552 6
4 1.2.6.14.15.26 13.648 43.635 4
5 1.2.6.14.15.26 13.648 49.297 4
Avg Total 13.648 63.098 4.4
Figure 7: GA and ACO computation time.
Figure 8: GA and ACO iteration.
3.2 Comparison of GA and
ACO Accuracy of Solutions
The accuracy of the solution provided by both
algorithms in finding the optimized path can be
GENETIC ALGORITHM VERSUS ANT COLONY OPTIMIZATION ALGORITHM - Comparison of Performances in
Robot Path Planning Application
129

measured from the quality of the path found in each
test run times. The path is optimal if the path is
complete, feasible (not obstruct by obstacles, from
start to finish point), shorter and require small
computation time. For this comparison purposes, the
path based on results is tabulated in Table 5 below.
As depicted, in 5 test runs, ACO could generate
100% of optimal path in 5 test runs while only 60%
of optimal path was generate by GA in 5 test runs.
This shows that ACO can work effectively because
the optimal path found each time the solution
converge. However it was different with GA where
affect from the random process, it will somehow
cause GA to converge although it still in premature
solution. Thus will cause the path being produced is
not optimal, not feasible and not complete to goal as
example shown in the 2
nd
and 3
rd
test run in Table 5
below. Although the path cost is less compare to
other run time, it was still not considered as an
optimal path because the path is not feasible and not
complete to goal. As a result, there are only 3 test
runs among 5 test runs that GA can obtained optimal
path which is equal to 13.648 cm distance.
Table 5: Optimal Path Found by GA & ACO.
GA ACO
No Optimal path Distance Optimal path Distance
1 1.2.6.14.15.26 13.648 1.2.6.14.15.26 13.648
2 1.3.5.11.12.13.26 13.5431 1.2.6.14.15.26 13.648
3 1.2.7.16.17.26 13.5431 1.2.6.14.15.26 13.648
4 1.2.6.14.15.26 13.648 1.2.6.14.15.26 13.648
5 1.2.6.14.15.26 13.648 1.2.6.14.15.26 13.648
3.3 Comparison of GA and
ACO Solution Variation
The fitness of the path population will be evaluated
after the population being initialized at initial stage
of both algorithm processes. This fitness value
represents accumulate data of distance obtained in
each generations and can be used to determine the
solution variation of both algorithms. This achieved
by measuring the different between the maximum
and minimum distance in each generation or by
calculating the mean and standard deviation of the
path distance in the generations itself. Table 6 and 7
tabulated below illustrates the reading of the
maximum distance, minimum distance, differences
between max and min distance, mean and standard
deviation of the distance in 5
th
test runs. The reading
of the distance is referring to the fitness value of the
1
st
population obtained at the 1
st
generation of the
algorithm process.
Based on the results found, average distances
between maximum and minimum value of ACO is
smaller compared to GA which is in ratio 1:9 or
equal to 3 and 45. This is because ACO consists of
accurate and robust initialization approach that
capable to drive ants in the next generation to choose
path which is near the optimal path while abandon
the path which is far from the optimal path. This
process then will affect the range of distance to be
optimized by ACO in each generation is smaller
compared to GA. Therefore, ACO can converge
faster and the number of iteration also will be
reduced. Table 7 above illustrate the range of
distance found by ACO in the 1
st generation which is
differs from GA.
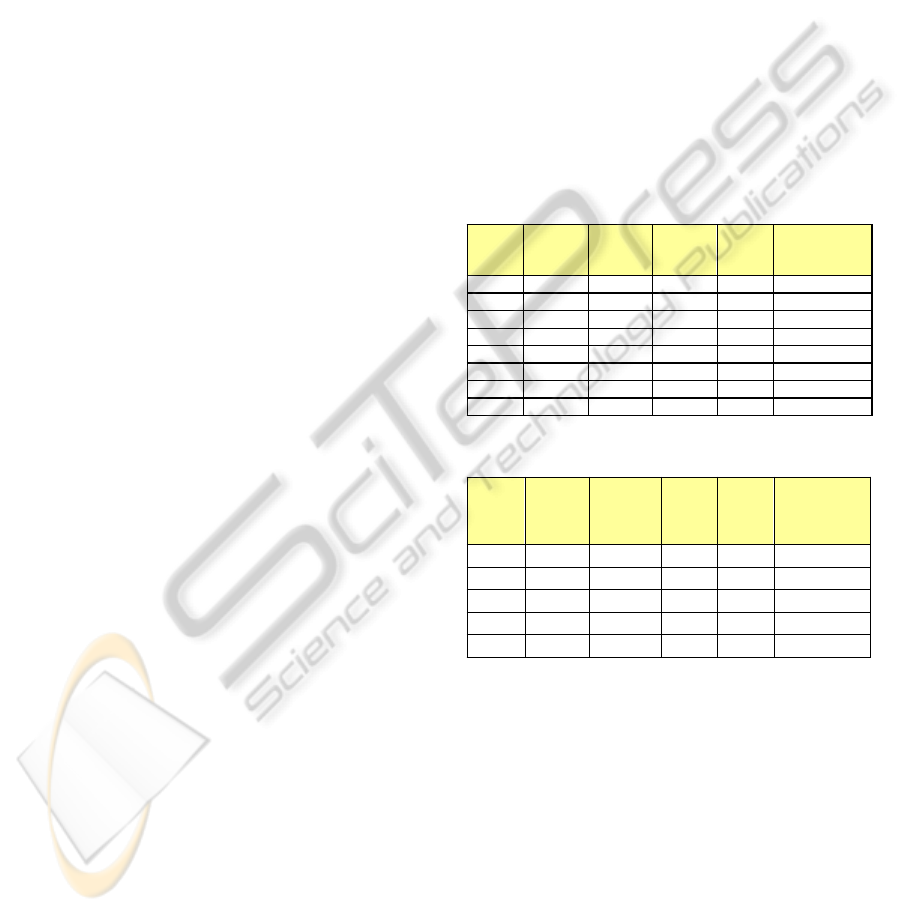
Table 6: Fitness Value of GA Populations.
Num
ber
of
run
Max
distance
Min
distance
Difference
s (Δ max-
min)
Mean,
µ
Sd,
δ
Itera-
tion
1 58.03 13.65 44.382 22.99 0.22 10
2 60.45 13.65 46.799 23.06 0.31 7
3 58.36 13.65 44.712 22.92 0.26 8
4 60.45 13.65 46.799 23.09 0.31 7
5 58.34 13.65 44.692 22.89 0.26 8
Avg 59.126 13.65 45.477 22.99 0.27 8
Table 7: Fitness Value of Ants Populations.
Num
ber
of
run
Max
distance
Min
distance
Difference
s
(Δ max-
min)
Mean
, µ
Sd, δ Itera-
tion
1 18 13.65 4.352 13.781 0.00008 4
2 17.42 13.65 3.766 13.733 0.00004 4
3 17.42 13.65 3.766 13.835 0.00012 6
4 18 13.65 4.352 13.883 0.00028 4
5 14.49 13.65 0.837 13.723 0.00003 4
Avg 17.066 13.65 3.415 13.79 0.00011 22
For GA, there is no rules has been used to
initialize the population where it based on random
approaches. Effect from this process, the population
in the initial generations will consists of optimal and
non optimal path that will generate variety values of
distance. This will cause the range of distance to be
optimized by GA is bigger than ACO. Moreover,
although GA will carry forward the optimal path to
the next generation during the selection process, the
possibility to obtain the population consists of non
optimal child will repeated again. This is because the
point to cross and mutate the chromosomes also will
determine randomly and thus cause to the increment
of the optimized data. As a result, it shows that the
random initialization process of GA from one
generation to other generation had cause GA to
optimize the wide range of distance. Thus will also
cause to the increment of time and iteration GA ta-
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
130

kes to find optimal solution.
The calculation of mean and standard deviation
of the path distance of the 1
st
iteration in each test
runs has been used to verify the range of distance
optimized by both algorithms. Based on the results
found in Tables 6 and 7 above, the value of the mean
and standard deviation of ACO is smaller compared
to GA. With the value of standard deviation of ACO
which is approximate to 0, it can be proven that
population of AC0 are mostly consists of optimal
path population because the data to be optimized is
in a small range and near to 0 compared to GA. As a
result, ACO will work efficiently and meet the
convergence earlier compared to GA.
3.4 Comparison of GA and
ACO Convergence Behavior
The efficiency of both algorithms to find optimal
path during convergence time can be measured by
observing the increment number of optimal path to
goal in each generations as results tabulated in Table
8 and 9 below. In this experiment, the solution
converge when the differences between maximum
and minimum fitness of 20 of the 1
st
population is
equal or less than 0.0001 (≤0.0001). This means that
the algorithm will continuously repeat its process
until the solution meets the requirement of the
convergence that will drive the algorithm to stop its
process.
Based on the results found, GA capable to find
optimal path and converge around 215.361 sec in 7
th
iteration while ACO around 104.606 sec in 4
th
iteration. In GA, the increment of the optimal path
population is slow and steady. 3 optimal paths found
at initial stage of the random process which then
followed by 4,5,7,13,17 and finally reach more than
20 population at the moment the solution converge
at the 7th iteration. It was different with ACO where
the number of optimal path population is increasing
rapidly due to efficient rules provided. Start with 8
populations at the first place then continues with 11,
13 and finally 20 population in 4th times of iteration.
From here, it has been proven that the number of
optimal path increment from one generation to other
generation also can be used to differentiate
performances between both algorithms. ACO is the
robust and efficient techniques compare to GA
where it will not only increase optimal path rapidly
but it capable to trigger itself to find the path faster
with only a small number of iteration. The sufficient
amount of population required for ACO to converge
is the range of data to be minimized is in a big range
as easy to found compared to GA.
Besides that, the change of the range of distance
in every generation also shows the efficiency of both
algorithms reach the convergence solution. In ACO,
the data to be optimized is decreased constantly and
rapidly proportional to the increment of the number
of population in each generation. This has been
proven with the value of maximum distance, mean
and standard deviation that will continuously
decreasing until the solution converge at 4
th
generation as shown in Table 8 above. At the last
generation where the solution converges, the value
of mean is equal to the value of optimal path
distance while the standard deviation is equal to 0
which shows that the solution converges efficiently.
During this moment, ants will follow the same path
and the path distance traverse by ants also become
similar and the solution will reach convergence
easily in a small computation time and a small
number of iteration.
Table 8: GA converge at 7
th
generation.
Iterat
ion
Mean,
µ
Sd, δ Max Min Number of
optimal
population
1 15.843 0.096 18 13.65 3
2 25.749 3.661 54.477 13.65 4
3 29.147 6.005 57.69 13.65 5
4 26.469 4.109 60.447 13.65 7
5 24.699 3.053 57.189 13.65 13
6 24.328 2.852 56.617 13.65 17
7 17.226 0.32 52.503 13.65 27(converge)
Avg 23.352 20.096 50.989 13.65 7
Table 9: ACO converge at 4
th
generation.
Iterat
ion
Mean,
µ
Sd, δ Max Min Numberof
optimal
population
1 13.956 0.002 18 13.65 8
2 13.805 0.0005 14.49 13.65 11
3 13.713 0.00008 13.90 13.65 13
4 13.648 0 13.65 13.65 20(converge)
Avg 13.781 0.0006 15.01 13.65 13
It was different with GA where the data of
distance in each generation will keep changing and
not constantly decreased like ACO. This is because
the way this algorithm remains and increases the
optimal path population in each generation was
based on the random approaches. Effect from this
random process, the population may consists of
population of optimal or non-optimal population that
consists variety amount of distance that will
simultaneously contribute to inconstant distance
value in each generations. With this inconstant
value, the range data to be optimized in each
generation cannot be predicted where sometimes it
will converge in a small computation time and
iteration if the range of data is small while
GENETIC ALGORITHM VERSUS ANT COLONY OPTIMIZATION ALGORITHM - Comparison of Performances in
Robot Path Planning Application
131

sometimes it need a long time and more iteration to
converge if the range of data to be minimized is in a
big range as results shown in Table 9 above.
4 CONCLUSIONS
The research indicates that GA and ACO were able
to find an optimal path in feasible global static
environments. The results show that for the selected
environments, ACO has the capability to work more
efficiently and more accurately than GA. This is
because the computation time and iteration takes to
find the optimal path is smaller. In addition, the
optimal path found in each time run shows the
accuracy of ACO. Furthermore, the range of data to
be optimized is also smaller compared to GA which
will also drive ACO behaviour to converge efficient
and effectively. However, the advantages and
limitations of both algorithms can be further
explored to expand the applications of both
optimization algorithms in RPP research area.
ACKNOWLEDGEMENTS
The authors gratefully acknowledge University
Technology MARA, Malaysia (UiTM) for
supporting this research.
REFERENCES
Charles.W.Warren (1993) Fast path planning using
modified A* Method. IEEE Transactions on
Systems,Man and Cybernetics.
Dorigo, M. & Gambardella, L. M. (1997) Ant colony
system: A Cooperative Learning Approach to the
Traveling Salesman Problem(TSP). Evolutionary
Computation, IEEE Transactions on.
Dorigo, M., Stutzle T (2004) Ant Colony Optimization,
The Bradford Book,The MIT Press
Cambridge.Masachusetts, London, England.pp 1-305.
Goldberg, D. (1994) Genetic and evolutionary algorithms
come on age. Proceedings of Communications ACM,
37, 113-119.
Gengqian, Tiejun L, Yuqing L, P. & Xiangdan P, H.
(2005) The ant algorithm for solving robot path
planning problem. Third International Conference on
Information Technology and Applications, 2005.
ICITA 2005,4-9
Hart, P. E., Nilsson, N. J. & Raphael, B. (1968) A Formal
Basis for the Heuristic Determination of Minimum
Cost Paths. Systems Science and Cybernetics, IEEE
Transactions on, 4, 100-107.
Hu, Y., X.Yang S (2004) A Knowledge Based Genetic
Algorithm for Path Planning of Mobile Robot.
Proceedings of the 2004 IEEE International
Conferences on Robotics and Automation New Oriens,
4350-4355.
Khatib, O. (1985) Real time obstacle avoidance for
manipulators and mobile robots. International Journal
of Robotics Research, 5(10), 90-98.
Mei, H., Tian Y,Zu L (2006) A Hybrid Ant Colony
Optimization Algorithm for Path Planning of Robots
in Dynamic Environment. International Journal of
Information Technology, 12,No 3, 78-88.
N.Sivanandam, S., N.Deepa S (2008) Introduction to
Genetic Algorithms, Springer-Verlag Berlin
Heidelberg 1-425.
Nagib, G., Gharieb W (2004) Path planning for a mobile
robot using Genetic Algorithm. IEEE Proceedings of
Robotics 185-189.
Netnevitsky, M. (2002) Artificial Intelligence:A guide to
intelligent Systems, 2nd Edition, Addison-Wesley.
Ramakrishnan, R., Zein Sabatto S (2001) Multiple Path
Planning for a Group of Mobile Robot in a 2D
Environment using Genetic Algorithms. IEEE
Transactions of Robotics and Systems, 65-71.
Sariff, N., Buniyamin N (2009) Comparative Study of
Genetic Algorithm and Ant Colony Optimization
Algorithm in Global Static Environment of Different
Complexities. 2009 IEEE International Symposium on
Computational Intelligence in Robotics and
Automation (CIRA 2009), Daejeon, Korea, 132-137.
Sariff, N., Buniyamin N (June 2006) An Overview of
Autonomous Robot Path Planning Algorithms. 4th
Student Conference on Research and Development
(Scored 2006), 184-188.
Stentz, A. (1994) Optimal and Efficient Path Planning for
Partially-Known Environments. In Proceedings IEEE
International Conference on Robotics and
Automation, 1-8.
Sugihara, K., Smith.J (1997) GA for adaptive motion
planning of an autonomous mobile robot. Proc. 1997
IEEE International Symposium on Computational
Intelligence in Robotics and Automation (CIRA '97),
138-143.
Tu, J., X.Yang.S (2003) Genetic Algorithms Based Path
Planning for a Mobile Robot. Proceedings of the 2003
IEEE International Conference on Robotics &
Automation, Taipei, Taiwan, 1221-1226.
Xin, D., Hua-Hua C and Wei Kang G (2005) Neural
Network and Genetic Algorithm Based Global Path
Planning in A Static Environment. Journal of Zhejiang
University Science, 6A, 549-554.
Yahja, A., Singh S, Stenz A (2000) An efficient on-line
path planner for outdoor mobile robot. Journal of
Robotics and Autonomous Systems 32, 129-143.
Zelinsky, A., Yuta S (Oct 1993) A unified approach to
planning, sensing and navigation for mobile robots.
Third International Symposium on Experimental
Robotics Kyoto, Japan, 28-30.
Zheng, T. G., Huan H, Aaron S (2007) Ant Colony
System ALgorithm for Real Time Globally Optimal
Path Planing of Mobile Robots. ACTA AUTOMATICA
SINICA, 33, 279-285.
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
132