A STATISITICAL SHAPE MODEL FOR DEFORMABLE

SURFACE REGISTRATION

Wei Quan, Bogdan J. Matuszewski and Lik-Kwan Shark

Applied Digital Signal and Image Processing (ADSIP) Research Centre

University of Central Lancashire, Preston PR1 2HE, U.K.

Keywords: Deformable Registration, Surface Matching, Shape Modelling and Face Articulation.

Abstract: This short paper presents a deformable surface registration scheme which is based on the statistical shape

modelling technique. The method consists of two major processing stages, model building and model

fitting. A statistical shape model is first built using a set of training data. Then the model is deformed and

matched to the new data by a modified iterative closest point (ICP) registration process. The proposed

method is tested on real 3-D facial data from BU-3DFE database. It is shown that proposed method can

achieve a reasonable result on surface registration, and can be used for patient position monitoring in

radiation therapy and potentially can be used for monitoring of the radiation therapy progress for head and

neck patients by analysis of facial articulation.

1 INTRODUCTION

The registration of 3-D surfaces can be considered

as a subset of the general image registration problem

as surveyed by Maintz and Viergever (Maintz and

Viergever, 1998), and has been for many years of

great interest to computer vision community

(Audette et al., 2000). Its applications include

biomedical modelling (Vrtovec et al., 2004),

automated segmentation of medical images

(Lamecker et al., 2003), integrating multiple range

scans into a 3-D model (Hahnel et al., 2003), visual

navigation (Zhang, 1994) and recognition of objects

from database (Lu et al., 2006), etc. In general,

surface registration can be partitioned into three

major components: choice of transformation model,

similarity measure, and optimization method.

The first component concerns the assumptions

made about the relation between the surfaces which

need to be registered. Transformation models can be

roughly classified into two categories, rigid and

deformable. A general rigid transformation can be

expressed as a superposition of rotation and

translation. Deformable transformation could be

similarity, affine, perspective, B-spline, radial basis

function, etc (Audette et al., 2000). The second

component determines what type of characteristic

needs to be extracted from 3-D surfaces. Generally,

the spectrum of surface characteristics includes

landmarks, curves, regions, and dense point sets.

Landmarks are well-localised, sparse loci of

important geometric significance (Thirion, 1994).

Landmarks are frequently determined using

computed surface curvatures or are selected

manually. Curve features typically consist of

differential structures which are usually extracted

from ridges or boundaries between two different

regions in the surfaces (Maintz et al., 1996). Region

features are defined by the areas processing some

homogeneous characteristics, such as consistent

curvature signs (Toriwaki and Yokoi, 1988). Dense

point sets are the feature which constitutes all or

significant subset of all available surface points

(Besl and McKay, 1992). The third component is

about finding parameters of the transformation

which could maximise the similarity measure. This

usually includes the search for the correspondence of

surface characteristics which are used for measuring

the similarity of surfaces. Some frequently used

methods are the random sample consensus

(RANSAC) (Chen et al., 1999), expectation

maximization (EM) (Granger et al., 2001), various

ICP algorithms (Hahnel et al., 2003), etc.

In this paper, a novel method for deformable

surface registration is proposed based on the

authors’ previous work (Quan et al., 2009), which

uses the statistical shape modelling technique to

achieve the deformable registration. The whole

545

Quan W., J. Matuszewski B. and Shark L. (2010).

A STATISITICAL SHAPE MODEL FOR DEFORMABLE SURFACE REGISTRATION.

In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 545-549

DOI: 10.5220/0002895705450549

 SciTePress

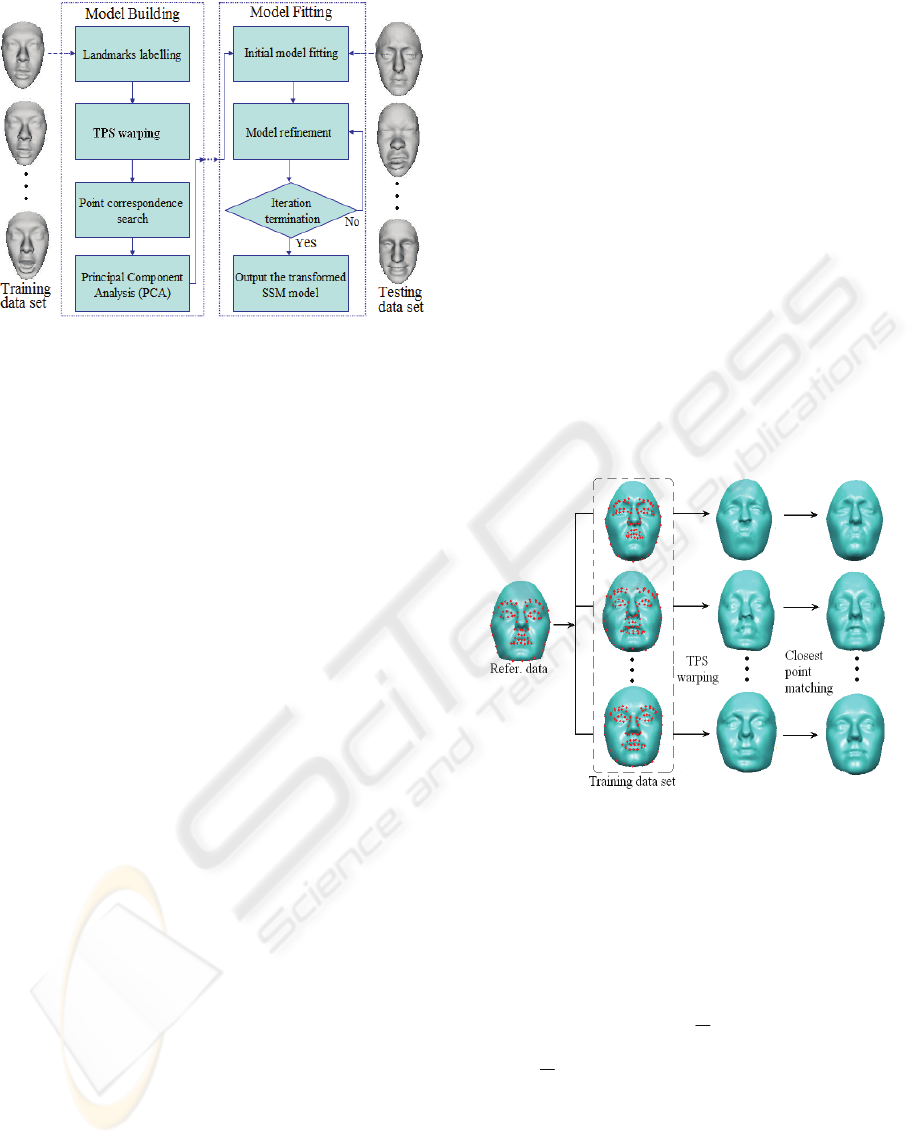
Figure 1: A general framework of proposed surface

registration method.

registration contains two main processing stages:

model building and model fitting, as illustrated in

Figure 1. In the model building stage, all data in the

training set are aligned together. Subsequently the

correspondences of point between each training data

are established, and a statistical shape model (SSM)

is constructed by applying the principal component

analysis (PCA) technique. In the model fitting stage,

the built SSM is roughly aligned with the new data

followed by the iterative model refinement using a

modified ICP algorithm. The proposed method is

applied to facial surfaces in BU-3DFE database (Yin

et al., 2006) that are captured from real persons. This

can be considered as an assessment tool for facial

articulation. Authors believe that it can be used for

monitoring the progress of radiation therapy for head

and neck patients on a daily bases.

The remainder of this paper is organised as

follows. Section 2 describes details of construction

of the SSM. Section 3 explains the procedure of

model fitting process. Finally, concluding remarks

are given in Section 4.

2 MODEL BUILDING

The SSM is developed based on the point

distribution model (PDM) which was first proposed

by Cootes et al. (Cootes et al., 1995), and it is one of

the most widely used techniques for data

registration. Building a statistical shape model is the

first processing stage of the proposed surface

registration method, which involves two phrases of

calculation, estimating dense point correspondence

and PCA. In the following subsections, the model

building is generally introduced.

2.1 Estimating Point Correspondence

The knowledge of the dense point correspondence

between data in the training set is essential, since the

incorrect correspondence can either introduce too

much variation or illegal instance of the model. In

this work, the estimation of correspondence is

achieved in three steps: (i) landmarks determination,

(ii) thin-plate spline (TPS) warping, and (iii) closet

point matching. The first step is to identify the

corresponding landmarks on the selected reference

data and other training data. The second step is to

warp the reference data to different training data

using TPS transformation that is calculated based on

the selected landmarks as control points. The last

step is to estimate the point correspondence between

warped reference data and different training data

based on the closest distance metric. Figure 2 shows

the framework of computing the dense point

correspondences for all training data.

Figure 2: Framework of point correspondence estimation

for the training data set.

2.2 Principal Component Analysis

Having the estimated point correspondences for all

training data, a statistical shape model can be built

using standard PCA, and approximately represented

using a linear model of the form

Q=Wb+Q

(1)

where

Q is the mean vector of all training

data,

[,... ]

Wuuis a so called “Shape Matrix” of

K eigenvectors which correspond to the K largest

eigenvalues , and

[ ,..., ]

b is the shape space

vectors (SSV) which controls the contribution of

each eigenvector that are calculated by PCA, in the

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

546

Figure 3: From top to bottom: superposition of the mean

vector and weighted first three principal components. In

each case the principal component weights vary between

± .

approximated surface

Q . The details of PCA

deduction can be found in (Quan et al., 2009).

Figure 3 shows the effect of varying the first three

largest principal component of the SSM which is

built using 450 training data from BU-3DFE

database.

3 MODEL FITTING

Model fitting is an iterative surface matching

process which includes the estimation of both pose

and shape parameters of the built SSM. Whilst the

pose parameters contain a translation vector, a

rotation matrix and a scaling factor, the shape

parameters are defined by the SSV. As described in

the following subsections, the algorithm starts by

aligning a new data with the mean vector of SSM

using similarity transformation. Subsequently the

model continues to be refined by iteratively

estimating the SSV and pose parameters.

3.1 Initial Alignment

The purpose of initial alignment is to generally

match the SSM to the new data without deforming

itself. The ICP scheme (Besl and McKay, 1992) and

similarity transformation are used together to

achieve the alignment, which iteratively refine the

alignment by alternatively estimating point

correspondence and finding the best similarity

transformation that minimises a cost function

between the corresponding points. In this work the

cost function is defined using Euclidean distance

()

=−+

∑

qRqt

(2)

where

q and ( 1,..., )

q are respectively the

corresponding points from the model and the new

data.

R is a rotation matrix, t is a translation vector

and

is a scaling factor. They can be calculated

directly following the algorithm in (Umeyama,

1991). Figure 4 shows some intermediate results

obtained during the initial alignment.

Figure 4: Some intermediate results obtained during the

initial alignment.

3.2 Model Refinement

The objective of the model refinement is to deform

the model so that it is better matched to the new data

after the initial alignment. This requires for a further

optimisation of the pose parameters as well as the

shape parameters, which can be seen as a

superposition of the ICP method and the least

squares projection onto the shape space. The least

squares projection onto the shape space provides the

SSV,



, which controls the deformations of the

model. The SSV,



b , for an new data is calculated

from



()

b=W Q +Q

(3)

where

R∈Q is a vector which contains

corresponding points representing the new data.

The mean vector of all training data

and shape

matrix

W are computed through the PCA as shown

in Equation 1.

From Equation 3, it can be seen that the size

(dimension) of SSV is fixed during iterations of

model refinement. Using the fixed size of SSV

A STATISITICAL SHAPE MODEL FOR DEFORMABLE SURFACE REGISTRATION

547

Figure 5: From left to right: new data, corresponding SSM

using fixed large size of SSV, and corresponding SSM

using fixed small size of SSV.

can usually provide a reasonable final result of

refinement if a good initial alignment is achieved.

Otherwise, it may mislead the minimization of the

cost function for the model refinement towards a

local minimum, i.e., approximating to an

inappropriate shape. This is because when a large

size of SSV is used, the model will have high degree

of freedom for generating shapes, but with an

incorrect initial alignment this freedom can make the

model approximate to an incorrect arbitrary shape,

which leads to a failure result of the refinement

eventually. On the other hand, although a model

with the small size of SSV has low degree of

freedom, which constraints the deformation

capability of the model and prevents it from

generating an arbitrary shape, it also limits the

model to evolve to the right shape. Figure 5 shows

some failure examples of refinement in which the

sizes of SSV used are fixed.

In order to solve the problem caused by the fixed

size of SSV, the authors proposed a model

refinement process using a SSV with the adaptive

size in this work, and the Equation 3 needs to be

rewritten as



()

b=W Q+Q

(4)

Figure 6: Example of intermediate results obtained during

iteration of the model refinement. The new data which

needs to be matched is shown in Figure 5.

where



b is the SSV with the adaptive size, and

W is the corresponding shape matrix estimated

separately for each k).

indicates level of the

refinement. In the beginning of the refinement SSV

has a small size. Although the registration error can

be very big at this stage, the algorithm is able to

provide rough approximation of the data. When the

registration error is decreased, the size of SSV will

be gradually increased, which provides more shape

flexibility and allows the model to match the data.

Parts of intermediate results of the model refinement

are shown in Figure 6. In the figure, it can be seen

that using the SSV with the adaptive size the model

refinement is able to provide a smooth transition

during the iterations and eventually deform the

model to the right shape even in the case that the

result of initial alignment is not very good.

4 CONCLUSIONS

This paper describes a novel deformable surface

registration method which uses statistical shape

modelling technique and the modified ICP scheme.

In order to avoid the local minima of the cost

function of the model refinement process, a SSV

with the adaptive size is proposed which enables the

SSM eventually converge to the right shape even if

the initial alignment does not provide a reasonable

result. The proposed method is successfully applied

to the real facial data from BU-3DFE database, and

it can model well with different facial shape across

genders, races or expressions. This suggests that the

proposed method can be potentially used for some

associated medical applications, such as the

quantification of 3D face articulation for early

predication and assessment of facial dysfunctions or

the progress monitoring of radiation therapy for head

and neck patients.

ACKNOWLEDGEMENTS

The work presented in this paper has been supported

from the MEGURATH and the TERAFS projects

(EPSRC Project No.EP/D077540/1, EP/H024913/1)

REFERENCES

Audette M F. P.,. A., Ferrie Peters T. M., 2000. An

algorithm overview of surface registration techniques

VISAPP 2010 - International Conference on Computer Vision Theory and Applications

548

for medical imaging, Medical Image Analysis, Vol. 4,

201-217. Elsevier science.

Besl P. J., McKay N. D., 1992. A method for registration

of 3-D shapes, IEEE Trans. PAMI, vol. 14(2), 239-

256.

Chen C. S., Huang Y. P., Cheng J. B., 1999. Ransac-based

darces: a new approach to fast automatic registration

of partially overlapping range images, IEEE Trans.

PAMI, vol. 21(11), 1229-1234.

Cootes T. F., Taylor C. J., Cooper D. H., Graham J., 1995.

Active shape models – their training and application,

Computer Vision and Image Understanding, vol.

61(1), 38-59.

Granger S., Pennec X., Roche A., 2001. Rigid point

surface registration using an EM variant of ICP for

computer guided oral implantology, Medical Image

Computing and Computer-Assisted Intervention, 752-

761.

Hahnel D., Thrun S., Burgard W., 2003. An extension of

the ICP algorithm for modelling nonrigid objects with

mobile robots, Proceeding of the International Joint

Conference on Artificial Intelligence, 1-6.

Lamecker H., Lange T., Seebass M., 2004. Segmentation

of the liver using a 3D statistical shape model, ZIB-

Report 04-09.

Lu X., Jain A., Colbry D., 2006. Matching 2.5D face scans

to 3D models, IEEE Trans. PAMI, vol. 21(12),1357-

1362.

Maintz J. B. A., Van den Elsen P. A., Viergever M. A.,

1996. Evaluation of ridge seeking operators for

multimodality medical image matching, IEEE Trans.

PAMI, vol. 18(4), 353-365.

Maintz J. B. A., Viergever M. A., 1998. A survey of

medical image registration, Med. Image Anal., vol.

2(1), 1-36.

Quan W., Matuszewski B. J., Shark L. K., Ait-Boudaoud

D., 2009. Facial expression biometric using statistical

shape models, EURASIP Journal on Advances in

Signal Processing, vol. 2009.

Thirion J. P., 1994. External points: definition and

application to 3D image registration, Proceeding of

Computer Vision and Pattern Recognition, 587-592.

Toriwaki F. I., Yokoi S., 1988. Voroni and related

neighbours on digitised two-dimensional space with

application to texture analysis, Computational

Morphology.

Umeyama S., 1991. Least-square estimation of

transformation parameters between tow point

patterns, IEEE Trans. on VCG, vol. 13(4), 376-380.

Vrtovec T., Tomazevic D., Likar B., Travnik I., Pernus F.,

2004. Automated construction of 3D statistical shape

models, Image Anal Stereo, vol. 23(1), 111-120.

Yin L., Wei X., Sun Y., Wang J., Rosato M., 2006. A 3D

facial expression database for facial behaviour

research, International Conference on Automatic Face

and Gesture Recognition, 211-216.

Zhang Z., 1994. Iterative point matching for registration

of free-form curves and surfaces, International

Journal of Computer Vision, Vol. 13(2), 119-152.

A STATISITICAL SHAPE MODEL FOR DEFORMABLE SURFACE REGISTRATION

549