IDENTIFICATION OF AREAS WITH SIMILAR WIND

PATTERNS USING SOFM

J. C. Palomares Salas, A. Agüera Pérez, J. J. G. de la Rosa and J. G. Ramiro

Research Unit PAIDI-TIC-168, University of Cadiz, Electronic Area, Escuela Politécnica Superior

Avda. Ramón Pujol, S/N. E-11202-Algeciras-Cádiz, Spain

Keywords: Cluster Analysis, Clustering Applications, Data Mining, Self-Organizing Feature Map.

Abstract: In this paper it is shown a process to demarcate areas with analogous wind conditions. For this purpose a

dispersion graph between wind directions will be traced for all stations placed in the studied zone. These

distributions will be compared among themselves using the centroids extracted with SOFM algorithm. This

information will be used to build a matrix, letting us work with all relations simultaneously. By permutation

of elements in this matrix it is possible to group relationed stations.

0B1 INTRODUCTION

Clustering is a method of unsupervised learning, and

a common technique for statistical data analysis

used, the majority of times, in data mining, machine

learning, pattern recognition, image analysis,

bioinformatics or dimension reduction. However, in

many such problems, there is a little prior

information (e.g., statistical models) available about

the data, and the decision-maker must make as few

assumptions about the data as possible. It is under

restrictions that clustering method is particularly

appropriate for the exploration of interrelationships

among the data points to make an assessment

(perhaps preliminary) of their structure.

This method is used when to compile and

classify by hand is expensive, and the

characterization of the patterns change with time. On

the other hand, lets to find useful characterization to

build classifiers, and the discovery of class and

subclass that to reveal the nature of the problem

structure.

There are many clustering techniques; the most

widely used are hierarchical clustering and dynamic

clustering (Xiaozhe, 2006). The first are the called

clustering tree and is one of the most widely used

clustering approaches due to the great visualization

power it offers. Hierarchical clustering produces a

nested hierarchy of similar groups of objects,

according to a pairwise distance matrix of the

objects. One of the advantages of this method is its

generality, since the user does not need to provide

any parameters such as the number of cluster.

However, its application is limited to only small

datasets, due to its quadratic computational

complexity. The second is the well knows k-means.

While the algorithm is perhaps the most commonly

used clustering algorithm in the literature, it does

have several shortcomings, including the fact that

the number of clusters must be specified in advance.

Both of these clustering approaches, however,

require that the length of each time series is identical

due to the Euclidean distance calculation

requirement, and are unable to deal effectively with

long time series due to poor scalability. As in

supervised classification methods, there is not

clustering technique that is universally applicable.

The demarcation of different zones with

connected wind patterns could have an important

contribution to prediction models based on data

acquired in meteorological stations placed in the

studied area. When these models are based on the

statistical learning of data (Neural Networks,

ARMAX, Genetic Fuzzy Learning…), the inclusion

of not correlated or erroneous stations can

destabilize the process of obtaining the desired

knowledge.

In this article, we will use the self-organizing

feature map (SOFM) clustering analysis technique to

classify zones with similar wind patterns. The main

reason of to apply this algorithm is the capability of

the learning by example held in SOFM model (Kun-

Lin, 2007). One time that this first clustering has

been realized, we propose a new method based on

Genetic Algorithms for to optimize the final

classification of the study zone.

Palomares Salas J., Agüera Pérez A., J. G. de la Rosa J. and G. Ramiro J. (2010).

IDENTIFICATION OF AREAS WITH SIMILAR WIND PATTERNS USING SOFM.

In Proceedings of the 12th International Conference on Enterprise Information Systems - Artiﬁcial Intelligence and Decision Support Systems, pages

40-45

DOI: 10.5220/0002896300400045

 SciTePress

1B2 AREA AND WIND DATA

In this work the daily mean wind speed and direction

of 88 met stations, from 2005 to 2008 have been

used. The map of the region and the location of these

stations are depicted in Fig. 1. These stations are

distributed over 87000 Km

and they are orientated

to measure agriculture variables (Red de

Información Agroclimática). In this way, wind

records have not enough reliability because, despite

of the most of them are located in open zones, the

anemometer height is 1,5 m and is highly affected

by obstacles and ground effects. (This fact add value

to this study because this kind of meteorological

records are more frequent than the good ones, and is

interesting to build a structure that allows to use

them in order to the wind resource evaluation.)

3 METHOD FOR

EXPLORATORY DATA

ANALYSIS

There exist several methods for quickly producing

and visualizing simple summaries of data sets. A

main goal in the field of exploratory data analysis is

to extract useful information out of large and usually

high-dimensional data sets. In the past, clustering

large datasets has been a domain of classical

statistical methods. More recently a new approach,

Kohonen's Self Organizing Feature Map (SOFM)

has been proposed in order to classify high

dimensional datasets, while having no analogous

traditional method for unsupervised data analysis

(Varfis, 1992).

As new approaches from the field of

connectionism were presented, those were compared

to classical methods and similarities among them

were said to be found. In particular the Kohonen

algorithm was said to be similar to the k-means

method, as it is stated, that the SOFM method is

closely related or a partitioning method of the k-

means type (Murtagh, 1995). The SOFMs aren’t

identical to k-means type and in some cases

outperform a variety of classical statistical

approaches.

3.1 The Self-organizing Map

Algorithm

Kohonen‘s Self-Organizing Feature Maps represent

one very well known and widely used Neural

Network Model which employs unsupervised

learning. This means that the result is formed by the

properties inherent to the data itself; there is no

master who tells what is true or false. So no previous

knowledge about the structure of the data is needed

to be able to use the algorithm.

Self-organizing feature maps (SOFM) learn to

classify input vectors according to how they are

grouped in the input space. They differ from

competitive layers in that neighboring neurons in the

self-organizing map learn to recognize neighboring

sections of the input space. Thus, self-organizing

maps learn both the distribution (as do competitive

layers) and topology of the input vectors they are

trained on.

Figure 1: Map showing the location of meteorological

stations.

The basic SOM consists of M neurons located on

a regular low dimensional grid, usually 1 or 2

dimensional. The lattice of the grid is hexagonal,

rectangular or random, see Fig. 2.

The neurons represent the inputs with reference

vectors m

, the components of which correspond to

synaptic weights. One reference vector is associated

with each neuron called unit in a more abstract

setting. The unit, indexed with c, whose reference

vector is nearest to the input x is the winner of the

competition:

(

)

{

}

minarg

mxxcc −==

(1)

Usually Euclidean metric is used, although other

choices are possible as well.

The winning unit and its neighbours adapt to

represent the input even better by modifying their

reference vectors towards the current input. The

amount the units learn will be governed by a

neighbourhood kernel h, which is decreasing

function of the distance of the units from the

winning unit on the map lattice. If the locations of

units I and j on the map grid are denoted by the

IDENTIFICATION OF AREAS WITH SIMILAR WIND PATTERNS USING SOFM

Figure 2: Topologies for the original neuron locations: (a) rectangular lattice, (b) hexagonal lattice, (c) random lattice.

two- dimensional vectors r

and r

, respectively, then

()

(

)

trrhth

jiij

;−= , where t denotes time.

During the learning process at time t the

reference vectors are changed iteratively according

to the following adaptation rule, where x(t) is the

input at time t and c = c(x(t)) is the index of the

winning unit:

( ) () () ()

(

)

[]

tmtxthtmtm

iciii

−+=+1 (2)

In practice the neighbourhood kernel is chosen to

be wide in the beginning of the learning process to

guarantee global ordering of the map, and both its

width and height decrease slowly during learning.

The learning process, consisting of winner

selection by equation 1 and adaptation of the

synaptic weights by equation 2, can be modelled

with a neural network structure in which the neurons

are coupled by inhibitory connections.

The main properties of such self-organizing

maps can be stated as (Ritter, 1989):

- The distance relationships between the input

data are preserves by their images in the map as

faithfully as possible. While some distortion is

unavoidable, the mapping preserves the most

important neighbourhood relationships between

the data items, i.e., the topology of their

distribution.

- The map allocates different numbers of nodes

to inputs based on their occurrence frequencies.

If different input vector appear with different

frequencies, the more frequent one will be

mapped to larger domains at the expense of the

less frequent ones.

4 PROPOSED PROCEDURE FOR

TO CLUSTER STATIONS

USING SELF-ORGANIZING

FEATURE MAPS (SOFM)

The following procedure has been executed to

demarcate areas with similar wind patterns:

4.1 Characterization of Stations

To characterize the measurement stations, wind

directions (WD) of all them have been chosen for

two random days to yield a vector of dimension

2x88. Once we have obtained this vector the SOFM

algorithm has been carried out. The SOFM module

in MATLAB 7.7.0 has been used to be our tool of

analysis. The configurations parameters related to

the implementation of SOFM by MATLAB 7.7.0

software were as follows: size of layer dimension, [2

5]; network topology, ‘hextop’; distance function,

‘linkdist’. With these parameters we perform the

training of the network to obtain the weights of the

network. Figure 3 shows the scatter plot of this

vector together with the initial weights of the

network and the finals weights of the network after

training.

Figure 3: SOFM Training.

ICEIS 2010 - 12th International Conference on Enterprise Information Systems

Once the network has been trained we come back to

choose two random days and is simulated with

the obtained network configuration. The following

are make a note of what cluster each station belongs.

This process is repeated 373 times with what a

matrix of size (88x373) is obtained to end. After this

matrix is obtained, it is possible to determine how

many times two stations have been inserted en the

same cluster.

4.2 Matrix of Similarities

Once all stations are characterized by the position of

the weights of the network it is possible to establish

a parameter which indicates the degree of similarity

(DS) between two distributions. We propose (3) the

calculation of the mean distance between each

neuron, C, and the nearest one belonging to the

distribution of the other station, C’

. Thus, the lower

is the value of DS, the higher is the similarity of

both distributions.

∑

−

(3)

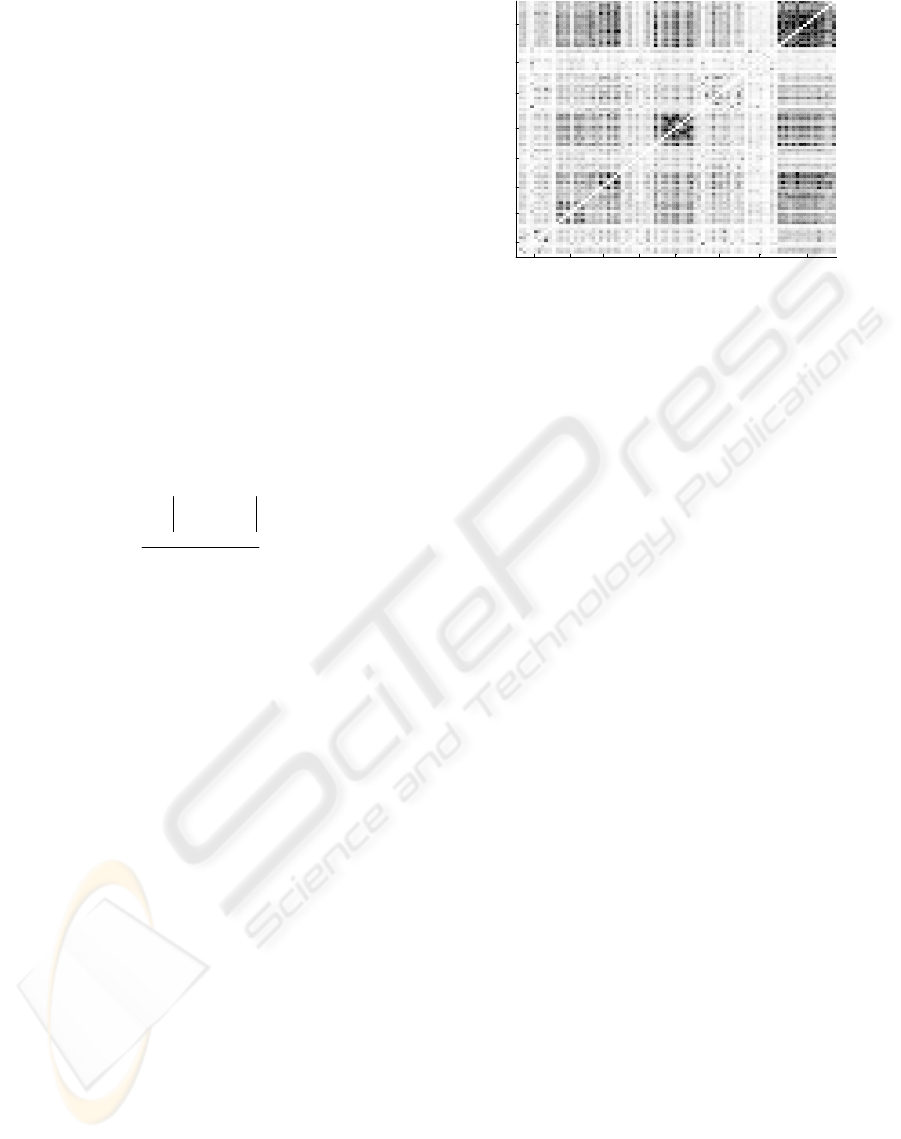
Calculating this parameter for all possible pairs

of stations, the matrix DS (composed of DS

) can be

constructed. This matrix contains the relations

among all the wind patterns measured at the stations,

and it can be represented as figure 4 shows, grouped

by provinces. The order of grouping of the provinces

is Almería (Alm), Cádiz (Cad), Córdoba (Cor),

Granada (Gra), Huelva (Hue), Jaen (Jae), Málaga

(Mal), and Sevilla (Sev). The dark pixels are

associated to a low value of DS; therefore, they

connect stations with similar patterns. Thus, the

white cross observed over Málaga (Mal) stations

indicates that the most of them have not relations

with other stations, even if they are placed in the

same province. On the contrary, Huelva (Hue)

shows strong relations among the stations installed

in the area. Córdoba (Cor) presents the same pattern

in almost all the province, but this pattern is repeated

in Sevilla (Sev), as it is possible to infer from the

dark areas connecting these provinces. This fact

indicates that the classification of the stations

according to their provinces is not the best in order

to visualize the areas with a similar wind patterns.

The actual order of the matrix comes from

alphabetical and administrative criteria, but these

considerations have not relation with the concerned

problem, the wind classification. If the stations were

grouped according to the relations among them, by

Alm Cad Cor Gra Hue Jae Mal Sev

Alm

Cad

Cor

Gra

Hue

Jae

Mal

Sev

Figure 4: Representation, greyscale, of the matrix

composed of the values of DS for each pair of stations.

permutation of rows and columns of the matrix, the

relations and clusters could be clarified.

5 GENETIC ALGORITHMS

Genetic algorithms (GAs) have been recognized as

powerful approaches to solving optimization

problems. They are search algorithms based on

natural genetic and selection combining the concept

of survival of the fittest with a structured

interchanges, but aleatory of the information. These

concepts involve the preservation of the

characteristics of the best exponents of a generation

in the next generation; moreover introducing

aleatory changes in the new generation composition

by means of crossing over and mutation operations

(Lorena, 1997). One of the main advantages of GA

in opposite to the traditional search methods is that

this aleatory component prevents getting stuck into a

local maximum from which you can not escape to

reach a global maximum. Other advantage is its

utility of real time applications, in spite of not

providing the optimal solution to the problem it

provides almost the better solution in a shorter time,

including complex problems to solve by traditional

methods.

5.1 Ordering the Matrix DS with

Genetic Algorithms

Although the permutation of rows and columns to

put in order the DS matrix seems to be a simple

problem; the reality proves that this process could be

compared with a Rubik cube, since the order in a

part of the matrix could involve the disorder in other

one.

The result (or objective) of the recombination of

IDENTIFICATION OF AREAS WITH SIMILAR WIND PATTERNS USING SOFM

rows and columns must be a matrix in which the

stations with similar winds patterns and relations

will be neighbours, that is, the nearby elements of

the obtained matrix must be as similar as possible.

Figures 5a and 5b present two possible

recombination of the matrix represented in figure 4,

being the second one closer to the objective

explained before. To evaluate this idea of order, the

parameter p is proposed in equation 4, where p

, a

and b are constants related to the scale of the

problem. In this case p

= 25000, a = 100 and b =

415.

()

∑∑∑

−==

+⋅⋅=

ijkijkij

BAF

p (4)

−

−=

)(

)( kjiij

ijk

DSDSa

DSDS

kjiij

ijk

)( +

−

Each column, j, which represents a station, is

compared with the six closer columns indexed by

j+k=j-3,...,j,...j+3, calculating two factors with their

i-th elements, A

ijk

and B

ijk

. The resulting value of A

ijk

+ B

ijk

is low when the sum of the elements is high

and the difference low. That is, nearby stations with

high similarities among them and with analogous

relations with the rest of the stations will contribute

with low values to the final result of p. The sum of

all these values, covering all the columns, gives an

objective measurement of the similarities among the

nearby columns and, therefore, an evaluation of the

global order of the matrix. For example the value of

p for the matrix shown in figure 4 is 0.902. As it was

expected, figures 5a and 5b obtain lower values

because they have been ordered in some sense.

Especially the combination represented in 5b

presents a very low value of p (p=0.843) which

indicates a high degree of similarity (or order).

Now the problem of ordering the matrix of

similarities has been reduced to find a combination

of stations with a minimum value of p. We propose

to solve this minimization problem using Genetic

Algorithms (GA). Each matrix of similarities can be

characterized by a vector of 88 elements containing

the position of the stations. This vector could be

considered as a genome which defines univocally

the associated matrix. Furthermore, using the value

of p calculated with these matrixes, a population of

0 20 40 60 80

Figure 5: a) Ordination of stations from sparsely related to

highly related (p=0.854). 5b) Ordination according to

subjective criteria of permutation (p=0.843).

these vectors could be tested and ranked. In these

conditions, GA could improve this population using

evolutive operators as crossover, mutation,

migration, etc., in order to obtain the minimum value

of p (Goldberg, 1989).

As it has been introduced upper, the vectors used

as genome of the matrixes contain 88 elements.

These elements are non repeated integer numbers

between 1 and 88, and each of them is associated to

one of the used stations. The positions of this

numbers in the vector define the position of the

stations in the matrix and, thus, the value of p for

this combination can be calculated. Because of the

properties of the genome used in this work, the

evolutive operator selected to produce the new

generations is the Recombination. Recombination

permutes one or more elements of the genome, thus,

the resulting vector is composed of 88 non repeated

integers again; avoiding the repetitions, decimals

and values out of range given by other operators.

6 RESULTS

The matrix selected by the GA as best combination

of stations, after 1000 generations and a population

of 10

individuals is represented in figure 6. This

0 10 20 30 40 50 60 70 80

Figure 6: Representation, greyscale, of the matrix obtained

after applying the Genetic Algorithm where the main

clusters have been selected with numbered squares.

ICEIS 2010 - 12th International Conference on Enterprise Information Systems

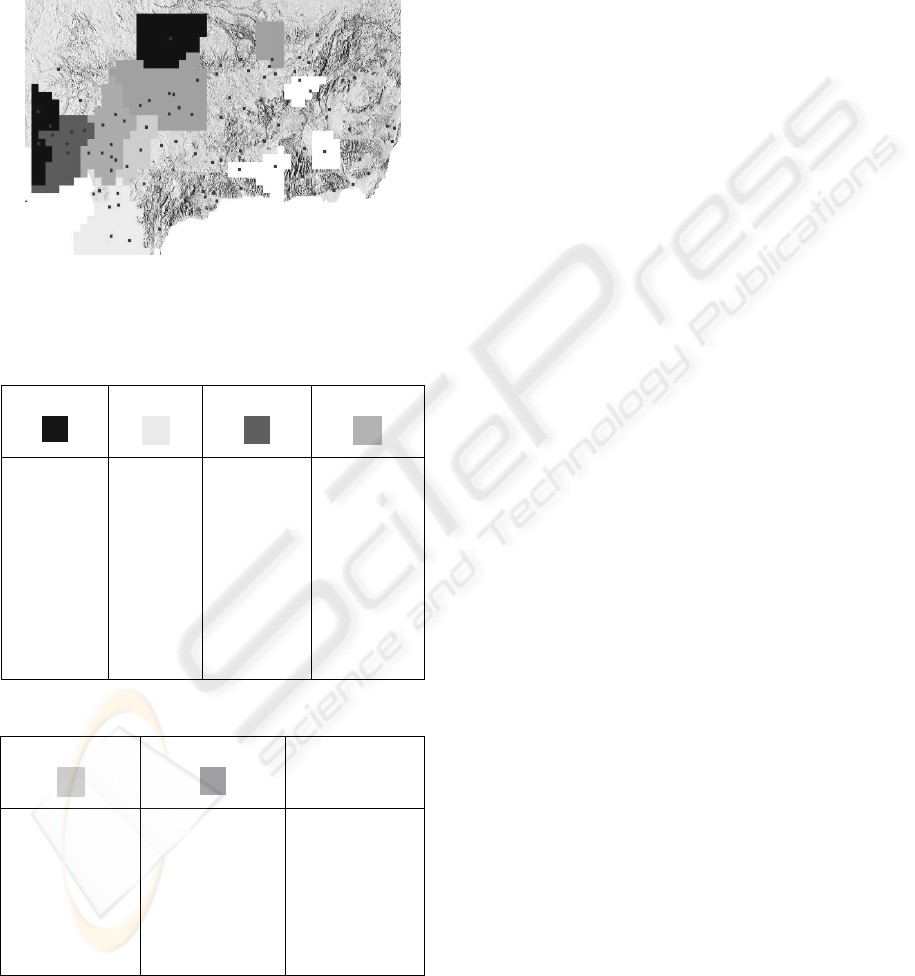
figure depicted the main clusters with squares and

the value of p associated to this matrix is 0.805.

Once we have selected the clusters are

represented in the study area. This is shown in figure

7 where it follows the same colour code. Tables 1

and 2 shows the information of the stations that have

been selected as cluster belongs.

Figure 7: Representation of study zone and the clusters

selected.

Table 1: Names selected stations in the clusters 1, 2, 3 and

Cluster 1

Cluster 2

Cluster 3

Cluster 4

- Puebla

Guzmán

- Bélmez

- Gibraleón

- Lepe

- Conil

- Jerez

- Puerto

Santa Mª

- Vejer

- Basurta

- Moguer

- Cebollar

- Tojalillo

- Niebla

- Palma del

Condado

- Sanlúcar la

Mayor

- Guillena

- Almonte

- Rinconada

- Aznalcázar

- Puebla del

Río

- Lebrija

- Puebla del

Río II

- Isla Mayor

Table 2: Names selected stations in the clusters 5, 6 and 7.

Cluster 5

Cluster 6

Cluster 7

- Tomejil

- Los Molares

- Las Cabezas de

San Juan

- La Luisiana

- Palma del Río

- Écija

- Hornachuelos

- Lora del Río

- Santaella

- Córdoba

- Villanueva

- Linares

- Huesa

- Padul

- Zafarraya

- Fiñana

- San José de los

Propios

7 CONCLUSIONS

The results obtained demonstrate that the proposed

method is able to demarcate areas with analogous

wind patterns, even if the data acquired is affected

by low quality instruments or locations. In the same

way, erroneous stations, or stations not

representative of the wind climate in their zone, will

be identified since they will not be included in any

cluster. So, this tool could be useful in two aspects:

- In first steps of wind resource assessment,

when a preliminary description of the wind

climate in a zone is needed. Then, using the

information given by this matrix, it is possible

to associate the location of the target area with

an expected wind pattern.

- When a wind methodology, as Measure-

Correlate-Predict or the ones used in wind

temporal forecasting, needs support stations to

complete or extend the database used. In this

situation is very important to exclude stations

with errors or not representative of the studied

area because it could lead to important

differences between results and reality.

REFERENCES

Xiaozhe Wang, Kate Smith, Rob Hyndman, 2006.

Characteristic-Based Clustering for Time Series Data.

Data Mining and Knowledge Discovery. vol. 13,

number 3, pp. 335 – 364.

Kun-Lin, H., Cheng-Chang, J., I-Ching, Y., Yan-Kwang,

C., Chun-Nan, L., 2007. The study of applying a

systematic procedure based on SOFM clustering

technique into organism clustering. Expert Systems

with Applications: An International Journal. vol. 33,

pp. 330 – 336.

Varfis, A., Versino, C., 1992. Clustering of Socio-

Economic Data with Kohonen Maps. Neural Network

World. vol. 2(6), pp. 813 – 834.

Murtagh, F., Hernández-Pajares, M., 1995. The Kohonen

Self-Organizing Map Method: an Assessment. Journal

of Classification. vol. 12(2), pp. 165 – 190.

Ritter, H., Kohonen, T., 1989. Self-organizing semantic

maps. Biological Cybernetics. vol. 61, pp. 241 – 254.

Lorena, L.A.N., Lopes, L.S., 1997. Genetic algorithms

applied to computationally difficult set covering

problems. Journal of the Operational Research

Society. vol. 48, pp. 440 – 445.

Goldberg, D.E., 1989. Genetic Algorithms in Search,

Optimization and Machine Learning. Addison–Wesley.

Reading.

IDENTIFICATION OF AREAS WITH SIMILAR WIND PATTERNS USING SOFM