TRAINING A FUZZY SYSTEM IN WIND CLIMATOLOGIES
DOWNSCALING
A. Agüera, J. J. G. de la Rosa, J. G. Ramiro and J. C. Palomares
Research Group PAIDI-TIC 168, University of Cadiz, Ramón Puyol S/N, Algeciras, Spain
Keywords: Wind Climate, Fuzzy Systems, Genetic Algorithm, Topography.
Abstract: The wind climate measured in a point is usually described as the result of a regional wind climate forced by
local effects derived from topography, roughness and obstacles in the surrounding area. This paper presents
a method that allows to use fuzzy logic to generate the local wind conditions caused by these geographic
elements. The fuzzy systems proposed in this work are specifically designed to modify a regional wind
frequency rose attending to the terrain slopes in each direction. In order to optimize these fuzzy systems,
Genetic Algorithms will act improving an initial population and, eventually, selecting the one which
produce the best aproximation to the real measurements.
1 INTRODUCTION
The knowledge of the wind resources available in a
selected area is fundamental to evaluate the possible
installation of wind turbines destinied to produce
electrical energy. The models used in these
evaluations needs high requirements to work and
vagueness in terrain descriptions or errors in
measurements affect considerably the reliability of
the simulation. Hence the majority of information
registered in a studied area, from stations destinied
to agriculture, fire detection or pollution, will be
rejected to be used in these estimations because of
their low quality. A fuzzy wind model could be able
to use all these excluded data reducing the
requirements (and therefore the time and the costs)
of the wind resource prospections.
The most of the numerous works that describe a
mesoscalar wind potential evaluation in different
areas of the world summarize the wind measured at
the stations giving a general view of the wind
conditions (Boehme, 2008). When a higher
reliability is needed, the study is normally based on
Computational Fluid Dynamics (CFD) (Palma,
2008) (Gastón, 2008) . CFD solves the fluid
mechanic equations over a terrain with high
computational cost (especially in this scale), and
losing certainity when complex geography and
chaotic dynamic arises. So, these estimations are
slow and expensive.
Fuzzy Logic, Artificial Neural Networks and other
adaptative tools are statistical structures able to work
with low requirements and high tolerance to possible
errors (Gutiérrez, 2006). Thus, using these
techniques in the wind resource assessment, the data
quality could be replaced with data quantity and the
deterministic prediction with a probabilistic one,
more inline with the atmospheric dynamic (Louka,
2008) (Cellura, 2008).
In this paper, Genetic Fuzzy Learning will be
used to develope a fuzzy system able to transform a
regional wind climate into a local one attending to
basic aspects of the surrounding topography.
2 AREA AND WINDDATA
To illustrate this paper, measurements from a net of
meteorological stations have been acquired. These
stations are focused on agricultural parameters, so
their locations and instruments are not optimized to
the wind resource estimation. As it is shown in
figure 2, the selected station is located at Jimena
(Andalucia, Spain), inmersed in a complex terrain.
The other three neighbor stations, with similar
characteristics, have been collected to build a
regional wind climate.
3 REGIONAL WIND CLIMATE
The regional wind climate, which will be forced by
the terrain conditions, is generated as a linear
238
Agüera A., J. G. de la Rosa J., G. Ramiro J. and C. Palomares J. (2010).
TRAINING A FUZZY SYSTEM IN WIND CLIMATOLOGIES DOWNSCALING.
In Proceedings of the 12th International Conference on Enterprise Information Systems - Artificial Intelligence and Decision Support Systems, pages
238-243
DOI: 10.5220/0002899402380243
Copyright
c
 SciTePress

combination of real data registered at the stations
around Jimena. This combination is based in
interpolation functions for geostatistics variables
(defined by G. Matheron (1963)), and its application
to Atmospheric Sciences suggested by Thiebaux and
Pedder (Thiebaux, 1987). Zekay Sen (Sen, 1998)
have used these works to calculate the monthly
mean wind speed in different areas in Turkye
obtaining good results.
In this paper these techniques are used to
generate a wind frequency rose calculating wind
vectors in a point (v
jimena
) as linear combination of
real wind vectors recorded at the three stations
mentioned before (v
1
, v
2
, v
3
):
332211
vavavav
jimena
r
r
r
r
++=
(1)
The coefficients a
i
are normalized and indicate the
contribution of each station to the final result. This
coefficients will be calculated using studied
geostatistic weighting functions and normalizing:
∑
=
j
j
i
i
rW
rW
a
)(
)(
(2)
Where r
i
represents the distance between Jimena and
the ith station, and W(r
i
) is the weight function
which adopts this form (Thiebaux and Pedder):
⎪
⎩
⎪
⎨
⎧
>
<
⎟
⎟
⎠
⎞
⎜
⎜
⎝
⎛
+
−
=
Rr
Rr
rR
rR
rW
i
i
i
i
i
0
)(
22
22
α
(3)
The parameter α can be changed in order to
modulate the distribution, and R is the radius of
action beyond that the evaluated point does not
contribute. The values of this paramaters (R=50
Km, α=2) have been selected according with
(Agüera, 2009). In this last work, it is possible to
find detailed information of the interpolation system
used here.
The result of this process is a temporal serie of
wind vectors created with real information of the
area. This serie can be analyzed in order to test the
accuracy of the prediction. In figure 1 the real wind
frequency rose at Jimena is compared with the rose
of the regional wind climate generated by linear
combinations of data from stations of the area.
As it is possible to see, the regional wind rose
builded with this method gives an important
aproximation of the real wind measured at the
meteorological station of Jimena. But, in spite of this
general similarity, there is an important difference
when the expected incoming direction is E and the
5
10
15
20
N
S
WE
real
Regional Wind
Figure 1: Real and Regional wind frequency roses.
station measures SE. This is due to the linear
interpolation predicts a theoretical wind whithout
information of topography, roughness, obstacles, etc.
However, the wind measured in a point is affected
by local conditions and these effects may be
evaluated in order to get a better prediction. So
fuzzy systems will be used to transform the regional
wind distribution into the real one evaluating relief
parameters. To achieve this objective, the
geographical information must be processed and
inserted in a matrix builded as it is shown in the
following section.
4 TERRAIN
In figure 2 is represented the process through which
an altimetric map image is transformed in the matrix
used as terrain input in this model. In the altimetric
image each colour is associated to a height above sea
level. Then, reading the RGB components of each
pixel, a height matrix of the area can be created and
represented (figure 2a).
The wind measured in a point could be defined
as a vector whith module and direction equal to wind
speed and wind direction. Hence, the simmetry of
this problem is radial and input arguments should be
expressed in polar coordinates.
Figure 2b shows the mean heights of the digitized
area, fractioned in sectors (M
ij
) depending on the
polar coordinates relatives to the central point
(Jimena).
Each M
ij
is obtained as the mean height of the n
pixels inside the ij-sector (1):
n
rh
M
n
ij
∑
=
),(
θ
(4)
TRAINING A FUZZY SYSTEM IN WIND CLIMATOLOGIES DOWNSCALING
239

Figure 2: Area of Jimena and transformations to obtain the model terrain input from a map image.
-500 0 500
0
0.5
1
slope
Degree of members hi
p
down
plain
up
0 10º 22.5º
0
0.5
1
deviation
low
medium
high
0 0.5 1
0
0.5
1
probability
low
medium
high
Figure 3: Possible description of the input and output domains using the proposed fuzzy sets.
The matrix M, composed of Mij, is represented in
Figure 2c. As it is shown in the graphic explanation
below, each column contains information of one
direction. So a turn in the wind direction will be
interpreted as a displacement in x-axis. M gives an
usefull representation of the physical geography
around the calculation point, adapted to the
simmetry of the problem, and it is easily applied as
input of fuzzy systems.
5 GENETIC FUZZY SYSTEM
The fuzzy system used in this problem pretends to
connect the local wind conditions with terrain
characteristics of the area. The vagueness in the
terrain description in this scale, the quality of data
recorded at the used stations, and the chaotic
dynamics inherent to atmospheric events demand a
fuzzy treatment of these elements. The proposed
system will calculate the probability of possible
changes in the direction of the wind analyzing the
terrain in those directions. In order to simplify the
problem only two inputs parameters will be
proposed: the terrain will be described considering
the “slope” and the wind behavior will be represented
by a “deviation” in the incoming direction. In the
same way, the output parameter will be represented
by “probability”. References (Zadeh, 1997)
(Sanchez, 1997) are fundamental bibliography to
understand and study in depth the concepts used in
this section.
5.1 Fuzzy Sets
Fuzzy Logic is based on the fuzzification of crisp
variables obtaining fuzzy sets, so linguistic terms are
generally used to build the new description. Each
fuzzy set is defined in a domain and it is
characterized by a membership function with values
between 0 and 1 which indicates de degree of
membership of an element to the concerned fuzzy
set. For example, a fuzzyfication of the parameter
“slope”, defined as the difference of heights between
two relief elements in the range [-500m, 500m],
could be done using these fuzzy sets [down, plain,
up]. So the parameter “slope” could be fuzzyficated
as it is shown in Figure 3.
In this figure is also represented a possible election of
fuzzy sets for the parameter “deviation” ,[low,
medium, high], defined between 0 and 22.5 degrees.
“Probability”, whith range [0, 1] will be divided with
three sets [low, medium, high].
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
240

5.2 Fuzzy Rules
Using these fuzzy sets it is possible to to build “IF-
THEN” rules connecting the inputs with the output
generating a knowledge base. For example: IF
“deviation” is high and “slope” is up THEN
“probability” is low.
Now it is possible to map crisp input values into
output ones by using the processes of fuzzyfication,
fuzzy inference and defuzzyfication. So, the fuzzy
systems used in this work can be represented as
follow:
),( dsfuzzp =
(5)
Where s and d are the input values, p is the output
and fuzz represents the processes of fuzzyfication and
inference.
5.3 Genetic Algorithm
The membership functions, and fuzzy rules could be
defined and adjusted by a human expert or founded
using adaptatives tools. In this paper we will try to
optimize the fuzzy system with Genetic Algorithms
(GA).
So, we must encode the fuzzy system characteristics
into a string of values which will be considered a
genome of this system. Mutation and Crossover
operators can act on these strings generating new
fuzzy systems; and a selection operator can select
individuals according to the values obtained from a
fitness function or objective. The action of these
operators brings an iterative process through which
an initial population of fuzzy systems could be
improved in order to obtain the best fitness value. We
have chosen 22 parameters (genes) to characterize
each fuzzy system. Eight of them are relationed with
the position and shape of the memberships functions;
so, they are continous. The other ones are discrete
variables used to build the fuzzy rules of the system
(Table 1).
5.4 Fitness Function
The prove suggested to rank the fuzzy systems
involves the modification of the regional frequency
rose by interaction with M, the matrix which contains
the processed information of the map (Figure 4 c).
This correction of the regional rose will be done
using an iterative process which simulates the wind
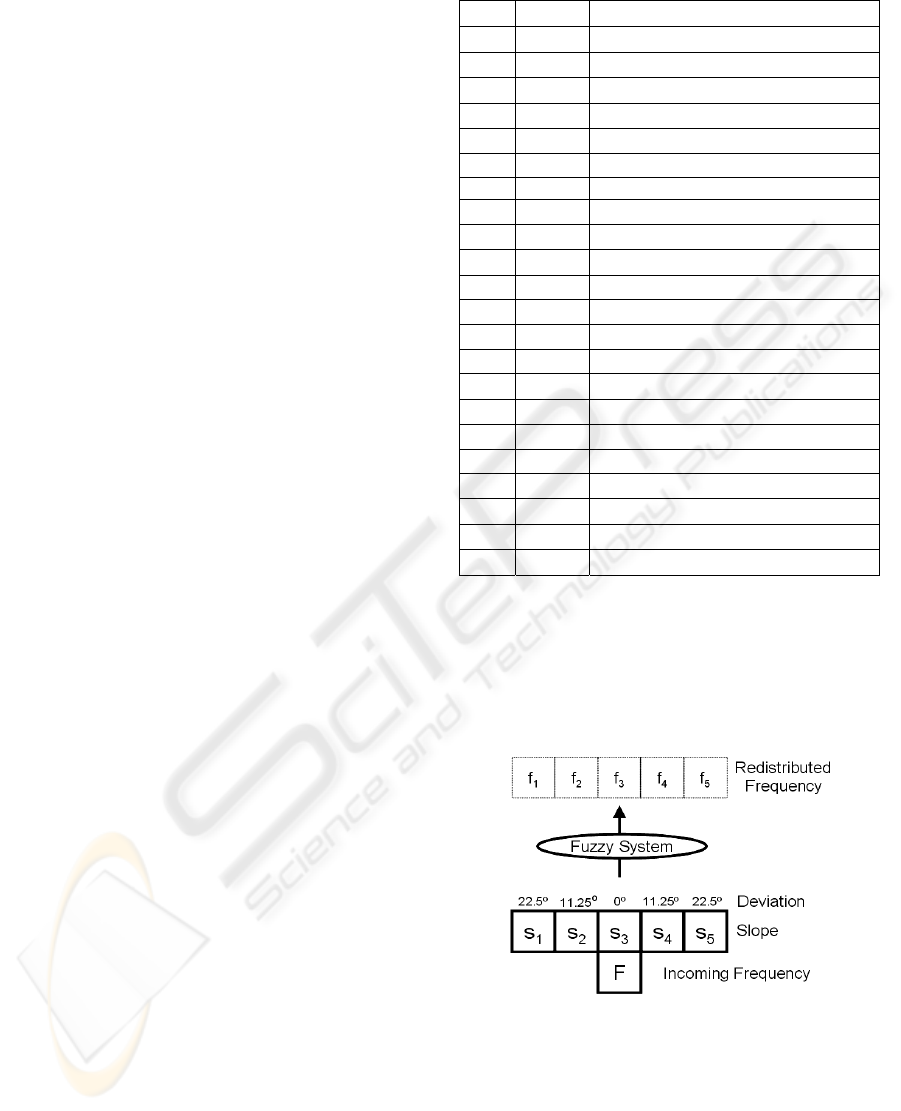
flowing over the matrix M from the bottom up. In
each step the fuzzy system has to distribute the wind
frequency in a selected direction (F) over the five
upper elements attending to the slopes and possible
deviations as figure 4 shows. The iteration of this
Table 1: Genes.
Gen Values Parameter
1 [0, 1] Width Slope / down
2 [0, 1] Width Slope / plain
3 [0, 1] Width Slope / up
4 [0, 1] Position Slope / down
5 [0, 1] Position Slope / plain
6 [0, 1] Position Slope / up
7 [0, 1] Width Deviation / low-medium-high
8 [0, 1] Width Probability / low
9 [0, 1] Width Probability / medium
10 [0, 1] Width Probability / high
11 0, 1, 2 Fuzzy rule 1 / input 1
12 0, 1, 2 Fuzzy rule 2 / input 1
13 0, 1, 2 Fuzzy rule 3 / input 1
14 0, 1, 2 Fuzzy rule 4 / input 1
15 0, 1, 2 Fuzzy rule 1 / input 2
16 0, 1, 2 Fuzzy rule 2 / input 2
17 0, 1, 2 Fuzzy rule 3 / input 2
18 0, 1, 2 Fuzzy rule 4 / input 2
19 0, 1, 2 Fuzzy rule 1 / output 1
20 0, 1, 2 Fuzzy rule 2 / output 1
21 0, 1, 2 Fuzzy rule 3 / output 1
22 0, 1, 2 Fuzzy rule 4 / output 1
process generates diagrams, like the one shown in
figure 7, where probabilistic trajectories induced by
the fuzzy system are represented, and the output
distribution could be considered a corrected rose
obtained from the regional one after the interaction
with the topographic elements.
Figure 4: Corrections of directions using the fuzzy system,
where “Inc” indicates the incoming direction, s
i
and p
i
the
slope and probability in each direction. The deviations
affect the five upper elements because, according to the
fuzzy sets defined before, deviations are limited to 22.5º,
and consecutive elements in a row represent deviations of
11.25º.
TRAINING A FUZZY SYSTEM IN WIND CLIMATOLOGIES DOWNSCALING
241

-500 0 500
0
0.5
1
slope
Degree of membership
down
plain
up
0º 10º 22.5º
0
0.5
1
deviation
low
medium
high
0 0.5 1
0
0.5
1
probability
low
medium
high
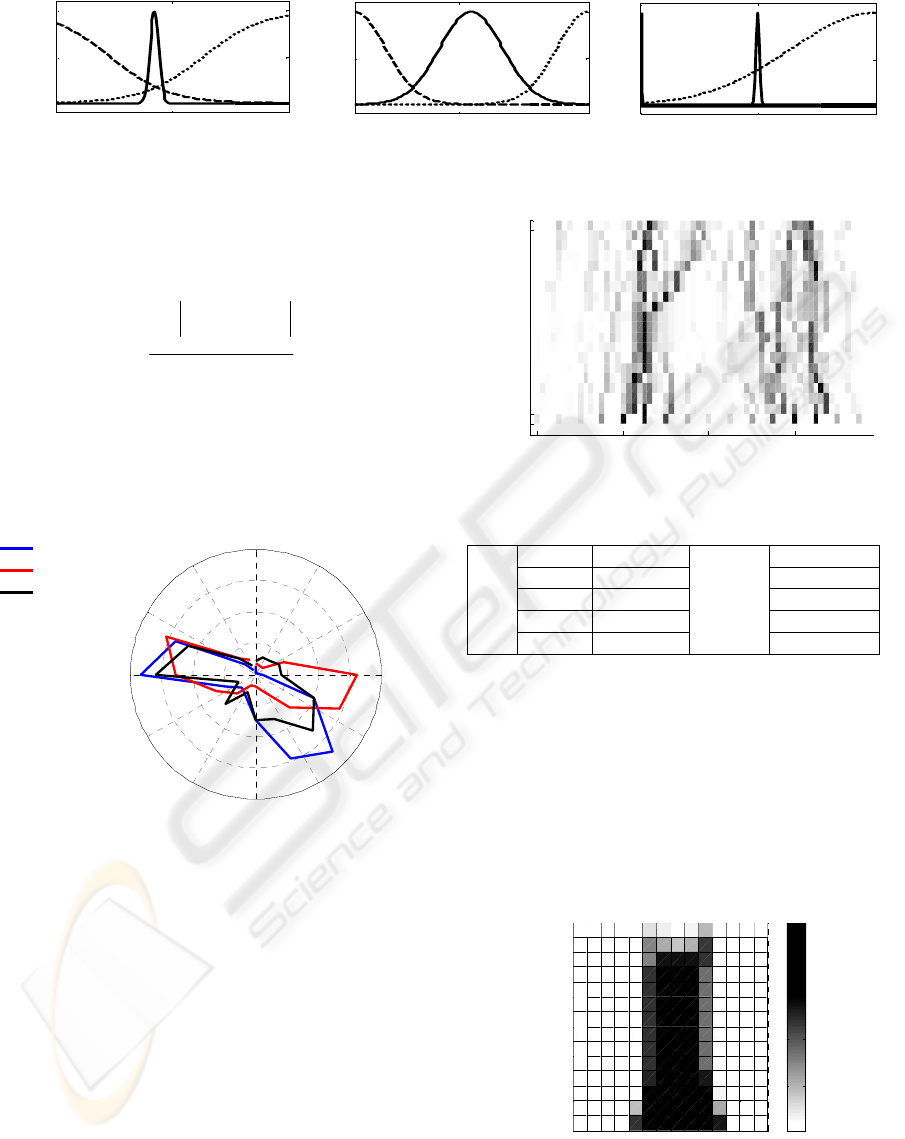
Figure 7: Optimized Fuzzy Sets.
Once the corrected rose is obtained, it will be
compared with the real one evaluating the mean
absolute error (MAE) in each direction:
16
16
1
∑
=
−
=
j
jj
FSFR
MAE
(6)
Where FR represents the real frequencies measured
at Jimena, FS the simulated ones and j is a parameter
that covers the 16 sectors of the roses. MAE value
will be used as a fitness value to rank the fuzzy
systems.
5
10
15
20%
N
S
WE
Real Wind
Regional Wind
Corrected Wind
Figure 5: Real, Regional and corrected roses.
6 RESULTS
After the action of Genetic Algorithms, an optimized
fuzzy system have been obtained. The correction of
the probability distribution given by this fuzzy
system is shown in figure 5. The MAE value
obtained with this distribution is 2.35% that improve
the 4.29% associated to the regional rose. As it was
expected, the probabilistic trajectories simulated by
the trained fuzzy system (Figure 6) describe a strong
modification in the winds from E displaced to the S,
in opposition to the ones from the W which are
smoothly modified. These corrections are derived
from the action of fuzzy rules and fuzzy sets
summarized in table 2 and figure 8.
N E S W
Rose
Input
Rose
Output
Figure 6: Density of trajectories.
Table 2: Fuzzy Rules.
IF
Slope Deviation
THEN
Probability
Plain Medium Medium
Up Medium Low
Down High Low
Plain High Low
The inference surface builded with this information
is showed in figure 8, where slope and deviation are
connected to the output (probability, gray scale). The
fuzzy system associates the highest probability to
medium deviations when the slope is smoothly
negative. Turns higher than 20º and positive and
strongly negative slopes are not favored. Another
minor effect observed is that wind tolerates a wider
range of slopes while flowing in the same direction,
that is, deviation 0º.
-200 -100 0 100
0
10º
22.5º
slope
deviation
0.1
0.2
0.3
0.4
Figure 8: Inference surface.
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
242

7 CONCLUSIONS AND FUTURE
WORK
The fundamental conclusion of this work is that the
described process presents a way to train fuzzy
systems in wind parameters downscaling. It is
clearly visible the improvement of the obtained wind
frequency distribution with regard to the regional
one. This fact implies that the optimized fuzzy
system contains information about how to correct
the wind direction over Jimena using the terrain
slopes. This acquired knowledge is the best
statistical solution founded through Genetic Fuzzy
Learning according to the variables and conditions
imposed to solve this particular problem in this
location. But the ultimate objective of this technique
should be the development of a generalized fuzzy
system able to work in many enviroments and
expanded to correct the wind speed, the most
important variable in wind resource evaluation. In
order to get the best agreement, this system should
evaluate more terrain characteristics as roughness,
heights and distances from obstacles to the target
point, topographic complexity, etc. Despite this
parameter inclusion, this new extended problem is
essentially similar to the one described in this paper.
The differences are related to the number of inputs
and outputs of the fuzzy system and the number and
characteristics of the terrains used in the training
process.
Since fuzzy logic is able to work with vague data, an
interesting application of this technique lies in
training fuzzy systems to work with low quality
stations. In fact, the stations used in this study can be
considered poor, because wind vanes and
anemometers are placed at 2 meters above ground
level and reported data could be affected by
obstacles and roughness. Another problem is that the
frequency of the provided mean wind speed and
direction is daily, far from the recommended ten-
minutes interval. In opposition to these
inconvenients, the use of this information allows to
acquire easily a considerable quantity of long term
time series of real measurements of the area. So,
once this general fuzzy system is obtained, the
duration and requirements of the wind resource
evaluation of large areas could be strongly reduced.
Finally, the technique exposed could be also applied
to all that processes in which wind and terrain are
closely relationed as fire propagation or erosion.
REFERENCES
Boehme, Thomas A.Robin Wallace, Hindcasting Hourly
Wind Power across Scotland Based on Met Station
Data, Wind Energy 2008; 11: 233-244.
Palma, J.M.L.M., F.A. Castro, L.F. Ribeiro, A.H.
Rodrigues, A.P. Pinto; Linear and nonlinear models in
wind resource assessment and wind turbine micro-
siting in complex terrain; Journal of Wind Engineering
and Industrial Aerodynamics 96 (2008) 2308– 2326.
Gastón, Martín, Edurne Pascal, Laura Frías, Ignacio Martí,
Uxue Irigoyen, Elena Cantero, Sergio Lozano,
Yolanda Loureiro; Wind resources map of Spain at
mesoscale. Methodology and validation. Wind Energy
Department, National Renewable Energy Center
(CENER).
Gutiérrez, J. M., Rafael Cano, Antonio S. Cofiño, Carmen
M. Sordo; Redes probabilísticas y neuronales
aplicadas a las ciencias atmosféricas, INM,
Ministerio de Medio Ambiente, Madrid (2006).
Louka, P., G. Galanis, N. Siebert, G. Kariniotakis, P.
Katsafados, I. Pytharoulis, G. Kallos. Improvements
in wind speed forecasts for wind power prediction
purposes using Kalman filtering; Journal of Wind
Engineering and Industrial Aerodynamics 96 (2008)
2348– 2362.
Cellura, M., G. Cirrincioneb, A. Marvuglia, A. Miraouic;
Wind speed spatial estimation for energy planning in
Sicily: A neural kriging application; Renewable
Energy 33 (2008) 1251-1266.
Matheron, G. , Principles of geostatistics, Econ. Geol. 58
(1963) 1246-1266
Thiebaux, H.J., M.A. Pedder, Spatial Objective Analysis
with Applications in Atmospheric Sciences, Academic
Press, New York, 1987, 299 pp.
Sen Zekai, Ahmet Duran Sahin, Wind energy evaluation
in some parts of Turkey, J. Wind Eng. Ind. Aerodyn.,
74-76 (1998) 345-353.
Agüera, A., J. G. Ramiro, J. Melgar, J. J. G. de la Rosa,
J.C. Palomares, A. Moreno. “Categorization of
minimum error forecasting zones using a geostatistic
wind model”; Proceedings Clean Electrical Power
2009 Capri (Italy), IEEE.
Zadeh, Lofti A.; Fuzzy sets, fuzzy logic and fuzzy systems,
Advances in fuzzy Systems – Applications and Theory
vol..6. World Scientific. 1997.
TRAINING A FUZZY SYSTEM IN WIND CLIMATOLOGIES DOWNSCALING
243