
FORMATION CONTROL OF MULTI-ROBOTS VIA SLIDING-MODE
TECHNIQUE
Razvan Solea, Daniela Cernega, Adrian Filipescu and Adriana Serbencu
Control Systems and Industrial Informatics Department, Computer Science Faculty
“Dunarea de Jos” University of Galati, Domneasca 111, 800201, Galati, Romania
Keywords:
Formation control, Sliding-mode control, Skid-steering mobile robot.
Abstract:
This paper addresses the control of a team of nonholonomic mobile robots. Indeed, the most work, in this
domain, have studied extensively classical control for keeping a formation of mobile robots. In this work, the
leader mobile robot is controlled to follow an arbitrary reference path, and the follower mobile robot use the
sliding-mode controller to keep constant relative distance and constant angle to the leader robot. The efficiency
and simplicity of this control laws has been proved by simulation on different situations.
1 INTRODUCTION
The multi robots systems is an important robotics re-
search field. Such systems are of interest for many
reasons; tasks could be too complex for a simple robot
to accomplish; using several simple robots can be eas-
ier, cheaper and more flexible than a single power-
ful robot (Mazo et al., 2004), (Zavlanos and Pappas,
2008), (Murray, 2007), (Liu et al., 2007), (Klanˇcar
et al., 2009).
Formation control has been one of the important
research topics in multiple robot systems as it is appli-
cable to many areas such as geographical exploration,
rescue operations, surveillance, mine sweeping, and
transportation. Different approaches have been devel-
oped recently, for example, behavior-based control,
LQ control, visual servoing control, Lyapunov-based
control, input and output feedback linearization con-
trol, graph theory, and nonlinear control.
In leader-follower formation control, the most
widely used control technique is feedback lineariza-
tion based on the kinematics model of the system. In
this study, we focus on the problem of leader-follower
robot formation control using a sliding-mode con-
troller.
The referenced robot is called a leader, and the
robot following it called a follower. Thus, there are
many pairs of leaders and followers and complex for-
mations can be achieved by controlling relative posi-
tions of these pairs of robots respectively. This ap-
proach is characterized by simplicity, reliability and
no need for global knowledge and computation.
Figure 1: A skid-steered four wheel mobile robot.
In this paper, it will be developped a method based
on the leader-following approach to investigate for-
mation control problem in a group of nonholonomic
mobile robots. For this purpose, we design a new con-
troller based on sliding-mode control to drive a fleet
of mobile robots in a leader-follower configuration.
Sliding Mode Control (SMC) method has been
widely noticed because of its superior robust con-
trol performance for systems with highly uncertainty
(Chwa, 2004), (Yang and Kim, 1999), (Floquet et al.,
2003), (Solea and Nunes, 2007), (Solea and Cernega,
2009).
The rest of this paper is organized as follows. First
formulation of the nonholonomic mobile robot sys-
tem is revealed. Then, the leader-following formation
model method used by the robots is exposed. After
that, the architecture of the siling-mode controller is
described. This paper concludes with some simula-
tion and results.
161
Solea R., Cernega D., Filipescu A. and Serbencu A. (2010).
FORMATION CONTROL OF MULTI-ROBOTS VIA SLIDING-MODE TECHNIQUE.
In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 161-166
DOI: 10.5220/0002899501610166
Copyright
c
SciTePress

2 FORMATION CONTROL
2.1 Formulation of the Nonholonomic
Mobile Robot System
As indicated in Figure 1, the mobile robots are skid-
steering mobile platforms. To develop the kinematic
model for a skid-steering mobile robot (SSMR) that
is assumed to move in a plane (for simplicity) with an
inertial coordinate system, denoted by (X
g
, Y
g
), and
a local coordinate system, denoted by (X
r
, Y
r
), where
the origin of (X
r
, Y
r
) is fixed to the center of mass
(CG) of the SSMR as illustrated in Figure 2. The po-
sition and orientation of the CG, denoted by q(t) ∈ R
3
,
is defined as q = [x
r
y
r
θ
r
]
T
(i.e., the CG position, x
r
and y
r
, and the orientation θ
r
of the local coordinate
frame with respect to the inertial frame).
˙x
r
˙y
r
˙
θ
r
=
cos(θ
r
) −sin(θ
r
) 0
sin(θ
r
) cos(θ
r
) 0
0 0 1
·
v
xr
v
yr
ω
r
(1)
It is obvious that Eqn. (1) does not impose any
restrictions on the skid-steering mobile robot plane
movement, since it describes free-body kinematics
only. Therefore it is necessary to analyze the relation-
ship between wheel velocities and local velocities.
Suppose that the i − th wheel rotates with an an-
gular velocity ω
ir
(t), where i = 1, 2,...,4, which can
be seen as a control input. For simplicity, the thick-
ness of the wheel is neglected and is assumed to be
in contact with the plane at point P
ir
as illustrated in
Figure 3. In contrast to most wheeled vehicles, the lat-
eral velocity of the SMRR, v
iyr
, is generally nonzero.
This property comes from the mechanical structure of
the SSMR that makes lateral skidding necessary if the
vehicle changes its orientation. Therefore the wheels
are tangent to the path only if ω
r
= 0, i.e., when the
robot moves along a straight line.
Figure 2: Free body diagram.
Figure 3: Wheel velocities.
In this description we consider only a simplified
case of the SSMR movement for which the longitudi-
nal slip between the wheels and the surface can be ne-
glected. For traditional mobile robots, the wheel rota-
tion is translated into a linear motion along the tangent
of a curve without longitudinal slippage as described
by the following expressions:
v
ixr
= R
i
· ω
i
(2)
where v
ixr
is the longitudinal component of the total
velocity vector v
ir
of the i − th wheel expressed in
the local frame and R
i
denotes the so-called effective
rolling radius of that wheel.
The vectors d
i
(t) = [d
ix
(t),d
iy
(t)]
T
and d
CG
(t) =
[d
CGx
(t),d
CGy
(t)]
T
∈ R
2
are expressed in (X
r
,Y
r
) and
are defined from the instantaneous center of rotation
(ICR) of the vehicle to P
i
∀i = 1,2,...,4 and d
CG
(t)
from the ICR to the vehicle to CG, respectively, as il-
lustrated in Figure 3. Based on the geometry of Figure
3, the following expressions can be developed:
v
ixr
d
iy
=
v
xr
y
ICR
=
v
iyr
d
ix
= −
v
yr
x
ICR
= ω
r
(3)
where it is used the fact that the coordinates of the ICR
expressed in (X
r
,Y
r
), denoted by x
ICR
(t) and y
ICR
(t) ∈
R, are defined as [x
ICR
,y
ICR
]
T
= [−d
CGx
,d
CGy
]
T
.
From Figure 3 it is clear that the coordinates of
vectors d
ir
satisfy the following relationships:
d
1y
= d
4y
= d
CGy
− L
d
2y
= d
3y
= d
CGy
+ L
d
1x
= d
2x
= d
CGx
+ a
d
3x
= d
4x
= d
CGx
− b
(4)
After combining Eqns. (3) and (4), the follow-
ing relationships between wheel velocities can be ob-
tained:
v
L
= v
1xr
= v
4xr
v
R
= v
2xr
= v
3xr
v
F
= v
1yr
= v
2yr
v
B
= v
3yr
= v
4yr
(5)
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
162

where v
L
and v
R
denote the longitudinal coordinates
of the left and right wheel velocities, v
F
and v
B
are
the lateral coordinates of the velocities of the front
and rear wheels, respectively.
Using (3) - (5) it is possible to obtain the fol-
lowing transformation describing the relationship be-
tween the wheel velocities and the velocity of the
robot:
v
L
v
R
v
F
v
B
=
1 −L
1 L
0 −x
ICR
+ a
0 −x
ICR
− b
·
v
xr
ω
r
(6)
Notice that ω
L
and ω
R
which denote angular ve-
locities of left and right wheels, respectively, can be
regarded as control inputs at kinematic level and can
be used to control longitudinal and angular velocity
according to the following relationships:
v
xr
= R·
ω
R
+ ω
L
2
, ω
r
= R·
ω
R
− ω
L
2· L
(7)
while R is so called effective radius of wheels and 2·L
is a spacing wheel track depicted in Figure 2.
It is interesting to see that the analysed kinematic
model of the SSMR is quite similar to the kinematics
of the two-wheel mobile robot.
From the last equations it is clear that, theoreti-
cally, the pair of velocities ω
L
and ω
R
can be treated
as a control kinematic input signal as well as veloc-
ities v
xr
and ω
r
. However, the accuracy of the rela-
tions (7) mostly depends on the longitudinal slip and
can be valid only if this phenomenon is not dominant.
In addition, the parameters R and L may be identified
experimentally to ensure a high validity of the deter-
mination of the angular robot velocity with respect to
the angular velocities of the wheels.
To complete the kinematic model of the SSMR,
the following velocity constraint can be considered:
v
yr
+ x
ICR
· ω
r
= 0 (8)
The last equation is not integrable. In conse-
quence, it describes a nonholonomic constraint which
can be rewritten like:
−sin(θ
r
) cos(θ
r
) x
ICR
·
˙x
r
˙y
r
˙
θ
r
= 0 (9)
2.2 Leader-follower Formation Models
Figure 4 is a leader-follower control model where the
formation pattern is specified by the separate distance
d and the relative bearing ψ for two robots r1 and r2.
The desired formation pattern can be defined as the
desired separate distance d
d
and the relative bearing
Figure 4: Leader-follower approach for SSMR.
Figure 5: Block diagram.
ψ
d
. The follower r2 regulates the formation state er-
rors of the separate distance and the relative bearing
through its speed control signals u
r2
= [v
xr2
,ω
r2
]
T
:
˜
d
˜
ψ
=
d
d
ψ
d
−
d
ψ
(10)
The relative distance between the leader and the
follower robot is denoted as d, the separation bearing
angle is ψ, and they are given by:
d =
q
(x
r1
− x
c2
)
2
+ (y
r1
− y
c2
)
2
(11)
ψ = π − [θ
r1
− arctan2(y
r1
− y
c2
,x
r1
− x
c2
)] (12)
where:
x
c2
= x
r2
+ l · cos(θ
r2
), y
c2
= y
r2
+ l · sin(θ
r2
)
The formation control can be investigatedby mod-
eling the formation state error as follows (Das et al.,
FORMATION CONTROL OF MULTI-ROBOTS VIA SLIDING-MODE TECHNIQUE
163

2002):
˙
˜
d
˙
˜
ψ
= G· u
r2
+ F · u
r1
,
˙
φ = ω
r1
− ω
r2
(13)
and
G =
"
−cos(φ+ ψ) −l · sin(φ+ ψ)
sin(φ+ ψ)
d
−
l · cos(φ + ψ)
d
#
,
F =
"
cos(ψ) 0
−
sin(ψ)
d
1
#
where φ = θ
r1
− θ
r2
and l is the distance between the
robot position (x
r2
,y
r2
) and the robot hand position
(x
c2
,y
c2
) as shown in Figure 4.
2.3 Sliding-mode Controller Design
In a leader-follower configuration, with the leader’s
position given and once the follower’s relative dis-
tance and angle with respect to the leader are known,
the follower’s position can be determined. To use the
leader-following approach, it is assumed that the an-
gular and linear velocities of the leader are known.
In order to achieve and maintain the desired forma-
tion between the leader and follower, it is only need to
control the follower’s angular and linear velocities to
achieve the relative distance and angle between them
as specified. Therefore, the leader-following based
mobile robot formation control can be considered as
an extension of the tracking control problem of the
nonholonomic mobile robot.
A practical form of reaching the control law (pro-
posed by Gao and Hung (Gao and Hung, 1993)) is
defined as
˙s
i
= −p
i
· |s
i
|
α
· sgn(s
i
), 0 < α < 1, i = 1,2 (14)
This reaching law increases the reaching speed
when the state is far away from the switching man-
ifold, but reduces the rate when the state is near the
manifold. The result is a fast reaching and low chat-
tering reaching mode.
A new design of sliding surface is proposed, such
that the separation bearing angle, ψ and the orienta-
tion error φ, are internally coupled with each other in
a sliding surface leading to convergence of both vari-
ables. For that purpose the following sliding surfaces
is proposed:
s
1
=
˙
˜
d + γ
d
·
˜
d (15)
s
2
=
˙
˜
ψ+ γ
ψ
·
˜
ψ+ γ
0
· sgn(
˜
ψ) · | φ| (16)
here γ
0
, γ
d
, γ
ψ
are positive constant parameters and
˜
d,
˜
ψ, φ are defined by (10), (13).
−4 −2 0 2 4 6
−2
0
2
4
6
8
10
Trajectory
x [m]
y[m]
leader
follower
Figure 6: Simulation I - Trajectory of the leader and the
follower.
If s
1
converges to zero, trivially
˜
d converges to
zero. If s
2
converges to zero, in steady-state it be-
comes
˙
˜
ψ = −γ
ψ
·
˜
ψ− γ
0
· sgn(
˜
ψ) · |φ|. Since |φ| is al-
ways bounded, the following relationship between
˜
ψ
and
˙
˜
ψ holds:
˜
ψ < 0 ⇒
˙
˜
ψ > 0 and
˜
ψ > 0 ⇒
˙
˜
ψ < 0.
From the time derivative of (15) and (16) and us-
ing the reaching law defined in (14) yields:
˙s
1
=
¨
˜
d + γ
d
·
˙
˜
d = −p
1
· |s
1
|
α
· sgn(s
1
) (17)
˙s
2
=
¨
˜
ψ+ γ
ψ
·
˙
˜
ψ+ γ
0
· sgn(
˜
ψ) · sgn(
˜
φ) ·
˙
φ =
= −p
2
· |s
2
|
α
· sgn(s
2
)
(18)
After some mathematical manipulation, one can
achieve:
˙v
xc2
=
p
1
· |s
1
|
α
· sgn(s
1
) + γ
d
·
˙
˜
d − D
1
cos(φ+ ψ)
(19)
˙
ω
c2
=
(p
2
· |s
2
|
α
· sgn(s
2
) + γ
psi
·
˙
˜
ψ) · d − D
2
l · cos(φ+ ψ)
(20)
where
D
1
= l ·
˙
ω
r2
· sin(φ + ψ) − d· (
˙
φ+
˙
ψ) · (
˙
ψ+ ω
r1
)−
− ˙v
xr1
· cos(ψ) − v
xr1
·
˙
φ· sin(ψ)
D
2
= γ
0
· sgn(
˜
ψ· φ) ·
˙
φ· d − ˙v
xr2
· sin(φ + ψ)+
+ ˙v
rx1
· sin(ψ) − v
xr1
·
˙
φ· cos(ψ) − (
˙
φ+
˙
ψ) ·
˙
d−
−d ·
˙
ω
r1
−
˙
d · (
˙
ψ+ ω
r1
)
The signum functions in the sliding surface were
replaced by saturation functions, to reduce the chat-
tering phenomenon (Slotine and Li, 1991).
3 SIMULATION RESULTS
In this section, simulation results for the proposed
SMC are presented. The simulation are performed
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
164

in Matlab/Simulink environment to verify behavior of
the controlled system. The parameters of the SSMR
model were chosen to correspond as closely as possi-
ble to the real experimental robot presented in section
1 in the following manner: a = 0.10[m], b = 0.20[m],
L = 0.12[m], R = 0.04[m]. Wheel velocity commands,
0 10 20 30 40 50 60
−0.4
−0.2
0
0.2
0.4
Sliding surfaces s
1
and s
2
time [s]
s
1
, s
2
s
1
s
2
(a)
0 10 20 30 40 50 60
−0.2
−0.1
0
0.1
0.2
0.3
0.4
0.5
0.6
Separate distance
time [s]
d tilde [m]
(b)
0 10 20 30 40 50 60
−50
−40
−30
−20
−10
0
10
Relative bearing (ψ tilde) and relative orientation (φ)
time [s]
ψ tilde, φ [deg]
ψ tilde
φ
(c)
Figure 7: Simulation I - Sliding surfaces s
1
and s
2
, separate
distance (
˜
d), relative bearing (
˜
ψ) and relative orientation
(φ).
ω
R
=
v
xc2
+ L· ω
c2
R
; ω
L
=
v
xc2
− L· ω
c2
R
; (21)
are sent to the power modules of the follower mobile
robot, and encoder measures NR and NL are received
−2 0 2 4 6 8 10
−2
0
2
4
6
8
10
Trajectory
x [m]
y[m]
leader
follower
Figure 8: Simulation II - Trajectory of the leader and the
follower.
in the robots pose estimator for odometric computa-
tions.
Figure 5 shows a block diagram of the proposed
sliding-mode controller.
In order to compute the actuating control input,
equation (6) needs to be integrated and some initial
values v
xc2
(0), ω
c2
(0) to be fixed.
Two simulation experiments were carried out to
evaluate the performance of the sliding mode con-
troller presented in Section 2.3. The first simula-
tion refers to the case of circular trajectory (v
xr1
=
0.4[m/s] and ω
r1
= 0.1[rad/s]). The initial condi-
tions of the leader and the follower are, x
r1
(0) =
0.5, y
r1
(0) = 0, θ
r1
(0) = 0, x
r2
(0) = 0, y
r2
(0) = 0,
θ
r1
(0) = 0, d
d
= 1.0[m], ψ
d
= 135[deg].
In the second simulation the leader robot execute a
linear trajectory but with a non-zero initial orietation
(θ
r1
= 45[deg]). The initial conditions of the leader
and the follower in this second case are, x
r1
(0) = 0.5,
y
r1
(0) = 0, θ
r1
(0) = pi/4, x
r2
(0) = 0, y
r2
(0) = 0,
θ
r1
(0) = 0, d
d
= 1.0[m], ψ
d
= −120[deg].
Figure 6 shows the trajectory of the leader and the
follower for the first simulation case. In order to have
a temporal reference in the figure the robots are drawn
each second: the blue car represent the leader and the
red car represent the follower.
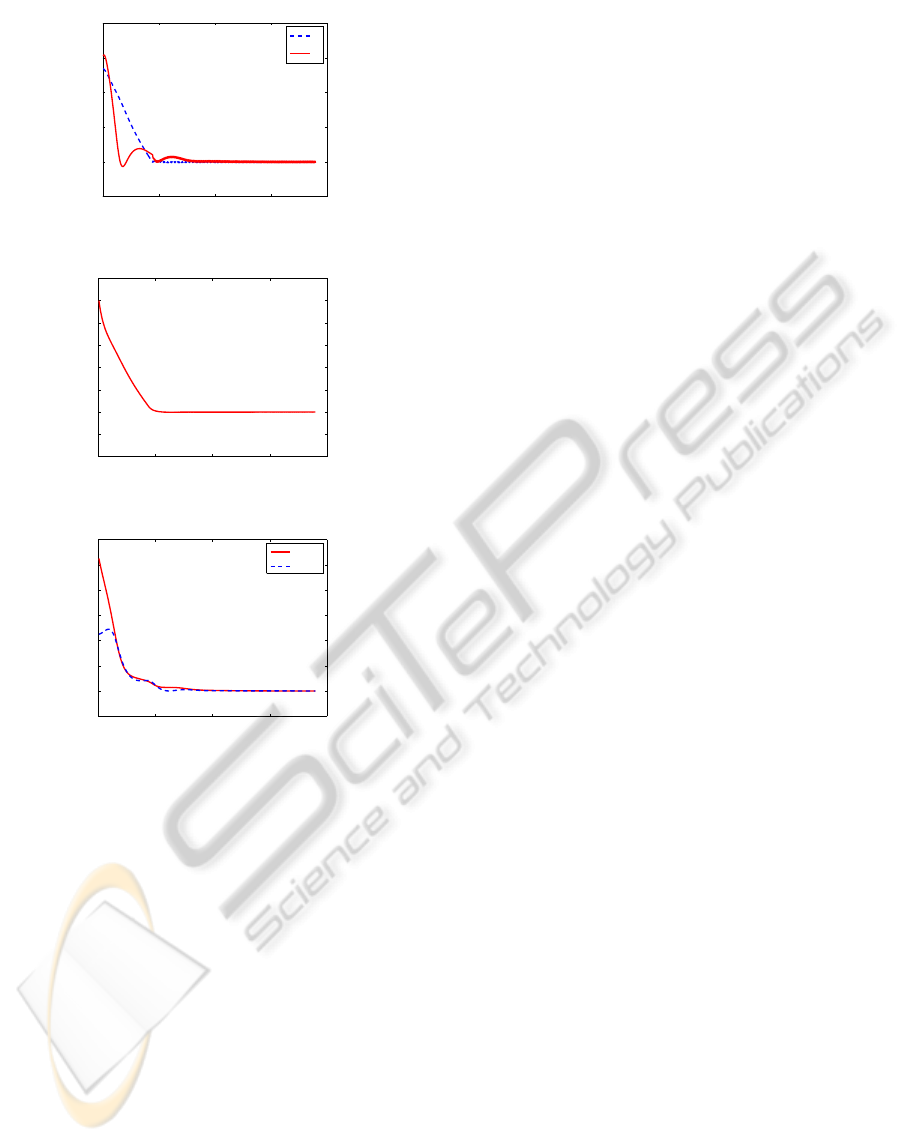
In Figure 7.a the sliding surfaces s
1
and s
2
asymp-
totically converge to zero. Finally, Figures 7.b and c
show the time histories of
˜
d,
˜
ψ and φ.
The results of the second case called Simulation
II are given in Figures 8 - 9. Figure 8 shows the tra-
jectory of the leader and the follower, Figures 9 the
sliding surfaces and the time histories of
˜
d,
˜
ψ and φ.
The good performance for controlling the forma-
tion with the developed control law can be observed
from Figures 6 - 9. The outputs of the formation sys-
tem (
˜
d,
˜
ψ and φ) asymptotically converge to zero, as
shown in Figures 7 and 9.
FORMATION CONTROL OF MULTI-ROBOTS VIA SLIDING-MODE TECHNIQUE
165
0 10 20 30 40
−0.2
0
0.2
0.4
0.6
0.8
Sliding surfaces s
1
and s
2
time [s]
s
1
, s
2
s
1
s
2
(a)
0 10 20 30 40
−0.2
−0.1
0
0.1
0.2
0.3
0.4
0.5
0.6
Separate distance
time [s]
d tilde [m]
(b)
0 10 20 30 40
−20
0
20
40
60
80
100
120
Relative bearing (ψ tilde) and relative orientation (φ)
time [s]
ψ tilde, φ [deg]
ψ tilde
φ
(c)
Figure 9: Simulation II - Sliding surfaces s
1
and s
2
, separate
distance (
˜
d), relative bearing (
˜
ψ) and relative orientation
(φ).
4 CONCLUSIONS
In this paper is proposed a sliding mode forma-
tion tracking control scheme of nonholonomic mobile
robots. The leader and follower are a skid-steering
mobile robots. The desired formation, defined by two
parameters (a distance and an orientation function) is
allowed to vary in time. The effectiveness of the pro-
posed designs has been validated via simulation ex-
periments.
Future research lines includethe experimental val-
idation of our control scheme and the extension of our
results to skid-steering mobile robots. For the sake of
simplicity in the present paper a single-leader, single-
follower formation has been considered. Future in-
vestigations will cover the more general case of multi-
leader, multi-follower formations.
ACKNOWLEDGEMENTS
This work was supported by CNCSIS-UEFISCSU,
projects PNII-IDEI 506/2008 and PNII-IDEI
641/2007.
REFERENCES
Chwa, D. (2004). Sliding-mode tracking control of non-
holonomic wheeled mobile robots in polar coordi-
nates. IEEE Transactions on Control, 12(4):637–644.
Das, A., Fierro, R., Kumar, V., Ostrowski, J., Spletzer, J.,
and Taylor, C. (2002). A vision-based formation con-
trol framework. IEEE Transactions on Robotics and
Automation, 18(5):813–825.
Floquet, T., Barbot, J. P., and Perruquetti, W. (2003).
Higher-order sliding mode stabilization for a class
of nonholonomic perturbed systems. Automatica,
39(6):1077–1083.
Gao, W. and Hung, J. C. (1993). Variable structure control
of nonlinear systems: A new approach. IEEE Trans-
actions on Industrial Electronics, 40(1):45–55.
Klanˇcar, G., Matko, D., and Blaˇziˇc, S. (2009). Wheeled
mobile robots control in a linear platoon. Journal of
Intelligent and Robotic Systems, 54(5):709–731.
Liu, S.-C., Tan, D.-L., and Liu, G.-J. (2007). Robust leader-
follower formation control of mobile robots based on
a second order kinematics model. Acta Automatica
Sinica, 33(9):947–955.
Mazo, M., Speranzon, A., Johansson, K., and Hu, X.
(2004). Multi-robot tracking of a moving object us-
ing directional sensors. In IEEE International Con-
ference on Robotics and Automation, ICRA ’04, vol-
ume 2, pages 1103–1108.
Murray, R. M. (2007). Recent research in cooperative con-
trol of multi-vehicle systems. Journal of Dynamic Sys-
tems, Measurement, and Control, 129(5):571–583.
Slotine, J. J. E. and Li, W. (1991). Applied Nonlinear Con-
trol. Prentice-Hall.
Solea, R. and Cernega, D. (2009). Sliding mode control for
trajectory tracking problem - performance evaluation.
In Lecture Notes in Computer Science, Springer, vol-
ume 5769, pages 865–874.
Solea, R. and Nunes, U. (2007). Trajectory planning and
sliding-mode control based trajectory-tracking for cy-
bercars. Aided Engineering, IOS Press, 14(1):33–47.
Yang, J.-M. and Kim, J.-H. (1999). Sliding mode control
for trajectory tracking of nonholonomic wheeled mo-
bile robots. IEEE Transactions on Robotics and Au-
tomation, 15(3):578–587.
Zavlanos, M. M. and Pappas, G. J. (2008). Dynamic assign-
ment in distributed motion planning with local coor-
dination. IEEE Transactions on Robotics, 24(1):232–
242.
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
166
