MODELING TIME CONSTRAINTS

IN INTER-ORGANIZATIONAL WORKFLOWS

Mouna Makni

1,3

, Nejib Ben Hadj-Alouane

, Moez Yeddes

and Samir Tata

National Engineering School of Tunis, OASIS Laboratory, Tunis, Tunisia

National School of Computer Sciences, CRISTAL Laboratory, Tunis, Tunisia

Institut TELECOM, TELECOM SudParis, UMR CNRS Samovar,

Evry, France

Keywords:

Inter-organizational, Workﬂows, Time constraints, Time Petri nets, Models.

Abstract:

This paper deals with the integration of temporal constraints within the context of Inter-Organizational Work-

ﬂows (IOWs). Obviously, expressing and satisfying time deadlines is important for modern business processes,

and need to be optimized for efﬁciency and extreme competitiveness. In this paper, we propose a temporal

extension to CoopFlow (Tata et al., 2008), an existing approach for designing and modeling IOWs, based

on Time Petri Net models and tools. Methods are given, based on reachability analysis and model checking

techniques, for verifying whether or not the added temporal requirements are satisﬁed, while maintaining the

core advantage of CoopFlow; i.e. that each partner can keep the critical parts of its business process private.

1 INTRODUCTION

In recent years, companies have proven that collab-

oration plays a very signiﬁcant role in facing indus-

trial competition and pressures. In this new modern

environment, it is important for business partners to

rapidly join forces in order to create new and valuable

expertise, with cheaper costs and within restrictive

deadlines. For this purpose, companies have largely

adopted workﬂow concepts and techniques. In order

to promote a virtual environment within which com-

panies can effectively engage each other, two impor-

tant processes need to be properly designed: (1) work-

ﬂow abstraction, and (2) workﬂow matching (Tata

et al., 2008).

In fact, the basic supposition of a proper virtual

environment is that the description of the business

processes of the partners are well advertised and read-

ily available in a common registry. A challenging

issue is industrial secret preservation (Amirreza and

Eder, 2008; Chebbi et al., 2006), especially in oc-

casional collaboration where there are serious conse-

quences for companies with regards to fully exposing

their business knowledge. Thus, abstraction is a ﬁrst

step used prior to advertising, and consists of elimi-

nating details that are not necessary for cooperation

needs. The next step is matching, which consists of

identifying and selecting the appropriate partner able

to provide the required service. Within the above con-

text, the CoopFlow approach is designed to sup-

port short-term ascending workﬂow cooperation

within virtual enterprises, using the publish/subscribe

paradigm. We have already presented the basic ideas

of the CoopFlow approach and compared it with the

existing approaches for workﬂows cooperation (Tata

et al., 2008).

So far, in CoopFlow, the focus has been on the

structural conformance of the processes of the part-

ners; i.e., the partners which execute complementary

tasks can interconnect within an Inter-Organizational

Workﬂow (IOW). In this paper, we undertake the new

concern of ensuring that the timing constraints and/or

expectations of the involved partners are also compat-

ible. With regards to functional requirements, work-

ﬂow behaviors are typically closely tied to the timing

requirements. Therefore, enterprises, which are gen-

erally looking for cost reduction, should strive to in-

clude timing requirements as part of their workﬂow

matching process.

Our main purpose in this paper is to provide a

time-oriented inter-organizational workﬂow model-

ing and management framework, within the context

of CoopFlow. Such a framework will enable enter-

prises to specify temporal constraints and detect, early

on, temporal contradictions that may constitute ob-

stacles for their cooperation. For instance, deadlines

constraints can be violated if all participating enter-

prises do not respect their allowed temporal bounds

221

Makni M., Ben Hadj-Alouane N., Yeddes M. and Tata S. (2010).

MODELING TIME CONSTRAINTS IN INTER-ORGANIZATIONAL WORKFLOWS.

In Proceedings of the 12th International Conference on Enterprise Information Systems - Information Systems Analysis and Speciﬁcation, pages

221-229

DOI: 10.5220/0002902202210229

 SciTePress

for delivering the invoked services. Given an ab-

stracted version of its business process, a company

should add temporal expectations for actions that will

be performed by external parties i.e. time duration af-

ter which the supplied services cannot be performed

anymore. On the other side, eventual partners will

be able to capture temporal requirements as well as

business behavior from the common registry, in order

to execute temporal reasoning and veriﬁcation. Thus,

they can detect whether deadlines constraints will be

satisﬁed or violated in the resulting IOW.

This paper is organized as follows. Section 2

presents the necessary background from Time Petri

Nets, needed to understand our work. Section 3

presents an overview of the existing CoopFlow ap-

proach to illustrate our needs. Section 4 exposes our

method, based on Time Petri Nets, for incorporating

timed constraints. Section 5 presents a survey of the

important articles in the literature related to this pa-

per’s topic, and dealing essentially with timed models

for workﬂow.

2 BACKGROUND

In this section we present some preliminaries and def-

initions that are useful for our work. CoopFlow uses

the Petri Net (PN) formalism to have powerful work-

ﬂow analysis and validation techniques. In order to

introduce time constraints, we adopt Time Petri Nets

(TPN), which is one of Petri Nets time extensions pro-

posed by Merlin (Merlin, 1974). As workfow systems

are generally ﬁnite, they can be modeled by bounded

Time Petri Nets, which offers a useful tool for work-

ﬂow temporal behavior analysis.

Deﬁnition 1: Time Petri Nets. A TPN

(Berthomieu and Diaz, 1991) is a tuple

(P,T,B,F, M

,S) where:

• P is a ﬁnite set of places;

• T is a ﬁnite set of transitions;

• B : T ×P → N is the backward incidence function;

• F : T × P → N is the forward incidence function;

• M

: P → N is the initial marking function, and,

• S : T → Q

× (Q

∪∞) is a mapping called static

interval.

Assuming that θ is the instant a transition t be-

comes enabled for the last time and S(t) = [a, b] is

the interval associated, then [θ + a, θ + b] is the time

range to ﬁre the transition, except if t is disabled by

ﬁring another conﬂicting transition. A clock is as-

sociated to each validated transition to count elapsed

time until its ﬁring date. a and b are called the ear-

lier (EFT) and last (LFT) ﬁring times. Firing a tran-

sition is instantaneous and modiﬁes the marking as

classical Petri Nets. Moreover, some variations can

be found in the literature concerning transition ﬁr-

ing (Berthomieu and Diaz, 1991; Pezze and Young,

1999). We consider the Strong Time Semantics (STS)

semantic, where an enabled transition must be ﬁred

at least when time reaches the LFT limit, unless it

is disabled by another transition ﬁring. In this case,

temporal constraints are sufﬁcient to resolve conﬂicts

between transitions.

Deﬁnition 2: State Classes Graph. A state of the

TPN can be deﬁned by a couple (M,I) where:

• M is a net marking, and,

• I is a vector of intervals corresponding to ﬁring

intervals for each transition enabled by M.

Obviously, we can see that reachable states from

the initial marking is inﬁnite because, in part, pos-

sible ﬁring times for each transition are inﬁnite. To

analyze TPN behavior and state reachability, an enu-

merative technique is proposed in (Berthomieu and

Menasche, 1983) based on state classes. This tech-

nique leads to a state class graph (SCG) generation

which is an oriented graph that represents all possi-

ble sequences of ﬁring values during each transition

ﬁrings times. SCG generation is automated using the

tool TINA (Berthomieu and Vernadat, 2006). Then,

some properties such as accessibility, marking and

temporal bounds can be checked on the graph.

3 THE CoopFlow APPROACH

In the context of short-term cooperation, enterprises

with complementary skills are dynamically intercon-

nected according to their needs. Our work consists

of an extension of CoopFlow (Tata et al., 2008), a

bottom-upapproach that allows dynamic interconnec-

tion of a set of partners by providing a useful arti-

fact for their privacy preservation. CoopFlow consists

of three steps: (1) workﬂow abstraction and adver-

tisement, (2) workﬂow matching and interconnection,

and (3) workﬂow cooperation.

The goal of the ﬁrst step is to allow partners to

publish their business processes in a common registry

without revealing their workﬂow’s internal structures.

This is done by the abstraction process and the re-

sulting public workﬂow exposes only cooperative ac-

tivities required for cooperation needs. The match-

ing process in the second step consists of comparing

ICEIS 2010 - 12th International Conference on Enterprise Information Systems

222

the business behavior of the candidates i.e. of pub-

lic workﬂows published in the registry, according to

a given criteria. If the result is positive, workﬂows

are then interconnected. We have used Petri Nets

and symbolic observation graphs as theoretical foun-

dations for workﬂow abstraction and matching (Klai

et al., 2009; Chebbi and Tata, 2007). The third and

last step consists of the inter-enterprises workﬂow co-

operation platform (deployment, execution, manage-

ment, etc...) (Chebbi and Tata, 2005).

We present a running example which will detail

the abstraction and the matching processes.

OrderProd

p11

p13

p14

p16

p17

p15

End

p12

OrderP2

StockP1

ShipP2

AsmblP1P2

RelProd

p18

p19

PayP2

BillP2

(a) (Partner1)

OrderP2

p21

p24

End

p26

p27

p25

p23

Init1

RelStock

p22

PlanProd

Init2

Init3

Prod

Order

ShipP2

p29

p28

PayP2

BillP2

(b) (Partner2)

Figure 1: The client/provider example.

3.1 Running Example

Lets us consider a client/provider example in an in-

dustrial context, involving two candidates for a work-

ﬂow cooperation: Partner1 and Partner2. Partner1

business process, shown in ﬁgure 1(a), supplies an in-

dustrial product, made up of two components P1 and

P2. The product processing is launched when the cor-

responding order is received (OrderProd). While P1

is available in the stock, P2 should be requested to

an external supplier (OrderP2). When the two com-

ponents are available (StockP1 and ShipP2), they are

assembled (AsmblP1P2) and the product is delivered

to the client (RelProd). Finally, Partner1 receives the

bill (BillP2) and makes the payment (PayP2).

On the other hand, the Partner2’s workﬂow is il-

lustrated in ﬁgure 1(b). After receiving an order to de-

liver component P2 (OrderP2), and as a result of cus-

tomer speciﬁcations analysis (PlanProd), three cases

are possible. Partner2 can either recover the order

in the stock (RelStock), produce P2 locally (Prod),

or supply it to a third participant (Order). When

component P2 is built, it is shipped to the customer

(ShipP2). Then, the bill is sent to Partner1 (BillP2),

for the payment reception (PayP2). Filled transitions

represent the cooperative activities, while others are

internal activities and are not supposed to be visible

to other partners.

3.2 The Abstraction Process

To support cooperation, one has to deal with the part-

ners’ privacy respect. In (Chebbi and Tata, 2007), we

proposed a set of reduction rules as well as an ab-

straction algorithm. Given an initial workﬂow, the

principle of the algorithm consists in removing all in-

ternal activities whose elimination doesn’t affect the

visible behavior of the initial workﬂows. Thus, we

start by identifying the various reduction patterns and

then applying them the suitable reduction rules. This

procedureis repeated until the removingof all internal

activities that don’t play any direct role in the coop-

eration. The abstraction process applied to the private

workﬂows of Partner1 and Partner2, generates the

public workﬂows illustrated in Figure 2.

p12

p13

p11

OrderP2

ShipP2

End

p14

PayP2

BillP2

(a) (Partner1)

p22

p23

p21

OrderP2

ShipP2

End

p24

PayP2

BillP2

(b) (Partner2)

Figure 2: The public workﬂow of the partners.

3.3 The Matching Process

Given public workﬂows advertised in a registry, the

selection criteria making a choice of an effective part-

ner is based on the observable behavior, i.e. the

behavior on the cooperative transitions, which must

match with the observable behavior of the eventual

partner. Two cooperative transitions are considered

equivalent according to their business semantics if

they are described using references to equivalent con-

cepts in a semantic model. If the matching result is

positive, the workﬂows are then interconnected. In

the example above, we notice the business behav-

ior complementary of Partner1 and Partner2 work-

ﬂows. As shown in Figure 3, interconnection can be

MODELING TIME CONSTRAINTS IN INTER-ORGANIZATIONAL WORKFLOWS

223

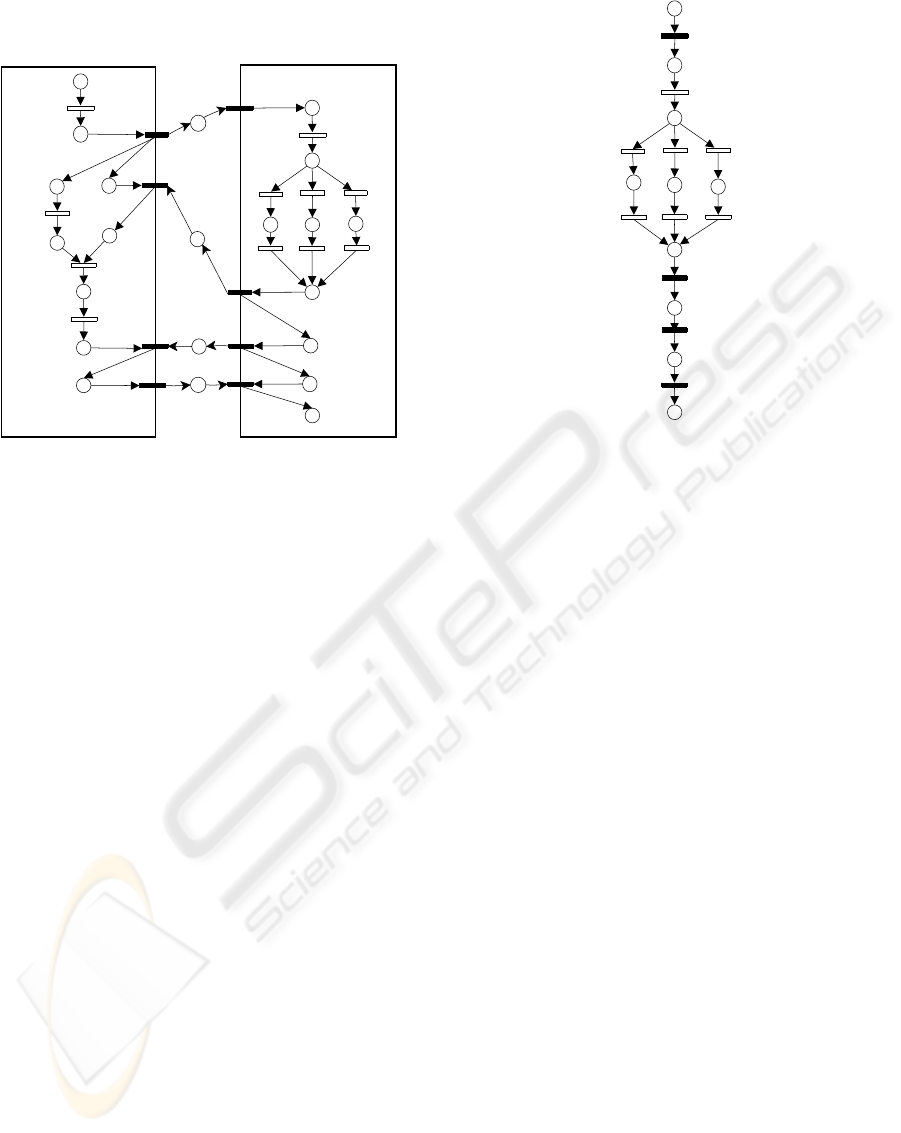
held between the corresponding transitions OrderP2,

ShipP2, BillP2 and PayP2 of Partner1 and Partner2.

OrderProd

p11

p13

p14

p16

p17

p15

p12

OrderP2

StockP1

AsmblP1P2

RelProd

p18

p19

PayP2

BillP2

OrderP2

p24

End

p26

p27

p25

p23

Init1

StockP2

p22

PlanProd

Init2

Init3

ProdP2

Order

ShipP2

p29

p28

PayP2

BillP2

ShipP2

Figure 3: The inter-organizational workﬂow.

3.4 Dealing with Time Constraints

In the context of cooperation, partners generally want

to run a workﬂow within a speciﬁc period of time.

In the previous example, it is obvious that Partner1

needs information concerning P2 delivery due date,

because the cooperation can be achieved only if P2

delivery is properly attended on time. We propose

to use the TPN formalism for modeling temporal

behavior of the given workﬂows. Figure 4 illus-

trates the temporal version of the internal workﬂow

of Partner2. We can see that the necessary duration

for P2 delivery depends on the case executed:

• if P2 is available on the stock, the processing takes

at least 2 time units, at most 4 times units;

• if P2 is produced by Partner2, the processing

takes at least 4 time units, at most 6 times units,

and,

• if P2 is supplied to an external provider, the pro-

cessing takes at least 5 time units, at most 7 times

units.

Let us consider a situation in which Partner1 speci-

ﬁes that P2 delivery should not exceed 3 time units

since the order is sent. Partner2 is able to satisfy

Partner1’s constraint only if P2 is available on the

stock. Thus, even if the structural conformance of

the candidates is validated by the matching process,

their corresponding public workﬂows do not contain

enough information to ensure that timing constraints

of the involved partners are also compatible. Spec-

ifying deadlines becomes a base requirement within

OrderP2

p21

p24

p26

p27

p25

p23

Init1

RelStock

p22

PlanProd

Init2

Init3

Prod

Order

ShipP2

[0,1]

[1,1]

[0,0]

[0,1]

[2,3]

[3,4]

[1,1]

End

p29

PayP2

BillP2

[0,1]

[0,3]

p28

Figure 4: The temporal private workﬂow of Partner2.

IOWs, especially in a critical business context (ﬁnan-

cial, medical, etc.), where some parties want to pay

more but also imposes stricter services delivery times.

If the deadline is violated, they can ask for compen-

sation. Thus, some temporal information have to be

added as part of to the advertised public workﬂows in

order to allow eventual partners to verify that dead-

lines are respected, which will lead to a successful

execution of the resulting IOW.

4 TEMPORAL CONSTRAINTS IN

COOPFLOW

4.1 Our Approach

As explained above, according to CoopFlow ap-

proach, each partner holds locally a Petri Net model-

ing its business process. The abstraction process gen-

erates the corresponding public process which will be

published in the common registry. In order to provide

a CoopFlow temporal extension, we assume that:

• each partner, given its business process modeled

by a PN, also holds a timed version modeled by a

TPN, called ”Private temporal workﬂow”, and,

• given time intervals associated with activities, a

partner is able to specify the estimated execution

times of its critical supplied tasks. These deadline

constraints are called ”Timing constraints”.

We propose in this section a method for model-

ing deadlines between critical cooperative activities.

ICEIS 2010 - 12th International Conference on Enterprise Information Systems

224

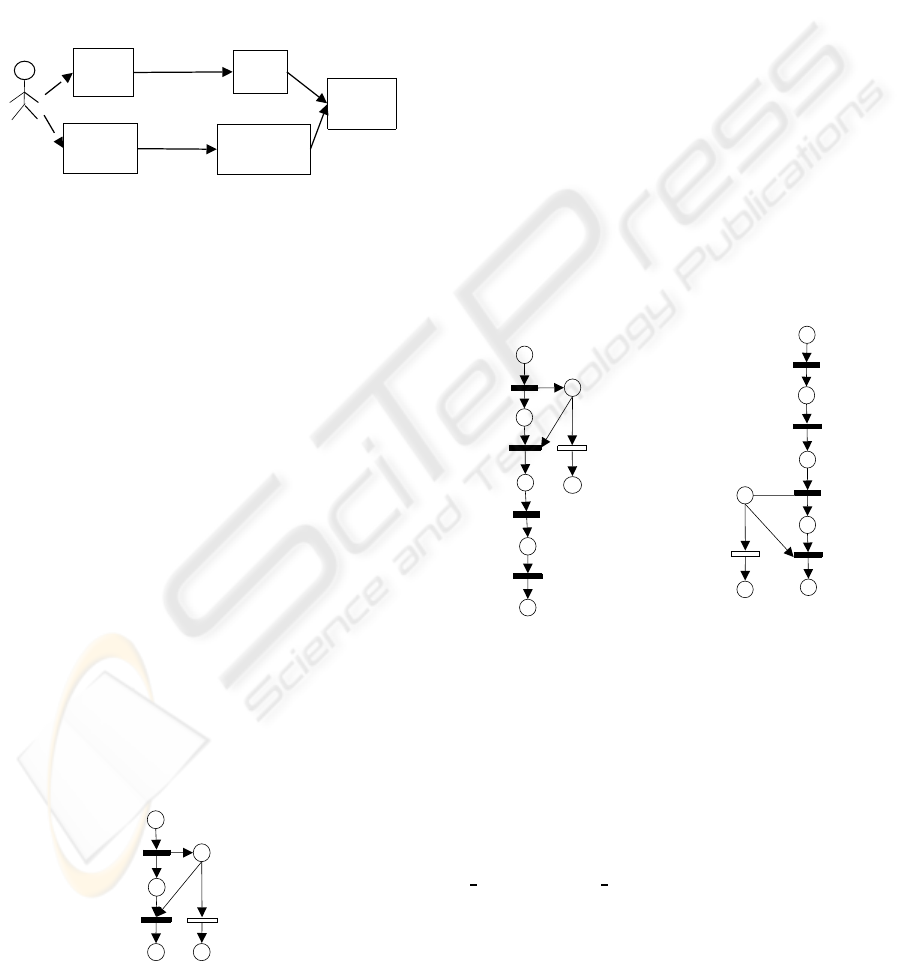
Our approach, illustrated in Figure 5, is based on the

existence of a public workﬂow generated following

the abstraction process. It consists of adding to this

abstract representation deadline constraints between

two cooperative activities, interacting with the same

company, and referring to a duration limit between an

input and an output messages. Several deadlines can

be speciﬁed by a partner. Attached constraints will be

advertised in the common registry and propagated to

external parties as part of the resulting ”Public tem-

poral workﬂow”.

Partner

Private

Internal

plan

calculation

Timing

constraints

Private

temporal

Abstraction

process

Public

temporal

Figure 5: A CoopFlow timed extension.

Even if the internal business process is not chang-

ing, the deadlines speciﬁed by a partner may vary and

can be dynamically managed while computing the es-

timated execution times. Thus, depending on its inter-

nal plan execution and its available resources, a part-

ner is able to advertise several ”Public temporal work-

ﬂow” versions, in order achieve different cooperation

needs, depending on clients requirements.

4.2 Modeling Deadline Constraints

While TPN absolute time informationis not preserved

through local clocks in TPN, a simple alternative, in-

troduced by (Toussaint et al., 1997), consists of mod-

eling a parameter in the corresponding TPN which

describes the allowed execution time between two

events. The parameter includes a set of places and

transitions representing a non-intrusive observer, and

transforms the problem into a reachability analysis of

a speciﬁc state. This approach, detailed in (Godary,

2008), is illustrated in ﬁgure 6, in which an observer

is introduced to supervise the maximum duration be-

tween transitions Begin and End.

Begin

End

MaxDuration

ERROR

Observer

[10,10]

[0,0]

[4,9]

Figure 6: A deadline constraint modeled by an observer.

When the transition MaxDuration is validated (by

the existence of a token in the place Observer), the

associated clock is enabled. The token will be used

either by ﬁring transition End if the constraint is satis-

ﬁed or transition MaxDuration if the given time limit

is reached. Checking the maximum duration becomes

an analysis of the reachability of place ERROR, which

is marked if the execution time is longer than the spec-

iﬁed duration.

4.3 Incorporating Timing Constraints

and Advertisement

Let us consider the following constraints for the pre-

vious example:

• between the instant Partner1 orders for compo-

nent P2 (OrderP2) and the time a reception noti-

ﬁcation is received (ShipP2), he waits at most 3

time units;

• between the instant Partner2 sends the bill for P2

delivery (BillP2) and the instant the payment is

received (PayP2), he waits at most 10 time units.

p12

p13

p11

OrderP2

ShipP2

End

p14

PayP2

BillP2

C_Partner1

ERROR

Observer

[3,3]

[0,0]

(a) (Partner1)

p22

p23

p21

OrderP2

ShipP2

End

p24

PayP2

BillP2

C_Partner2

ERROR

Observer

[10,10]

[0,0]

(b) (Partner2)

Figure 7: The public temporal workﬂow of the partners.

To advertise these properties, partners would have

to translate these informal requirements into the tem-

poral constraint model. Figure 7 illustrates such an

advertisement for the two previous constraints: an ob-

server is added in the corresponding public workﬂow

between the critical cooperative transitions, showing

the constraint as the associated temporal interval to

C Partner1 and C Partner2 transitions.

MODELING TIME CONSTRAINTS IN INTER-ORGANIZATIONAL WORKFLOWS

225

4.4 Workﬂow Matching and

Interconnection

Public temporal workﬂows contain enough informa-

tion to ensure the structural and temporal suitability

of the eventual partners. First, the business comple-

mentarity behavior is validated by the algorithms de-

ﬁned in CoopFlow. If this ﬁrst step is successful, an

analysis is done to validatethe temporal behavior con-

formance of the eventual partners as follows.

4.4.1 Reproducing Temporal Constraints into

Private Temporal Workﬂows

When a partner receives a time constraints advertise-

ment, he should execute locally a temporal reasoning

and veriﬁcation to validate that the deadline will be

satisﬁed in the IOW. This means that a partial IOW

is generated using its private temporal workﬂow and

the received public temporal workﬂow which includes

the observer. The deadline respect is equivalent to the

analysis of the reachability of place ERROR. Fig-

ure 8 and 9 illustrate private temporal workﬂows of

Partner1 and Partner2, combined with the corre-

sponding public temporal workﬂows advertised.

OrderProd

p11

p13

p14

p16

p17

p15

p12

OrderP2

StockP1

AsmblP1P2

RelProd

p18

p19

PayP2

BillP2

OrderP2

End

p21

ShipP2

p22

PayP2

BillP2

ShipP2

p01

p02

p03

p04

C_Partner2

ERROR

Observer

[10,10]

p23

[0,1]

[1,1]

[0,1]

[1,1]

[0,1]

[2,5]

[0,0]

Figure 8: The timed workﬂow veriﬁcation for Partner1.

4.4.2 Timed Veriﬁcation

Introducing an observer transforms the problem into

a reachability analysis of place ERROR. This can be

done using the tool TINA (Berthomieu and Vernadat,

2006), which automatically generates the state classes

graph. Three cases can be found:

p11

p01

p12

p13

OrderP2

p14

PayP2

BillP2

OrderP2

p23

End

p25

p26

p24

p22

Init1

StockP2

p21

PlanProd

Init2

Init3

ProdP2

Order

ShipP2

p28

p27

PayP2

BillP2

ShipP2

p02

p03

p04

C_Partner1

ERROR

Observer

[3,3]

[0,0]

[0,1]

[1,1]

[0,0]

[0,1]

[2,3]

[3,4]

[1,1]

[0,1]

[0,3]

Figure 9: The timed workﬂow veriﬁcation for Partner2.

• a state including the place ERROR in its marking

is never reachable, while the place End is acces-

sible; this means that all the ﬁring sequences and

times verify the required deadline;

• the place ERROR is reachable but the place End is

never accessible; this means that the desired prop-

erty is never satisﬁed;

• the two speciﬁc places ERROR and End appear in

the corresponding state classes graph; this means

that the deadline constraint is not always satisﬁed.

We need a further investigation to detect restric-

tions to apply allowing the partner to satisfy dead-

line constraint.

A preliminary veriﬁcation leads to the identiﬁcation

of the two cases in which the cooperation can always

or can not be positive. Following this result, and if the

matching is positif, cooperation move to the next step

which is workﬂow interconnection.

• Timed Veriﬁcation for Partner1. Let us consider

reachable state classes, generated by TINA, for

the partial Inter-OW illustrated in ﬁgure 8. The in-

terval associated to the transitionC Partner2 is 10

time units. Table 1 shows that the place ERROR is

never reachable (i.e. C Partner2 is a dead transi-

tion). This means that, while the reachable states

are inﬁnite because of the temporal interval asso-

ciated to each transition, the deadline constraint is

always respected.

• Timed Veriﬁcation for Partner2. Partner2

should also verify the temporal constraint adver-

ICEIS 2010 - 12th International Conference on Enterprise Information Systems

226

Table 1: The Partner1 state classes for the interval associ-

ated to C Partner2[10, 10].

C Partner2 [10,10]

state 0 = p11

state 1 = p12

state 2 = p01 p13 p14

state 3 = p13 p14 p21

state 4 = p02 p13 p14 p22

state 5 = Observer p02 p03 p13 p14 p23

state 6 = Observer p03 p13 p16 p23

state7 = Observer p03 p15 p16 p23

state 8 = Observer p03 p17 p23

state 9 = Observer p03 p18 p23

state 10 = Observer p19 p23

state 11 = Observer p04 p23

state 12 = End

state 13 = Observer p02 p03 p14 p15 p23

state 14 = p13 p16 p22

tised by Partner1, which is a maximum of 3 time

units between transitions OrderP2 and ShipP2.

The state classes generated is illustrated in Ta-

ble 2 below. We can see that the cooperation can

not always meet the temporal constraint, because

the two places ERROR and End are reachable.

This means that the temporal conformance can be

achieved under some additional restrictions.

Table 2: The Partner2 state classes for the interval associ-

ated to C Partner1[3, 3].

C Partner1 [3,3]

state 0 = p11

state 1 = Observer p01 p12

state 2 = Observer p12 p21

state 3 = Observer p12 p22

state 4 = Observer p12 p23

state 5 = ERROR p12 p23

state 6 = ERROR p12 p26

state 7 = ERROR p02 p12 p27

state 8 = ERROR p02 p03 p12 p28

state 9 = Observer p12 p26

state 10 = Observer p02 p12 p27

state 11 = Observer p02 p03 p12 p28

state 12 = p03 p13 p28

state 13 = p14 p28

state 14 = p04 p28

state 15 = End

state 16 = p13 p27

state 17 = Observer p12 p24

state 18 = ERotROR p12 p24

state 19 = Observer p12 p25

state 20 = ERROR p12 p25

4.4.3 Timed Veriﬁcation for Workﬂow

Negotiation

Besides analyzing whether a deadline requirement is

respected or n, it is also important to determine maxi-

mal bound under which the constraint is guaranteed to

be satisﬁed. In order to obtain the maximum limit al-

lowed, the tool LPT (Little Parametric Tool) (Godary,

2008) proposes an automatic analysis of the TPN

with added observer, while parameterizing the inter-

val associated to the transition modeling the deadline

constraint. This reachability analysis uses the state

classes graph generated automatically using the tool

TINA (Berthomieu and Vernadat, 2006).

In the previous example, Partner2 can not meet

Partner1’s temporal requirement. On our future

work, we will focus on model checking techniques to

determine necessary constraints to apply on the TPN

in order to meet the deadline. A communication pro-

tocol will be deﬁned between the two eventual part-

ners for exchanging necessary information. Even if

Partner2 is unable to modify its internal process and

add other timing constraints, he can send to Partner1

the necessary duration to deliver component P2. The

code below illustrates a part of LPT result for search-

ing the corresponding temporal constraint. It is shown

that cooperationcan always be held between Partner1

and Partner2 if the speciﬁed deadline between the

two activities OrderP2 and ShipP2 is greater than 7

time units.

---------------------------------------------

INITIAL PETRI NET : Partner2.ndr

ANALYSIS OF THE WORST DURATION BETWEEN

TRANSITIONS OrderP2 AND ShipP2

---------------------------------------------

THE BOUND VALUE IS : 7

Remark : this value is the upper bound,

it is never reached

---------------------------------------------

GRAPH SIZE : 17 classe(s), 19 transition(s)

---------------------------------------------

CALCULATION TIME : 1 seconds

---------------------------------------------

5 RELATED WORK

Time management in workﬂow-based processes has

been studied among several aspects: activities dura-

tion control, scheduling and prioritization, resources

management, etc... The ﬁrst important issue to deal

with is time modeling. In (Eder et al., 2000) and

(Eder and Panagos, 2000), time constraints are ex-

pressed using a timed workﬂow graph, which extends

worklow graphs by adding some temporal constraints

MODELING TIME CONSTRAINTS IN INTER-ORGANIZATIONAL WORKFLOWS

227

to each activity. In (Amirreza and Eder, 2008), the

authors adapted their approach for checking tempo-

ral consistency of inter-organizational workﬂows us-

ing workﬂow views. They present a timed work-

ﬂow graph approach in order to express the upper and

lower bound constraints of task execution. The tech-

nique enable partners to execute the IOW without vio-

lating temporal constraints such as explicitly assigned

deadlines.

Temporal constraints modeling have also been

studied in web service compositions research ﬁeld.

In (Diaz et al., 2007), temporal expectations are ex-

pressed using goal-oriented engineering. An exten-

sion of KAOS, an approach for goal oriented for-

mulation, is proposed and allow formal speciﬁca-

tion of timing requirements and automatic genera-

tion of counterexamples using model checking tech-

niques. In (Kazhamiakin et al., 2006), authors pro-

pose an extension of timed automata formalism to

specify global timing aspects of web service composi-

tions, called Web Service Timed State Transition Sys-

tems (WSTTS). Complex timed requirements can be

speciﬁed for modeling time intervals between events,

bounds or combinations of them. An algorithm is pro-

posed to compute the interval limits allowing to meet

the timing constraint. In (Benatallah et al., 2005),

business protocols are modeled as deterministic ﬁnite

state machines, and temporal abstractions of business

protocols are speciﬁed using timed transitions.

Our work is based on the CoopFlow approach and

guarantee that each partner can keep the critical part

of its business process private. Activities duration are

not ﬁxed. We plan to specify a communication proto-

col allowing partners to negotiate the speciﬁed dead-

lines according to their needs and their available re-

sources.

6 CONCLUSIONS

In this paper, we presented a time-oriented frame-

work for incorporating and veriﬁcation deadlines con-

straints in the context of Inter-Organizational Work-

ﬂows (IOWs). Even if the business behavior comple-

mentarity of the involved parties is validated, miss-

ing deadlines while delivering required services may

lead to a global failed execution. Based on the ex-

isting CoopFlow approach and using the Time Petri

Net theory, we proposed a method for expressing and

publishing sensible time deadlines, by each partner.

State reachability analysis is used for checking tem-

poral correctness of the resulting IOW. A further work

will concentrate on formulating a systematic method

for assuring the satisfaction and consistency of all

the published time constraints, within the context of

the global business process, while maintaining the

core advantage of CoopFlow; i.e. that each partner

can keep the critical parts of its business process pri-

vate. We have to prove that deadline local veriﬁ-

cation processes executed by partners can lead to a

deadline conformance in the resulting interconnected

workﬂow. Furthermore, we advocate that deadlines

should be negotiated. We will concentrate on specify-

ing a communication protocol between eventual can-

didates, which can lead to constraint negotiation in

order to achieve the cooperation.

REFERENCES

Amirreza, T. N. and Eder, J. (2008). Temporal consis-

tency of view based interorganizational workﬂows. In

2nd International United Information Systems Confer-

ence, pages 96–107, Klagenfurt, Austria.

Benatallah, B., Ponge, J., and Toumani, F. (2005). On tem-

poral abstractions of web services protocols. In CAiSE

Short Paper Proceedings, Porto, Portugal.

Berthomieu, B. and Diaz, M. (1991). Modeling and ver-

iﬁcation of time dependent systems using time petri

nets. IEEE Transactions on Software Engineering,

17(3):259–273.

Berthomieu, B. and Menasche, M. (1983). An enumerative

approach for analyzing time petri nets. In Proceedings

IFIP, pages 41–46, Paris. Elsevier Science Publishers.

Berthomieu, B. and Vernadat, F. (2006). Time petri nets

analysis with tina. In QEST: Third International Con-

ference on the Quantitative Evaluation of Systems

(QEST 2006), pages 123–124, Riverside, California,

USA.

Chebbi, I., Dustdar, S., and Tata, S. (2006). The view-

based approach to dynamic inter-organizational work-

ﬂow cooperation. Data Knowl. Eng., 56(2):139–173.

Chebbi, I. and Tata, S. (2005). CoopFlow: A framework for

inter-organizational workﬂow cooperation. In On the

Move to Meaningful Internet Systems Conferences,

pages 112–129, Agia Napa, Cyprus.

Chebbi, I. and Tata, S. (2007). Workﬂow abstraction for

privacy preservation. In Web Information Systems En-

gineering Workshops, pages 166–177, Nancy, France.

Diaz, G., Navarro, E., Cambronero, M.-E., Valero, V., and

Cuartero, F. (2007). Testing time goal-driven require-

ments with model checking techniques. In ECBS

’07: Proceedings of the 14th Annual IEEE Interna-

tional Conference and Workshops on the Engineering

of Computer-Based Systems, pages 503–514, Wash-

ington, DC, USA.

Eder, J., Gruber, W., and Panagos, E. (2000). Tempo-

ral modeling of workﬂows with conditional execution

paths. In DEXA ’00: Proceedings of the 11th Inter-

national Conference on Database and Expert Systems

Applications, pages 243–253, London, UK. Springer-

Verlag.

ICEIS 2010 - 12th International Conference on Enterprise Information Systems

228

Eder, J.and Panagos, E. (2000). Managing time in workﬂow

systems. In in Workﬂow Handbook 2001, Layna Fis-

cher (Ed.), Future Strategies Inc., 2001, pages 109–

132.

Godary, K. (2008). Lpt : Little parametric tool,

outil pour la validation d’une borne temprelle

param´etr´ee. Sixi`eme Conf´erence Internationale Fran-

cophone d’Automatique (CIFA’08).

Kazhamiakin, R., Pandya, P., and Pistore, M. (2006). Rep-

resentation, veriﬁcation, and computation of timed

properties in web. In Proceedings of the IEEE Inter-

national Conference on Web Services, pages 497–504,

Washington, DC, USA.

Klai, K., Tata, S., and Desel, J. (2009). Symbolic ab-

straction and deadlock-freeness veriﬁcation of inter-

enterprise processes. In Business Process Manage-

ment, 7th International Conference, pages 294–309,

Ulm, Germany.

Merlin, P. M. (1974). A study of the Recoverability of Com-

puting Systems. Technical report ♯58 (phd thesis),

Computer Science Department, University of Califor-

nia at Irvine.

Pezze, M. and Young, M. (1999). Time petri : A

primer introduction. In Tutorial presented at the

Multi-Workshop on Formal Methods in Performance

Evaluation and Applications, pages 41–46, Zaragoza,

Spain.

Tata, S., Klai, K., and M’Bareck, N. O. A. (2008).

Coopﬂow: A bottom-up approach to workﬂow coop-

eration for short-term virtual enterprises. IEEE T. Ser-

vices Computing, 1(4):214–228.

Toussaint, J., Simonot-Lion, F., and Thomesse, J.-P. (1997).

Time constraints veriﬁcation methods based on time

petri nets. In Proceedings of the 6th IEEE Workshop

on Future Trends of Distributed Computing Systems,

page 262, Washington, DC, USA.

MODELING TIME CONSTRAINTS IN INTER-ORGANIZATIONAL WORKFLOWS

229