PERFORMANCE GAIN FOR CLUSTERING WITH GROWING

NEURAL GAS USING PARALLELIZATION METHODS

Alexander Adam, Sebastian Leuoth, Sascha Dienelt and Wolfgang Benn

Department of Computer Science, Chemnitz University of Technology, Straße der Nationen 62, 09107 Chemnitz, Germany

Keywords:

Neural net, Growing neural gas, Parallelization.

Abstract:

The amount of data in databases is increasing steadily. Clustering this data is one of the common tasks in

Knowledge Discovery in Databases (KDD). For KDD purposes, this means that many algorithms need so

much time, that they become practically unusable. To counteract this development, we try parallelization

techniques on that clustering.

Recently, new parallel architectures have become affordable to the common user. We investigated especially

the GPU (Graphics Processing Unit) and multi-core CPU architectures. These incorporate a huge amount of

computing units paired with low latencies and huge bandwidths between them.

In this paper we present the results of different parallelization approaches to the GNG clustering algorithm.

This algorithm is beneﬁcial as it is an unsupervised learning method and chooses the number of neurons

needed to represent the clusters on its own.

1 INTRODUCTION

Knowledge Discovery in Databases (KDD) is the pro-

cess of preparing and processing data, and afterwards

the evaluation of the results that emerged from that

data. In the processing step of KDD often includes a

clustering. When using neural networks, in the train-

ing of these networks much time is spent, especially

when many neurons are used and huge amounts of

data have to be processed. Neural networks cannot

be utilized with too much data, as the training would

not ﬁnish in acceptable time. Parallelization seems to

be a way to minimize the computing time, needed for

such a training.

Modern computing platforms often comprise a

huge number of processing units. CPUs as well

as GPUs (Graphics Processing Units) (Szalay and

Tukora, 2008) and small desktop clusters (Reilly

et al., 2008) are examples for these platforms. They

are more and more in the scope of high performance

computing. With their huge amount of computing

units it seems reasonable to compare different paral-

lelization approaches with regards to how they scale

with an increasing degree of parallelism.

In our work we use the GNG algorithm, ﬁrst intro-

duced by Fritzke (Fritzke, 1995). The GNG offers the

possibility to only give an upper bound on the number

of neurons. It decides for itself, if that number has to

be exhausted. After the learning phase the connec-

tions between the neurons indicate clusters of data

vectors in relative proximity to each other. This

clustering property is then used in the ICIx (G¨orlitz,

2005), a new data base indexing structure.

2 RELATED WORK

Other approaches have been undertaken to parallelize

neural networks. Especially the longer known SOMs

(Kohonen, 1982) have been in the scope of these ef-

forts. In Labont´e (Labont´e and Quintin, 1999) the

neurons were distributed on different computers. It

was found, that for large numbers of neurons a nearly

linear speedup can be achieved. However, we do not

use that huge numbers of neurons but their results can

be an orientation for our work.

Another work has been done by Ancona (Ancona

et al., 1996). He examined parallelization on Plastic

Neural Gas networks. In these special networks the

dependencies between the neurons are not as strong

as in GNG networks. He distributes the training data

vectors on different computing nodes which each hold

only a fraction of the hole network. Through a special

update strategy he achieves a speedup in the number

of computing units used.

Another way to speed up especially hierarchical

264

Adam A., Leuoth S., Dienelt S. and Benn W. (2010).

PERFORMANCE GAIN FOR CLUSTERING WITH GROWING NEURAL GAS USING PARALLELIZATION METHODS.

In Proceedings of the 12th International Conference on Enterprise Information Systems - Artiﬁcial Intelligence and Decision Support Systems, pages

264-269

DOI: 10.5220/0002903502640269

 SciTePress

clustering is shown by G¨orlitz (G¨orlitz, 2005). His

clustering method ﬁrst does a coarse grained cluster-

ing. Afterwards, the found clusters are further split

up. This can be easily parallelized by distributing the

ﬁrst partition to as many nodes as clusters were found.

It has been shown, that the discovery of the ﬁrst parti-

tion is the bottle neck of this method. We are search-

ing for ways to speed up each learning step. That does

not touch the ability to distribute our approach with

this method.

Cottrell (Cottrell et al., 2008) shows a way to do

a batch learning with a neural gas network. There

the adaption of neurons only takes place after certain

steps of presentation of data to the neural net. During

these batches the neurons do not interact with each

other. Thus these regions of the algorithm offer a

source for parallelism. We ran tests using this method.

The results are also shown later in Section 4.

3 GNG-ALGORITHM

The goal of the GNG algorithm is to adapt a net of

neurons A to represent the distribution of a given data

set D . The data records in that set are presented to the

neurons. The neurons then adapt their internal ref-

erence vector to that of the given data record. After

a certain amount of steps λ, new neurons can be in-

serted or removed from the net. Neurons can have

edges between them, signaling that they belong to a

cluster. A cluster represents an area of the data space

with the records contained in it are relatively similar.

The formula symbols used also later on are shown in

Table 1. For a listing and further discussion of the

algorithm see (Fritzke, 1995).

3.1 Non-parallel Runtime

An adaption of that algorithm is used for the results in

this paper. This variant does not remove neurons from

the net to speed up the growth. It also decreases the

adaption rates when an integer multiple of λ cycles

is near. The last change has no impact on the overall

complexity of the algorithm and will be not further

regarded. The ﬁrst one decreases the computing time

and simpliﬁes the formulas later on.

The runtime of the single steps of the GNG algo-

rithm as found in (G¨orlitz, 2005) is shown in Table 2.

In (Adam et al., 2009) we already showed that the

runtime for one step of the learning algorithm is linear

in v and d. When accumulated over all steps, it shows

that the overall runtime is lineary depending on d, λ

and |D | but is quadratic in |A |.

Table 1: Symbol deﬁnitions.

symbol description estimated size

|D | number of data

records

millions

|A | maximum number of

neurons

typically 2-100

v number of neurons

per step

2 to |A |

d dimensionality of the

records and reference

vectors

up to 1500

λ insert and remove in-

terval for neurons

ca. 100

p number of processing

units used

1-500

Table 2: Runtime components for non-parallel case.

step runtime

compute distances v· d

ﬁnding winner and second v

insert edge 1

actualize error d

actualize winner d

actualize neighbors of winner v· d

adjust multiplier 2

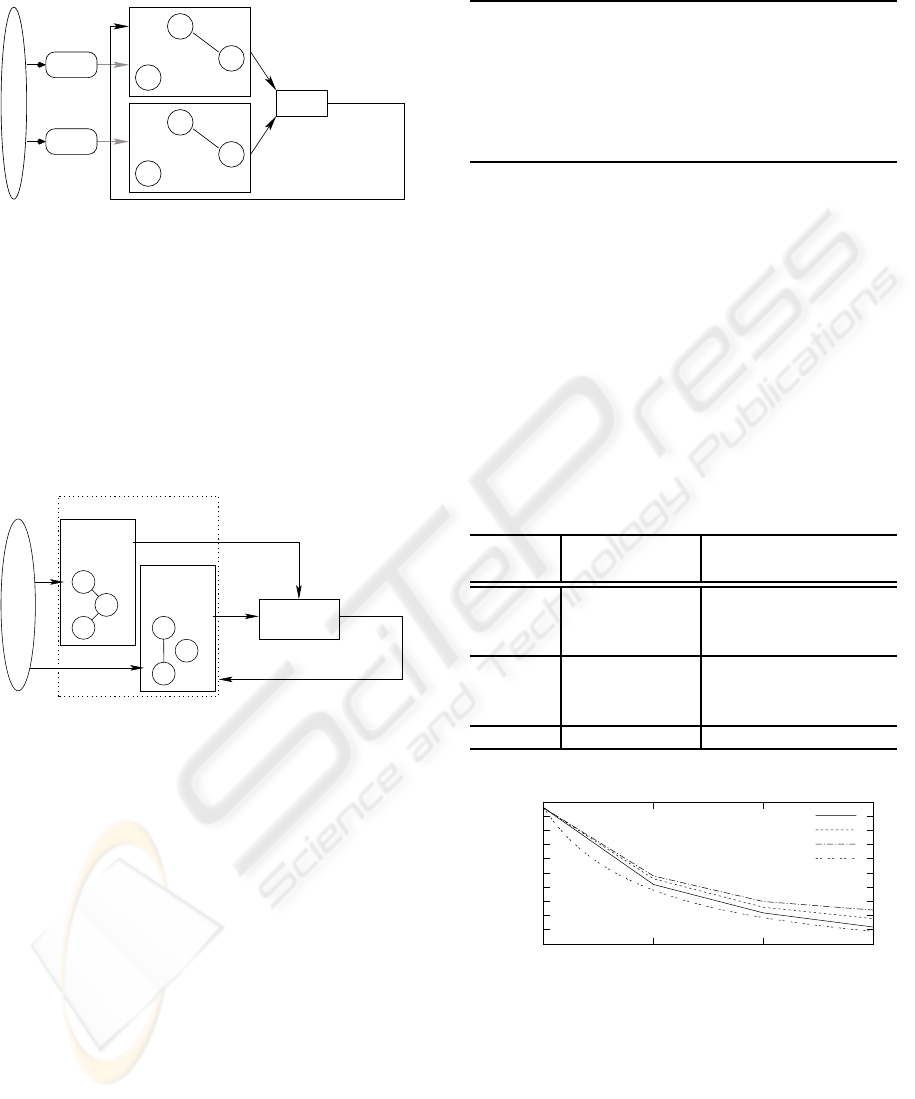
3.2 Data Parallelization

Figure 1 shows the scheme we used for our data par-

allelization approach. The data is partitioned and the

partitions then are learned by different independent

GNGs. After a certain amount of steps, these nets are

merged. Several synchronization or merge strategies

may be applied, particularly the following three were

used in this work:

1. Average: This method takes two neural nets and

does a position based average of the neurons

weight vector.

2. Batch: Another variant is to not move the neurons

during the training phase and accumulate their

movement in a variable ∆

for each net i. Out of

these ∆

an average is computed and this average

is applied to the neurons of the distributed nets.

3. GNG: The GNG algorithm itself can be applied

for the merge of two nets. The neurons of one net

are the data vectors the training of the other one.

Due to a cubic term we do not regard this method

further for our runtime estimations.

The equations for the runtime can be found in (Adam

et al., 2009). They show that a linear speedup in the

PERFORMANCE GAIN FOR CLUSTERING WITH GROWING NEURAL GAS USING PARALLELIZATION

METHODS

265

number of used computing units can be expected.

Input Data

Subset

GNG

Merge

distribute merged nets

Figure 1: Data parallelization scheme.

3.3 Neuron Parallelization

The neuron parallelization scheme is depicted in Fig-

ure 2. The neurons of the GNG are distributed to

different computing sites. The winner and second is

chosen in parallel and then all nets adjust their corre-

sponding neurons to the new input. In (Adam et al.,

2009) we showed, that the expected speedup is linear

in the number of computing units that are used.

Input Data

Computing

Unit

Computing

Unit

Global 1st &

2nd winner

GNG

Propagate 1st and 2nd winner

Figure 2: Neuron parallelization scheme.

4 EXPERIMENTAL RESULTS

We will now present the results of our work. First

we give an overview of the speedups gained with the

different parallelization methods on CPU and GPU.

After that we take a short look on the quality of the

data parallelization with regards to the utilized merge

strategy. For all tests the network parameters shown

in Table 3 were used.

As CPU we used an Intel

Core2 Q6600 (Quad

Core) processor at 2.4 GHz with 4 GB of DDR2-800

RAM. The GPU was an Nvidia GeForce 8800 GTX

SLI system with each graphics board equipped with

768 MB of GDDR3 RAM and a shader clock of 1350

MHz. The operating system was Windows Vista in

the 64 bit variant.

Table 3: Network parameters for the GNG learning.

insert interval λ

ins

= 10

winner adaption rate ε

= 0.1

neighbor adaption rate ε

= 0.002

error normalization value α = 0.001

dimensionality of the data

records

d = 96

maximal neuron number |A |

max

= 32

4.1 CPU-results

We started our tests using a CPU implementation. Ta-

ble 4 shows the results for the—theoretically better—

data parallelization. The last line shows the theoreti-

cal speedup. Aboveit is the real speedup gained. Syn-

chronization between the nets was done right before

inserting of a new neuron. It can be seen clearly, that

the speedup using the simple average method is the

best. It is nearly linear. A graphical representation

can also be found in Figure 3.

Table 4: Data parallelization computing times in sec-

onds.

merge # threads

method 1 2 3 4

runtime average 5.8 3.1 2.1 1.6

batch 5.8 3.3 2.3 1.9

GNG 5.8 3.4 2.5 2.2

speedup average 1.0 1.9 2.8 3.6

batch 1.0 1.8 2.5 3.1

GNG 1.0 1.7 2.3 2.6

speedup theoretically 1.0 2.0 3.0 4.0

1.5

2.5

3.5

4.5

5.5

1 2 3 4

runtime in seconds

number of threads

average

batch

GNG

theoretical

Figure 3: CPU Runtimes.

Table 5 shows the results using the neuron paral-

lelization approach. Barriers were used to synchro-

nize the different threads. The speedup—even with-

out measuring of the barriers—is not as big as at the

data parallelization. Including the barrier time, this

is because of the synchronization between the net-

work fractions that has to be done at every single data

ICEIS 2010 - 12th International Conference on Enterprise Information Systems

266

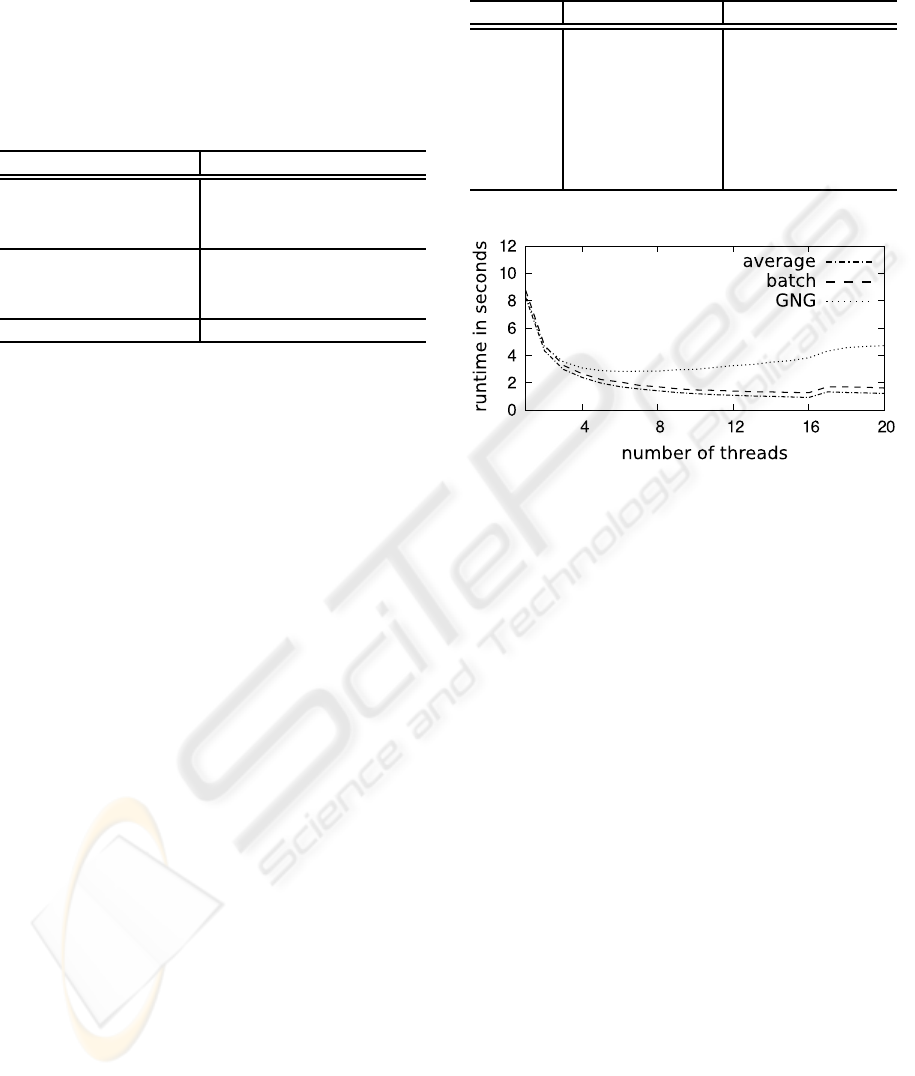
presentation. The speedup without the barriers is not

as good as the theory would predict. One reason for

this is, that the synchronization is not done parallelly.

Also, the serial components of the algorithm might be

larger than expected.

Table 5: Neuron parallelization computing times in

seconds.

#neuron threads 1 2 3 4

without barriers 5.8 3.7 2.6 2.3

with barriers 5.8 10.0 14.7 17.3

barrier overhead 0.0 6.3 12.1 15.0

speedup

without barriers 1.0 1.6 2.2 2.5

with barriers 1.0 0.6 0.4 0.3

theoretical speedup 1.0 2.0 3.0 4.0

So we conclude that on sole multi-core CPU sys-

tems the data parallelization approach is not only the-

oretically but also practically the most promising one.

4.2 GPU-results

The second test environment were GPUs. For the

Nvidia GPUs we had at our disposal, the CUDA

framework is the programming toolkit to use. Some

limitations exist for the parallelization on these GPUs.

The structure of the GPU is so that only distinct par-

titions of the processing units can communicate efﬁ-

ciently with each other. These partitions are called

streaming multi processors (SM) by Nvidia. The

SMs themselves consist of thread processors, that run

the actual computations. Neuron parallelization can

only happen inside such an SM due to this limitation.

(NVIDIA Corporation, 2009)

Further the GPU has dedicated memory areas, es-

pecially shared, constant, and global memory. The

constant respective texture memory are cached por-

tions of the global memory. The shared memory is

inside the SMs. These SMs also have a common reg-

ister set for all thread processors inside. The single

memory types are summed up in Table 6. Due to the

limited amount of memory, the maximum number of

neurons was 32 and the length of the vectors was lim-

ited to 96 inside one SM.

We used a hybrid parallelization due to the limi-

tations on the GPU. We distributed the data on differ-

ent SMs. Each SM then trained its own independent

net. The nets were synchronized using synchroniza-

tion methods described in Section 3.2. Inside each

SM we parallelized the neural net with neuron and

vector parallelization. Due to its complexity the CPU

computed the synchronization with the GNG-merge.

Table 6: Different memory types on Nvidia 8800

GTX GPU.

type size speed

constant ≤ 64kB fast (cached)

global whole memory slow

(uncached)

shared 16kB (16× 1kB) fast, inside SM,

comparable to reg-

isters

registers 8192 per SM very fast

Figure 4: Runtimes for parallelization on GPU.

Figure 4 shows the ﬁnal runtimes of the paral-

lelization using a mix of data, neuron, and vector

parallelization. It can be seen clearly, that using

only the neuron and vector parallelization, the GPU

is slower than the CPU implementation (one data

thread). When the data parallelization is added, the

runtimes on the GPU fall below that of the CPU.

Newer GPU generations have even more computing

units, so further speedup is expected.

4.3 Clustering Quality

The quality of the clustering was also of special inter-

est to us. That is because the data parallel approach

alters the result of the algorithm. As starting point

we took the original non-parallel variant of the GNG

algorithm. We presented the same input data, origi-

nating from Fritzke (Fritzke, 1995), to all algorithms.

Figure 5a shows the results of the non-parallel variant.

The clusters are well covered by the neurons.

The results of the batch variant are shown in Fig-

ure 5b and present the best merge method—in therms

of clustering quality—up to this point of our research.

The clusters are not as well covered as in the non-

parallel variant of the algorithm, but still show the

structure of the clusters.

We also evaluated the merge methods—using

again the GNG algorithm and the average value of the

PERFORMANCE GAIN FOR CLUSTERING WITH GROWING NEURAL GAS USING PARALLELIZATION

METHODS

267

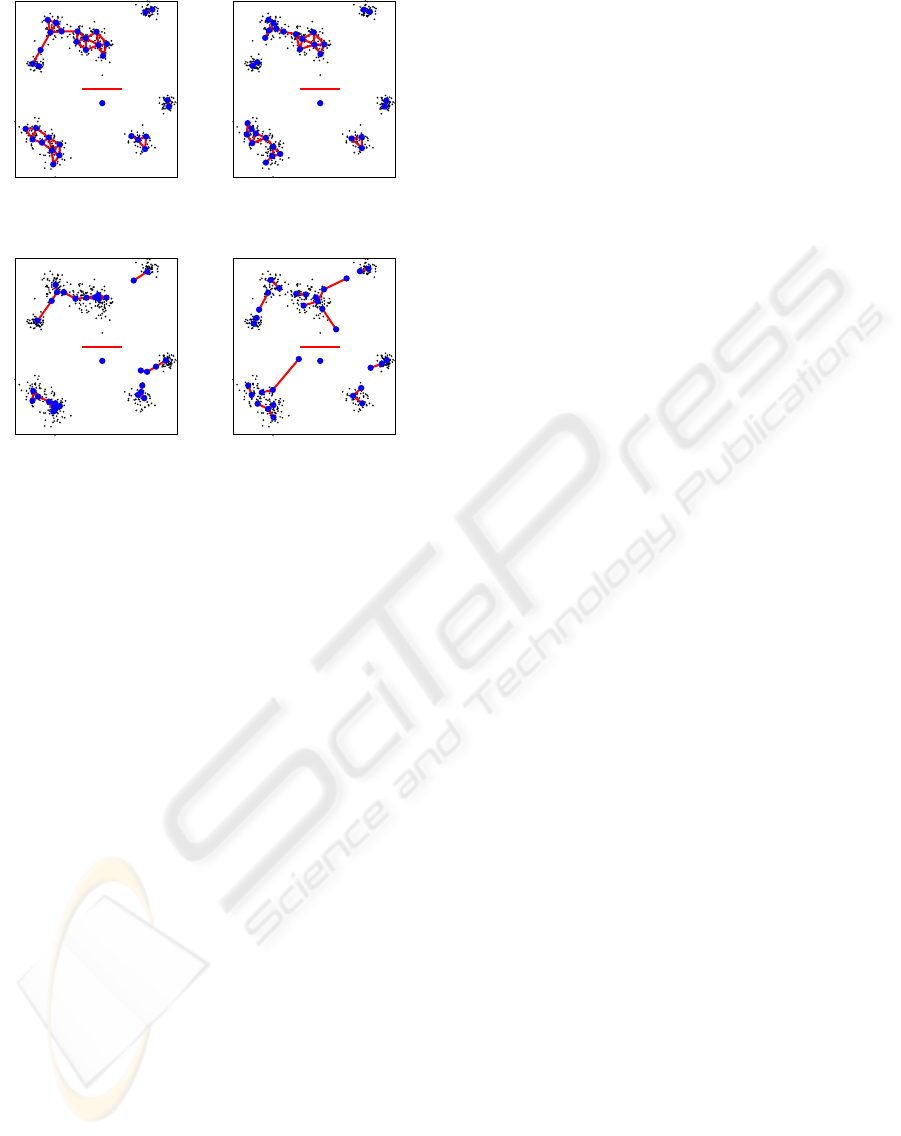
Data

Edge

Neuron

(a) original GNG

Data

Edge

Neuron

(b) batch-merge GNG

Data

Edge

Neuron

Data

Edge

Neuron

(d) average-merge GNG

Figure 5: Training results.

neurons. Their results are shown in Figures 5c and

5d. The GNG-merge lets the neurons collapse. This

is because for the merge only the reference vectors of

the neurons are used. At the beginning of the train-

ing, these vectors are in the center of the data vectors

and are not adapted fast enough to later represent the

data vectors. The average-merge scattered the neu-

rons and broke up clusters. This is because the neu-

rons are merged according to their number, not their

position. So neurons belonging to different clusters

could be merged. For the GNG-merge, we will try to

alter some of the parameters to get better results, but

for now the batch-merge is our favorite.

To measure the quality of the clustering, different

methods were proposed. We used the Dunn (Dunn,

1974), Goodman-Kruskal (Goodman and Kruskal,

1954), C (Hubert and Schultz, 1976), and Davies-

-Bouldin (Davies and Bouldin, 1979) index. The

quality of the clustering only changes when data par-

allelization is used. This is the only method that

changes the original GNG algorithm. In our cases this

meant a decrease—dependingon the merge method—

of the clustering quality.

Using the Goodman-Kruskal index all merge

methods are near the optimum of 1, only the GNG

method (using 16 data threads) is slightly worse. This

means that pairs of neurons inside one cluster mostly

have smaller distances between them than pairs of

neurons of different clusters. The other index operat-

ing on the distances between neurons—the C index—

showed no differentiation. The GNG method again

showed a slightly worse behavior at 16 data threads.

The Dunn index, stating that clusters are well dif-

ferentiated, is overall low. The best values for this in-

dex are gotten with the non-parallel algorithm. Then

using data parallelization the batch merge method

showed the best results at approximately 0.15 (values

greater than 1 are good).

Finally the Davies-Bouldin index was used. It is

a measure for the compactness of the clusters in rela-

tion to their distance. The batch and the GNG merge

method are at the level of the non-parallel GNG al-

gorithm. Only the average merge method showed de-

teriorating values with an increasing number of data

threads.

5 CONCLUSIONS

We have shown, that—theoretically and also

practically—a performance gain of the GNG algo-

rithm through parallelization can be achieved. Data

parallelization has the most potential but also has

its pitfalls in the synchronization methods used. We

also showed that for the used GPU architecture a

further sub-parallelization on neuron and vector level

is advantageous.

We will further explore the possibilities of the

parallelization of the GNG algorithm with regards to

other parallel architectures such as clusters. The up-

coming multi-core CPUs and GPUs, which promise

much larger numbers of computing units are in our

focus, too. (Intel, 2007) (Kowaliski, 2007) (Etengoff,

2009) (Sweeney, 2009)

REFERENCES

Adam, A., Leuoth, S., and Benn, W. (2009). Perfor-

mance Gain of Different Parallelization Approaches

for Growing Neural Gas. In Perner, P., editor, Ma-

chine Learning and Data Mining in Pattern Recogni-

tion, Poster Proceedings.

Ancona, F., Rovetta, S., and Zunino, R. (1996). A Parallel

Approach to Plastic Neural Gas. In Proceedings of the

1996 International Conference on Neural Networks.

Cottrell, M., Hammer, B., and Hasenfuß, A. (2008). Batch

and median neural gas. Elsevier Science.

Davies, D. L. and Bouldin, D. W. (1979). A Cluster Sepa-

ration Measure. Pattern Analysis and Machine Intel-

ligence, IEEE Transactions on, PAMI-1(2):224–227.

Dunn, J. C. (1974). Well separated clusters and optimal

fuzzy-partitions. Journal of Cybernetics, 4:95–104.

Etengoff, A. (2009). Nvidia touts rapid GPU performance

boost. http://www.tgdaily.com/content/view/43745/

135/.

ICEIS 2010 - 12th International Conference on Enterprise Information Systems

268

Fritzke, B. (1995). A Growing Neural Gas Network Learns

Topologies. In Advances in Neural Information Pro-

cessing Systems 7, pages 625–632. MIT Press.

Goodman, L. A. and Kruskal, W. H. (1954). Measures of

Association for Cross Classiﬁcations. Journal of the

American Statistical Association, 49(268):732–764.

G¨orlitz, O. (2005). Inhaltsorientierte Indexierung auf Basis

k¨unstlicher neuronaler Netze. Shaker, 1st edition.

Hubert, L. and Schultz, J. (1976). Quadratic Assignment

as a General Data Analysis Strategy. British Journal

of Mathematical and Statistical Psychology, 29:190–

241.

Intel, C. (2007). Intel’s teraﬂops research chip.

http://download.intel.com/pressroom/kits/Teraﬂops/

Teraﬂops Research Chip Overview.pdf.

Kohonen, T. (1982). Self-organized formation of topolog-

ically correct feature maps. Biological Cybernetics,

43(1):59–69.

Kowaliski, C. (2007). AMD unveils microprocessor strat-

egy for 2009. http://www.techreport.com/discussions

.x/12945.

Labont´e, G. and Quintin, M. (1999). Network Parallel Com-

puting for SOM Neural Networks. Royal Military

College of Canada.

NVIDIA Corporation (2009). NVIDIA CUDA Compute

Uniﬁed Device Architecture - Programming Guide.

Reilly, M., Stewart, L. C., Leonard, J., and Gingold, D.

(2008). SiCortex Technical Summary. Technical sum-

mary, SiCortex Incorporated.

Sweeney, T. (2009). The End of the GPU Roadmap.

http://graphics.cs.williams.edu/archive/SweeneyHPG

2009/TimHPG2009.pdf.

Szalay, T. and Tukora, B. (2008). High performance com-

puting on graphics processing units. Pollack Period-

ica, 3(2):27–34.

PERFORMANCE GAIN FOR CLUSTERING WITH GROWING NEURAL GAS USING PARALLELIZATION

METHODS

269