EFFICIENT SEMI-AUTOMATIC MAINTENANCE OF MAPPING

BETWEEN ONTOLOGIES IN A BIOMEDICAL ENVIRONMENT

Imen Ketata, Riad Mokadem, Franck Morvan and Abdelkader Hameurlain

Institut de Recherche en Informatique de Toulouse IRIT, Paul Sabatier University

118 Route de Narbonne F-31062, Toulouse Cedex 9, France

Keywords: Biomedical Data Sources, Data Integration, Ontology, Mapping.

Abstract: In dynamic environments like data management in biomedical domain, adding a new element (e.g. concept)

to an ontology O

requires significant mapping creations between O

and the ontologies linked to it. To

avoid this mapping creation for each element addition, old mappings can be reused. Hence, the nearest

element w to the added one should be retrieved in order to reuse its mapping schema. In this paper, we deal

with the existing additive axiom which can be used to retrieve this w. However, in such axiom, the usage of

some parameters like the number of element occurrence appears insufficient. We introduce the calculation

of similarity and the user’s opinion note in order to have more precision and semantics in the w retrieval. An

illustrative example is presented to estimate our contribution.

1 INTRODUCTION

Computer science applications in biomedicine

accumulate important data volume by the

establishment of huge network of heterogeneous and

autonomous data sources distributed all over the

world. Every day new sources are published.

Consequently, the major challenge is to present a

view of these sources to help users accessing and

integrating them. There are three approaches in the

literature: navigational (Davidson et al., 1995), data

warehouse (Hammer and Schneider, 2003) and

mediation (Hernandez and Kambhampati, 2004).

The navigational approach is not widely used since

the difficulty of keeping up to date its entire static

links on which user leans to navigate between the

various web pages. Data warehouse deals with

copying and updating all the data in all sources and

integrating them into a local warehouse. However,

this is not easy, especially in a domain where

sources are added almost in a daily way with rather

important volumetric, e.g. the biomedical domain.

Finally, the mediation approach surmounts the

difficulties confronted in the previous approaches,

particularly those of update, by using the view and

global schema principle with adopting the mediator-

wrapper architecture.

In previous studies the principle of mediation

often relies on a global schema. Whereas, when such

type of schema is used, resolving several synonymy

and polysemy problems, which are more crucial in

the biomedical domain, is a difficult target. This

problem brings forth other methods which describe

the source contents in a more explicit way to assess

to its meanings, e.g. ontologies (Jonquet et al.,

2008). Developing a standard and global ontology is

the perfect solution for presenting (schematically) all

sources in a unique and homogeneous format.

However, until today, developing such ontology has

been seen as a very difficult task (Aumueller et al.,

2005). Hence, a solution emerged: the domain

ontology (Karmakar, 2007), so that, each domain is

presented by a domain ontology.

To move from one domain to another, we have to

go by some correspondence relations between them.

Establishing this type of communication means

creating connections (correspondences) between

domain ontologies what we call: mapping (Choi et

al., 2006, Aumueller et al., 2005 and Drumm et al.,

2007). In dynamic environments, it is very difficult

to maintain this mapping up to date.

Given the dynamic nature of biomedical

environment and the very rapid evolution of data

amount, creating and maintaining this mapping up to

date manually is expensive, slow and complicated to

achieve. Hence, researchers have studied to

automate this process. However, creating and

257

Ketata I., Mokadem R., Morvan F. and Hameurlain A. (2010).

EFFICIENT SEMI-AUTOMATIC MAINTENANCE OF MAPPING BETWEEN ONTOLOGIES IN A BIOMEDICAL ENVIRONMENT.

In Proceedings of the 12th International Conference on Enterprise Information Systems - Databases and Information Systems Integration, pages

257-262

DOI: 10.5220/0002905702570262

 SciTePress

maintaining the mapping with a full automatic way

without expert’s intervention is hard to realize

(Aumueller et al., 2005). Indeed, semi-automatic

solutions can automate mapping updating task with

reduced expert’s effort. Several studies have

emerged in this context, such as COMA++

(Aumueller et al., 2005) and QuickMig (Drumm et

al., 2007).

Keeping the mapping up to date, after an element

addition (e.g. concept), requires creating mapping

between the newly added element and existing ones.

Reusing existing mappings can avoid the creation of

a new mapping at each element addition. For this

reason, it seems natural to seek the most similar

element to that added in order to reuse its mapping.

Having an effective selection of this similar element

means having essentially a high semantic level in

ontologies and its mapping schemas (Drumm et al.,

2007 and Choi et al., 2006). This means in others

words, introducing concepts and mapping relations

in a more explicit and accurate way. To deal with

this semantic, some researchers rely on similarity

between elements (Couto et al., 2007). Other

approaches deal with the similarity between graphs

(Melnik et al., 2002), semantic similarity relations

between descriptions in ontologies (Hakimpour and

Geppert, 2002) and using the word similarity to

semi-automatic element generation in ontologies

(Weeds and Weir, 2005). The first two approaches

are used for schema and relation similarities. The

third one, proposed in (Weeds and Weir, 2005) is the

most appropriate to deal with similarity between two

concepts (words). It relies on theorem called

additive axiom to retrieve the nearest word to a

newly added one. This axiom calculation is based

primarily on the common features between the

added and the old word and secondly on the

importance of the old word. This importance is

measured by the number of word occurrence

(appearance). Although the occurrence number is

necessary to calculate the word importance, it is not

sufficient in some cases since there are several

words appearing many times while they do not have

an importance. Thus, addition of other parameters in

the word importance calculation should be

examined. In this paper, we propose to add two

parameters in order to have more precision and

semantics in the calculation of the word importance

in additive axiom. Precisely, we introduce the

similarity calculation for more accuracy in the

additive axiom results. We involve also the opinion

of the users as they might be experts in the

biomedical domain (e.g. doctor, biologist). So we

can benefit from the user’s experience and

knowledge to evaluate the importance of a word.

Subsequently, the addition of these two parameters

(similarity calculation and user’s opinion) can lead

to a more accurate and meaningful selection for the

nearest word to the added one for a better semi-

automatic mapping maintenance.

In the second section, we define basic concepts

in data integration for the biomedical domain. In the

third section, we introduce our contribution. After

that, to validate our work we evaluate it by an

illustrative example. The final section contains

concluding remarks and future perspectives.

2 BASIC CONCEPTS IN DATA

INTEGRATION FOR THE

BIOMEDICAL DOMAIN

The very fast evolution of the data sources in a

dynamic environment generates several complex

problems which are much more complicated in the

biomedical field since the huge volumetric of data

sources and their number evolving over the time in a

very fast way. This requires a big storage capacity

infrastructure, e.g. Grid.

The use of ontology (which is more suitable than

a global schema, as showed earlier), is a solution in

which several researchers have been interested

(Hernandez and Kambhampati, 2004). However, it is

very difficult to have a standard ontology

representing the entire biomedical domain. One

solution emerges, that is to present (conceptualize)

each sub-domain of biomedical domain by a domain

ontology (Karmakar, 2007). In this paper, we

represent each biomedical sub-domain by a domain

ontology. To integrate data sources related at each

domain ontology, mediation is the most suitable

approach. Therefore, at each domain ontology, a

number of mediators is associated. The passage from

one mediator to another in the same sub-domain is

not a problem since the communication between

them is established through common rules. This is

not the case with two mediators belonging to

different sub-domains. Besides, to be able to link

semantically concepts in this last case, we must

establish the mapping between domain ontologies.

Various research works have focused on this context

dealing with the semantic heterogeneity. In this

paper, we are especially interested in the work of

(Weeds and Weir, 2005) which helped to maintain

the ontology mapping.

The mapping involves integrating a set of

independently developed schemas and/or ontologies

ICEIS 2010 - 12th International Conference on Enterprise Information Systems

258

into a single one (Drumm et al., 2007 and Madhavan

et al., 2001). There are two kinds of mapping: (i) the

mapping between an ontology and the schema or the

local ontology related to a data source (Choi et al.,

2006 and Silva and Rocha, 2003) and (ii) the

mapping between ontologies (Weeds and Weir, 2005

and Doan et al., 2002). The first type allows

communication between an ontology and its sources.

In the second type, ontologies are connected two by

two without taking into account the type of the

topology allowing so more autonomy.

At each new element addition w’ (concept), an

appropriate mapping must be established. Reusing

old mapping related to the nearest element w to the

added one w’ can avoid recreating this mapping at

each insertion as we noted earlier. So, the proximity

between the added element and existing ones must

be calculated to find the nearest one. Diverse studies

are interested in this problem. We quote for example

those which are based on the similarity calculation:

(Melnik et al., 2002, Hakimpour and Geppert, 2002

and Weeds and Weir, 2005). This last work deals

with the distributional similitude and the semantic

similarity between elements. It is exactly interested

in the applicative domain for automatic ontology

generation (e.g. Thesaurus). Specifically, it deals

with the problem of retrieving similar distributed

words to the newly added one. It uses, in particular,

theorem called additive axiom to calculate the

proximity between two words. This means finding

the nearest word to the added one in order to choose

the suitable mapping schema, and thus, reusing it to

conceive the new word mapping. Let’s present this

additive axiom in what follows. Let the precision

add

be the result returned from the calculation of the

proximity between two words: w and w’, with taking

into account the common features between these two

words, P

add

є [0, 1]. This precision is calculated

according to the following formula:

(w, w’) = ∑

(

w’

)

(w, c)

(1)

∑

(

)

(w, c)

The weight D determines which word occurrence is

important enough to be presented in its description.

There are various weight functions, e.g.:

1 if P(c|w) > 0,

(2)

(w, c) = 0 otherwise.

With P(c|w) the probability of the w occurrence.

Let F(w) presents the set of all the properties of a

word w. F(w) = {c: D

type

(w, c) > 0}, with D the

weight associated to w and c the occurrence number

(word appearance number in the results returned by

the already executed users’ queries).

The TP(w, w’) corresponds to the shared properties

between two words: w and w’ (TP(w, w’) = F(w) ∩

F(w’)). The precision P

add

allows to find w: the

nearest word to the newly added word w’. It

calculates the proximity between this w’ and each

word w

of existing words. The calculation of this

proximity is based on two basic principles: (i) the

common features between two words and (ii) the

importance of the old word. The next section shows

how these parameters are insufficient for an

effective retrieval of the nearest word.

3 PRECISION AND SEMANTICS

IN ADDITIVE AXIOM

The calculation of the word importance in the

additive axiom introduced in (Weeds and Weir,

2005) is relaying on some parameters like

occurrence number in executed query’s results. But,

since the number of useless word occurrence is

sometimes important, the word importance

calculation using only this occurrence number

parameter turns out insufficient. To solve this

problem, it is necessary to introduce other

calculation parameters. Thus, we propose to add two

other parameters (i) the similarity calculation

(degree) between two words (the added word and an

existing one) and (ii) the consideration of the user’s

opinion note (user’s satisfaction degree) associated

to every word with respect to the old returned users’

query results.

The similarity between two words w and w’ is

calculated by measuring the distance between them

(w, w’) (Zhong et al., 2002). To calculate this

distance, we consider the place (position) of words

with respect to its root ccp (Zhong et al., 2002):

(w, w’) = d

(w, ccp) + d

(w’, ccp) with d

(w,

ccp) = milestone(ccp) – milestone(w) and milestone

is the word position value: milestone(n) = 1 / 2kl(n)

(with k the speed by which the value decreases along

the hierarchy and l(n) indicates the depth of the word

in the hierarchy (e.g. l(cpp) = 0)). Then, the

similarity calculation formula is: Sim

(w, w’) = 1 –

(w, w’); with 0 < Sim

< 1. This parameter can

add more accuracy at the selection of the nearest

word to the added one.

Besides, for the users’ opinion note parameter,

old queries’ results should be used to benefit from

the domain experts’ knowledge. So, the integration

system has to allow the user introducing his opinion.

Therefore, each user notes his satisfaction degree

related to each word received in his queries’ results.

EFFICIENT SEMI-AUTOMATIC MAINTENANCE OF MAPPING BETWEEN ONTOLOGIES IN A BIOMEDICAL

ENVIRONMENT

259

The reuse of these results can help to improve the

importance word calculation by returning a more

significant selection results. The value of a user’s

opinion note for a given word is the average of all

users’ opinions related to this word (the sum of all

users’ opinions values divided by users’ number):

= Avg((S

)i), 0 < i < n; with n the number of

users. This S

value is always included between 0

and 1 (0 < S

< 1) since the precision P

add

can not

exceed 1. Hence, after a user’s query execution, a

value is associated to every word in this query which

is added precisely to the description of the word.

Then, after the insertion of these two new

parameters, the new axiom formula will be:

add

(w, w’) = ∑

TP(w, w’)

type

(w, c) * Sim

(w, w’) * S

∑

F(w )

type

(w, c)

(3)

The calculation of “Sim

(w, w’) * S

” add more

precision to define the nearest word to the added one

in a more semantic way. When we associate this

calculation to the other which calculates the

proximity between two words in initial P

add

, we can

conclude that our solution brings a more accurate

answer in the selection of the nearest word to the

added one.

In the following section, we show through an

illustrative example that these two added parameters

allow a better reliability. We also show that the use

of the initial additive axiom is not sufficient in the

case of important occurrence number of useless

words. So, we allow reusing the mapping of the

nearest element found in a reliable way.

4 ILLUSTRATIVE EXAMPLE

We adopt the additive axiom presented in (Weeds

and Weir, 2005) and add modifications (addition of

similarity calculation and the user’s opinion note) to

adapt it to our requirements. Indeed, the axiom

which we have just defined calculates the precision

of every added word with respect to each existing

word. We have to look for the nearest word to the

added one by defining the most suitable additive

model (model generated by the additive axiom for

the word and relation additions between them). We

note this as: Max {P

add

, w’)} with i all existing

words.

We explain the initial additive axiom limit as

well as the improvements that it will take through an

illustrative example.

4.1 Application Example of Sim

and

Parameters

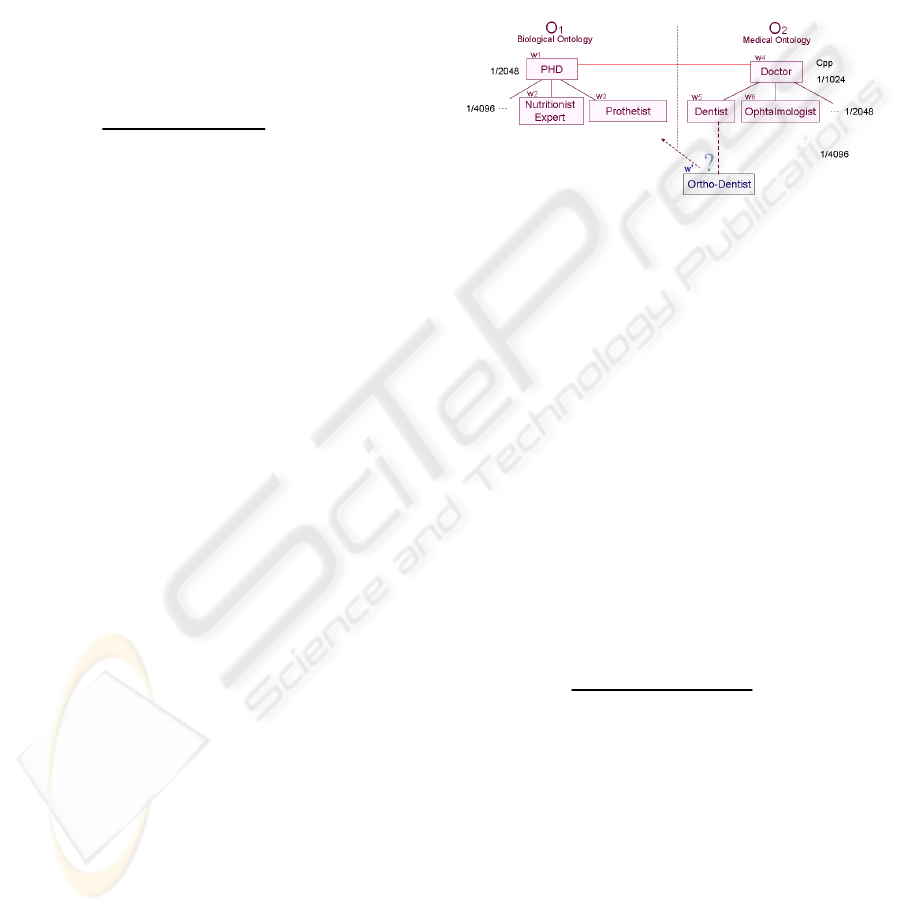
Let O

be a first ontology of biological domain and

a second one of medical domain.

Let w’: ‘Ortho-Dentist’ be the newly added word

and w

be the set of existing words in both

ontologies O

and O

: w

: ‘PHD’, w

: ‘Nutritionist

Expert’, w

: ‘Prosthetiste’, w

: ‘Doctor’, w

‘Dentist’, w

: ‘Ophtalmologist’.

Figure 1: Word Addition.

Finding the nearest word to ‘Ortho-Dentist’

means calculating the proximity between w’

(‘Ortho-Dentist’) and every word w

by P

add

precision formula.

First, let’s apply the initial axiom: (1).

So, let’s begin by calculating the proximity

between the added word ‘Ortho-Dentist’ (w’) and a

word among the existing words such as ‘Prosthetist’

type

, c) = 1, represents the weight associated

with the word w

since the number of its occurrence

can be important.

Let ∑F(w

) = 10, be the w

features (attributes)

and ∑F(w’) = 7, be the w’ features.

TP(w

, w’) = F(w) ∩ F(w’), ∑TP(w

, w’) = 4,

which represents the common features between w

and w’.

Then the precision calculated would be:

add

, w’) = ∑

TP(w3, w’)

type

, c) = 0.40000.

∑

F(w3)

type

, c)

By the same way we obtain also the following

precisions for the other words:

add

(w1, w’) = 0.10041, P

add

(w5, w’) = 0.39999 and

add

(w4, w’) = 0.21551.

Now, let’s apply the new axiom (extended) by

taking into account both added parameters.

We begin by looking for the nearest word to

‘Ortho-Dentist’. Let’s take the example of the word

‘Doctor’ (w

) and let’s calculate P

add

, w’). We

begin by calculating the distance as we mentioned

before:

(Ortho-Dentist, Doctor) = d

, w’)

= d

, w

) + d

(w’, w

)

ICEIS 2010 - 12th International Conference on Enterprise Information Systems

260

= (1 / 1024 – 1 / 4096) + (1 / 1024 – 1 / 2048)

= 0.00073.

Then similarity will be:

Sim

, w’) = 1 – 0.00073 = 0.99878.

The similarity calculation of these three other

words (w

: ‘Dentist’, w

: ‘Physician’ and w

‘Prosthetist’) is measured by the same manner as w

so we obtain: Sim

, w’) = 0.99878, Sim

, w’)

= 0.99927 and Sim

, w’) = 0.99854.

Let S

= 0.7, S

= 0.6, S

= 0.5 and S

= 0.6.

The S

values are chosen little close but different

and not too small voluntarily to highlight the

influence of the user’s opinion in our P

add

precision

calculation. This calculation does not focus only on

the user’s opinion, but also on the similarity

calculation which we added and the calculation of

common features between the two words already

presented in the initial axiom. So, the values of S

should not be also very big to avoid hiding the effect

of these two other parameters.

We can note that S

and S

have the same value

which is chosen voluntarily to show the influence of

the similarity in our calculation.

At last let’s apply the totality of the new axiom:

add

, w’) = 0.10041*0.99878*0.7 = 0.07020,

add

, w’) = 0.39999*0.99876*0.6 = 0.23969,

add

, w’) = 0.21551*0.99926*0.5 = 0.10767 and

add

, w’) = 0.40000*0.99853*0.6 = 0.23964.

4.2 Comparison between Initial and

New Axiom Results

In the following, we detail the values obtained for

each word with respect to the newly added word.

We mention the values obtained by the initial

additive axiom and those obtained by adding the two

new parameters. We get so the following table:

Table 1: Comparison of axioms’ results.

Initial Axiom’s

add

New Axiom’s

add

PHD (i = 1) 0.10041 0.07020

Dentist (i = 5) 0.39999

0.23969

Doctor (i = 4) 0.21551 0.10767

Prosthetist (i = 3)

0.40000

0.23964

Using the initial additive axiom, the nearest word

to w’ (‘Ortho-Dentist’) is w

(‘Prosthetist’) which

corresponds to the maximal value of P

add

precision

(Max(P

add

, w’)) = P

add

, w’)). Whereas, the

introduction of similarity and user’s opinion

parameters makes w

(‘Dentist’) appears as the

nearest word to w’ (Max(P

add

, w’)) = P

add

w’)). This last result is closer to the reality, since

‘Ortho-Dentist’ is a speciality of ‘Dentist’ and they

are both doctors, which is not the case of

‘Prosthetist’. In other words, contrary to the initial

axiom, the implementation of the extended axiom

formula allows to realize that the word ‘Prosthetist’

does not be the semantically nearest word to the

added one ‘Ortho-Dentist’ although its occurrence

number is important in the users’ query results.

Indeed, the calculation of “Sim

(w, w’)” adds

more precision to define w as the nearest word to w’.

The calculation of S

refines the selection of the

word w in a semantic way, by using the old queries’

results corresponding to each word w.

The mapping schemas of w are selected to reuse

them in creating the w’ mapping schema.

Consequently, the additive model of w’ is created in

an efficient way.

5 RELATED WORK

Several research works focus more and more on the

schema mapping thanks to the big interest accorded

to the integration and so to the mapping schema. The

mapping can decline into three classes (Choi et al.,

2006): (i) mapping between domain ontology and

data source local ontologies, (ii) mapping between

local ontologies and (iii) mapping for ontology

merging.

Managing this mapping in an automatic way

constitutes a real challenge because of the enormous

quantity of biomedical data sources. As it is

explained earlier, a semi-automatic mapping can

reduce the users’ effort (Aumueller et al., 2005). The

already existing mapping schemas can be shared and

reused to avoid recreation tasks, e.g. QuickMig

(Drumm et al., 2007) which uses new techniques for

the exploitation of the existing mappings’ schemas

by detecting not only the correspondence elements

but also the mapping’s expressions. The example of

COMA (Do and Rahm, 2002) is also based on the

principle of old mapping reuse, combining several

techniques of mapping. This system was extended in

order to support schemas and ontologies written with

various format types, what gave birth to COMA++

(Aumueller et al., 2005). This last system adopts a

new mapping technique for ontologies and reduces

the execution time. To choose the most suitable

mapping schema for the added element, the nearest

element to the newly added one has to be selected.

Then, its mapping schema can be reused (Madhavan

EFFICIENT SEMI-AUTOMATIC MAINTENANCE OF MAPPING BETWEEN ONTOLOGIES IN A BIOMEDICAL

ENVIRONMENT

261

et al., 2001, Do and Rahm, 2002 and Weeds and

Weir, 2005). This last study uses the similarity and

word importance calculation between words to

choose the nearest element.

6 CONCLUSIONS

In this paper we have dealt with the retrieval of the

nearest element to an added one in order to reuse its

mappings. Therefore, we have extended an existing

additive axiom formula by introducing new

parameters for the effective retrieval of the nearest

element (word) to the added one. First, we introduce

the similarity calculation between the added word

and existing ones. This enables more precision and

accuracy in the calculation of the semantic proximity

between two words. Second, we take into account

the users’ opinions to measure the importance of a

word with respect to its semantic value. This allows

emphasizing the semantic importance of concepts

(words) with respect to experts’ opinion. The

introduction of these two parameters allows

covering more semantic heterogeneity between data

sources of the biomedical domain. In consequence, it

allows an efficient semi-automatic mapping

maintenance. Such mapping can be very useful for

diverse research studies which are interested in the

integration of heterogeneous data sources distributed

on large scale. We validate our method by an

illustrative example of the extended additive axiom

including the proposed two parameters. We show

that results obtained by our method are closer to the

reality than those found by the initial axiom.

For future works, we are planning to design a

better evaluation of our contribution by relying on

real experiments. We can also test the extended

additive axiom when thousand of heterogeneous

types of data are added to diverse domain

ontologies.

REFERENCES

Aumueller, David, Do, Hong-Hai, Massmann, Sabine and

Rahm, Erhard, 2005. Schema and Ontology Matching

with COMA++. ACM SIGMOD International

Conference on Management of Data, Baltimore,

Maryland.

Choi, Namyoum, Song, Il-Yeol and Han, Hyoil, 2006. A

Survey on Ontology Mapping. ACM SIGMOD

Record.

Couto, Francisco M., Silva, Mario J., Coutinho and Pedro

M., 2007. Measuring semantic similarity between

Gene Ontology terms. Data & Knowledge

Engineering Journal.

Davidson, S., Overton, C. and Buneman, P., 1995.

Challenges in Integrating Biological Data Sources.

Journal of Computational Biology.

Do, Hong-Hai and Rahm, Erhard, 2002. COMA-A system

for flexible combination of schema matching

approaches. VLDB Conference, Hong Kong, China.

Doan, AnHai, Madhavan, Jayant, Domingos, Pedro and

Halevey, Alon, 2002. “Learning to Map between

Ontologies on the semantic Web”. WWW Conference,

Honolulu, Hawaii, USA.

Drumm, Christian, Schmitt, Matthias and Do, Hong-Hai,

2007. QuickMig-Automatic Schema Matching for

Data Migration Projects. ACM CIKM Conference,

Lisbon, Portugal.

Hakimpour, Farshad and Geppert, Andeas, 2002. Global

Schema Generation Using Formal Ontologies.

International Conference on Conceptual Modeling,

Finland.

Hammer, J. and Schneider, M., 2003. Genomics Algebra:

A New, Integrating Data Model, Language, and Tool

Processing and Querying Genomic Information. CIDR

Conference, Asilomar, CA.

Hernandez, Thomas and Kambhampati, Subbarao, 2004.

Integration of Biological Sources: Current Systems

and Challenges Ahead. ACM SIGMOD Record.

Jonquet, Clement, Musen, Mark A. and Shah, Nigam,

2008. A System for Ontology-Based Annotation of

Biomedical Data. DILS Workshop, Paris, France.

Karmakar, Samir, 2007. Designing Domain Ontology: A

Study in Lexical Semantics. Technical Report, Indian

Institute of Technology Kanpur, Kanpur, India.

Madhavan, Jayant, A. Bernstein, Philip and Rahm, Erhard,

2001. Generic Schema Matching with Cupid.

Microsoft Research (extended version of VLDB

Conference paper).

Melnik, Sergey, Garcia-Molina, Hector and Rahm, Erhard,

2002. Similarity Flooding: A Versatile Graph

Matching Algorithm and its Application to Schema

Matching. ICDE Conference, San Jose, CA.

Silva, Nuno and Rocha, Joa, 2003. “MAFRA-An

Ontology Mapping FRAmework for the Semantic

Web”.

International Conference on Business

Information Systems, USA.

Weeds, Julie and Weir, David, 2005. Co-occurrence

Retrieval: A Flexible Framework for Lexical

Distributional Similarity. MIT Press Journals.

Zhong, Jiwei, Zhu, Haiping, Li, Jianming and Yu, Yong,

2002. Conceptual Graph Matching for Semantic

Search. ICCS Conference, Borovets, Bulgaria.

ICEIS 2010 - 12th International Conference on Enterprise Information Systems

262