AN INCREMENTAL PROCESS MINING ALGORITHM
André Kalsing, Lucinéia Heloisa Thom and Cirano Iochpe
Institute of Informatics, Federal University of Rio Grande do Sul, Bento Gonçalves 91501-970, Porto Alegre, Brazil
Keywords: Process Mining, Workflow, Incremental Mining.
Abstract: A number of process mining algorithms have already been proposed to extract knowledge from application
execution logs. This knowledge includes the business process itself as well as business rules, and
organizational structure aspects, such as actors and roles. However, existent algorithms for extracting
business processes neither scale very well when using larger datasets, nor support incremental mining of
logs. Process mining can benefit from an incremental mining strategy especially when the information
system source code is logically complex, requiring a large dataset of logs in order for the mining algorithm
to discover and present its complete business process behavior. Incremental process mining can also pay off
when it is necessary to extract the complete business process model gradually by extracting partial models
in a first step and integrating them into a complete model in a final step. This paper presents an incremental
algorithm for mining business processes. The new algorithm enables the update as well as the enlargement,
and improvement of a partial process model as new log records are added to the log file. In this way,
processing time can be significantly reduced since only new event traces are processed rather than the
complete log data.
1 INTRODUCTION
Process mining aims extracting information from
system event logs to discovery a business process
based on its execution. Some examples of systems
include workflow management systems, enterprise
resource planning systems, customer relationship
management, B2B systems, legacy systems, etc.
This approach can also be used to compare both the
captured and the designed business process in order
to identify discrepancies in the model (van der Aalst,
2003).
Additionaly to process mining algorithms, there
are several other algorithms and methods for the
extraction of business processes from information
systems (e.g. Machine Learning, Source Code
Analysis, etc). Techniques based on static source
code analysis (Zou, 2006) (Zou, 2004), (Liu, 1999)
usually extract the business process directly from the
source code constructions (e.g. if and while
statements, functions calls, etc). Thus, the final
process model presents a similar structure as the
source code. The problem here is that they seldom
identify more complex constructions like parallelism
and process participants. The main reason for this
limitation is that this kind of information cannot be
gathered from the static analysis of the source code
alone, but needs a dynamic behavior analysis of the
system additionally. Existing process mining
algorithms (Ren, 2009), (Alves and Medeiros,
2007), (Weijters, 2006) extract information about
process behavior directly from system execution
logs (i.e. see Fig. 1). They can identify simple as
well complex control flow structures (e.g.,
XOR/AND-split/join, activitity participants) through
the dynamic behavior analysis of the system.
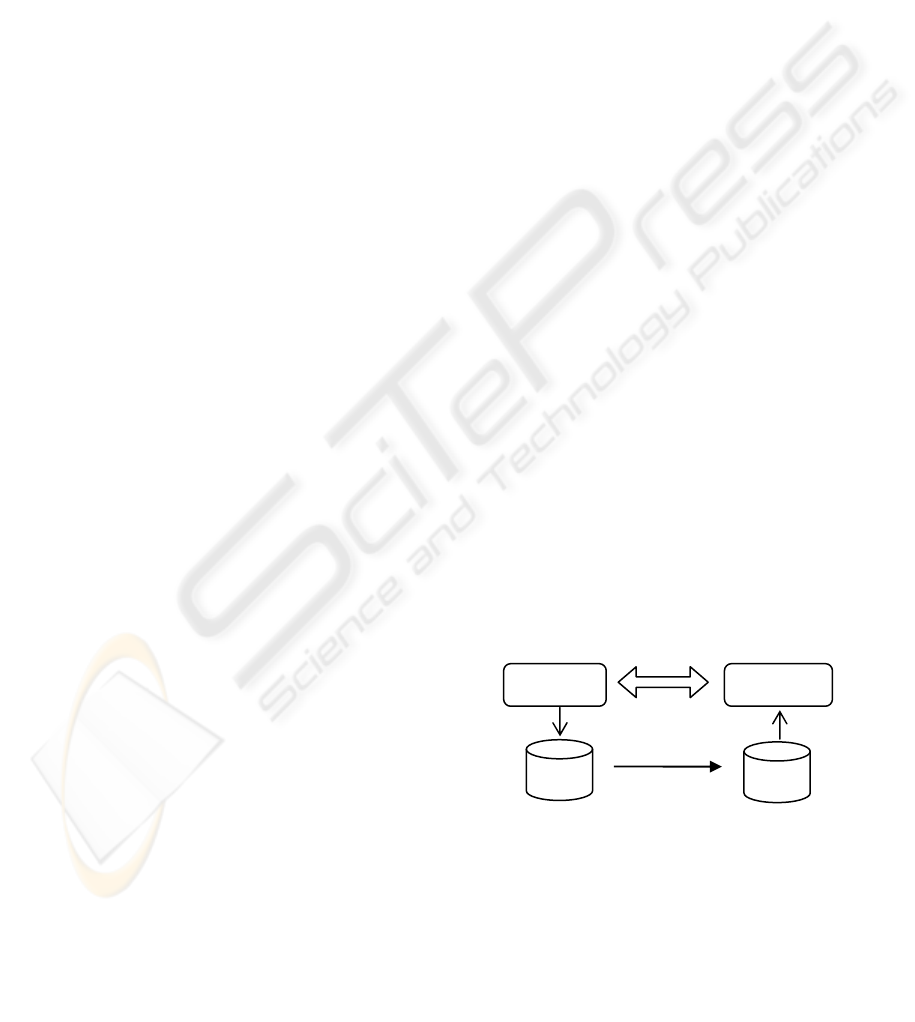
Figure 1: Overview of process mining.
Although actual process mining algorithms are
very effective for the extraction of business
processes, they still present some limitations. The
main limitations are (i) they do not scale very well
during the mining of large execution logs and (ii) do
not support the incremental mining of these logs.
Large log files might be necessary when a
Information
System
Process
Logs
records
events
Process Mining
Process
Models
supports/
controls
Operational
Processes
models
263
Kalsing A., Thom L. and Iochpe C. (2010).
AN INCREMENTAL PROCESS MINING ALGORITHM.
In Proceedings of the 12th International Conference on Enterprise Information Systems - Databases and Information Systems Integration, pages
263-268
DOI: 10.5220/0002906402630268
Copyright
c
SciTePress
significant number of different as well as complex
execution scenarios occur in the business process. In
such cases, the complete behavior of the system can
only be approximated by mining an ever growing
dataset of executions. So, in these cases an
incremental mining could extract partial results from
the log and also execute the mining process in a
more efficient way.
In this paper, we propose an incremental process
mining algorithm, the IncrementalMiner, as an
extension of the HeuristiMiner (Weijters, 2006) with
support to incremental mining of execution traces, as
showed in Fig 2 The main reason of relying upon the
HeuristicMiner in spite of other existing mining
algorithms, e.g., alpha++ (Wen, 2006) and Genetic
Miner (Alves de Medeiros, 2007), is basically its
satisfactory accuracy as well as its support in
extracting all business process constructions (e.g.,
XOR/AND-split/join, loops, activities participants,
etc).
Figure 2: Incremental Processs Mining from execution
logs of information systems.
The remainder of this paper is organized as
follows. Section 2 introduces basics concepts related
to process mining that are used throughout the paper.
Section 3 provides a detailed discussion on the
IncrementalMiner algorithm. In section 4, we
evaluate the performance of the new algorithm and
comment on the quality of the extracted models.
Section 5 we introduce the works related to this
research. Section 6 presents conclusions and
outlook.
2 BASIC CONCEPTS
An event log can be defined as follows. Let T be a
set of process activities.
T* is an event trace,
i.e., an arbitrary sequence of activity identifiers.
W
T* is an event log, i.e., a multiset (bag) of event
traces, where every event trace can appear many
times in a log.
To find a process model on the basis of an event
log, the log must be analyzed for causal
dependencies, e.g., if an activity is always followed
by another activity, it is likely that there is a
dependency relation between both activities. To
analyze these relations, Weijters (Weijters, 2006)
introduces the following notations. Let W be an
event log over T, i.e., W
T*. Let a, b T:
1)
wba
iff there is a trace
= t
1
t
2
t
3
…t
n
and i
{1, …, n-1} such that
W and t
i
=a and t
i+1
= b.
The relation
w in this notation describes which
activities apeared in sequence.
2) wba iff wba and b
w a. The relation
w
represents the direct dependency relation
derived from event log
W.
3) a║wb iff wba and wab . The relation ║w
suggest potencial parallelism between a and b.
4) a>>w b iff there is a trace
= t
1
t
2
t
3
…t
n
and i
{1, …, n-2} such that
W and t
i
= a and t
i+1
=
b and t
i+2
= a. This relation suggest a short loop
between
a and b.
3 ON THE INCREMENTAL
MINER ALGORITHM
IncrementalMiner incrementaly mines the control
flow perspective of a business process from
execution log files of this process. Incremental
mining happens when several partial event logs are
processed one by one improving the completeness of
model. Table 1 shows an example of two event logs.
The first one (Table 1a) contains the initial events
generated by the first execution of a system. Each
row in the table represents the events generated by
the execution of one process instance. The second
event log (Table 1b) contains additional and
complementary events generated by new executions
(i.e. the last row on Table 1b).
Table 1: Two complementary events log. * Interval of
instance Ids. ** Represent several identical event traces.
ID Trace
1-9 * A–C–B–D
9
*
*
10-19 A–E–D
10
20 A–B–C–E–D
1
21 A–E–C–B–D
1
ID Trace
1-9 A–C–B–D
9
10-19 A–E–D
10
20 A–B–C–E–D
1
21 A–E–C–B–D
1
22-30 A–B–C–D
9
(a) Partial log of event traces (b) Final log of event traces
3.1 Incremental Process Mining
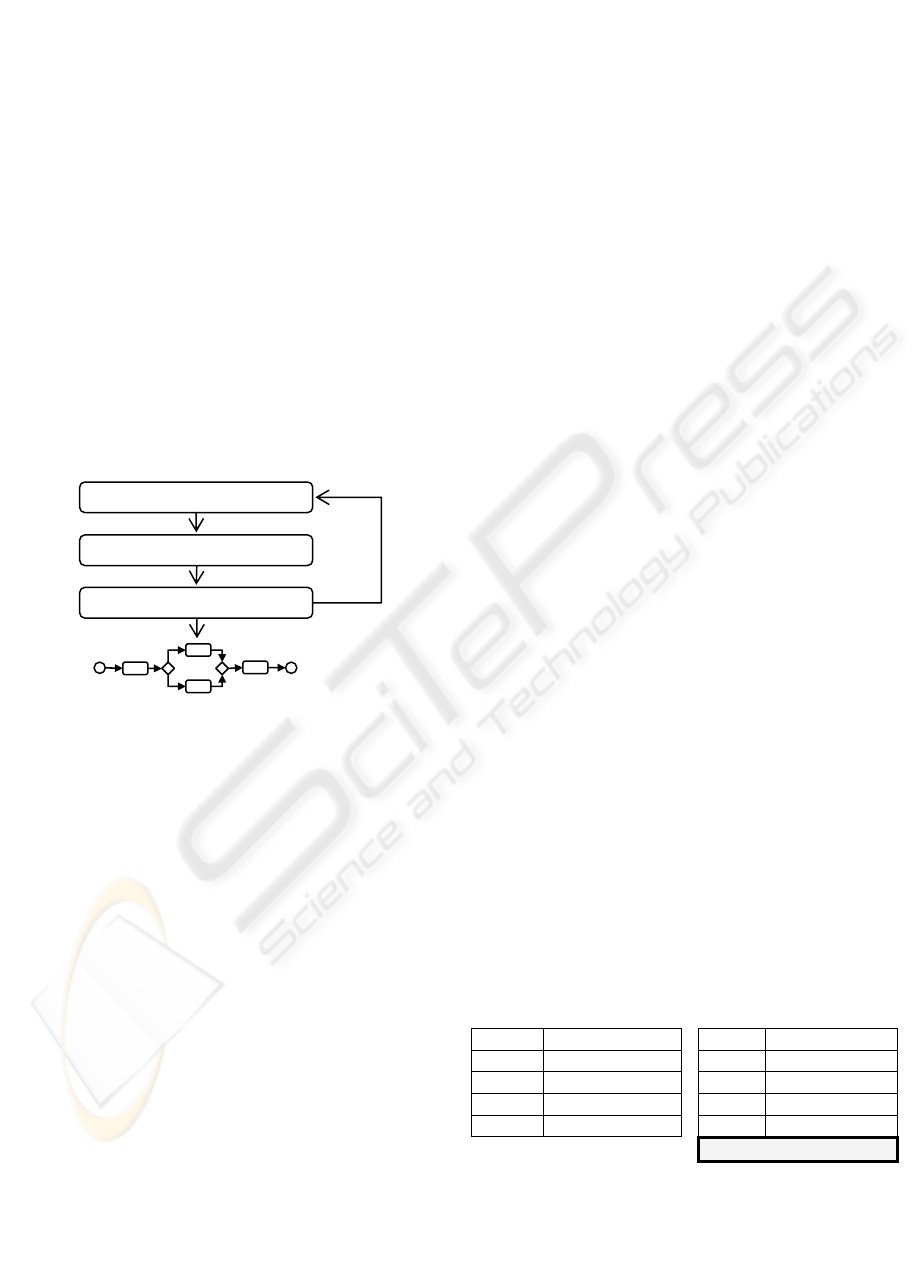
The process that incrementally generates the log
Define User Scenarios
(a)
(b)
(c)
(d)
Updated process model
Log entries generated
Test case scenarios created
Run Information System
Execute IncrementalMiner
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
264

starts with the definition of test case scenarios (i.e.
Fig. 2a). These scenarios coordinate which
funcionalities of the system are executed. As the
application is executed (i.e. Fig. 2b), new entries are
added to the log. The IncrementalMiner algorithm
can be executed at any time to handle these new
entries (i.e. Fig. 2c). As a result, it either creates a
new model (from scratch) at the first time, or it
updates already created process models at each time
it is executed (i.e. Fig 2d).
The incremental mining of logs allows more
flexibility to extract business process since only
specific processes could be selected, executed and
mined from the events log. So, this fact reduces the
total processing time of the mining since only new
trace entries are processed rather than the complete
log data when new processes must be considered.
3.2 The Algorithm Definition
This section gives an overview of the
IncrementalMiner algorithm. We separated the
algorithm in five distinct pseudo codes, as showed
below.
Algorithm 1: IncrementalMiner.
1. for every new instance
L
(a) for every event e
i
(i) e
1
= e
i
, e
2
= e
i+1
and e
3
= e
i+2
.
(ii) Process Relation(e
1
, e
2
, e
3
).
Algorithm 2: Process Relation (e
1
, e
2
, e
3
).
1. Create dependency relation rel(e
1,
e
2
).
2. Calculate confidence wba of rel(e
1,
e
2
).
3. If e
1
equal e
2
then
(a) Calculate short loop size 1 Confidence
waa between e
1
and e
2
.
(b) If the Support of rel(e
1,
e
2
) is above Loop1 threshold
then
(i) AddRelationToGraph(e
1
, e
2
).
4. Else If e
1
equal e
3
then
(a) Calculate short loop size 2 Confidence
wba 2
.
between e
1
and e
3.
(b) If support of rel(e
1,
e
3
) is above Loop2 threshold
then
(i) AddRelationToGraph(e
3
, e
1
).
5. Update rel(e
1,
e
2
) in the dependency tree of e
1
element .
6. Update split/join relation Confidence
cwba ^
for
e
1
, e
2
and e
3.
7.UpdateBestRelation(e
1,
e
2
, bestDependenciesTreeOf
(e
1
)).
8.UpdateBestRelation(e
1,
e
2
, bestCausesTreeOf (e
2
)).
9. If rel(e
1,
e
2
) is the best dependency relation of e
1
or
rel(e
1,
e
2
) is the best cause relation of e
2
or (Confidence
of rel(e
1,
e
2
) is above Dependency threshold and the
Support of rel(e
1,
e
2
) is above Positive Observation
threshold and confidence of rel(e
1,
e
2
) minus the
Confidence of best dependency relation associate to e
1
is above Relative to best threshold ) then
(a) AddRelationToGraph(e
1
, e
2
).
Algorithm 3: UpdateBestRelation(e
1,
e
2,
relationTree).
1. If Confidence of rel(e
1,
e
2
) is less than Confidence of
relations in relationTree then
(a) RemoveRelationFromGraph(e
1
, e
2
).
2. Else
(a) If Confidence of rel(e
1,
e
2
). is greater than relations
Confidence in relationTree then
(i) For each old best relation in relationTree:
(x) Remove old best relation from relationTree.
(y) RemoveRelationFromGraph(firstElementOf(
old best rel), secondElementOf(old best rel)).
(b) Add r to the relationTree.
Algorithm 4: AddRelationToGraph(e
1
, e
2
).
1. Add vertex(e
1
) and vertex(e
2
) to the dependency graph.
2. Add edge(e
1
, e
2
) to the dependency graph.
Algorithm 5: RemoveRelationFromGraph(e
1
, e
2
).
1. Remove edge(e
1
, e
2
) from dependency graph.
2. If vertex(e
1
) does not contains incoming and outgoing
edges then
(a) Remove vertex(e
1
) from dependency graph.
3. If vertex(e
2
) does not contains incoming and outgoing
edges then
(a) Remove vertex(e
2
) from dependency graph.
To exemplify how IncrementalMiner works,
consider the partial log W = {ACBD
9
, AED
10
,
ABCED
1
, AECBD
1
} (i.e. the log presented in the
Table 1a). For every three consecutive events in the
trace (e.g., events A, C, B in the trace ACBD), the
algorithm IncrementalMiner applies heuristics to
them to extract valid relations. The first heuristic to
be applied is the dependency relation (i.e. Algorithm
2, item 2) between the first and second element of
the triple (e.g. A and C). Let
W be an event log
on
T
, and Tba
, . Then || wba is the number
of times wba occurs in
W , and:
1||||
||||
wabwba
wabwba
wba
(1)
This above heuristic calculate the Partial
Confidence (i.e. the Confidence value until this
iteration of algorithm) of this relation, using the
support of
wba (e.g. number of times that A
comes before C) and the support of
wab
(e.g.
number of times that C comes before A). In the
example,
wba (1-0) / (1+0+1) = 0.5. After
iterating all log traces in our example, the value of
wba is (9-0) / (9+0+1) = 0.900. The calculated
values are inserted into the Dependency Tree of
Figure 3 (i.e. see node C, in the dependency tree of
A). This dependency tree is an AVL tree that keeps
the actual candidate relations (i.e. relations that
could be considered in the final graph of process)
together with their Confidence and Support values,
AN INCREMENTAL PROCESS MINING ALGORITHM
265
respectively. The next two heuristics below verify
the occurrence of short loops in the trace (item 3 of
Algorithm 2). That is, it checks the existence of an
iteration composed by either e
1
or e
1
and e
2.
(e.g. AA
or ABA). Let W be an event log over T, and a, b
T. Then |a >
W
a| is the number of times a >wa
occurs in W, and |a >>
W
b| is the number of times a
>>
W
b occurs in W:
||
||1
awa
awa
awa
(2)
||||
2
||||1
awb bwa
awb
awb bwa
(3)
The next heuristic (i.e. heuristic 4) is used by
algorithm 2 (i.e. item 6) to verify the occurrence of
non-observable activities in the log (i.e. AND/XOR-
split/join elements). Let W be an event log over T,
and a, b, c
T, and b and c are in depending
relation with a. Then:
||||
^
||||1
bwc cwb
awbc
awb awc
(4)
The |||| wcawba represent the number
of positive observations and
|||| wbcwcb
represent the number of times that b and c appear
directly after each other. Considering the event log
example, the value of
cwba ^
= (1 + 0) / (11 + 9
+ 1) = 0.05 indicates that E and C are in a XOR-
relation after activity A (i.e. high values to
cwba ^
indicates a possible AND-relation and
low values a XOR-relation).
All heuristics defined above are used to calculate
the candidate relations that can be added to the
dependency graph of the business process (i.e., the
best relations graph, represented in Fig. 5). To select
the candidate relations that will compose the graph,
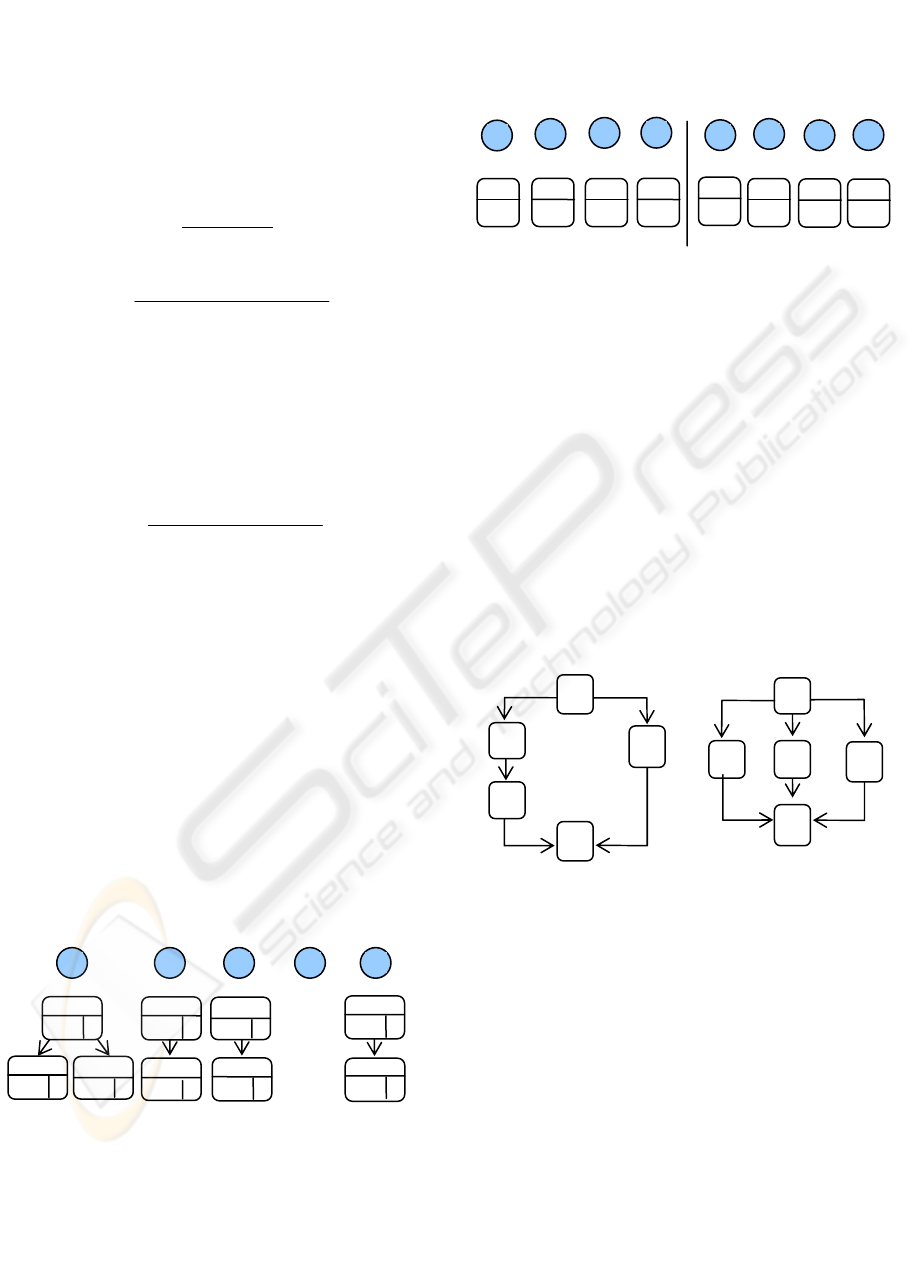
we use the best relations trees (see Fig. 4).
Figure 3: Dependencies trees. Keep the confidence and
support updated for every dependency relation.
The algorithm 3 is used to update these best
relation trees. These trees keep the best dependency
and causal relations of the dependency tree (i.e. the
relations with highest Confidence value). A best
relation tree can have several relations with high
confidence value inside it, but all relations in it must
have the same confidence value for that element.
Figure 4: Best relations trees. Best relations from
dependency tree of Fig. 3.
The final dependency graph is similar to the one
of Fig. 5a. We need yet to process the second log file
in its last state (see Table 1b). From this log file we
obtain the multiset W = {ACBD
9
, AED
10
, ABCED
1
,
AECBD
1
, ABCD
9
}. After applying IncrementalMiner
to this log, we obtain the final dependency graph of
Fig. 5b. This graph shows additional structures
which were extracted from the new trace ABCD (i.e.
nine occurrences of it) available in the last events of
the log. All the other traces available in the log (i.e.
also available in the first log) are discarded by the
algorithm. This happens since the IncrementalMiner
maintains a list of already processed event traces
(column ID in Table 1 can be used for this control).
Figure 5: Dependency graph example resultant from the
best relations of Fig 4.
3.3 Using Threshold to Deal with Noise
Additionaly to the best relations tree,
IncrementalMiner uses all thresholds defined in
HeuristicMiner algorithm to decide whether a
relation will be considered in the final dependency
graph (see items 3.(b), 4.(b) and 9 of Algorithm 2).
These thresholds help preventing the generation of
false relations caused by noise. Thus, we can also
accept dependency relations between activities that
have (i) a dependency measure above the value of
the Dependency threshold, and (ii) have a frequency
higher than the value of the Positive observations
0.900
0.916
0.909
0.916
0.750
A
E
B
C
D
0.909
0.909
0.900
0.909
0.916
0.900
A
E
B C
D
(b) Final dependency graph
From Table 1b
(a) Partial dependency graph
From Table 1a
A→E
A
B
C
(a) Best Dependency Trees
B
C
(b) Best Cause Trees
D
0.750
C
0.916
E
0.909
D
0.750
B
B→D
C→B
C→B
0.900
A
A→C
E→D
0.916
E
E
0.916
A
A→E
E
0.916
D
E→D
0.909 10
D
B C
0.750
10
B
A
0.500 1
B
0.900 9
C
0.916
11
E
0.0 1
E
-0.75 1
C
A→B
A→C A→E
B→D
B→C
C→E
C→B
D E
E→C
E→D
D
0.916
0.0 1
C
11
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
266
threshold, and (iii) have a dependency measure for
which the difference with the "best" dependency
measure is lower than the value of Relative to best
threshold (Weijters, 2006).
4 PERFORMANCE
EVALUATION THROUGH
A CASE STUDY
The experiments have been divided into two groups.
The first group compared the performance results
using the IncrementalMiner and other existent
algorithms. The second group was used to compare
the quality of models discovered by the process
mining algorithms.
4.1 Generating Event Log from Legacy
System Execution
For all experiments discussed here, we used datasets
generated through successive executions of an
information system, following the process defined in
Fig. 2. In the end, a large dataset with approximately
10,000 event trace instances were generated. In the
experiments we used a PC with an Intel Core 2 Duo
2GHz processor and 2GB RAM. The
IncrementalMiner algorithm was implemented using
Java language.
4.2 Performance Analysis
To test the performance of the incremental feature of
the IncrementalMiner, we collected five event trace
log files. The files were recorded with
complementary contents and named respectively as
A, B, C, D and E where (
.EDCBA
).
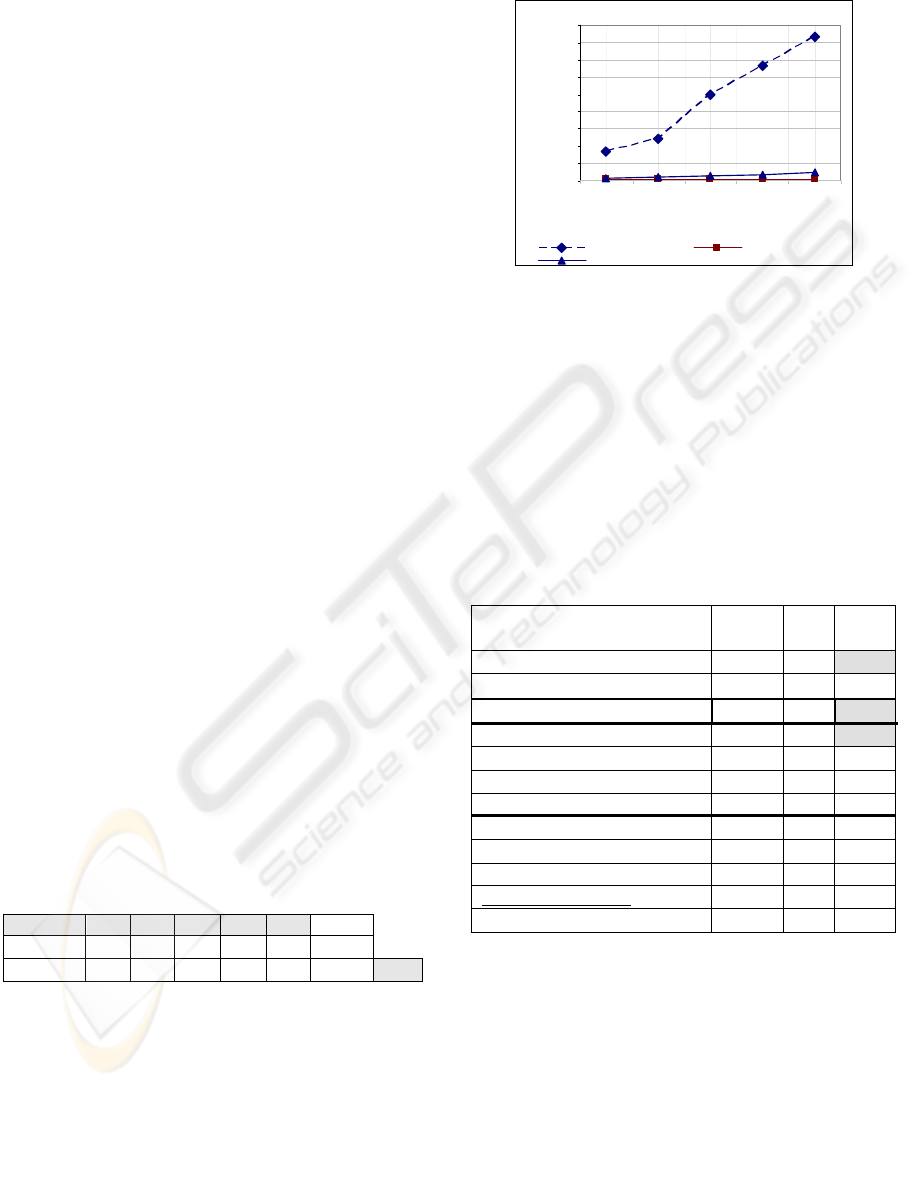
Table 2: IncrementalMiner time comparative (in seconds).
Row A: mining of all log content. Row B: incremental
mining of log content. * In thousands of instances.
Instances* 2 4 6 8 10
Total
A
1.4 2.7 4.0 5.4 6.7
20.2s
B
1.4 1.5 1.4 1.5 1.5
7.2s 64%
The obtained results can be seen in Fig. 6 below.
IncrementalMiner processed the complete dataset
five times faster (500%) than Alpha++ and eighty
times faster than HeuristicMiner (8000%).
Furthermore, Table 2 shows the total processing
time reduction with IncrementalMiner. Rows A and
B sum the total processing time to process the log
content without the incremental approach and with
it, respectively. At the end we obtained a gain of
64% on total processing time using incremental
mining of datasets.
Incremental M ining
0
25
50
75
10 0
12 5
15 0
17 5
200
225
2 +2 (4) +2 (6) +2 (8) +2 (10)
Incremental Transactions (x 1000 )
Run-time (Seconds)
HeuristicMiner IncrementalMiner
Al
p
ha++
Figura 6: Total processing time during the mining of new
transactions added to the log.
In our experiments we also considered the
execution time of the GeneticMiner algorithm
(Alves de Medeiros, 2007). However, this algorithm
has shown a total execution time even worse than
that of others algorithms presented in Figure 6.
4.3 Quality Analysis
Table 3: Quality Metrics Comparative between
IncrementalMiner (IM), HeuristicMiner (HM), Genetic
Miner (GM) and Alpha++ miner.
Metric IM/
HM
GM A+
+
Fitness Parsing Measure PM 1 1 0.006
Token Based Fitness (f)
1 1 0.926
Fitness PF
com
p
lete
1 1 0.728
Behavioral Appropriateness a’
B
0.78 0.98 0.720
Behavioral Precision Bp 1 1 0.907
Behavioral Recall Br 1 1 0.907
Causal Footprint 0.99
1
0.96
Structural Appropriateness a’
S
1 1 1
Structural Precision S
P
1 1 1
Structural Recall S
R
1 1 1
Duplicates Precision D
P
1 1 1
Duplicates Recall D
R
1 1 1
This quality comparison followed the quality metrics
defined in (Rozinat, 2007a). Such metrics describe
several measurements to assess the quality of a
model based on the behavior observed in the
execution log. According to Rozinat (Rozinat,
2007a), a value can be considered a “good metric” if
it is near or equal to “1”.
To execute these experiments, we have used the
Control Flow Benchmark plug-in of the ProM tool
(van Dongen, 2005b). Table 3 presents the result of
this analysis. We observed that all discovered
AN INCREMENTAL PROCESS MINING ALGORITHM
267

models except the models returned by Alpha++
miner fit the log and have good precision. The
details of each metric can be seen in the work of
Rozinat.
5 RELATED WORK
The first group of related work includes process
mining algorithms. They allow the mining of
execution traces of a system to extract information,
as business processes, aspects of organizational
structures and types of business rules (van der Aalst,
2003). Related to that, one of the main algorithms is
the Genetic Miner. It uses adaptive search methods
that simulate the evolution process. This algorithm
presents better accuracy when compared with other
existing ones (e.g., Petrify Miner, Alpha++, etc).
However, existent algorithms do not consider the
incremental mining of business process from the
event log, using only historical data logs.
The source code analysis approach proposed in
(Zou, 2004) represents a model driven business
process recovery framework that captures the
essential functional features represented as a
business process. In another work, Zou (Zou, 2006)
compares the structural features of the designed
workflow with the implemented workflow, using an
intermediate behavioral model. Finally, Liu (Liu,
1999) uses a requirements recovery approach which
relies on three basic steps: 1) Behavior capturing; 2)
Dynamic behavior modeling; and 3) Requirements
derivation as formal documents. All these
approaches use only static information to extract
business process models from information systems.
6 SUMMARY AND OUTLOOK
This paper proposed the IncrementalMiner, an incre-
mental process mining algorithm for the extraction
of business processes models from information
system event log. The algorithm is an extension of
the HeuristicMiner where the data structure used
was restructured in order to support the incremental
update of the model. In its performance evaluation,
the total processing time of logs was reduced in 64%
during the incremental mining and was five times
faster than Alpha++ and eighty times faster than
HeuristicMiner. The extracted process models
showed good accuracy when compared with results
of other process mining algorithms.
Altogether, the main contribution of this work is
the incremental functionality of the algorithm to
support incremental learning of business processes
models by processing event trace logs that are
recorded during successive system executions.
In the near future, we intend to do additional
performance and quality tests with
IncrementalMiner to consider other types of
processes and datasets.
REFERENCES
Alves de Medeiros, A. K., Weijters, A. J. M. M., van der
Aalst, W.M.P., 2007. Genetic Process Miner: An
Experimental Evaluation. Data Mining Knowledge
Discovery. V.14(2). pp. 245-304. Springer.
Liu, K., Alderson, A., Qureshi, Z. 1999. Requirements
recovery from legacy systems by analysing and
modelling behaviour. Proceedings of the International
Conference on Software Maintenance, pp. 3-12
Ren, C., Wen, L., Dong, J., Ding, H., Wang, W, Qiu, M.,
2009. A Novel Approach for Process Mining Based on
Event Types. Journal of Intelligent Information
Systems, Vol. 32(2). pp: 163-190. Springer.
Rozinat, A., Alves de Medeiros, A. K., Gunter, C. W.,
Weijters, A. J. M. M., van der Aalst, W. M. P., 2007a.
Towards an Evaluation Framework for Process
Mining Algorithms. BPM Center Report BPM-07-06.
van der Aalst, W. M. P., van Dongen, B. F., Herbst, J.,
Maruster, L., Schimm, G., Weijters, A. J. M. M. 2003.
Workflow mining - A survey of issues and approaches.
DKE, Vol. 47(2). pp: 237-267. Elsevier.
van Dongen, B. F., Alves de Medeiros, A. K., Verbeek,.H.
M. W., Weijters, A. J. M. M., van der Aalst, W.M.P.,
2005a. The ProM framework - A new era in process
mining tool support. Application and Theory of Petri
Nets. Vol. 3536. pp: 444-454. Springer
Weijters, A. J. M. M., van der Aalst, W. M. P., Alves de
Medeiros, A. K., 2006. Process Mining with the
HeuristicMiner Algorithm. Technische Universiteit
Eindhoven, Tech. Rep. Vol. 166.
Wen, L., Wang J., Sun J. G., 2006. Detecting Implicit
Dependencies Between Tasks from Event Logs. In
Asia-Pacific Web Conference on Frontiers of WWW
Research and Development (APWeb 2006), Lecture
Notes in Computer Science, pp: 591–603. Springer.
Zou, Y., Hung, M., 2006. An Approach for Extracting
Workflows from E-Commerce Applications.
Proceedings of the 14th IEEE International
Conference on Program Comprehension, pp. 127 –
136.
Zou, Y., Lau, T. C., Kontogiannis, K., Tong, T.,
McKegney, R., 2004. Model-driven business process
recovery, 11th Working Conference on Reverse
Engineering, IEEE Computer Society Washington,
DC, USA. pp 224- 233.
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
268
