A THREE LEVEL ABSTRACTION HIERARCHY
TO REPRESENT PRODUCT STRUCTURAL INFORMATION
Marcela Vegetti, Horacio Leone
Instituto de Desarrollo y Diseño(INGAR), Avellaneda 3657, Santa Fe, Argentina
Gabriela P. Henning
INTEC (Universidad Nacional del Litoral, CONICET), Güemes 3450, Santa Fe, Argentina
Keywords: Product Model, Ontology, BOM.
Abstract: Product models should integrate and efficiently manage all the information associated with products in the
context of industrial enterprises or supply chains (SCs). Nowadays, it is quite common for an organization
and even, each area within a company, to have its own product model. This situation leads to information
duplication and its associated problems. In addition, traditional product models do not properly handle the
high number of variants managed in today competitive markets. Therefore, there is a need for an integrated
product model to be shared by the organizations participating in global SCs or all areas within a company.
One way to reach an intelligent integration among product models is by means of an ontology. PRONTO
(PRoduct ONTOlogy) is an ontology for the Product Modelling domain, able to efficiently handle product
variants. This contribution presents a ConceptBase formalization of PRONTO, as well as an extension of it
that allows the inference of product structural knowledge and the specification of valid products.
1 INTRODUCTION
Within an organization, many management and
production functions make use of product structural
data in different manners depending on their
requirements. Thus, such information is represented
in formats that best meet the needs and business
processes of the various organizational areas. In
addition, traditional product models do not properly
handle the high number of variants that characterize
today competitive markets. These situations lead to
the presence of redundant and possibly inconsistent
product information. Moreover, all the planning,
coordination and support functions, required for
carrying out manufacturing and logistic activities,
demand accurate and reliable product information of
different granularities in order to be efficient.
Circumstances get worse when organizational
units not only use product data for their own needs
but also exchange it with other partners, e.g. during
cooperative product development, when outsourcing
manufacturing activities, interacting with logistics
providers, etc. In all these cases the use of different
product models can lead to semantic problems.
In the last decade ontologies have been
recognized as key elements to reach semantic
integration, since they provide formal models that
establish a consensual and precise meaning to the
information communicated among different sources.
In previous works (Giménez et al., 2008; Giménez et
al. 2009), an ontology named PRONTO (PRoduct
ONTOlogy) was presented. This ontology integrates
two hierarchies to represent product information: the
Abstraction Hierarchy (AH) and the Structural one
(SH). However, these contributions were limited to
the representation of explicit data at each level of the
AH.
This paper presents a ConceptBase (Jarke et al.,
2004) formal specification of PRONTO that focuses
on the structural hierarchy of the ontology and in the
way structural information can be inferred from
explicit knowledge at each AH level. This proposal
efficiently handles a great number of variants and
allows representing product information with
distinct granularity degrees, useful for planning
activities taking place at different time horizons.
Additionally, constraints associated with the
specification of valid products are introduced in the
299
Vegetti M., Leone H. and P. Henning G. (2010).
A THREE LEVEL ABSTRACTION HIERARCHY TO REPRESENT PRODUCT STRUCTURAL INFORMATION.
In Proceedings of the 12th International Conference on Enterprise Information Systems - Artificial Intelligence and Decision Support Systems, pages
299-308
DOI: 10.5220/0002907102990308
Copyright
c
 SciTePress

ontology. Section 2 briefly introduces PRONTO
concepts, describes its formalization, presents how
implicit knowledge can be inferred from the explicit
one. Section 3 illustrates the use of the implemented
ontology by means of a case study. Finally,
conclusions are drawn.
2 PRONTO SPECIFICATION
Within the scope of this contribution, a product is a
complex concept (indeed much more complex than a
mere thing or substance produced by a natural or
industrial process) that will be defined at different
levels of abstraction. The term ProductAbstraction is
used to represent such complex thing.
In order to manage the complexities of product
information, two model hierarchies are included in
PRONTO: the Abstraction Hierarchy (AH) and the
Structural Hierarchy (SH) (see Fig. 1). The first one
represents the product concept at three abstraction
levels: Family, VariantSet and Product. The
Structural Hierarchy organizes the knowledge
related to product structural information. The SH is a
mechanism to manage the information associated
with the multiple recipes and/or processes available
to manufacture a given product or a group of similar
products. Within this hierarchy, a piece of
information that is typically handled is the Bill of
Materials (BOM) representation.
PRONTO allows representing BOMs of products
that are obtained by assembling component parts, as
well as others that are obtained by the
decomposition of non-atomic raw materials. Hence,
the SH considers two types of hierarchies, one which
relates a product with its component parts and
another one which associates a product with its
derivative parts. The relationships that are used to
represent each of these types are named component
Of and derivativeOf, respectively. As shown in Fig.
1, both relations are a specialization of the
SHRelation class, which links a ProductAbstraction
instance (whole) with zero or more
ProductAbstraction instances (part), which are
defined at the same abstraction level.
The Abstraction Hierarchy (AH) shown in Fig. 1,
is oriented towards managing the complexity that
results from the huge number of products that are
manufactured by current industrial facilities. It
includes the following abstraction levels:
Figure 1: Abstraction and Structural hierarchies.
 Family: It is the highest level of abstraction and
represents a set of similar products. They can
share one or more common structures. Such
structures can be specialized in the following
abstraction level of the hierarchy.
 VariantSet: It is the second level and models a
subset of Family members that share the same
structure and/or similar characteristics; i.e. a
subfamily. The structure of a VariantSet can
include modifications in the structure of the
family of which it is associated.
 Product: It corresponds to the lowest level in the
AH. It represents individual items (real products)
that are members of a particular VariantSet.
Therefore, each product has the structure that is
associated with the VariantSet of which it is a
member.
The proposed ontology has been formally
specified in the O-Telos language, which combines
object-oriented principles with first order logic
properties. It has been implemented in ConceptBase
(Jarke et al., 2004), a deductive object-oriented data
base manager. ConceptBase integrates techniques
from deductive and object oriented databases in the
logical framework of the O-Telos data model, a
dialect of Telos.
Fig. 2 shows how the ProductAbstraction class
and its subclasses are expressed in ConceptBase.
The specification also presents the constraints that
the memberOf relationship (attribute memberOf, in
Fig. 2) has to satisfy. This constraint establishes that
entities belonging to the two lower levels of the AH
are related to just one entity defined at their
immediate upper level through the memberOf
relationship (memberOf_necessary constraint) and
such relation is unique for each instance of the lower
level (memberOf_single constraint).
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
300

Figure 2: ProductAbstraction class and its subclasses.
Fig. 3 presents the complete conceptual model of
the ontology with the main concepts of each
abstraction level.
The Abstraction Hierarchy is related to the
Structural one by means of the SHRelation. As it
was previously mentioned, the componentOf and
derivativeOf relations define the two possible
structural associations among entities belonging to
the same abstraction level (Fig. 2). Both relations,
which define the SH, are not explicitly represented
in the conceptual model of Fig. 3, but they can be
inferred from the explicit information that is
recorded at each level of the AH.
Figure 3: PRONTO concepts.
Fig. 4 illustrates, by means of an example, the
SH that can be computed at each abstraction
hierarchy level. The first part of this figure shows
the abstraction hierarchies of three product families:
A (having 4 members: Avs1, Avs2, Avs3 and Avs4),
B (having 2 members) and C (having 3 members).
Fig. 4 also shows that the variant set Avs1 has
products Avs11 and Avs12 as members. Part 2 of this
figure presents the structural hierarchy of family A,
which has families B and C as its components.
Finally, parts 3 and 4 of Fig. 4 show a partial view
of the structural hierarchies that can be inferred at
the variant set and product levels, respectively.
2.1 Family Level Concepts
PRONTO prescribes that a family (Family) may be
composite (CFamily) or simple (SFamily),
depending on whether it represents a product having
or not a structure. A product has a structure when it
is made out of other products or other products can
be derived from it. In order to be a CFamily, it is
necessary to define a structureOf relation between
such family and at least one structure (this constraint
is specified at the beginning of Fig. 5). If more than
one structure is defined for a given CFamily, the
alternative structures of such family are linked by
the alternativeStructure relationship. As Fig. 5
shows, the values of the alternativeStructure
attributes are computed by the AltStrRule deductive
rule of the Structure class.
A CFamily represents a set of similar products
and, as already mentioned, such products could be
obtained by the assembly of others or by the
disaggregation or decomposition of non-atomic raw
materials. Therefore, the Structure class has been
specialized to represent these different types of
structures by means of the CStructure and
DStructure subclasses which, in turn are related to
the components or the derivatives of a family by
means of the CRelation and DRelation classes,
respectively. Both classes are specializations of the
Relation one. Each of them contains, at least,
information about: (i) the quantity/number of a
given component needed to manufacture a unit of
product (CRelation) or the quantity/number of
intermediate units obtained from the decomposition
of a unit of non-atomic raw material (DRelation);
and (ii) the proportion that a given component
represents in one unit of the product in whose
structure such component participates (CRelation) or
the yield that a given intermediate product renders
from the decomposition of a unit of a non-atomic
raw material (DRelation); (iii) minimum and
maximum allowed quantities and the quantities’ unit
of measure; as well as (iv) the relation type.
Besides, different kinds of relations are specified
to capture the rules needed to incorporate a certain
component (derivative) in a particular product
structure: (i) Mandatory: the component
(derivative) MUST be present in the structure of all
A THREE LEVEL ABSTRACTION HIERARCHY TO REPRESENT PRODUCT STRUCTURAL INFORMATION
301

Figure 4: Inferred structural hierarchies at each level of the AH.
the family members; (ii) Optional: the component
(derivative) CAN PARTICIPATE OR NOT in a
particular product structure; and (iii) Selective: the
component (derivative) should be selected from a set
of components, but ONLY ONE member of such set
(see selectedSet attribute and selSetRule rule of the
SelectiveRel class in Fig. 5) must be part of the
structure. Fig. 3 shows that such classification is
represented in the model with the isClassifiedAs
relation, the RelationType class and its subclasses
(OptionalRel, MandaroryRel and SelectiveRel). The
formal specification of these concepts is shown in
Fig. 5.
Due to the fact that the structure is explicitly
defined at the Family level, it is straightforward to
infer the SHRelations among the entities belonging
to this level. The composition relations (CRelation)
identify the components of a composite structure
CStructure, while the decomposition relations
(DRelation) do the same with the derivatives of a
DStructure. The definition of the deductive rule
(compRule) that infers the values of the component
attribute of a CFamily is specified in Part 1 of Fig.6.
In turn, the specifications of compRule
corresponding to the other two levels, CVariantSet
and CProduct, are shown in Parts 2 and 3 of Fig. 6.
Figure 5: Formalization of Family level concepts.
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
302

Figure 6: Examples of deductive rules that compute the components of the structural hierarchies at different AH levels.
2.2 Variant Set Level Concepts
At the Variant Set level, the structural hierarchy of
an entity depends on the structure of the family from
which such entity is a memberof. A VariantSet may
have the same structure of its family or may
introduce some modifications on it. CFamily
members having a similar structure are clustered
within the composite variant set concept
(CVariantSet in Fig.3). In the ontology model, a
CVariantSet instance is linked with one and only
one of the structures of its family by means of the
“has” relation. Fig. 7 presents a partial view of the
specification of the variant set level concepts.
The ChangeSet class groups all the changes that
are applied to the family structure in order to obtain
the particular structure of a composite variant set.
Each specified change (Change class) affects only
one relation of such structure, which is pointed out
by the affectedRelation association of the Change
class, presented in Fig. 7. The Change class is
specialized into the QuantityChange, Family
Removal and FamilySpecification subclasses to
represent the different types of modifications
considered in the model. They represent (i) a value
change of the quantity per unit (quantity PerUnitCh)
or production factor (productionFactorCh)
attributes; (ii) the elimination of a component; or
(iii) the choice of one association that belongs to the
set of the SelectiveRelations of the modified
structure.
Applying the different types of modifications to
a structure depends on the type of the affected
relation. The first type of change is acceptable for all
relation types. However, removing a relation from a
structure requires such relation to be an optional one,
while the last type of change is only valid for
relations being of selective type.
Figure 7: Formalization of some Variant Set level
concepts.
As it was previously mentioned, Fig. 3, Part 3,
presents all the structural hierarchies that can be
computed for Avs1, which is one of the variant set
members of A. The total number of SHs of Avs1 is
obtained by multiplying the number of B members
(#B) by the number of C members (#C). Sometimes,
not all the SHs of a variant set are valid. Let us
assume, for example, that for commercial reasons
the products that are members of Avs1 must be
manufactured by using only products that are
members of the Bvs1 variant set. In such a case, only
three of the SHs that are shown in Fig. 3 Part 3 are
A THREE LEVEL ABSTRACTION HIERARCHY TO REPRESENT PRODUCT STRUCTURAL INFORMATION
303

valid (those that have Bvs1 as a component). In
order to represent this restriction, the model resorts
to the AllowableVariantSet class, which links a
variant set with the variant sets that are compulsory
to be used in its associated structural hierarchies. In
the case of the aforementioned example, an instance
of AllowableVariantSet has to be defined indicating
that Bvs1 is the allowable variant set of Avs1.
Part 2 of Fig 6 shows the deductive rule that was
defined to infer the components of a variant set. A
variant set vs2 is a component of another variant set
vs1 if:
 There exists an instance of the Allowable
VariantSet a1 in vs1 that has vs2 as a restricted
Set (compRule); or
 vs2 is a memberOf a family f2, which is
component of a family f1 from which vs1 is a
member of. Besides, no restriction applies to the
members of f2 defined in vs1 (restrictsMember
property) and the relation that specifies f2 as a
component is not eliminated from the structure
of vs1 (compRrule2).
2.3 Product Level Concepts
The most concrete level of the proposed Abstraction
Hierarchy represents real products that are members
of a VariantSet. Such membership relation is
represented by the memberOf link between the
VariantSet and the Product classes (specified in Fig.
2). A Product can be simple (SProduct) or
composite (CProduct) depending on whether it is a
member of SVariantSet or CVariantSet, respectively.
The instances of the CProduct subclass are members
of the corresponding CVariantSet instances and
represent non-atomic products; that is, products
having a structure. The variant set to which a
product belongs determines and restricts its SH. In
order to identify which product member is the one
that participates in the structural hierarchy of a
specific product, the chosenProduct relation is
employed (Fig. 3).
At the variant set level, all the components
(derivatives) included in the structural hierarchies
are instances of the VariantSet class. At the product
level, the entities included in a SH must be products
that are memberOf components (derivatives)
participating in the corresponding SH defined at the
variant set level. The deductive rule (compRule) that
is shown in Part 3 of Fig. 6 establishes that a product
p2 is a component of a product p1 if it is member of
a variant set cv2 that, in turn, is a component of the
variant set from which p1 is a member of.
Structural hierarchies at the product level can be
computed for each SH defined at the variant set
level. It should be noted that the model does not
explicitly represent all the potential SHs at the
product level. It is possible to calculate the explicit
product structural hierarchies that are required at a
given time; e.g., when receiving a production order
from a customer.
2.4 Material Requirements Inference
Product structural information is necessary to build
the Production Master Plan, which determines the
amounts of raw materials and intermediate products
that need to be purchased or manufactured in order
to fulfill a given final product demand. Therefore, as
important as the inferred information about
components and derivatives of a final product are
the quantities of materials that are required to
manufacture a certain amount of it.
One of the main contributions of the product
model is its ability to capture the manufacturing
composition and decomposition structures of
products. As shown, the ontology employs two
different types of structures (CStructure and
DStructure) with two types of relations (CRelation
and DRelation) to represent this information. Also,
each type of structure computes in a different way
data needed about manufacturing requirements of
raw materials and/or intermediate products. Fig. 8
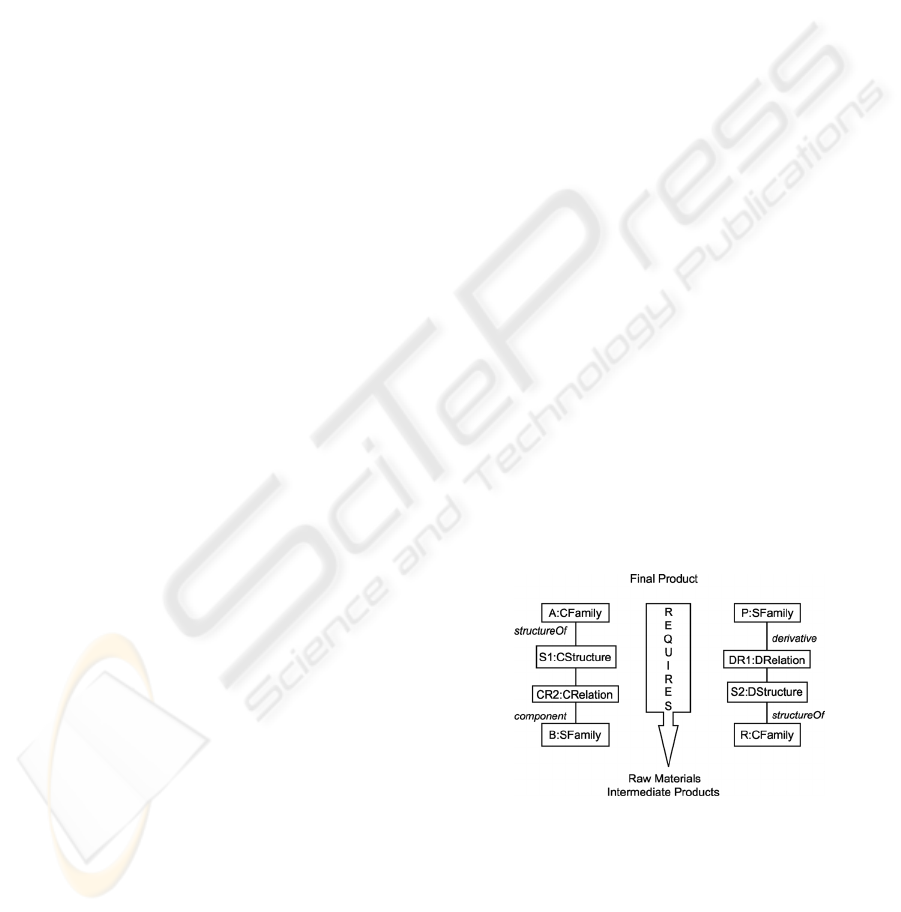
shows two families, representing final products A
and P. The former is obtained by assembling a set of
raw materials and intermediate products. The latter
is a derivative of a non-atomic raw material R.
Figure 8: Conceptual representation of the computation
of manufacturing product requirements.
For composition structures, the families that are
required to manufacture the composite family A (by
means of the S1 CStructure) match with the values
of the component attribute of the CRelation
associated with such structure (CR2).
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
304

For decomposition structures, the required
families have to be inferred in the inverse direction;
that is, starting from family P, it is necessary to
obtain the decomposition relation for which P is the
value of the derivative attribute (DR1), then, find the
decomposition structure in which this relation is part
of (S2) and, finally, from such structure the required
family R can be found. In order to implement these
mechanisms, the capabilities of Concept Base views
have been chosen. A ConceptBase view allows
presenting information of instances of a specific
class in a particular manner and defining attributes
whose values can be computed by means of
deductive rules. Such values can also be generic
views which can be particularized by assigning
values to parameters defined in the generic view. In
this PRONTO implementation, specific views were
defined in order to calculate the material
requirements of the different types of Product
Abstractions. In particular, the FamilyReq view
computes requirements at the family level and the
results of its execution are presented in Section 3.
2.5 Product Constraints Concepts
In this proposal, as in other approaches that are
based on the generic structure concept of a product
family, rules are used to properly specialize
structures into particular ones. In general, a great
number of possible component (derivative)
combinations are allowed (e.g. see the partial view
shown at the bottom of Fig. 4). However, some of
these combinations can be invalid due to technical or
commercial reasons. Generic product structures
defined at the Family and VariantSet levels include
an implicit product structure model, which provides
additional conditions that must be satisfied by a
valid product instance (Mänisto et al, 1998). In order
to obtain valid particular structures from generic
ones, it is necessary to have a methodology to: (i)
specify constraints among components (families,
variant sets or products) and, (ii) test the satisfaction
of such rules when generating more specific
(particular) structures. Based on these requirements,
the proposed model includes mechanisms to express
constraints which have to be fulfilled when creating
new particular or generic structures.
The proposal includes three types of restrictions,
according to the three abstraction hierarchy levels. It
is possible to define constraints among: (i) families
(FRestriction); (ii) variant sets (VSRestriction); and
(iii) products (PRestriction). Fig. 9 shows the classes
that represent such concepts, which are formalized
in Fig. 10. The specialization in FRestriction,
VSRestriction and PRestriction subclasses limits the
definition of constraints among entities of the same
AH level.
Figure 9: Product constraints concepts.
Fig. 10 shows that the restricts attribute has
different values in each Restriction subclass of the
AH. Similarly, the type of the hasRestriction
attribute is limited to have the FRestricion,
VSRestriction and PRestriction values in the Family,
VariantSet and Product classes, respectively
Figure 10: ConceptBase implementation of product
constraints concepts.
At any AH level it is possible to identify two
main types of restrictions among components: (i)
Obligatory and (ii) Incompatible; both must be
satisfied to obtain valid structures. Fig. 9 and 10
show that a Restriction is linked with its type by the
isClassifiedAs association and that the Mandatory
Const and IncompatibleConst classes represent the
constraint types defined in the model. The first type
forces a given component (family, variant set or
A THREE LEVEL ABSTRACTION HIERARCHY TO REPRESENT PRODUCT STRUCTURAL INFORMATION
305

product) to participate at any level of the SH of the
ProductAbstraction instance that specifies the
mandatory constraint. In contrast, incompatible
restrictions require a given component (family,
variant set or product) to be not present at any level
of the SH of the ProductAbstraction instance that
specifies such constraint. Both types of constraints
must be fulfilled in order to obtain valid structures.
Constraints defined in the previous paragraph are
to be tested for any pair of components (derivatives)
located at any SH level. Since the componentOf
(derivativeOf) relations are just defined for adjacent
levels, they need to be extended to consider multiple
levels of the SH. So, the mlComponentOf and
mlDerivativeOf attributes, and their corresponding
deductive rules, are defined for the Family, Variant
Set and Product classes. Such attributes allow
identifying whether a given product abstraction
participates at any level of the SH of another product
abstraction. Fig. 11 shows an example of ml
ComponentOf and its corresponding deductive rule
for the Family class. Thus, a family f2 is a multi
level component of f1 if f2 is direct component of f1
or there exists another family f3,
which is component
of f1, and f2 family is mlComponentOf f3.
Figure 11: Attributes and constraints added to test
restriction compliance.
Additionally, some integrity constraints have to be
defined in the Restriction class in order to ensure
restriction compliance. Two of such constraints are
presented in Fig. 11 as attributes of the Restriction
class. The first one, named MandConst, specifies
that the existence of a mandatory type of restriction
between two product abstractions (pa1 and pa2)
requires pa2 to be a multilevel component of pa1.
The other one, named IncompConst, which
prescribes an incompatibility restriction between pa1
and pa2, implies pa2 not to be a multilevel
component of pa1.
3 CASE STUDY
The meat industry was chosen to test the PRONTO
implementation presented in this paper. This
industry produces large quantities of a wide range of
products. Each product is sold in different packages,
depending on the market. Besides, a given cut is
considered a distinct product depending on the
quality of the steer from which it was obtained.
Therefore, the number of products variants handled
by this industry is very high. In addition, meat
products have complex hybrid composition/
decomposition structures. Raw materials are non
atomic, i.e., a sequence of decomposition operations
is needed to obtain intermediate products which are
later transformed into finals ones by manufacturing
processes. In addition, decomposition operations can
be made in different ways, so distinct products may
be obtained from a unique intermediate product.
The example presented in this section (due to
lack of space, just a test case partial view) focuses
on the representation of intermediate products,
which, together with packaging materials, participate
in the production of frozen cooked beef final
products. The AH that was defined for the products
considered in the example is shown in Table 1.
Table 1: Abstraction Hierarchy of an example product.
Family Variant Set Product
Frozen
Cooked
Beef
CookedBeefforDicing (CBD)
CBD1
CBD2
CBD4
SeasonedCookedBeef (SCB)
SCB3
SCB5
GroundCookedBeef (GCB)
GCB6
GCB7
GCB2
Fig. 11 presents the FrozenCookedBeef family,
its structures and the relationships of one of them.
FrozenCookedBeefSTR is a composition structure
(CStructure) that is defined by four composition
relations: R12, R13, R14a and R14b. Fig. 12 also
shows that Salt, Gelatin, CookedBeefRM3 and
CookedBeefRM2 correspond to the values of the part
attribute of the above relations. In the same way,
1754KG, 15KG and 12KG are the values of the
quantityPerUnit attribute corresponding to each
component.
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
306

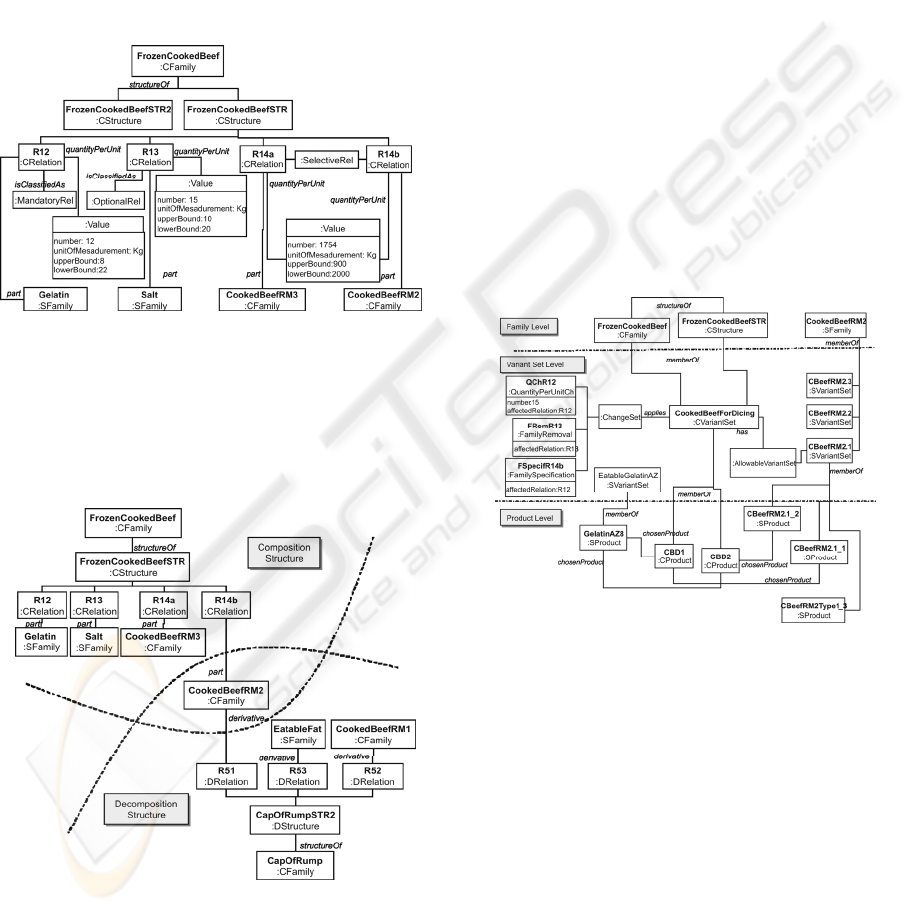
Fig. 12 also shows that R12 is a mandatory
relation, while R13 is an optional one. R14a and
R14b are selective relations, which imply that only
one of them has to be present in the structure of a
particular product. Thus, two structural hierarchies
are implicit in the definition of the Frozen
CookedBeefSTR: (i) one that comprises 12KG of
Gelatin (R12), 15KG of Salt (R13) and 1754 KG of
CookedBeefRM3 (R14a); (ii) and another one
composed of 12KG of Gelatin (R12), 15KG of Salt
(R13) and 1754KG of CookedBeefRM2 (R14b).
Figure 12: FrozeenCookedBeef family.
It is also possible to see in Fig. 13 that the
CookedBeefRM2 family participates in two different
structures: as a derivative in the decomposition
structure of the CapOfRump family and also as a
component of the FrozenCookedBeef one.
Figure 13: CookedBeefRM2 participating in composition
and decomposition structures.
To exemplify the definition of a variant set, Fig.
14 illustrates the representation of CookedBeefFor
Dicing, which is member of FrozenCookedBeef
family and has FrozenCookedBeefSTR as its
structure. Also, Fig. 14 shows that the CookedBeef
ForDicing variant set introduces three changes into
the family structure. The figure also depicts
elements of the variant set and product levels. The
middle part of it illustrates how an instance of
AllowableVariant Set relates to CookedBeefFor
Dicing. Such instance specifies the CookedBeef
RM2.1 variant set as one of the components of the
possible SHs of the variant set being defined. The
bottom part of Fig. 14 presents two members of the
CookedBeefForDicing variant set, the CBD1 and
CBD2 products, which by means of the
chosenProduct relations specify the components of
their respective structural hierarchies.
To illustrate the use of views for inferring
implicit knowledge from the defined concepts, Fig.
15 presents some of the results of executing the
FamilyReq view. In particular, this picture shows the
material requirements of the CookedBeefRM2
family.
Figure 14: CookedBeefForDicing definition.
In Fig. 15, the [CookedBeedRM2/this_par] label
corresponds to the parameter value adopted in this
execution of the view. Two values of the STRreq
attribute are computed, corresponding to an
execution of a generic view that has the family
already mentioned as a parameter. These two values
represent alternative material requirements
corresponding to different structures. In particular,
CookedBeedRM2 either requires 1 unit of CapOf
Rump (by the CapOfRumpSTR2 structure) or 1 unit
of RumpWC (by the RumpWCSTR3 structure).
Similarly, Fig. 16 shows the results of executing the
FamilyReq view for the FrozenCookedBeef family.
A THREE LEVEL ABSTRACTION HIERARCHY TO REPRESENT PRODUCT STRUCTURAL INFORMATION
307

Figure 15: CookedBeefRM2 family requirements.
Figure 16: FrozenCookedBeef family requirements.
4 CONCLUSIONS
The main contribution of this paper is the formal
specification of PRONTO, a product information
ontology, which integrates two hierarchies: the
abstraction hierarchy (AH) and the structural one
(SH), which contains BOM related information.
The AH establishes three different abstraction
levels for the definition of products: Family,
VariantSet and Product. Such hierarchy allows
representing different granularity product data and
efficiently dealing with a high number of variants. It
uses mechanisms to maintain consistent structural
information between the different aggregation
levels. The SH organizes knowledge related to the
structural information of products. This hierarchy is
a mechanism to properly manage product
information associated with the multiple available
recipes or processes to manufacture a particular
product or a set of similar products. At each one of
the levels of the AH, the SH defines the relations
that exist between raw materials, intermediate and
final products participating in a product structure.
Another contribution of PRONTO, that is not
included in other proposals, is its intrinsic capability
of representing both, the structure of products that
are obtained by the assembly of parts (typical of
discrete manufacturing environments), as well as the
structure of those that are decomposed to obtain
intermediate products (characteristic of dairy, meat
or petrochemical industries), that can participate as
components of other products.
The proposal also manages constraints which
prevent the derivation of invalid product structures.
This feature is very important in production
environments where client specifications have a
strong influence on the definition products to be
manufactured/assembled. Thus, it avoids a client
from requiring an incorrect product configuration.
The integrated model was formalized using the
O-Telos language and implemented in ConceptBase.
This implementation provides a common vocabulary
for the definition of product structures and specifies
the semantics of each term in a non-ambiguous way
by means of first order logics. It also allowed
verifying the consistency of the proposed model,
which can be easily extended by adding new
concepts, deductive rules, queries and views.
ACKNOWLEDGEMENTS
This work has been supported by ANPCYT (PAE-
PICT2007 00051 and 02315), CONICET (PIP 2754),
UTN (PID), and UNL (CAI+D 2009).
REFERENCES
Giménez, D. M., Vegetti, M., Leone, H. P. and Henning,
G.P. 2008. PRoduct ONTOlogy: Defining product-
related Concepts for logistics planning activities.
Computers in Industry, 59, 231–241.
Giménez, D. M., Leone, H. P. and Henning, G. P. 2009. A
Hierarchical Product-Property Model to Support
Product Classification and Manage Structural and
Planning Data. LNBI, 24, 639-650.
Jarke, M., Jeusfeld, M., and Quix, C., Editors. 2004.
ConceptBase V6.2 User manual.
Mänisto, T. Peltonen, A. and Sulomen, R. (1998).
Modeling generic product structure in STEP.
Computer Aided Design, 30, 1111-1118.
ICEIS 2010 - 12th International Conference on Enterprise Information Systems
308