A GENETIC PROGRAMMING APPROACH TO SOFTWARE

COST MODELING AND ESTIMATION

Efi Papatheocharous, Angela Iasonos

Department of Computer Science, University of Cyprus

75 Kallipoleos Street, P.O. Box 20537, CY1678 Nicosia, Cyprus

Andreas S. Andreou

Department of Electrical Engineering and Information Technologies, Cyprus University of Technology

31 Archbishop Kyprianos Street, 3036 Lemesos, Cyprus

Keywords: Software Cost Estimation, Genetic Programming.

Abstract: This paper investigates the utilization of Genetic Programming (GP) as a method to facilitate better software

cost modeling and estimation. The aim is to produce and examine candidate solutions in the form of

representations that utilize operators and operands, which are then used in algorithmic cost estimation.

These solutions essentially constitute regression equations of software cost factors, used to effectively

estimate the dependent variable, that is, the effort spent for developing software projects. The GP

application generates representative rules through which the usefulness of various project characteristics as

explanatory variables, and ultimately as predictors of development effort is investigated. The experiments

conducted are based on two publicly available empirical datasets typically used in software cost estimation

and indicate that the proposed approach provides consistent and successful results.

1 INTRODUCTION

The issue of locating functions (or equations) in

software cost estimation to effectively describe

effort, usually expressed in person-months, is a long-

pursued objective in the software engineering

research and practise. Essentially a software

manager requires a viable method to predict, or at

least approximate, the total costs spent, including

money, physical and technical resources, as well as

the effort required to generate a software product

during the development process. Nevertheless, the

software industry’s inability to provide accurate

estimates of development effort is well known.

Inaccuracies of the effort required in software

projects by organizations have a strong impact on

their business continuity, reputation and

competitiveness. This occurs because effort

estimates are strongly related to correct budget and

schedule planning acquisition, while they also affect

the delivery of high quality software with the

minimum expenditures in resources. Literature

shows that the average effort overruns has not been

considerably improved over the last 10-20 years

while the fields of research for cost estimation and

industry are quite disconnected (Jørgensen and

Shepperd, 2007). The main difficulties and

limitations that impose this disconnection stem from

the dynamic nature of the software development

process. Specifically, the process faces risks

associated with the uncertain parameters at the

beginning of a new project, the lack of trained

estimators with the necessary expertise to support

the estimation process and the hindering factors

related to people, process and product developed,

that eventually affect cost. These factors relate to

high software complexity, volatile technologies,

development group dynamics and skills,

complicated team communication networks and

cohesion.

Software effort prediction is usually based on

historical project data samples either gathered within

or outside the development organization. Analyzing

the data that relate the project characteristics (of

nominal, ordinal, or numerical nature) with project

281

Papatheocharous E., Iasonos A. and S. Andreou A. (2010).

A GENETIC PROGRAMMING APPROACH TO SOFTWARE COST MODELING AND ESTIMATION.

In Proceedings of the 12th International Conference on Enterprise Information Systems - Databases and Information Systems Integration, pages

281-287

DOI: 10.5220/0002911602810287

 SciTePress

costs (primarily effort) is greatly appreciated and

required in most effort estimation models. The aim

of this paper is to attempt to offer effort prediction

with the use of evolutionary models and more

specifically structures that are automatically created

and serve as candidate solutions through Genetic

Programming (GP). These structures combine

different cost factors in simple mathematical

equations, close to regression models, which are

assessed in terms of how accurately they calculate

effort values within two cost estimation datasets.

The rest of the paper is organized as follows:

Section 2 presents a brief background review of

software cost estimation literature and presents a

short description of the methods used. Section 3

describes the use of GP on the public datasets

selected for experimentation. Section 4 presents the

basic concepts of GP and explains how these were

modified to be applied for software cost estimation.

A detailed description of how the experiments were

designed and conducted is provided in Section 5,

along with the prediction results obtained by

executing the best equations provided by the GP,

which calculate the expected effort. Finally, Section

6 presents the conclusions, discusses briefly some

limitations and outlines future research steps.

2 BACKGROUND LITERATURE

OVERVIEW

Over the last thirty years substantial work has been

conducted using estimation techniques ranging from

algorithmic and estimation-by-analogy to expert

judgement and machine learning techniques. These

techniques aim to acquire improved estimation

models that could enable project managers to

effectively manage project resources. They rely, in

a varying degree, on previous experiences or

concentrated project data to develop software cost

models. The specified information reflects previous

project experiences and typically describes the

characteristics of completed projects. Most models

developed focus on explaining the effort using a

variety of project factors, usually of a numerical

nature. More specifically, algorithmic models

attempt to introduce mathematical equations

containing cost factors for estimating the associated

development effort, usually via regression

techniques. They may also use expert judgment,

which relates to consulting several experts on the

proposed software development technique and

application domain. Well-known examples are

SLIM (Putnam, 1978), Function Points Analysis

(FPA) (Albrecht, 1979), COCOMO I (Boehm, 1981)

and the newer version of COCOMO II (Boehm et

al., 2000), etc.

Machine learning approaches in software cost

estimation, flourishing mostly in the mid 90s, reach

to better effort approximations and automate the

process of searching enhanced solutions. Such

applications include artificial neural networks

(Heiat, 2002; Papatheocharous and Andreou, 2007),

evolutionary algorithms such as genetic (Burgess

and Leftley, 2001; Lefley and Shepperd 2003;

Huang and Chiu, 2008; Razmi et al., 2009), fuzzy

logic (Xu and Khoshgoftaar 2003), etc.

It is frequently the case that machine learning

techniques are compared with the classical

regression method, which serves as the benchmark

(Burgess and Leftley, 2001; Heiat 2002; Lefley and

Shepperd 2003). The reason for applying diverging

methods over the same datasets stems from the

hypothesis that different methods may obtain a

different and more successful description of the

relationship between project attributes. However,

finding and analyzing all possible combinations of

solution relationships for estimating effort is

difficult, complex and time consuming. Thus, the

problem to determine the optimal regression

expressions in the sense of prediction ability and

relative error for cost estimation may be viewed as

an optimization problem imposing computational

challenge. Additionally, in such optimization

problems, where the search space is huge, among the

most popular techniques lay the Evolutionary

Algorithms and especially when the space involves

regression equations Genetic Programming (GP) is

considered a widely-accepted alternative. The latter

technique does not require any knowledge a-priori

and provides usually close approximations to the

optimum solution. Furthermore, unlike classical

regression approaches that assume normal

distribution for the data, it makes no such

assumptions. GP implementations may explore all

possible combinations of regression equations based

on natural evolution and on the Darwinian theory of

natural selection (Holland, 1992). GP may also be

considered a promising method for obtaining

optimized modelling of the software cost estimation

problem because it is an adaptive search technique,

able to explore a vast set of potential solutions,

which once they are obtained, they can be

comprehensively understood and easily interpreted

by individuals. More information on Genetic

Algorithms (GA) and Genetic Programming (GP)

may be found in (Koza, 1992; Michalewicz, 1994).

ICEIS 2010 - 12th International Conference on Enterprise Information Systems

282

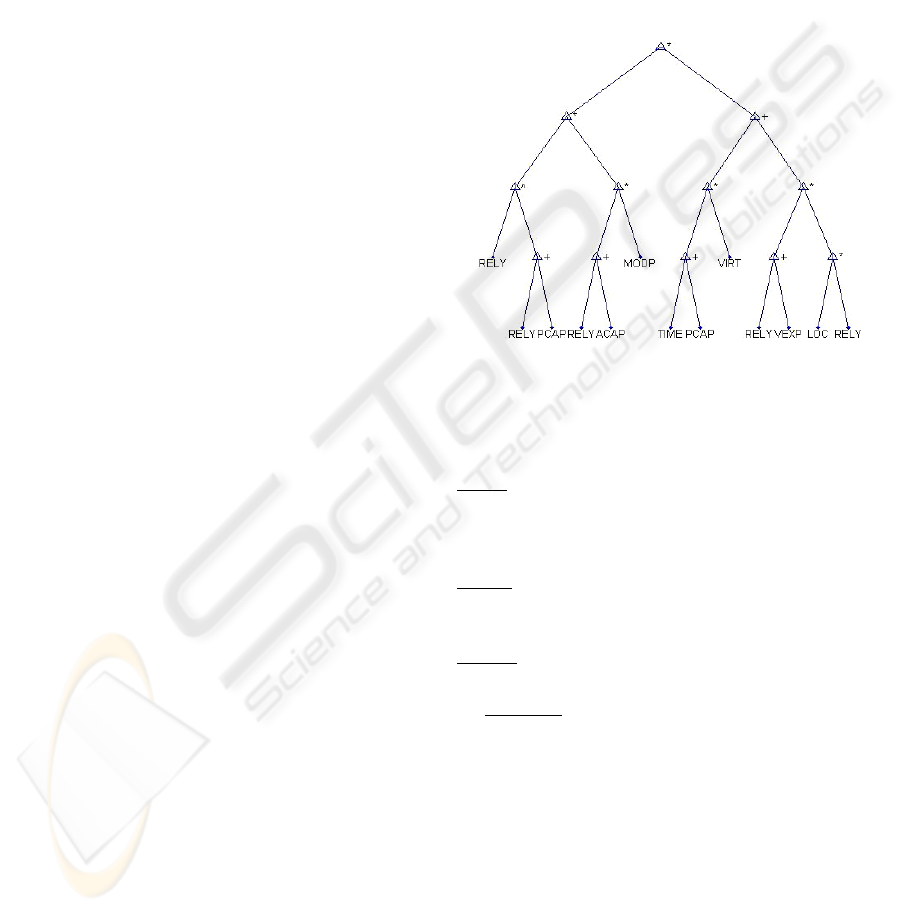
3 APPLYING GP FOR

SOFTWARE COST MODELING

The proposed implementation of Genetic

Programming (GP) seeks and locates appropriate

equations of various cost factors which characterize

the dependent variable (development effort) in the

best possible way based on specific grammars. The

overall research procedure followed was to apply GP

on two different publicly available datasets and

attempt to guide the solution towards regression

equations that provide the highest level of prediction

ability and the smallest relative error. A brief

description of the empirical datasets utilized in this

work follows.

The COCOMO dataset (Boehm, 1981) includes a

set of cost drivers that define the subjective

assessment of the product, hardware, personnel and

project attributes for 63 software projects of

different applications. The cost factors used in the

experiments are: RELY (Required Reliability),

DATA (Database Size), CPLX (Product

Complexity), TIME (Execution Time Constraint),

STOR (Main Storage Constraint), VIRT (Virtual

Machine Volatility), TURN (Computer Turnaround

Time), ACAP (Analyst Capability), AEXP

(Applications Experience), PCAP (Programmer

Capability), VEXP (Virtual Machine Experience),

LEXP (Programming Language Experience), MODP

(Modern Programming Practices), TOOL (Use of

Software Tools), SCED (Required Development

Schedule) and LOC (Lines of Code). The actual total

effort recorded in person-months against the projects

is also used to calculate the accuracy estimate

obtained by the GP regression equations.The

Desharnais dataset (Desharnais, 1989), was used

after excluding null and categorical values. It

comprised of 77 observations of systems developed

by a Canadian software development house and the

following cost features: TEAM EXP., MANAGER

EXP., LENGTH, TRANSACTIONS, ENTITIES,

POINTS AJUST, ENVERGURE, POINTS NON

AJUST. The actual development effort recorded in

person-hours was also used as the output attribute.

4 DESIGN OF THE

EXPERIMENTAL APPROACH

In the GP context, potential solutions in the

population are represented as parse trees (see Figure

1) and usually utilize a customized pool of

arithmetic operators for the case of input factors of

numerical nature. The GP tool used in the

experimental phase of this work is implemented in

Matlab v.7.5.0. (R2007b) and makes use of several

functions of the GPLab toolbox described in detail

in (Silva, 2007). The GPLab toolbox is a generic,

versatile and easily extendable tool for GP that

follows the concepts of Genetic Algorithms. Both

the manual and functions that form the toolbox are

available at http://gplab.sourceforge.net/. The basic

concepts are extended in this work by several new,

custom-built functions (also in Matlab scripts).

Figure 1: An example parse tree for COCOMO.

The GP steps executed during the experimental

process, along with the extended features are

described as follows:

Step1.

Use the software cost attributes of each

dataset to design and build a random population of

potential solutions (parse trees of regression

equations).

Step 2.

Execute each solution (parse tree) and assign

a fitness value to it according to how well the

solution describes the dependent variable (effort).

Step 3.

Generate new offspring in the population

using the following procedure:

Sampling

It defines the method for selecting a parent based

on which new individuals are created. The following

five variations are supported: Roulette, where a

roulette with random pointers is spun and each

individual owns a portion of this roulette. Sus, which

is based on the roulette process but here the pointers

are equally spaced. Tournament, where the parent is

chosen with a random draw of individuals and then

the best of them is selected. Lexictour, which is

based on tournament but in case of equality the

shortest individual wins. Double tournament, where

two tournaments are performed one for fitness and

one for parsimony. The sampling methods select the

A GENETIC PROGRAMMING APPROACH TO SOFTWARE COST MODELING AND ESTIMATION

283

best individuals according to a certain fitness

function (see equations (1) and (2)) to apply the

genetic operators listed below.

Crossover

Random nodes from two parents are chosen and

swapped creating two new individuals.

Mutation

A random node is chosen from a parent and

replaced with a randomly created tree. Several

different types are utilized here: Shrink Mutation, a

random sub-tree S is chosen from a parent and

replaced with a random sub-tree of S. Swap

Mutation, two random sub-trees are chosen from a

parent and swapped. Replace Mutation,

follows the

concepts of the normal mutation but with the

difference that for a certain mutation point

performed on a terminal node (i.e., a cost factor) the

terminal node is replaced by another random

operand from the available pool, whereas in the case

mutation is performed on an arithmetic operator, the

operator will be replaced by another randomly

selected operator from the available pool.

Survival

The selection of a number of individuals from

the current population and the newly created

children forms the new population.

Elitism

The best individuals of each generation are

passed to the next one unchanged. This is known as

the full (or total) elitism operator, according to

which the more fit individuals get the chance to be

part of the reproduction process throughout

generations.

Step 4.

Repeat steps 2 and 3 until the maximum

number of generations is reached. The solution with

the highest fitness value from the final population is

considered to be the result of the GP.

Initially, the data is randomly split in two sets, the

training and testing set, according to a percentage

defined by the user. The rationale behind this is to

produce cost functions (solutions) valid within a

variable and random set of training samples and then

evaluate their generalization performance with the

rest of the testing samples.

The cost equations make use of the following

arithmetic operators: add (+), minus (-), divide (/),

multiply (*), power (^), natural logarithm (log), base

2 logarithm (log2) and base 10 logarithm (log10).

Each equation-solution is evaluated according to the

default fitness equation (regfitness), which is later

modified to the fitness equation named mrefitness.

In the equations described x

act

represents the actual

value of the data sample and x

pred

the predicted one.

The regfitness fitness is defined in equation (1) and

calculates the sum of absolute differences between

the predicted and actual effort.

∑

−=

predact

ixixregfitness

|)()(|

(1)

The mrefitness fitness is equal to the MRE error

metric defined in the sum of equation (2) which is a

common performance metric used in the area of

software cost estimation. Additionally, common

performance metrics (equations (2)-(4)) are used for

evaluation. More specifically, the Mean Magnitude

of Relative Error (MMRE) is described in equation

(2) to evaluate the predictive ability of the

expression.

∑

−

act

predact

ixix

nMMRE

)(

)()(

)(

(2)

The Correlation Coefficient (CC) described in

equation (3), measures the ability of the predicted

samples to follow the upwards or downwards of the

original series as it evolves in the sample prediction

sequence.

⎥

⎦

⎤

⎢

⎣

⎡

−

⎥

⎦

⎤

⎢

⎣

⎡

−

−−

∑∑

∑

npred

pred

nact

act

npred

pred

nact

act

xixxix

nCC

))(())((

)])()()([(

)(

(3)

The Normalized Root Mean Squared Error

(NRMSE) described in equation (4), assesses the

quality of predictions and is calculated using the

Root Mean Squared Error (RMSE). If NRMSE=0

then predictions are perfect; if NRMSE=1 the

prediction is no better than taking prediction equal to

the mean value of n samples.

∑

−

act

actpred

xix

ixix

nNRMSE

))((

)]()([

)(

(4)

5 EMPIRICAL EXPERIMENTS

AND RESULTS

Experiments were carried out with varying

parameters, until the basic parameters of the GP

application were configured. More specifically, the

experiments were executed for a set of parameters

ICEIS 2010 - 12th International Conference on Enterprise Information Systems

284

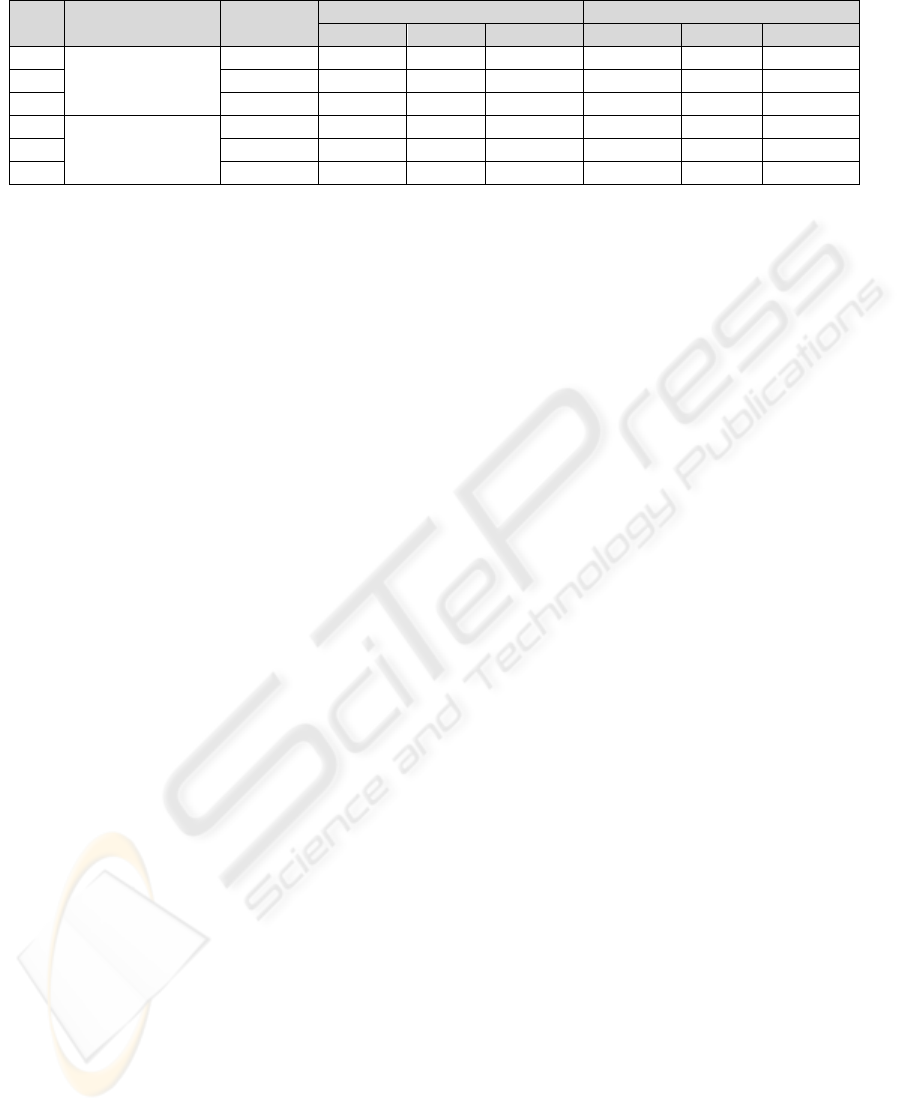
Table 1: Indicative performance results of the cost functions execution.

Rule Dataset

Depth/

Nodes*

TRAINING TESTING

MMRE CC NRMSE MMRE CC NRMSE

COCOMO

4 0.459 0.985 0.184 0.469 0.945 0.322

5 0.465 0.986 0.179 0.497 0.962 0.354

5 0.485 0.991 0.138 0.494 0.979 0.243

Desharnais

5 0.474 0.836 0.562 0.485 0.768 0.722

20* 0.520 0.799 0.606 0.521 0.731 0.684

28* 0.454 0.851 0.546 0.574 0.744 0.710

The superscript denotes tree size in terms of nodes

100 times aiming to create and evaluate diverse

equations. A random k-fold cross validation

procedure was executed, using the percentage of

80% of the historic data for constructing the solution

tree (training) and the remaining samples (20%) for

testing the prediction accuracy of the solution

(evaluation). The GP was employed on a population

of size 100 individuals and was evaluated for a

maximum of 350 generations.

Furthermore, specific parameters were selected

to create tree-structured equations that avoid

‘bloating’. Bloating is the phenomenon presented in

GP where the tree structures expand excessively

without the analogous improvement in fitness.

Several techniques exist to control bloating that

seem to have promising results to other problems,

like for example defining tree depth size and node

number restrictions on the evolved trees (Koza,

1992), setting dynamic maximum tree depth (Silva

and Almeida, 2003), applying lexictour and

doubletour sampling methods and survival methods

based on resources (Silva and Costa, 2005). For the

results presented in this section we applied Static

Resources for Survival and Total Elitism whereas

Double Tournament was used for Sampling. The

Tree Size Based on Depth was specified to values 3,

4, 5, 6 or 7 and Based on Nodes to 16, 20 or 28. The

Tree Population Type (type of trees created in the

initial population) was Ramped Half and Half

(Balanced and Unbalanced) trees. This means that

half trees were constructed based on the Maximum

Tree Level and the other half had a random form.

This ensured that the GP produced random type

trees in the initial population. For the Fitness

Improvement (describes the way the generation can

be improved) we selected the Best-of-Mean

Population Fitness which considers the fitness value

of the best-of-run mean population fitness of the

previous generation. The Expected Number of

Children (determines the method used for

calculating the expected number of children of each

individual) was set to Absolute. Additionally, the

Dynamic Maximum Tree Depth was used to control

bloat by setting a maximum depth on trees evolved,

so that when a genetic operator produces a tree that

outruns this limit, one of the parents enters the new

population instead. The Genetic Operators of

Crossover (probability=0.3), Replace Mutation

(probability=0.2) and Crossover & Mutation

(probability=0.6) were employed. The Stopping

Condition (specifies for when the algorithm should

stop) was set to either until the maximum generation

size (set to 350) is reached, or to if the best

individual produces exact results within ± the

Fitness Hits Tolerance percentage (set to 10) of the

expected results in at least the Fitness Hits

Percentage (set to 60). Finally, once the trees of the

final generation are constructed, they are evaluated

through the set of performance metrics (equations

(2)-(4)) over both the training and testing phases.

Equations (5) and (6) express two indicative cost

functions (regression equations) obtained for the

COCOMO (C

) and Desharnais (D

) datasets

respectively.

(((LOC*SCED)^(TIME/TOOL))+

((LOC^VEXP)^(TIME*MODP)))

(5)

The derived equations have a relatively simple

form and are easily understandable by project

managers. Additionally, using the best regression

equations yielded by the GP we calculated the

predicted effort values with relative high success

(see Table 1).

((((LENGTH* LENGTH)+ENVERGURE)+

((MANAGER EXP.+POINTS AJUST.)+

(TRANSACTIONS+MANAGER

EXP.)))*((POINTS NON AJUST.-

(TRANSACTIONS+ LENGTH))))

(6)

The accuracy performance for the COCOMO

and Desharnais datasets effort prediction is around

0.45 in terms of MMRE. The results in terms of the

MMRE and CC during training and testing phases

for both datasets are similar, but in terms of the

NRMSE the figures are better in training than in

A GENETIC PROGRAMMING APPROACH TO SOFTWARE COST MODELING AND ESTIMATION

285

testing. Overall, the error rates obtained are

considered quite promising in relation to other GP

approaches on the same datasets mentioned in

relative works (e.g., Burgess and Lefley, 2001,

report best population solutions for the Desharnais

dataset: MMRE=0.379 and CC=0.824). The best-of-

run equations obtained from the GP experiments

seem to perform consistently well with insignificant

differences, indicating a promising generalization

ability over the datasets employed.

6 CONCLUSIONS

The current work utilized Genetic Programming to

derive classical regression equations applied on two

publicly available project cost datasets to provide

accurate software development effort estimations.

The main contribution of this work is the automatic

creation and exploration of a large set of different

equations represented by parse trees evaluated

through newly devised fitness functions. The

experiments showed that GP performed consistently

well and reached to constructive solutions that yield

relatively successful effort approximations. This

finding is also in agreement with observations from

other research studies that compared GP to other

techniques. More specifically, the work of (Lefley

and Shepperd, 2003) focused on comparing GP with

other techniques for cost estimation. The authors

assess the accuracy of the estimates using data

within and outside organizations (SSTF dataset) and

report that GP performs very well but requires a lot

of expertise. They also emphasize the need of

producing accurate enough and simpler equations.

Similar works using the Desharnais dataset (Burgess

and Lefley, 2001) compare techniques for predicting

effort and argue that there may be other techniques

or model characteristics (despite accuracy degree)

that should have an equal, if not greater impact upon

their selection, such as ‘transparency’ and ‘ease of

configuration’. It seems that GP can produce

relatively quite transparent solutions in the sense that

they are expressed in expressions. However, again

they mention that some expertise is required to

choose configuration values for the parameters.

The present work took into consideration the

previous suggestions and attempted to obtain

simpler and suitable equations to predict effort. A

possible limitation of this work is the specific

selection of the operands used, which were

considered expressive enough to cover the potential

solution space and not too general or narrow to

radically increase execution time or constrain the

search space. Furthermore, we imposed several

restrictions to control the effect of bloat in GP

execution in order to save on both storage space and

algorithm execution time. The experiments were

designed to give a realistic dimension to the

solutions obtained in the form of equations that can

be easily interpreted and used by project managers.

Future research steps will emphasize on utilizing

operators of categorical and numerical type and

modified fitness functions that may provide

improvements to the results of the GP. Such fitness

functions could include for example combinations of

performance metrics, parameter settings and

facilitate in achieving even better effort predictions.

REFERENCES

Albrecht, A. J., 1979. Measuring Application

Development Productivity. Proceedings of the Joint

SHARE/GUIDE/IBM Application Development

Symposium, pp. 92.

Boehm, B. W., 1981. Software Engineering Economics,

Prentice Hall.

Boehm, B. W., Abts, C., Brown, A., Chulani, S., Clark B.,

Horowitz, E., Madachy, R., Reifer, D., Steece, B.,

2000. Software Cost Estimation with COCOMO II,

Pearson Publishing.

Burgess, C. J., Leftley, M., 2001. Can Genetic

Programming Improve Software Effort Estimation? A

Comparative Evaluation. Inform. and Soft. Tech., 43

(14), pp. 863-873.

Desharnais, J. M., 1989. Analyse Statistique de la

Productivite des Projects de Development en

Informatique a Partir de la Technique de Points de

Fonction. MSc. Thesis, Université du Québec,

Montréal.

Heiat, A., 2002. Comparison of Artificial Neural Network

and regression models for estimating software

development effort. Information and Software

Technology, 44, pp. 911-922.

Holland, J. H., 1992. Genetic Algorithms, Scientific

American, Vol. 267, No. 1, pp. 66–72, New York.

Huang, S.-J., Chiu N.-H., 2008. Optimization of analogy

weights by genetic algorithm for software effort

estimation. Information and Software Technology, 48,

pp. 1034-1045.

Jørgensen, M., Shepperd, M., 2007. A Systematic Review

of Software Development Cost Estimation Studies.

IEEE Transactions on Software Engineering, 33, No.

1, IEEE Computer Press, pp. 33-53.

Koza, J. R., 1992. Genetic Programming: On the

Programming of Computers by Means of Natural

Selection, MIT Press, Massachusetts.

Lefley, M., Shepperd, M.J., 2003. Using Genetic

Programming to Improve Software Effort Estimation

Based on General Data Sets, Proceedings of GECCO,

pp. 2477-2487.

ICEIS 2010 - 12th International Conference on Enterprise Information Systems

286

Michalewicz, Z., 1994. Genetic Algorithms + Data

Structures = Evolution Programs, Springer, Berlin.

Papatheocharous, E., Andreou, A., 2007. Software Cost

Estimation Using Artificial Neural Networks with

Inputs Selection. Proceedings of the 9th ICEIS, pp.

398–407.

Putnam, L. H., 1978. A General Empirical Solution to the

Macro Software Sizing and Estimating Problem, IEEE

Transactions on Software Engineering, 4 (4), pp. 345-

361.

Razmi, J., Ghodsi, R., M. Jokar, 2009. Cost estimation of

software development: improving the COCOMO

model using a genetic algorithm approach. Inter.

Journal of Management Practice, 3, pp. 346–368.

Silva, S., 2007. A genetic programming toolbox for

Matlab, Version 3, ECOS - Evolutionary and Complex

Systems Group University of Coimbra Portugal.

Silva, S., Almeida, J., 2003. Dynamic maximum tree

depth - a simple technique for avoiding bloat in tree-

based GP, Proceedings of GECCO, pp. 1776–1787.

Silva, S., Costa, E., 2005. Resource-Limited Genetic

Programming: The Dynamic Approach. Proceedings

of GECCO. ACM Press, pp. 1673–1680.

Xu, Z., Khoshgoftaar, T. M., 2004. Identification of Fuzzy

Models of Software Cost Estimation. Fuzzy Sets and

Systems, 145, No. 1, Elsevier, pp.141-163.

A GENETIC PROGRAMMING APPROACH TO SOFTWARE COST MODELING AND ESTIMATION

287