KINEMATIC IDENTIFICATION OF PARALLEL MECHANISMS BY

A DIVIDE AND CONQUER STRATEGY

Sebasti

an Durango

, David Restrepo

, Oscar Ruiz

, John Restrepo-Giraldo

and Soﬁane Achiche

CAD CAM CAE research laboratory, EAFIT University, Medell

ın, Colombia

Management Engineering Dept., Technical University of Denmark, Lyngby, Denmark

Keywords:

Parallel mechanisms, Kinematic identiﬁcation, Robot calibration.

Abstract:

This paper presents a Divide and Conquer strategy to estimate the kinematic parameters of parallel symmetri-

cal mechanisms. The Divide and Conquer kinematic identiﬁcation is designed and performed independently

for each leg of the mechanism. The estimation of the kinematic parameters is performed using the inverse cali-

bration method. The identiﬁcation poses are selected optimizing the observability of the kinematic parameters

from a Jacobian identiﬁcation matrix. With respect to traditional identiﬁcation methods the main advantages

of the proposed Divide and Conquer kinematic identiﬁcation strategy are: (i) reduction of the kinematic iden-

tiﬁcation computational costs, (ii) improvement of the numerical efﬁciency of the kinematic identiﬁcation

algorithm and, (iii) improvement of the kinematic identiﬁcation results. The contributions of the paper are:

(i) The formalization of the inverse calibration method as the Divide and Conquer strategy for the kinematic

identiﬁcation of parallel symmetrical mechanisms and, (ii) a new kinematic identiﬁcation protocol based on

the Divide and Conquer strategy. As an application of the proposed kinematic identiﬁcation protocol the iden-

tiﬁcation of a planar 5R symmetrical mechanism is simulated. The performance of the calibrated mechanism

is evaluated by updating the kinematic model with the estimated parameters and developing simulations.

1 INTRODUCTION

In mechanisms and manipulators the accuracy of the

end-effector critically depends on the knowledge of

the kinematic model governing the control model

(Zhuang et al., 1998). Therefore, to improve the accu-

racy of a mechanism its kinematic parameters have to

be precisely estimated by means of a kinematic iden-

tiﬁcation procedure (Renaud et al., 2006).

Kinematic identiﬁcation is an instance of the robot

calibration problem. The estimation of rigid-body in-

ertial parameters and the estimation of sensor gain

and offset are instances of calibration problems at the

same hierarchical level of the kinematic calibration

problem (Hollerbach et al., 2008).

This paper is devoted to the kinematic identiﬁ-

cation of parallel symmetrical mechanisms. Parallel

mechanisms are instances of closed-loop mechanisms

typically formed by a moving platform connected to

a ﬁxed base by several legs. Each leg is a kinematic

chain formed by a pattern of links, actuated and pas-

sive joints relating the moving platform with the ﬁxed

base. If the pattern of joints and links is the same for

each leg and each leg is controlled by one actuator,

then the parallel mechanism is denoted symmetrical

(Tsai, 1999).

For parallel mechanisms the kinematic identiﬁ-

cation is usually performed minimizing an error be-

tween the measured joint variables and their corre-

sponding values calculated from the measured end-

effector pose through an inverse kinematic model

(Zhuang et al., 1998; Renaud et al., 2006). This

method is preferred for the identiﬁcation of parallel

mechanisms because:

1. Inverse kinematics of parallel mechanisms is usu-

ally derived analytically avoiding the numerical prob-

lems associated with any forward kinematics solution

(Zhuang et al., 1998; Renaud et al., 2006).

2. The inverse calibration method is considered to

be the most numerically efﬁcient among the identi-

ﬁcation algorithms for parallel mechanisms (Renaud

et al., 2006; Besnard and Khalil, 2001).

3. With respect to forward kinematic identiﬁcation

no scaling is necessary to balance the contribution of

position and orientation measurements (Zhuang et al.,

1998).

In the case of parallel symmetrical mechanisms

167

Durango S., Restrepo D., Ruiz O., Restrepo-Giraldo J. and Achiche S. (2010).

KINEMATIC IDENTIFICATION OF PARALLEL MECHANISMS BY A DIVIDE AND CONQUER STRATEGY.

In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 167-173

DOI: 10.5220/0002911901670173

 SciTePress

the inverse kinematic modeling can be formulated us-

ing independent loop-closure equations. Each loop-

closure equation relates the end-effector pose, the ge-

ometry of a leg, and a ﬁxed reference frame. In conse-

quence, an independent kinematic constraint equation

is formulated for each leg forming the mechanism.

For the case of parallel symmetrical mechanisms the

set of constraint equations is equal to the number of

legs and to the number of degrees of freedom of the

mechanisms. Each kinematic constraint equation can

be used for the independent identiﬁcation of the pa-

rameters of the leg correspondent to the equation.

The independent identiﬁcation of the kinematic

parameters of each leg in parallel mechanisms allows

to improve:

1. The numerical efﬁciency of the identiﬁcation algo-

rithm (Zhuang et al., 1998).

2. The kinematic calibration performance by the de-

sign of independent experiments optimized for the

identiﬁcation of each leg.

The independent identiﬁcation of leg parameters in

parallel mechanisms was sketched in (Zhuang et al.,

1998) and developed for the speciﬁc case of Gough

platforms in (Daney et al., 2002; Daney et al., 2005).

However, the idea of the independence in the kine-

matic identiﬁcation of each leg in a parallel mecha-

nism is not completely formalized.

This article presents a contribution to the im-

provement of the pose accuracy in parallel symmet-

rical mechanisms by a kinematic calibration protocol

based on inverse kinematic modeling and a divide and

conquer strategy. The proposed divide and conquer

strategy takes advantage of the independent kinematic

identiﬁcation of each leg in a parallel mechanism not

only from a numerical stand point but also from the

selection of the optimal measurement set of poses that

improves the kinematic identiﬁcation of the parame-

ters of the leg itself.

The layout for the rest of the document is as fol-

lows: section 2 develops a literature review on the in-

verse calibration of parallel mechanisms method, sec-

tion 3 presents the divide and conquer identiﬁcation

of parallel mechanisms strategy, section 4 develops a

kinematic identiﬁcation of parallel mechanisms pro-

tocol, section 5 presents the simulated kinematic iden-

tiﬁcation of a planar 5R symmetrical mechanism us-

ing the identiﬁcation protocol, ﬁnally, in section 6 the

conclusions are developed.

2 LITERATURE REVIEW

The modeling of mechanical systems include the de-

sign, analysis and control of mechanical devices. An

accurate identiﬁcation of the model parameters is re-

quired in the case of control tasks (Hollerbach et al.,

2008). Instances of models of mechanical systems in-

cludes kinematic, dynamic, sensor, actuators and ﬂex-

ibility models. For parallel mechanisms updating the

kinematic models with accurately estimated param-

eters is essential to achieve precise motion at high-

speed rates. This is the case when parallel mech-

anisms are used in machining applications (Renaud

et al., 2006).

The inverse calibration method is accepted as the

natural (Renaud et al., 2006; Zhuang et al., 1998) and

most numerically efﬁcient (Besnard and Khalil, 2001)

among the identiﬁcation algorithms for parallel mech-

anisms. The inverse calibration method is based on

inverse kinematic modeling and a external metrolog-

ical system. The calibration is developed minimiz-

ing an error residual between the measured joint vari-

ables and its estimated values from the end-effector

pose though the inverse kinematic model. The deriva-

tion of the inverse kinematic model of parallel mech-

anisms is usually straightforward obtained (Merlet,

2006).

For our Divide and Conquer kinematic calibra-

tion strategy we adopt the inverse calibration method.

The method takes advantage of an intrinsic charac-

teristic of parallel mechanisms: the straightforward

calculation of the inverse kinematics. However, not

all the intrinsic characteristics of parallel mechanisms

are exploited. Speciﬁcally, (Zhuang et al., 1998; Ryu

and Rauf, 2001) reported that for parallel mechanism,

methods based on inverse kinematics allow to iden-

tify error parameters of each leg of the mechanism

independently. The independent parameter identiﬁca-

tion of each leg is reported to improve the numerical

efﬁciency of the kinematic identiﬁcation algorithm,

(Zhuang et al., 1998). However, it is not reported a

general kinematic identiﬁcation strategy based on the

independent identiﬁcation of the legs and its advan-

tages with respect to traditional identiﬁcation meth-

ods.

This article presents a contribution to the kine-

matic calibration of parallel mechanisms developing a

kinematic identiﬁcation protocol based on the inverse

calibration method and on the independent identiﬁca-

tion of the parameters of each leg (Divide and Con-

quer strategy).

With respect to traditional identiﬁcation methods,

our Divide and Conquer strategy has the following ad-

vantages:

1. The identiﬁcation poses can be optimized to the

identiﬁcation of reduced sets of parameters (the sets

corresponding to each leg).

2. The independent identiﬁcation of the parameters

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

168

of each leg improves the numerical efﬁciency of the

identiﬁcation algorithms.

3. By 1. and 2. the identiﬁed set of parameters is

closer to the real (unknown) set of parameters than

sets identiﬁed by other traditional calibration meth-

ods.

The divide and Conquer strategy for the inde-

pendent kinematic identiﬁcation of the parameters of

each leg in a parallel symmetrical mechanism is pre-

sented in section 3.

3 DIVIDE AND CONQUER

IDENTIFICATION STRATEGY

Parallel symmetrical mechanisms satisfy (Tsai,

1999):

1. The number of legs is equal to the number of de-

grees of freedom of the end-effector.

2. All the legs have an identical structure. This is,

each leg has the same number of active and passive

joints and the joints are arranged in an identical pat-

tern.

In a practical way, the deﬁnition of parallel sym-

metrical mechanism covers most of the industrial par-

allel structures. For parallel symmetrical mechanisms

the kinematic identiﬁcation by inverse kinematics and

a divide and conquer strategy is stated for each leg κ

independently, κ = 1, 2, . . . , n

limbs

Given:

1. A set of nominal kinematic parameters of the κth

leg (ϕ

). n

parameters are assumed to be identiﬁed:



κ,1

. . . ϕ

κ,n



(1)

2. An inverse kinematic function g

relating the κth

active joint variable (q

) with the end-effector pose

(r). For the jth pose of the mechanism the inverse

function of the κth leg is deﬁned to be:

: ϕ

×r

→ q

j = 1, 2, . . . , N.

(2)

3. A set of N end-effector measured conﬁgurations

(

) for the identiﬁcation of the κth leg:



···



(3)

4. A set of measured input variables (

) correspond-

ing to the set of end-effector measurements (



···



(4)

Goal. To ﬁnd the set of unknown (real) kinematic

parameters (

) that minimizes an error between the

measured joint variables (

) and their correspond-

ing values (

) estimated from the measured end-

effector poses by the inverse kinematic model g

. The

problem can be formally stated as the following non-

linear minimization problem:

∑

j=1



−



, ϕ





is minimum,

subject to : R

⊂ W

is the usable end −effector workspace.

(5)

The optimization problem is constrained by the

useful workspace (a workspace without singularities)

of the mechanism.

A kinematic identiﬁcation of parallel symmetrical

mechanisms protocol based on the Divide and Con-

quer identiﬁcation strategy is developed in section 4.

4 KINEMATIC IDENTIFICATION

PROTOCOL

Based on the Divide and Conquer strategy for

the kinematic identiﬁcation of parallel symmetrical

mechanisms (section 3) the following kinematic iden-

tiﬁcation protocol (Figure 1) is proposed.

1. Given the nominal parameters of the κth leg (ϕ

Eq. 1) and the correspondent inverse kinematic func-

tion (g

, Eq. 2) to calculate the κth Jacobian identiﬁ-

cation matrix of a representative set of postures of the

usable workspace:

, ϕ

) =

∂g

, ϕ

)

∂ϕ

. (6)

2. Given the Jacobian identiﬁcation matrix calculated

in the ﬁrst step to select an optimal set of postures

)) for the kinematic identiﬁcation of the κth

leg. The set of postures is selected searching the im-

provement of the observability of the set of parame-

ters ϕ

. To select the poses we adopt the active cali-

bration algorithm developed by (Sun and Hollerbach,

2008) that reduces the complexity of computing an

observability index reducing computational time for

ﬁnding optimal poses. The optimized identiﬁcation

set of postures is then deﬁned in the following man-

ner:

: O

) is maximal,

) =

√

···s

⊂ W

(7)

KINEMATIC IDENTIFICATION OF PARALLEL MECHANISMS BY A DIVIDE AND CONQUER STRATEGY

169

Calculation of the Jacobian

identification matrix

Pose selection by Active Robot Calibration

Algorithm (Sun and Hollerbach, 2008)

Estimation of kinematic parameters process

is the end-effector usable workspace

End-effector usable

workspace, W

Identified parameters,

Nominal parameters,

Inverse kinematics equation

for the κth leg:

Jacobian identification

matrix, C

Updated kinematic model

Update kinematic model

Set of optimal identification

postures, R

Set of end-effector external

measurements,

Set of active-joint

measurements,

is minimum,

Figure 1: Kinematic identiﬁcation of parallel symmetrical

mechanisms protocol.

were O

is an observability index of the identiﬁca-

tion matrix (C

, ϕ

)) of the κth leg, n

is the num-

ber of parameters to be identiﬁed in the κth leg, and

, s

. . . , s

are the singular values of the identiﬁca-

tion matrix C

. As a rule of thumb, in order to sup-

press the inﬂuence of measurement noise, the number

of identiﬁcation poses should be two or three times

larger than the number of parameters to be estimated

(Jang et al., 2001).

3. Given the optimized set of identiﬁcation postures

obtained in the second step and the correspondent sets

of active joint (

) and end-effector (

) measure-

ments to solve the optimization problem deﬁned on

Eq. 5 for the identiﬁcation of the kinematic parame-

ters (ϕ

) of the κth leg.

4. Given the identiﬁed set of parameters of the κth

leg obtained in the third step to update the kinematic

model of the parallel mechanism.

The protocol is repeated until all the legs in the

mechanism are identiﬁed.

With respect to traditional identiﬁcation algo-

rithms for the kinematic identiﬁcation of parallel

mechanism (Renaud et al., 2006; Zhuang et al., 1998)

the proposed kinematic identiﬁcation protocol has the

following advantages:

1. Reduction of the kinematic identiﬁcation compu-

tational costs. If a linear least-squares estimation of

the kinematic parameters is used to solve the identi-

ﬁcation problem (Eq. 5), then the correction to be

applied to the kinematic parameters (∆ϕ) can be esti-

mated iteratively as (Hollerbach and Wampler, 1996):

∆ϕ =





−1

∆Q. (8)

The computational cost of the matrix inversion

−1

is reduced proportionally to the square of

the number of legs of the mechanism, Table 1.

2. Improvement of the numerical efﬁciency of the

kinematic identiﬁcation algorithm by the independent

identiﬁcation of the parameters of each leg.

3. Improvement of the kinematic identiﬁcation by the

design of independent experiments optimized for the

identiﬁcation of each leg.

Table 1: Computational and measurement costs of kine-

matic identiﬁcation.

Traditional kinematic Divide and conquer

identiﬁcation identiﬁcation

Regressor C

C(N n

limbs

× N n

limbs

) C

(N × N)

Computational

cost (Matrix ∝ N

limbs

∝ N

limbs

inversion)

The kinematic identiﬁcation of parallel mecha-

nisms protocol is used in the simulated identiﬁcation

of a planar 5R symmetrical mechanism in section 5.

5 RESULTS

The results on kinematic identiﬁcation of parallel

mechanisms by a Divide and Conquer strategy are

presented using a case study: the simulated kinematic

identiﬁcation of the planar 5R symmetrical parallel

mechanism.

The planar 5R symmetrical mechanism (Figure 2)

has two degrees-of-freedom (DOF) that allows it to

position the end-effector point (P) in the plane that

contains the mechanism. The mechanism is formed

by two driving links (l

and l

) and a conducted dyad

and L

), Figure 2. The planar 5R symmetrical

mechanism is an instance of the parallel symmetrical

mechanisms deﬁned in section 3. A complete charac-

terization of the assembly conﬁgurations (Cervantes-

anchez et al., 2000), kinematic design (Cervantes-

anchez et al., 2001; Liu et al., 2006a; Liu et al.,

2006b; Liu et al., 2006c), workspace (Cervantes-

anchez et al., 2001; Cervantes-S

anchez et al., 2000;

Liu et al., 2006a), singularities (Cervantes-S

anchez

et al., 2001; Cervantes-S

anchez et al., 2000; Liu et al.,

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

170

2006a) and performance atlases (Liu et al., 2006b) are

reported. However, no research is reported on kine-

matic identiﬁcation.

P(x,y)

Leg

Figure 2: Planar 5R symmetrical mechanism.

The kinematic identiﬁcation of the planar 5R

symmetrical mechanism is simulated using the kine-

matic identiﬁcation of parallel symmetrical mecha-

nisms protocol (section 4) under the following con-

ditions:

1. A linear model is assumed for the active joint A

= kψ

+ γ

, (9)

where the k

represent the joint gain, γ

is the joint

offset, ψ

is the measured active joint angle and θ

the active joint angle, κ = 1, 2.

2. In parallel mechanisms the principal source of er-

ror in positioning is due to limited knowledge of the

joint centers, leg lengths and active joint parameters

(Daney et al., 2002). In consequence, the parameters

to be estimated are the attachment points (A

), the leg

lengths (l

, L

), and the joint gain and offset (k

, γ

κ = 1, 2:

= [l

κx

κy

]

. (10)

3. The external parameters associated with the mea-

suring device will not be identiﬁed. For the exter-

nal measuring system this implies that its position is

known and coincident with the reference frame X −Y

and the measurement target is coincident with the

end-effector point.

4. The nominal kinematic parameters of the mecha-

nism are disturbed adding a random error with normal

distribution and a standard deviation σ. The nominal

and disturbed parameters are shown in Table 2.

5. The constrain equation of the inverse kinematics

is deﬁned independently for the κth leg (Liu et al.,

2006a), κ = 1, 2:

= (x −l

cosθ

−A

κx

)

(y −l

sinθ

−A

κy

)

. (11)

6. The end-effector and joint workspace are lim-

ited by the maximal inscribed workspace (MIW),

Table 2: Planar 5R symmetrical mechanism. Nominal and

real (disturbed) parameters.

Nominal Real Nominal Real

value value value value

[m] -0.5000 -0.4988 A

[m] 0.5000 0.4961

[m] 0.0000 0.0028 A

[m] 0.0000 0.0066

1.0000 1.004 k

-1.0000 -0.9984

[rad] 0.0000 0.0048 γ

[rad] 3.1416 3.1418

[m] 0.7500 0.7507 l

[m] 0.7500 0.7559

[m] 1.1000 1.0995 L

[m] 1.1000 1.0959

Figure 2. The MIW corresponds to the maximum

singularity-free-end-effector workspace limited by a

circle (Liu et al., 2006c).

7. Each leg is identiﬁed using a set of 18 postures

of the mechanism to measure the end-effector posi-

tion and the corresponding active joint variable. The

designed sets of identiﬁcation postures in the end-

effector workspace are presented in Figure 4b.

8. The set of end-effector measurements (

) and

its corresponding active joint measurements (

) are

simulated using forward kinematics and adding ran-

dom disturbances with normal distribution and stan-

dard deviation σ = 1 ·10

−4

9. A linearization of the inverse kinematics is used for

iteratively solving the non-linear optimization prob-

lem (Eq. 5), then, for the jth identiﬁcation pose the

identiﬁcation problem of the κth leg is in the follow-

ing form:

∆q

∂g

∂ϕ

∆ϕ

= C

∆ϕ,

∆q

−

∆ϕ

−ϕ

(12)

Using N = 18 measurements to identify the set of pa-

rameters ϕ

the identiﬁcation problem is stated in the

following manner:

∆Q

= C

∆ϕ



···C



∆Q



∆q

···∆q



(13)

were C

is the identiﬁcation matrix of the κth leg. The

parameters of the κth leg can be updated using a lin-

ear least-squares solution of Eq. 13, (Hollerbach and

Wampler, 1996):

∆ϕ

= (C

)

−1

∆Q

. (14)

10. An alternative traditional kinematic identiﬁcation

by inverse kinematic modeling is calculated and used

as a comparison with respect to the proposed kine-

matic identiﬁcation protocol. The traditional identiﬁ-

cation is performed by means of a set of 36 optimized

postures selected in order to maximize the observabil-

ity of the total identiﬁcation matrix. The observability

KINEMATIC IDENTIFICATION OF PARALLEL MECHANISMS BY A DIVIDE AND CONQUER STRATEGY

171

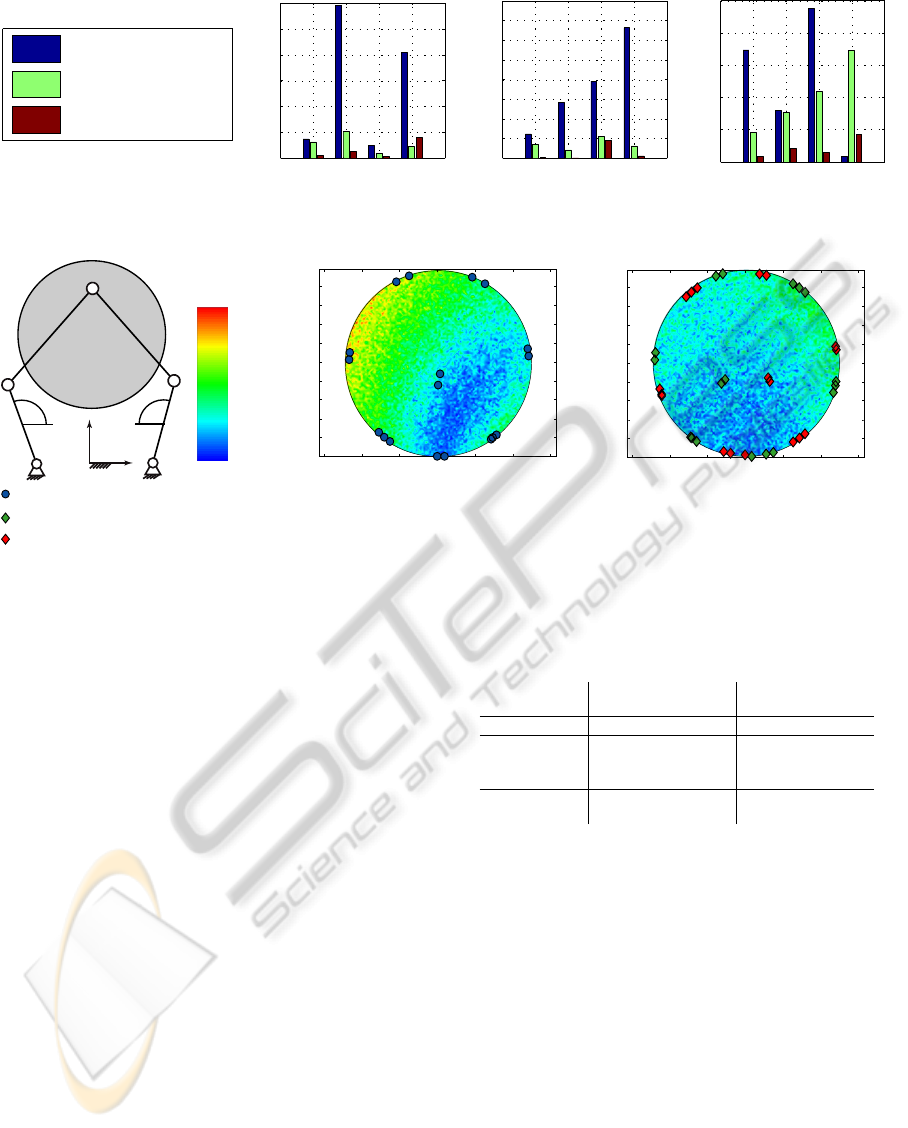
|φ

real

−φ

nominal

|φ

real

−φ

traditional Identif.

|φ

real

−φ

D&C Identif.

∆ φ [mm]

a. Link lengths

∆ φ [mm]

b. Position of fixed joints

k k

∆ φ

c. Active joint parameters

Figure 3: Planar 5R mechanism. Residual errors in the kinematic parameters before and after calibration.

−0.6 −0.4 −0.2 0 0.2 0.4 0.6

0.7

0.8

0.9

1.1

1.2

1.3

1.4

1.5

−0.6 −0.4 −0.2 0 0.2 0.4 0.6

0.7

0.8

0.9

1.1

1.2

1.3

1.4

x [m]

y [m]

x [m]

y [m]

1.19

0.89

6.68e

-03

0.30

0.60

RMSE

[mm]

P(x,y)

a) Calibration with traditional

identiﬁcation method.

b) Calibration with divide and conquer

identiﬁcation strategy.

Poses for traditional identification.

Poses for D&C identification of left leg.

Poses for D&C identification of rigth leg.

Figure 4: Planar 5R mechanism. Estimated end-effector local root mean square error for the maximal inscribed workspace

(MIW) after calibration.

was deﬁned as the Eq. 7. The designed set of identi-

ﬁcation postures is presented in Figure 4a.

The results of the kinematic identiﬁcation under

these conditions are presented in Figure 3 (residual

errors in kinematic parameters before and after cali-

bration). The residual errors are calculated as the dif-

ference between the real (virtually disturbed) param-

eters and the estimated parameters. Finally, Figure 4

presents the estimated local root mean square error for

the MIW after calibration and the selected postures

for kinematic identiﬁcation. Additionally the compu-

tational and measurement identiﬁcation costs are es-

timated for the identiﬁcation of the planar 5R parallel

mechanism, Table 3. The measurement costs of the

Divide and Conquer strategy are incremented with re-

spect to a traditional identiﬁcation method. The incre-

ment of the measurements is required because each

leg requires an independent set of end-effector mea-

surements. In the case of a traditional identiﬁcation

the set of end-effector measurements is common to all

the legs. In despite of the measurement increment the

Divide and Conquer identiﬁcation results in a supe-

rior estimation with respect to a traditional kinematic

identiﬁcation methods (Renaud et al., 2006; Zhuang

et al., 1998). The conclusions of the paper are pro-

posed in section 6.

Table 3: Planar 5R symmetrical mechanism. Computa-

tional and measurement costs of kinematic identiﬁcation.

Traditional kinematic Divide and conquer

identiﬁcation identiﬁcation

Regressor C

C(36 ×36) C

(18 × 18)

Computational

cost (Matrix ∝ 18

·2

∝ 18

·2

inversion)

Measurement 2 ·18 ·2 = 72 18 ·2(2 + 1) = 108

cost

6 CONCLUSIONS

This article presents a new (Divide and Conquer)

strategy for the kinematic identiﬁcation of parallel

symmetrical mechanisms. The new strategy devel-

ops a formalization of the inverse calibration method

proposed by (Zhuang et al., 1998). The identiﬁcation

strategy (section 3) is based on the independent identi-

ﬁcation of the kinematic parameters of each leg of the

parallel mechanism by minimizing an error between

the measured active joint variable of the identiﬁed leg

and their corresponding value, estimated through an

inverse kinematic model. With respect to traditional

identiﬁcation methods the Divide and Conquer strat-

egy presents the following advantages:

1. Reduction of the kinematic identiﬁcation computa-

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

172

tional costs,

2. Improvement of the numerical efﬁciency of the

kinematic identiﬁcation algorithm and,

3. Improvement of the kinematic identiﬁcation re-

sults.

Based on the Divide and Conquer strategy, a new

protocol for the kinematic identiﬁcation of parallel

symmetrical mechanisms is proposed (section 4, Fig-

ure 1). For the selection of optimal identiﬁcation pos-

tures the protocol adopts the active robot calibration

algorithm of (Sun and Hollerbach, 2008). The main

advantage of the active robot calibration algorithm is

the reduction of the complexity of computing an ob-

servability index for the kinematic identiﬁcation, al-

lowing to afford more candidate poses in the optimal

pose selection search. The kinematic identiﬁcation

protocol summarizes the advantages of the Divide and

Conquer identiﬁcation strategy and the advantages of

the active robot calibration algorithm.

The kinematic identiﬁcation protocol is demon-

strated with the simulated identiﬁcation of a planar

5R symmetrical mechanism (section 5). The perfor-

mance of our identiﬁcation protocol is compared with

a traditional identiﬁcation method obtaining an im-

provement of the identiﬁcation results (Figs. 3, 4).

ACKNOWLEDGEMENTS

The authors wish to acknowledge the ﬁnancial sup-

port for this research by the Colombian Administra-

tive Department of Sciences, Technology and Innova-

tion (COLCIENCIAS), grant 1216-479-22001.

REFERENCES

Besnard, S. and Khalil, W. (2001). Identiﬁable parameters

for parallel robots kinematic calibration. In IEEE In-

ternational Conference on Robotics and Automation,

2001. Proceedings 2001 ICRA, volume 3.

Cervantes-S

anchez, J. J., Hern

andez-Rodr

ıguez, J. C., and

Angeles, J. (2001). On the kinematic design of the 5r

planar, symmetric manipulator. Mechanism and Ma-

chine Theory, 36(11-12):1301 – 1313.

Cervantes-S

anchez, J. J., Hern

andez-Rodr

ıguez, J. C., and

Rend

on-S

anchez, J. G. (2000). On the workspace, as-

sembly conﬁgurations and singularity curves of the

rrrrr-type planar manipulator. Mechanism and Ma-

chine Theory, 35(8):1117 – 1139.

Daney, D., Lorraine, I., and LORIA, V. (2002). Op-

timal measurement conﬁgurations for Gough plat-

form calibration. In IEEE International Confer-

ence on Robotics and Automation, 2002. Proceedings.

ICRA’02, volume 1.

Daney, D., Papegay, Y., and Madeline, B. (2005). Choos-

ing measurement poses for robot calibration with the

local convergence method and Tabu search. The Inter-

national Journal of Robotics Research, 24(6):501.

Hollerbach, J., Khalil, W., and Gautier, M. (2008). Springer

Handbook of Robotics, Model Identiﬁcation. Springer.

Hollerbach, J. and Wampler, C. (1996). The calibration

index and taxonomy for robot kinematic calibration

methods. The International Journal of Robotics Re-

search.

Jang, J., Kim, S., and Kwak, Y. (2001). Calibration of geo-

metric and non-geometric errors of an industrial robot.

Robotica, 19(03):311–321.

Liu, X., Wang, J., and Pritschow, G. (2006a). Kinematics,

singularity and workspace of planar 5r symmetrical

parallel mechanisms. Mechanism and Machine The-

ory, 41(2):145 – 169.

Liu, X., Wang, J., and Pritschow, G. (2006b). Performance

atlases and optimum design of planar 5r symmetrical

parallel mechanisms. Mechanism and Machine The-

ory, 41(2):119 – 144.

Liu, X., Wang, J., and Zheng, H. (2006c). Optimum design

of the 5r symmetrical parallel manipulator with a sur-

rounded and good-condition workspace. Robotics and

Autonomous Systems, 54(3):221 – 233.

Merlet, J. (2006). Parallel Robots. Springer Netherlands,

second edition.

Renaud, P., Vivas, A., Andreff, N., Poignet, P., Martinet, P.,

Pierrot, F., and Company, O. (2006). Kinematic and

dynamic identiﬁcation of parallel mechanisms. Con-

trol Engineering Practice, 14(9):1099–1109.

Ryu, J. and Rauf, A. (2001). A new method for fully

autonomous calibration of parallel manipulators us-

ing a constraint link. In 2001 IEEE/ASME Inter-

national Conference on Advanced Intelligent Mecha-

tronics, 2001. Proceedings, volume 1.

Sun, Y. and Hollerbach, J. (2008). Active robot calibration

algorithm. In Robotics and Automation, 2008. ICRA

2008. IEEE International Conference on, pages 1276–

1281.

Tsai, L. (1999). Robot analysis: the mechanics of serial

and parallel manipulators. Wiley-Interscience.

Zhuang, H., Yan, J., and Masory, O. (1998). Calibration

of Stewart platforms and other parallel manipulators

by minimizing inverse kinematic residuals. Journal of

Robotic Systems, 15(7).

KINEMATIC IDENTIFICATION OF PARALLEL MECHANISMS BY A DIVIDE AND CONQUER STRATEGY

173