
OPTICAL SECURE COMMUNICATION SYSTEM BASED ON
CHAOS SYNCHRONIZATION
Alexander N. Pisarchik and Flavio R. Ruiz-Oliveras
Centro de Investigaciones en Optica, Loma del Bosque 115, Lomas del Campestre, Leon, Guanajuato, Mexico
Keywords:
Synchronization, Chaos, Secure communication.
Abstract:
We propose a secure optical communication system based on the principles of generalized and complete syn-
chronization of chaotic oscillations. Both a transmitter and a receiver are composed by two chaotic external-
cavity semiconductor lasers which are coupled in a master-slave configuration to provide generalized syn-
chronization, while the master lasers in the transmitter and in the receiver are completely synchronized via an
optical fiber. A message is added to the slave laser in the transmitter and sent to the receiver to be compared
with the output of the receiver slave laser. The system is robust to a small mismatch of the laser parameters or
of the coupling between the master and slave lasers, unavoidable in a real system, and can even enable a good
communication up to a 5 Gb/s transmission rate using the chaos masking encryption, when the master lasers
in the transmitter and in the receiver are coupled bidirectionally.
1 INTRODUCTION
Due to their high relaxation oscillation frequen-
cies (10 GHz and beyond) and direct comparability
with existing optical fiber communication technology,
semiconductor lasers have attracted much attention
from researchers working in optical communications
(Shore et al., 2008), especially after successive exper-
iments with the Athens’ fiber networks (Argyris et al.,
2005). In these lasers, high dimensional chaotic sig-
nals with a large information entropy are generated
by means of delayed feedback (Mirasso et al., 1996;
Ruiz-Oliveras and Pisarchik, 2006). The system per-
formance largely depends on the quality of chaos syn-
chronization, i.e. the synchronization error should be
minimized. Depending on the particular application
of chaotic optical communication, different encoding
and decoding schemes, such as chaos masking, chaos
shift keying, and chaos modulationwere implemented
(Tang et al., 2006). The majority of these schemes are
based on complete synchronization (CS) and use only
a single channel for both the laser coupling and the
signal transmission. A drawback of such schemes is
that CS asks for identical systems, very easy to obtain
in theory but difficult in practice.
A secure communication system based on
the concept of generalized synchronization (GS)
(Afraimovich et al., 1986) and its combination with
CS was originally suggested by Murali and Lakshma-
nan (Murali and Lakshmanan, 1998). Since they used
a single communication channel, the signal itself cre-
ated a synchronization error that reduced the commu-
nication quality. A different approach (Terry and Van-
Wiggeren, 2001) consisted of two identical pairs of
chaotic systems (master and slave); one pair in the
transmitter and the other pair in the receiver. A bi-
nary message was encrypted in the coupling strength
between master and slave in the transmitter and was
recovered by analyzing the error dynamics in the re-
ceiver; in fact, this method was a modification of a
chaos shift keying with an important innovation, it
used two channels: one to provide CS between the
transmitter and the receiver master systems, and the
other channel to compare the two slave trajectories.
However, in the chaos shift keying schemes a binary
bit message inherently produces a synchronization er-
ror, hence limiting the communication rate with the
synchronization time because the transmitter and the
receiver are not continuously synchronized.
2 COMMUNICATION SCHEME
AND LASER MODEL
We propose a new two-channel optical secure com-
munication system shown in Figure 1, which utilizes
two pairs of unidirectionally coupled external cavity
149
N. Pisarchik A. and R. Ruiz-Oliveras F. (2010).
OPTICAL SECURE COMMUNICATION SYSTEM BASED ON CHAOS SYNCHRONIZATION.
In Proceedings of the International Conference on Data Communication Networking and Optical Communication Systems, pages 149-153
DOI: 10.5220/0002912001490153
Copyright
c
SciTePress

semiconductor lasers, one pair in the transmitter, and
the other in the receiver; each consisting of a mas-
ter laser (ML) and a slave laser (SL), not necessar-
ily identical, but coupled enough to exhibit GS, while
the master lasers in the transmitter and in the receiver
should be identical (or near identical) and completely
synchronized. This scheme is completely symmetric,
the optical paths between the master and slave lasers
in the transmitter and in the recorder are the same, this
provides close similarity between their GS functions.
Such a similarity cannot be obtained if only one mas-
ter laser is coupled with two slave lasers, one in the
transmitter and one in the receiver (Yamamoto et al.,
2007; Annovazzi-Lodiet al., 2008), giving difficulties
for long distance communication.
Figure 1: Two-channel optical chaotic communication us-
ing chaos masking encryption scheme. ML
T
, SL
T
and
ML
R
, SL
R
are the master and slave lasers in the transmitter
and in the receiver, respectively, κ
T
and κ
R
are the coupling
strengths between the lasers in the transmitter and in the re-
ceiver, ε is the coupling strength between the master lasers,
and D are the photodetectors.
The external cavity semiconductor lasers can
be modeled by the following equations based on
the well-known Lang-Kobayashi approach (Mirasso
et al., 1996; Lang and Kobayashi, 1980):
˙
E
M
T,R
(t) =
1
2
(1+ iα)
G
ML
T,R
(t) −
1
τ
p
E
M
T,R
(t)+
γ
M
T,R
E
M
T,R
(t −τ
M
T,R
)exp(−iϕ
M
T,R
)+
εE
M
R,T
(t)+
q
2βN
M
T,R
(t)ξ
M
T,R
(t), (1)
˙
E
S
T,R
(t) =
1
2
(1+ iα)
G
S
T,R
(t) −
1
τ
p
E
S
T,R
(t)+
γ
S
T,R
E
S
T,R
(t −τ
S
T,R
)exp(−iϕ
S
T,R
)+
κ
T,R
E
M
T,R
(t)+
q
2βN
S
T,R
(t)ξ
S
T,R
(t), (2)
˙
N
M,S
(t) =
I
q
−
N
M,S
(t)
τ
n
−G
M,S
(t)
E
M,S
(t)
2
, (3)
G
M,S
(t) = g
N
M,S
(t) −N
0
1+ ρ
E
M,S
(t)
2
, (4)
where the subscripts M and S stand for ML and SL,
T and R stand for transmitter and receiver, E
M,S
(t)
is the slow varying electric complex field (P
M,S
=
|E
M,S
(t)|
2
being the laser output power), N
M,S
(t) is
the carrier density, α = 3 is the linewidth enhance-
ment factor, τ
p
= 2 ps and τ
n
= 2 ns are the pho-
ton and carrier lifetimes respectively, γ
M,S
is the feed-
back parameter (γ
M
T,R
= 25 ns
−1
and γ
S
T,R
= 20 ns
−1
),
τ
M,S
is the external cavity round-trip time (τ
M
T,R
= 1
ns and τ
S
T,R
= 0.5 ns), ϕ
M,S
= ωτ
M,S
is the initial
phase, ω = 1.2×10
3
ps
−1
is the angular frequency for
all lasers, β = 1.1 ps
−1
is the spontaneous emission
rate, ξ
M,S
(t) is Gaussian white noise of zero mean
and unity intensity (Heil et al., 2001), I = 29 mA is
the pump current, q = 1.602×10
−19
C is the elec-
tronic charge, g = 1.5×10
−8
ps
−1
is the gain param-
eter, N
0
= 1.5 ×10
8
is the carrier density at trans-
parency, ρ = 10
−7
is the gain saturation coefficient,
and χ = η
ext
√
1−R/(τ
c
√
R) is the coupling parame-
ter (χ = κ
T
, κ
R
, ε) (Mirasso, 2000) varied in the simu-
lations (R = 0.3 being the facet laser power reflectiv-
ity and τ
c
= 6.6 ps being the internal cavity round-trip
time, and η
ext
accounts for losses different than those
introduced by the laser facet). χ = 100 ns
−1
corre-
sponds to the case when approximately 42.8% of the
laser output power is injected into the other laser. For
the case of unidirectional coupling, ε appears only in
ML
R
.
2.1 Chaos Synchronization and
Information Transmission
To quantitatively measure synchronization, we calcu-
late the normalized cross correlation C between the
output powers of two coupled lasers (i and j)
C(t) =
P
i
(t
′
)P
j
(t
′
−t) −P
i
P
j
t
′
σ
i
σ
j
, (5)
where h...i stands for time average, P
i
, P
j
and σ
i
, σ
j
are the mean and standard deviations of the laser pow-
ers, respectively. Since in this paper we only take into
consideration isochronous synchronization, we only
calculate C(0). CS can be quantitatively character-
ized with the mean synchronization error
hei = P
i
−P
j
. (6)
Figure 2 shows C and h ei when Eqs. (5) and (6)
are used for our system; C
M
, he
M
i are calculated for
ML
R
and ML
T
[Fig. 2(a)], C
T
, he
T
i for ML
T
and
SL
T
, C
R
, he
R
i for ML
R
and SL
R
[Fig. 2(b)], and C
S
,
he
S
i for SL
R
and SL
T
[Figure 2(c)], as functions of
the coupling strengths for unidirectional and bidirec-
tional coupling between ML
T
and ML
R
. The quali-
tative behavior is similar in both cases, however for
bidirectional coupling a much smaller ε is required
DCNET 2010 - International Conference on Data Communication Networking
150
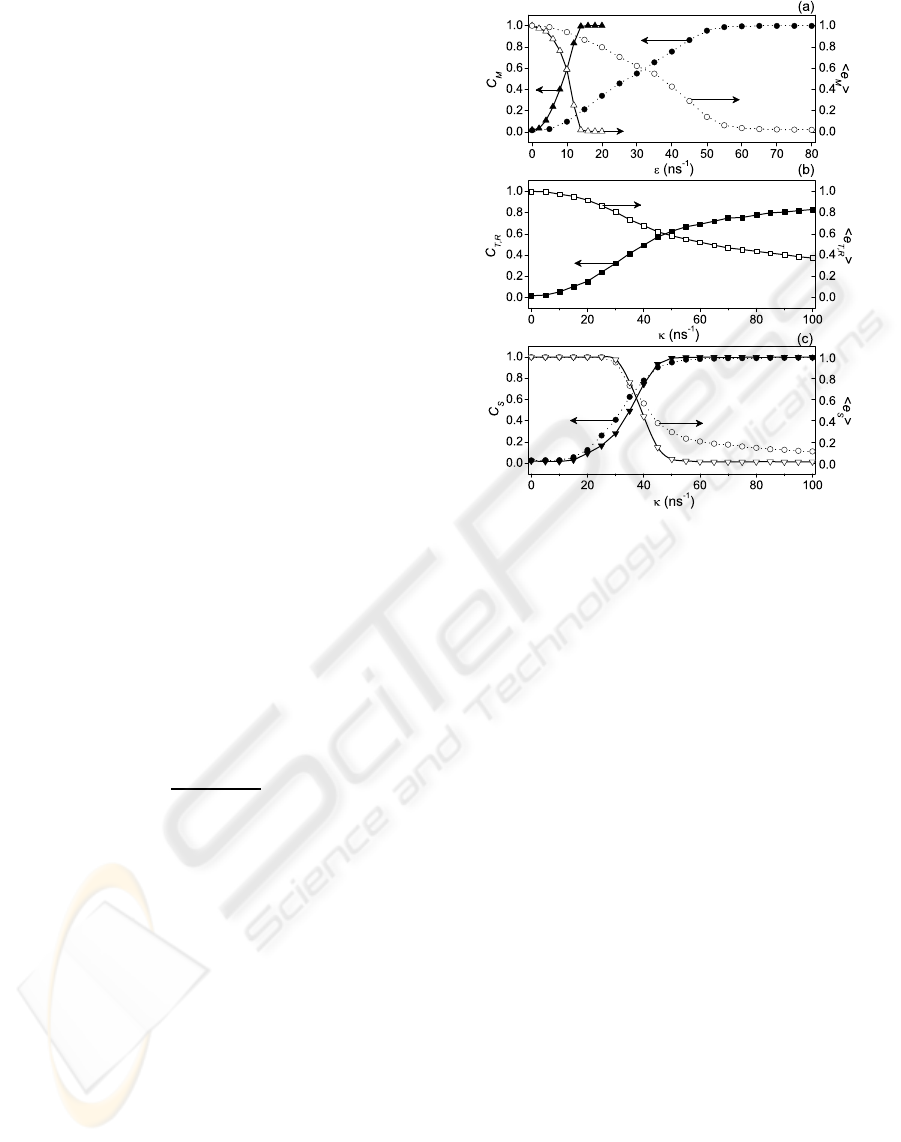
to obtain CS between the masters [Figure 2(a)] and
between the slave [Figure 2(c)] lasers. Another ad-
vantage of bidirectional coupling, very important for
security purposes, is that the transmitter has feedback
information about the receiver’s behavior, so that if
someone tried to enter the synchronization channel
in order to obtain part (or all) of the laser light, the
feedback signal would be modified. If a hacker was
able to connect with the synchronization channel, he
would use a part of the laser power to synchronize his
own laser, this would reduce the power entering to the
authorized receiver and hence the power returning to
the transmitter that could be easily identified.
Since ML and SL are not identical, we obtain GS
characterized by a relatively small cross-correlation
(C ≈ 0.8) and a high mean error (hei ≈ 0.4) for even
very strong coupling (κ = 100 ns
−1
) [Figure 2(b)].
These characteristics indicate a large difference be-
tween the laser dynamics preventing a non-authorized
person, even when he has access to both channels, to
read the message without knowing the function H.
The same curves were obtained for both the trans-
mitter and the receiver, since we supposed that their
ML and SL were coupled with the same coupling
strengths, i.e. κ
T
= κ
R
. From Figures 2(b) and 2(c),
one can see that CS between the master and slave
lasers is not needed to obtain CS between SL
T
and
SL
R
, proved even a relatively small coupling strength
(κ ≈50 ns
−1
) allows for an excellent correlation.
One way to quantitatively characterize the perfor-
mance of a communication system is Q-factor, given
by
Q =
hP
1
i−hP
0
i
σ
1
+ σ
0
, (7)
where hP
1
i and hP
0
i are the average optical powers of
bits “1” and “0”, respectively, while σ
1
and σ
0
are the
corresponding standard deviations. We prove the ben-
efits of our system with three encoding methods: (i)
chaos modulation, where the message is encrypted by
modulating the transmitter’s chaotic carrier according
to the expression (1 + m(t))E
S
exp(iφ
S
) resembling
the type of amplitude modulation (AM), (ii) chaos
shift keying, where the message is added to the pump
current of SL
T
in Eq. (2), I + m(t), inevitably pro-
ducing an error in synchronization between the slave
lasers, and (iii) chaos masking, where the message,
completely independent of the electric field, is added
to the chaotic carrier as E
S
exp(iφ
S
) + m(t) exp(iφ
m
)
(φ
m
being the message phase). In all these methods,
the message amplitude is set to a 2% of the SL
T
am-
plitude and the length of the encoded message is a
10
4
random bit sequence. The decoded message is fil-
tered with a 5th order Butterworth low-pass filter and
Figure 2: Cross-correlation (filled signs) and mean synchro-
nization error (clean signs) between (a) ML
T
and ML
R
, (b)
ML
T
and SL
T
, and (c) SL
T
and SL
R
, when ML
T
and ML
R
are coupled unidirectionally (dots) (ε = 80 ns
−1
) and bidi-
rectionally (triangles) (ε = 16 ns
−1
) as functions of their
coupling parameter. All cross-correlations are calculated in
the absence of a message.
the eye diagrams from the extracted codes are con-
structed to evaluate the transmission quality.
For the chaos modulation method, a very low Q-
factor is obtained and hence the information transmis-
sion is hardly possible. In Figure 3 we plot the values
of the Q-factor as a function of the coupling parame-
ter κ = κ
T
= κ
R
for chaos shift keying [Figure 3(a)]
and chaos masking [Figure 3(b)]. We use ε = 80 ns
−1
for unidirectionally coupled and ε = 16 ns
−1
for bidi-
rectionally coupled ML
T
and ML
R
. Note, that 5 Gb/s
good signal transmission is only possible for chaos
masking in the case of bidirectional coupling.
Finally, we consider the case when the transmit-
ter and the receiver systems are not exactly identical,
i.e. either κ
T
6= κ
R
or laser parameters exhibit a small
mismatch. Therefore, SL
R
and SL
T
are partially syn-
chronized by a certain function. Now, GS between
ML and SL in the transmitter and in the receiver
is characterized by two different functional depen-
dences, that causes a small difference betweenC
T
and
C
R
, δC = C
T
−C
R
, and we are interested in how the
mismatch δC affects communication quality. Keep-
ing all laser parameters identical and κ
T
= 80 ns
−1
for which C
T
= 0.7781 [Figure 2(b)], we vary κ
R
(60
ns
−1
≤κ
R
≤100 ns
−1
) giving as a result the variation
OPTICAL SECURE COMMUNICATION SYSTEM BASED ON CHAOS SYNCHRONIZATION
151
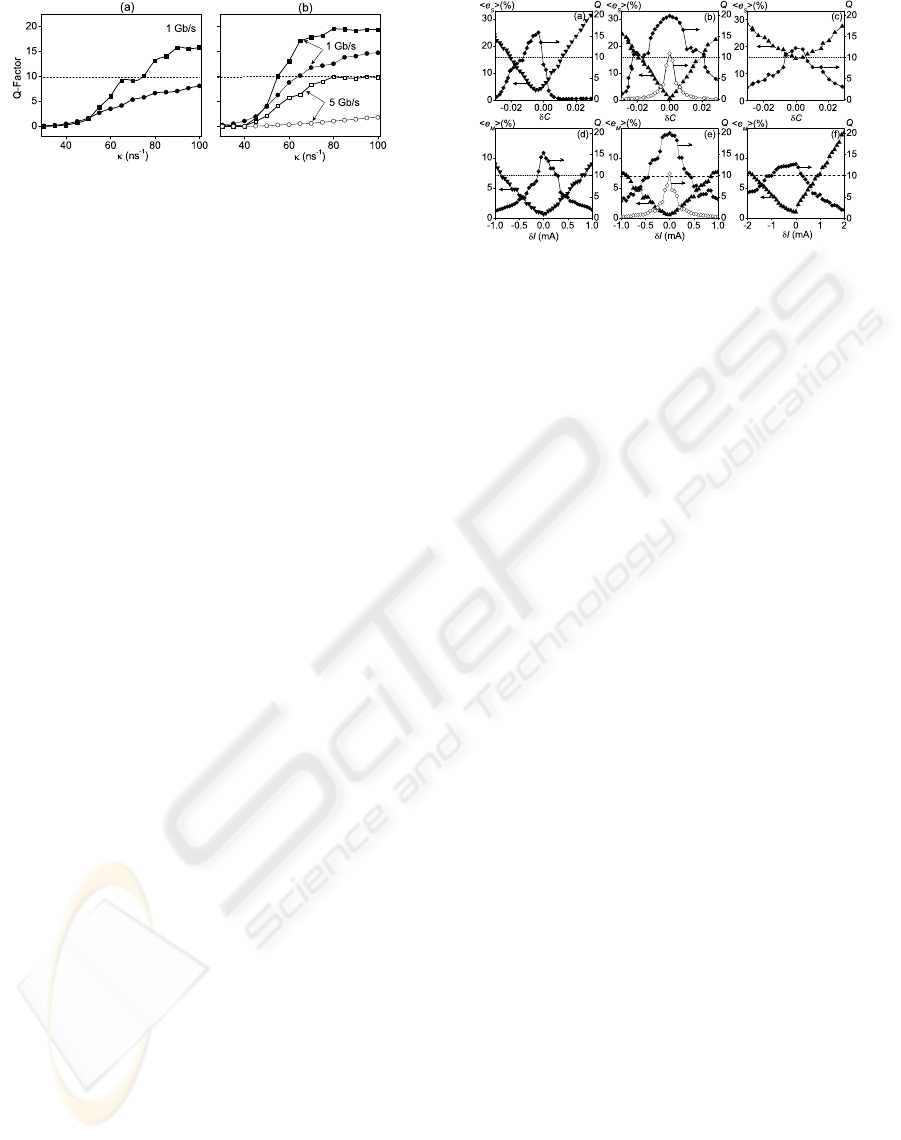
Figure 3: Q-factor as a function of coupling parameter be-
tween ML and SL for (a) chaos shift keying and (b) chaos
masking for 1 Gb/s (filled signs) and 5 Gb/s (open signs)
signal transmission when master lasers are coupled unidi-
rectionally (dots) and bidirectionally (squares) for (a) chaos
shift keying and (b) chaos masking. The communication
quality is good above the dashed line. For chaos shift key-
ing the 5 Gb/s transmission is not possible.
of C
R
(−0.04 ≤C
R
≤0.04). Figures 4(a-c) show he
S
i
(in %) and Q as functions of δC for 1 Gb/s and 5 Gb/s
transmission; Fig. 4(a) was obtained with chaos shift
keying and Figs. 4(b) with chaos masking for bidi-
rectionally coupled master lasers with ε = 16 ns
−1
.
The loss of synchronization between slaves due to the
chaos shift keying results in the displacement of the
maximum C and minimum he
S
i from δC = 0 in Fig-
ure 4(a). With the same ε Figure 4(c) represents the
results for chaos masking for unidirectional coupling,
clearly not as efficient as bidirectional coupling. The
communication quality for chaos shift keying with
unidirectionalcoupling is not sufficient (Q < 10) [Fig-
ure 3(a)]. Although chaos masking allows a 1 Gb/s
communication with unidirectional coupling, the er-
ror is relatively high (he
S
i > 15%) [Figure 4(c)].
We now also consider what happens when the
master lasers are not completely identical, keeping
κ
R
= κ
T
. In this case, the most critical parameter for
synchronization is the injection current. Figures 4(d-
f) show how a small mismatch δI = I
T
−I
R
(I
T
and
I
R
being the injection currents of the master lasers in
the transmitter and in the receiver) affects he
M
i and
Q. One can see that when the master lasers are cou-
pled bidirectionally, the system is more robust to a
parameter mismatch, i.e. the 1 Gb/s transmission can
be realized in a much larger region of δC or δI, and
even a 5 Gb/s rate can be obtained but only for chaotic
masking and only when the slave lasers and the mas-
ter lasers are completely synchronized, i.e. when the
identity conditions, δC ≈ 0 and δI ≈ 0, are fulfilled.
Figure 4(d) shows that chaos key shifting even for 1
Gb/s is not as efficient as chaos masking.
Figure 4: Mean synchronization error (triangles) and Q-
factor (dots) as functions of mismatch of (a-c) correlations
δC and (e-f) injection currents δI of master lasers for chaos
shift keying (left-hand column) and chaos masking (middle
and right-hand columns) when the master lasers are cou-
pled either bidirectionally (left-hand and middle columns)
or unidirectionally (right-hand column). 1 Gb/s and 5 Gb/s
transmission are shown by the closed and open dots, respec-
tively. κ
T
= 80 ns
−1
, ε = 16 ns
−1
for bidirectionally and
ε = 80 ns
−1
for unidirectionally coupling, and I
T
= 29 mA.
The communication quality is good above the dashed lines.
3 CONCLUSIONS
We have introduced an efficient optical chaotic com-
munication system which uses the combination of
complete and generalized synchronizations. The sys-
tem contains two channels, one for synchronization
and the other for information transmission, and con-
sists of two pairs of external cavity semiconductor
lasers each coupled in GS configuration, while the
master lasers in the transmitter and in the receiver
are completely synchronized. The ability of this
system for high-quality communication is demon-
strated through numerical simulations with the Lang-
Kobayashi model. We have shown that bidirectional
coupling between the master lasers provides much
better communication quality (up to 5 Gb/s) than uni-
directional coupling and makes the system more ro-
bust to a mismatch between the ML parameters or the
coupling strengths between ML and SL. In the case
of bidirectional coupling, the two coupled lasers in-
fluence to each other so that the identity requirements
for complete synchronization are not as strong as in
the case of unidirectional coupling that allows more
tolerances. The efficiency of this system is very clear
when the encryption method is chaos masking, it can
also be used for other methods although the results
are not so spectacular.
DCNET 2010 - International Conference on Data Communication Networking
152

ACKNOWLEDGEMENTS
This work was supported by Consejo Nacional de
Ciencia y Tecnologa of Mexico (project No. 100429).
REFERENCES
Afraimovich, V. S., Verichev, N. N., and Rabinovich, M. I.
(1986). Stochastic synchronization of oscillation in
dissipative systems. Quant. Electron., 29:795–803.
Annovazzi-Lodi, V., Aromataris, G., Benedetti, M., and
Merlo, S. (2008). Secure chaotic transmission on a
free-space optics data link. IEEE J. Quantum Elec-
tron., 44:1089–1095.
Argyris, A., Syvridis, D., Larger, L., Annovazzi-Lodi, V.,
Colet, P., Fischer, I., Garc´ıa-Ojalvo, J., Mirasso, C. R.,
Pesquera, L., and Shore, K. A. (2005). Chaos-based
communications at high bit rates using commercial
fibre-optic links. Nature, 438:343–346.
Heil, T., Fischer, I., Els¨asser, W., Mulet, J., and Mirasso,
C. R. (2001). Chaos synchronization and spontaneous
symmetry-breaking in symmetrically delay-coupled
semiconductor lasers. Phys. Rev. Lett., 86:795–798.
Lang, R. and Kobayashi, K. (1980). External optical feed-
back effects on semiconductor injection laser proper-
ties. IEEE J. Quantum Electron., 16:347–355.
Mirasso, C. R. (2000). Applications of semiconductor
lasers to secure communications. In Nonlinear Laser
Dynamics: Concepts, Mathematics, Physics, and Ap-
plications International Spring School, AIP, Confer-
ence Proceedings, pages 112–127, Washington, DC.
Mirasso, C. R., Colet, P., and Garcia Fernandez, P. (1996).
Synchronization of chaotic semiconductor lasers: Ap-
plication to encoded communications. IEEE Photon.
Tech. Lett., 8:299–301.
Murali, K. and Lakshmanan, M. (1998). Secure communi-
cation using a compound signal from generalized syn-
chronizable chaotic systems. Phys. Lett. A, 241:303–
310.
Ruiz-Oliveras, F. R. and Pisarchik, A. N. (2006). Phase-
locking phenomenon in a semiconductor laser with
external cavities. Opt. Express, 14:12859–12867.
Shore, K. A., Spencer, S. P., and Pierce, I. (2008). Recent
Advances in Laser Dynamics: Control and Synchro-
nization, chapter Synchronization of chaotic semicon-
ductor lasers, pages 79–104. Research Singpost, Ker-
ala.
Tang, S., Chen, H.-F., and Liu, J.-M. (2006). Digital Com-
munications Using Chaos and Nonlinear Dynamics,
chapter Performance of synchronized chaotic optical
communication systems, pages 341–378. Institute for
Nonlinear Science. Springer, New York.
Terry, J. R. and VanWiggeren, G. D. (2001). Chaotic
communication using generalized synchronization.
Chaos, Solitons and Fractals, 12:145–152.
Yamamoto, T., Oowada, I., Yip, H., Uchida, A., Yoshi-
mori, S., Yoshimura, K., Muramatsu, J., Goto, S.,
and Davis, P.(2007). Common-chaotic-signal induced
synchronization in semiconductor lasers. Opt. Ex-
press, 15:3974–3980.
OPTICAL SECURE COMMUNICATION SYSTEM BASED ON CHAOS SYNCHRONIZATION
153
