A CASTOR WHEEL CONTROLLER FOR DIFFERENTIAL DRIVE

WHEELCHAIRS

Bernd Gersdorf

Safe and Secure Cognitive Systems, German Research Center for Artiﬁcial Intelligence, Bremen, Germany

Shi Hui

SFB/TR8 Spatial Cognition, University of Bremen, Germany

Keywords:

Differential drive vehicle, Electric wheelchair, Castor wheel, Motion controller, Force compensation.

Abstract:

This paper describes a motion controller for differential drive vehicles with a compensation for castor wheel

turn forces. The controller has been developed for electric wheelchairs with two front castor wheels, which

require large steering forces to move into the direction given by the joystick in situations where a sharp turn

of the castor wheels is needed. It computes the required forces to turn the castor wheels and modiﬁes the drive

request adequately. This also helps physical or cognitive impaired users who otherwise have to compensate

castor turn forces manually using the joystick, which requires fast reaction time (e.g. when the castor wheels

turn quickly into the driving direction) to avoid collisions.

1 INTRODUCTION

Figure 1 presents the intelligent wheelchair ROLLAND

(Lankenau and R¨ofer, 2001) based on a Meyra

wheelchair of the model CHAMP (Meyra Ortopedia,

2010). As many other electric wheelchairs, CHAMP

uses pneumatic tires for both back differential drive

wheels and front castor wheels to achieve comfort-

able indoor and outdoor driving. The conﬁguration

of back differential drive and two front castor wheels

is probably the most frequently used one for electric

wheelchairs. With the large ground contact area of

the castor wheels, the high load (typical 160kg for

the wheelchair with the driver, about one third on the

front axis), and the tire material (rubber), the addi-

tional force to change the angle of the castor wheel

is signiﬁcant, especially when maneuvering at low

speed in a narrow environment. Recently, an empiri-

cal study (reference skipped) on the evaluation of the

safety assistant modul developed for ROLLAND was

carried out, which monitors the surrounding environ-

ment using sensor data gathered by the equipped laser

scanners and brakes in time if an obstacle is danger-

ously close to the wheelchair. During the experiment

a common phenomenon was observed: after the in-

tervention of the safety assistant, the participants at-

tempted to regain control over the wheelchair by givi-

Figure 1: The intelligent wheelchair ROLLAND.

ng driving commands via the joystick, but the

wheelchair did not drivein the direction they expected

or did not move at all.

The primary reason for such problems is that the

wheelchair requires a lot of motor force to turn the

castor wheels, if the wheelchair starts in a standing

position with castor wheels positioned in a blocking

state (i.e., the two castor wheels stand transversely to

the required drive direction). Moreover, users often

change the joystick command if the wheelchair does

not react to the previously given command, as most

participants did in the above study. As a result they

tried to give the wheelchair some arbitrary commands

174

Gersdorf B. and Hui S. (2010).

A CASTOR WHEEL CONTROLLER FOR DIFFERENTIAL DRIVE WHEELCHAIRS.

In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 174-179

DOI: 10.5220/0002913101740179

 SciTePress

via the joystick or pressed the joystick powerfully,

which caused an even less expected behaviour of the

wheelchair. One solution to this problem, and as the

focus of the current paper, is to apply a castor wheel

controller, which enables the wheelchair to adjust cas-

tor wheels correctly, such that the time delay to realize

the requested drive command can be reduced in those

situations, and the joystick can remain in a stable po-

sition.

Castor wheels have been investigated in the liter-

ature mainly to model and minimize wheel shimmy

(see (de Falco et al., 2009), (Brearley, 2009), (Kau-

zlarich et al., 2000)). In (Kauzlarich et al., 1984), cas-

tor turn forces are compared for different grounds and

tire materials, but without a projection of these forces

to the differential drive of an electric wheelchair.

Therefore no compensation of these forces is dis-

cussed in that work.

This paper is structured as follows: We begin in

Section 2 with the kinematic model for differential

drive wheelchair with two front castor wheels, and

introduce a model to predict castor turn forces and

discuss possible compensation. Section 3 explains

the integration of the castor force compensation into

ROLLAND. Section 4 discusses some test results by

comparing the wheelchair behaviour with and without

the castor controller. Before concluding in Section 6

we discuss some related approaches in Section 5.

2 A KINEMATIC MODEL

We are going to present a kinematic model of cas-

tor turn forces for differential drive wheelchairs with

two front castor wheels. The castor wheel angles are

essential for the required turn forces, thus should be

discussed ﬁrst.

2.1 Castor Wheel Angles

Forward

a a

′

Figure 2: Determination of castor wheel angles.

To compute the required force to turn the castor

wheels, the castor angles must be computed based on

the current driving request. The motion state of dif-

ferential drive vehicles can be described by its rota-

tional speed ω (rad/s) and translational speed υ (m/s)

measured at the center point C between the powered

wheels. The radius r (see Figure 2) is determined by

= ω ⇔ r =

(1)

However, there is always a small gap c between a cas-

tor’s ground touch point and the intersection of its

steering axis with the ground plane (also called trail).

Furthermore, the steering axis inclination is usually

0 or almost 0 for castor wheels, and can be assumed

to be 0. If c equals 0, the angle of the castor can be

obtained (using trigonometry) by

tanα =

r− b

(2)

For 0 < c ≪ a (as usual), the castor wheel angle α

obtained by Equation 2 is already a good approxima-

tion. However, a higher precision α

′

can be obtained

using the ground touch point at distances a

′

and b

′

derived from the ﬁrst estimation of the castor wheel

angle α and the value of the gap c (see Equation 5),

with which more precise castor turn forces can be cal-

culated.

′

= a− c∗ cosα (3)

′

= a− c∗ sinα (4)

tanα

′

r− b

′

(5)

2.2 Castor Turn Forces

a τ

Figure 3: Castor turn force F projected to differential drive

wheels.

Figure 3 shows the geometry of the ROLLAND electric

wheelchair as an example for a differential drive robot

with two castor wheels. Let the castor turn force F be

the force that is required to start the castor wheel to

swivel without rotating the wheel and applied at the

castor steering joint. This force must be applied per-

pendicular to the drivingdirection of the castor wheel.

F can be split into

F = F

ground

+ F

joint

(6)

A CASTOR WHEEL CONTROLLER FOR DIFFERENTIAL DRIVE WHEELCHAIRS

175

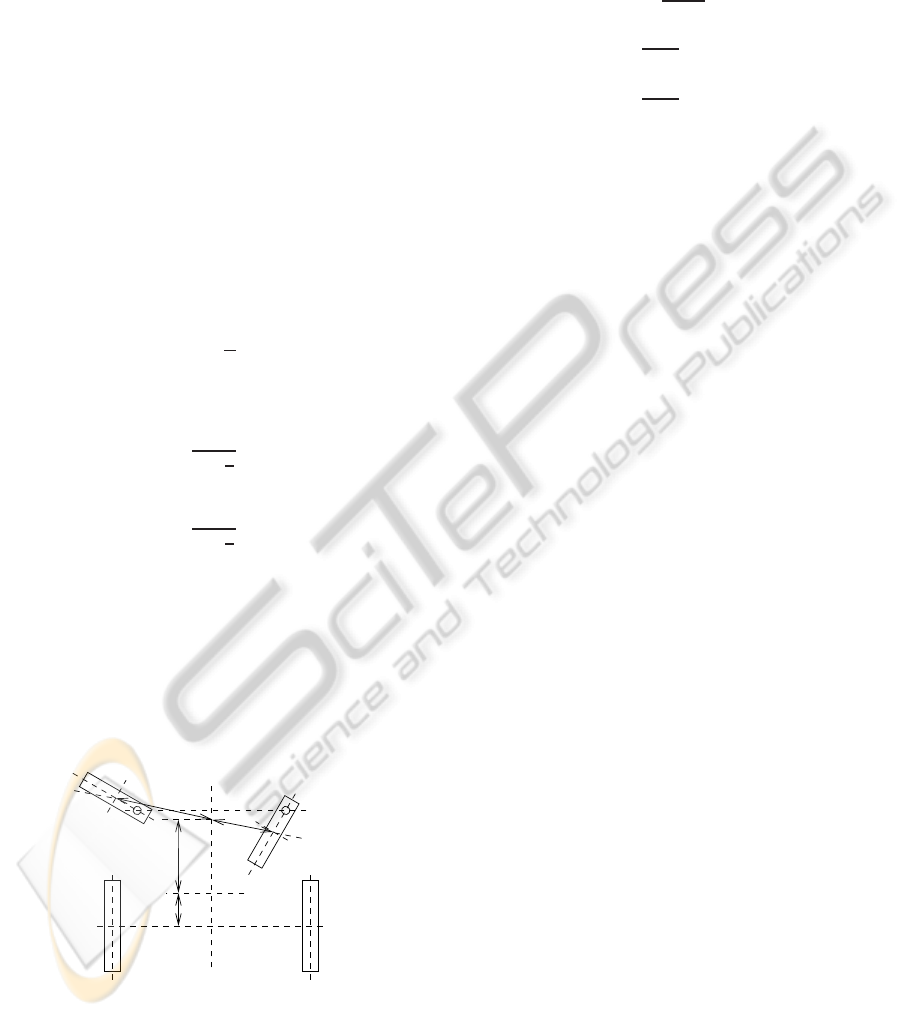
where F

ground

represents the friction between the

ground and the tire at the ground touching point, and

joint

the friction inside the turning joint. The joint

is typically so constructed that F

joint

≪ F

ground

. A

difference between sticking and gliding forces could

not be observed, due to the plasticity of the tire. As

frictional forces grow proportionally with the normal

force between the surfaces, the castor turn forces can

be described as

F = c

castor

L (7)

where L is the load of the castor wheel and c

castor

is constant for a given wheelchair and ground mate-

rial. Equation 7 must be understood as an upper limit

of the required castor force. A rolling castor wheel

requires much smaller turn forces, which should be

considered by the castor controller (see Section 3).

The castor turn force can be projected to the forces

of the two differential drive wheels, F

and F

(see

Figure 3):

θ = α±

(8)

F =

(9)

= F

cosτ

(10)

tanτ

b−

(11)

= F

cosτ

(12)

tanτ

(13)

+ or − in Equation 8 is chosen depending on the in-

tended castor steering direction (left or right swivel).

Equation 9 splits the castor correction force

F into

forces of the differential drive wheels. The left en-

gine produces

as the sum of the motor force

and

a shearing force

(see Figure 3). The left engine

force F

is computed by Equations 10 and 11, and the

right one by Equations 12 and 13.

Figure 4: Mass distribution to castor and differential drive

wheels.

Figure 4 shows the center of mass M of the

wheelchair at the point with a distance of p to the back

axis. The back wheels are connected with springs to

the chassis, such that both wheels can be assumed

to carry the same weight that sums up to M

at the

back axis center. The front wheels carry the remain-

ing mass M

, giving the following mass distribution:

= M

p+ q

(14)

l + r

(15)

l + r

(16)

The values for p, l, and r can be obtained from the

ground touch points as in Figure 2.

2.3 Maximal Castor Turn Forces

Using the kinematic model of Sections 2.1 and 2.2,

Figure 5 gives an overview of the forces required by

the differential drive vehicle using the geometry of

the Meyra CHAMP wheelchair (in mm: d = 585, p =

160, a = 470, b = 42). For each value of the left cas-

tor angle (x-axis), the diagram shows the angle of

the right castor wheel, which maximises the required

correction force for one of the two differential drive

motors. The force factor (right y-axis in Figure 5)

is the relation between the required motor force and

the standard situation in the left diagram of Figure

6, where castor turn forces and engine forces are all

equal, and the castor wheels are in a blocking state

when drivingforward. The diagram in Figure 5 shows

two symmetric maximal force factors −2.21 (left en-

gine) and 2.21 (right engine). The −2.21 maximum

for the left drive wheel is also shown in the right

diagram of Figure 6 with castor angles L = 46.08

◦

R = 8.28

◦

3 MOTION CONTROLLER

The kinematic model described in Section 2 has

been implemented and integrated into the wheelchair

ROLLAND in two ways:

• as an add-on for a classical proportional-integral

(PI) controller using odometry information to

control translational and rotational wheelchair

speed (used for autonomous driving).

• as a pure castor force compensation controller to

support joystick driving.

Although the tests reported in Section 4 have been run

with the pure castor controller, both controllers have

been implemented using the following principles:

1. The castor controller applies a slowly growing

correction force. This helps to adapt to different

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

176

-60

-30

120

150

180

210

240

0 30 60 90 120 150 180 210 240 270 300 330 360

-4

-3

-2

-1

right castor angle [degree]

engine force [factor]

left castor angle [degree]

right=1.23

left=-2.21

left=-1.23

right=2.21

left engine force

right engine force

right castor angle

Figure 5: Castor angles with maximal differential drive load.

Figure 6: Castor correction forces in standard (left) and

maximized situation (right).

frictional forces for varying undergrounds, stand-

ing or rolling castor wheels. It smoothly applies

forces for the transition from standing still (no

correction forces applied) to driving (correction

applied).

2. The correction force will be signiﬁcantly reduced,

if the castor wheel turns too fast.

3. The correction force is reduced, when the differ-

ence between actual and requested castor angle is

small.

4. If the given command changes the driving direc-

tion, the control intensity is reduced. A control in-

tensity built for a speciﬁc driving direction should

not be applied for a completely different driving

direction.

5. The correction force of the controller is reduced to

zero, if one of the castor correction forces changes

its sign (the castor angle has crossed its target an-

gle). This allows to reach the target castor angle

exactly and reduces oscillations around the ideal

castor angle.

6. The mass distribution to each individual wheel

can be signiﬁcantly inﬂuenced by the differential

drive forces. The Meyra CHAMP, for example,

has an independent wheel suspension using a trail-

ing arm for each wheel. The forward torque of a

wheel moves the trailing arm and its wheel down-

ward, which increases the load of the castor wheel

on the opposite side. The measurements of this ef-

fect have been used in the controller to correct the

mass distribution described in Figure 4.

7. If the differential drive stands still, the engine

torques grow nonlinear with the given driving

command. The relation between them has been

measured and recorded in a table to apply correct

forces.

The combination of the castor controller with a PI-

controller requires to join the drive requests produced

by both controllers. A brief impression can be ob-

tainded by the following two principles:

• For small deviating castor angles, the inﬂuence of

the castor controller should be small. This gives

priority to the PI-controller.

• Correction forces of the castor controller are sub-

tracted from integral parts of the PI-controller.

This gives priority to the castor controller, if cas-

tor wheels are in a blocking state.

A CASTOR WHEEL CONTROLLER FOR DIFFERENTIAL DRIVE WHEELCHAIRS

177

-0.5

0.5

1.5

0 1000 2000 3000 4000 5000 6000 7000

rad/s or rad

time in ms

(3) 50% engine force

(5) 20% engine force

(1)

(2)

(6)

(4)

(1) castor left angle (rad)

(2) castor right angle (rad)

(3) steering (blocked, rad/s)

(4) rotation (blocked, rad/s)

(5) steering (unblocked, rad/s)

(6) rotation (unblocked, rad/s)

Figure 7: Wheelchair behaviour for a left turn with blocking or adjusted castor wheels.

4 TEST RESULTS

In order to evaluate the inﬂuence of the pure castor

wheel controller, a number of tests have been carried

out using the wheelchair ROLLAND. In the following

we are going to discuss some test results.

The test shown in Figure 7 compares the reaction

of the wheelchair between blocked and unblocked

castor wheels while making a left turn without a cas-

tor controller. The steering command for blocked (3)

and unblocked (5) castor wheels is slowly increased

to a level that moves the wheelchair. With unblocked

castor wheels, the engine force can be limited to 20%

(5) to reach a wheelchair turn speed of about 0.6 rad/s

(6). For blocked wheels, the engine force must be in-

creased to 50% (3) to let the castor wheels turn around

(angles are shown in (1) and (2)). In this case, the

castor wheels start to swivel after about 5 seconds.

The steering command is then reduced to zero (dur-

ing this measurement) to avoid a too fast rotation of

the wheelchair. Usually, the steering command must

be reduced by the wheelchair user manually.

The adjustment of giving steering commands by

the pure castor controller is demonstrated by Figure

8. The diagram shows a left-turn of the wheelchair

starting with castor wheels in a blocking state using

the castor controller. It compares the given steering

command (5) from the user and the motor commands

for steering (3) and forward motion (4) computed by

the controller. The forward motor command is the

mean value of left and right motor command, and

the steering motor command the difference between

them. The controller uses the driving command and

the castor angles of the left (1) and right (2) wheels

as input values. It produces a peak for the left en-

gine of about 80% power (computed from forward

(3) and steering (4) motor command), and will be re-

duced when the castor wheels start to swivel. The

wheelchair starts to turn around signiﬁcantly after the

peak is reached, as indicated by curve (6) measured by

the odometry of the wheelchair. The castor controller

reacts much earlier than an odometry based controller

and releases the user from doing this manually.

5 RELATED APPROACHES

An alternative approach is to turn the castor wheels

using an additional actuator, as for the Toyota PM re-

search vehicle (Toyota Motor Sales USA, 2009; Bon-

sor, 2004). The trail of the castor wheel can then

be 0, which makes it 180

◦

rotation symmetric. The

wheelchair manufacturer Otto Bock recently pre-

sented the XENO wheelchair with a steering system

called S

(Single Servo Steering, (Otto Bock Health-

Care GmbH, 2010)) in combination with a differen-

tial drive using an approach similar to that of the PM

research vehicle. For the additional cost of the cas-

tor turn servo engines, the Otto Bock system releases

the differential drive from the burdon of castor turn

forces, but the time to turn the front wheels can be

signiﬁcantly longer than the time needed to turn clas-

sical castor wheels. This can confuse a user who is

unaware of this fact.

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

178

-1

-0.5

0.5

1.5

2.5

0 1000 2000 3000 4000 5000 6000 7000

-200

-100

100

200

300

400

500

600

rad/s or rad

mm/s

time in ms

(3) 80% power

(1)

(2)

(4)

(5)

(6)

(1) castor left angle (rad)

(2) castor right angle (rad)

(3) steering motor command (rad/s)

(4) forward motor command (mm/s)

(5) steering input command (rad/s)

(6) wheelchair rotation speed (rad/s)

Figure 8: Castor controller for a left turn with blocking castor wheels.

6 CONCLUSIONS

In this paper we presented a castor wheel controller

for differential drive wheelchairswith two front castor

wheels (e.g., ROLLAND based on a Meyra wheelchair

of type CHAMP). The controller uses the devel-

oped kinematic model to project turn forces of castor

wheels to engine torques of differential drivevehicles.

Some test data were given to compare the steering be-

haviour with and without the controller. The major

beneﬁt of the castor wheel controller is to release the

user from the task to compensatethe castor turn forces

using the joystick to simplify the driving with the joy-

stick.

One future work is to do more experimental eval-

uation and performance analysis of the pure and com-

bined castor wheel controllers before carrying out real

user studies. Moreover, the measurement of castor an-

gles through potentiometers is unprecise in a certain

range of angles. We will replace them by magnetic

angle measurement sensors for full coverage.

REFERENCES

Bonsor, K. (2004). How the Toyota PM works. Technical

report, Toyota Motor Sales, U.S.A., Inc,.

Brearley, M. N. (2009). Investigation of castor-wheel

shimmy. Journal of Mechanics and Applied Mathe-

matics, 33(4):491–505.

de Falco, D., Massa, G. D., and Pagano, S. (2009). On

the castor dynamic behavior. Journal of The Franklin

Institute, to appear.

Kauzlarich, J. J. P., Bruning, T. E., and Thacker, J. G. P.

(1984). Wheelchair caster shimmy and turning re-

sistance. Rehabilitation Research and Development,

20(2):15–29.

Kauzlarich, J. J. P., Bruning III, T. E., and Thacker, J. G. P.

(2000). Wheelchair caster shimmy II: Damping. Re-

habilitation Research and Development, 37(3):305–

313.

Lankenau, A. and R¨ofer, T. (2001). A safe and versatile mo-

bility assistant. IEEE Robotics and Automation Mag-

azine, 1(7):29–37.

Meyra Ortopedia (2010). Electric-wheelchairs CHAMP

1.594. http://www.meyra.de/meyraweb/o

basis.pl.

Otto Bock HealthCare GmbH (2010). XENO - stand up

and go! http://www.ottobock.com/.

Toyota Motor Sales USA (2009). The personal mo-

bility vehicle. http://www.toyota.com/concept-

vehicles/pm.html.

A CASTOR WHEEL CONTROLLER FOR DIFFERENTIAL DRIVE WHEELCHAIRS

179