
DISTRIBUTED OPTIMIZATION BY WEIGHTED ONTOLOGIES
IN MOBILE ROBOT SYSTEMS
Lucia Vacariu
1
, George Fodor
2
1
Department of Computer Science, Technical University of Cluj Napoca, 26 Baritiu str, Cluj Napoca, Romania
2
ABB AB Process Automation, Vasteras, Sweden
Gheorghe Lazea, Octavian Cret
Department of Automation, Technical University of Cluj Napoca, Cluj Napoca, Romania
Department of Computer Science, Technical University of Cluj Napoca, Cluj Napoca, Romania
Keywords: Mobile cooperating robots, Heterogeneous agents, Subgradient optimization, Distributed ontology.
Abstract: Heterogeneous mobile robots are often required to cooperate in some optimal fashion following specific
cost functions. A global cost function is the sum of all agents’ cost functions. Under some assumptions it is
expected that a provable convergent computation process gives the optimal global cost for the system. For
agents that can exchange ontological information via a network, different variables in the global vector are
relevant when ontology instances have been recognized and communicated among agents. It means the
optimization depends on what is known to each agent at the current time. There are two ways to solve an
optimization of this kind: (a) to weight agents according to the ontology instances or (b) to add ontology-
defined optimization constraints. This paper illustrates the benefits of the weighted optimization method.
1 INTRODUCTION
Intended applications for the optimization method
proposed in this paper are systems of cooperating
robots, where each robot is designed using an agent
architecture. Each robot has specific sensors and
actuators, thus robots and agents are in general
heterogeneous.
In order to fulfil goals at an abstract level, agents
can exchange ontological information (Văcariu,
Chintoanu, Lazea and Creţ, 2007). As shown in
Section 2, ontological concepts are mapping the
sensed world with non-trivial modes of actuation
and goal seeking. Using a symbolic layer with
ontologies means that agents can undergo rather
discontinuous changes when recognizing different
types of environment that are associated to complex
actions and goals.
It is typical for applications with many sensors,
actuators and high-level of intelligence that the same
goal could be achieved in many ways and at
different costs. Thus optimization of cost functions
of agents is an important requirement for a practical
solution. We consider a total number of M agents
acting in all the robots; each agent has an index i
(i=1,…,M) and a related convex cost function f
i
(x).
The argument x is a vector in R
n
of resources.
Initially, agents know their own resources but they
have a degree of uncertainty about the resources
available to other agents. In time, each agent tries to
compute the best estimate of the resource vector x
that optimizes the agent’s own cost function. By
exchanging resource vectors and ontologies among
agents, the optimization can make a better resource
allocation using common resources. Thus, the cost
function for each agent converges to an (almost)
optimal value and the overall cost function
∑
=
=
M
i
i
xfK
1
)(
will be also minimized.
In our model, the non-smooth cost functions
obtained by discrete changes in resource vectors by
ontology update are not differentiable over the
whole domain, thus these functions are optimized by
a subgradient method (Shor, Kiwiel, and
Ruszcaynski, 1985).
180
Vacariu L., Fodor G., Lazea G. and Cret O. (2010).
DISTRIBUTED OPTIMIZATION BY WEIGHTED ONTOLOGIES IN MOBILE ROBOT SYSTEMS.
In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 180-185
DOI: 10.5220/0002914701800185
Copyright
c
SciTePress

2 AGENT MODEL
In traditional applications, the components of a
resource vector used for optimization are physical
measured values. In more advanced applications,
resource vectors change, an interesting case being
when agents exchange ontologies.
Here we describe the relationship between the
resource vector x and the symbolic part of the agents
ontological representation.
We consider that each robot is built on an agent
architecture that can host a number of specialized
agents. These can use local robot resources. We
have a set of cooperating robots Ro, indexed from 1
to M. The set of sensors of a system of robots is:
Se: Ro x Ns (1)
where Ns = number of sensors.
The decisions made by agents are not based
directly on raw sensor data. Normally, a so called
perception relation is the result of processing the
data from several sensors. For a robot with Kr
sensors, a perception relation is defined as a
mapping of sensors to indices Np:
Re: Se
Kr
x Np (2)
Perception relations are associated symbolic
names by a mapping from the set of perception
relations Re to a vocabulary (set of words) Tv called
symbolic perceptions:
RelS:
|
Re
|
x N → Tv
(3)
where |Re| is the index of a relation in (2) and N is
the index of the robot.
Ontology is a formal representation of a set of
concepts within a domain and the relationship
between these concepts (Noy and McGuinness,
2001). These concepts being specific to a domain, it
generally means that there is no obvious one-to-one
mapping between ontological concepts and the
perception relations. If the set of ontological
concepts is Z, a robot-specific ontology is defined as
the relation between the perception relations and a
relationship between a set of L ontological concepts:
Ont: Tv → Z
L
(4)
Depending on the inclusion relation between the
specific ontology and the perception relations, there
are three cases. A specific ontology is (1)
fundamental when
LKr
ZSe ≡
; (2) is minor relative
to the perception relations if
LKr
ZSe ⊂
; (3) is
major relative to perception relations if
LKr
ZSe ⊃
.
We consider here major specific ontologies.
Agents are using the actuator gear of robots to
achieve goals. Actuators are denoted:
Ac: Ro x Na (5)
with Na being the actuator index and Ro the set of
robots. A relation of actuation is a mapping from the
symbolic perceptions Tv to actuators:
RelA: Tv → Ac
(6)
which shows the intended action for each symbolic
perception in Tv. Finally, it is assumed that since
each action is executed under known conditions, the
intended effect of the action is known as a specified
next symbolic perception. This is called the
actuation effect relation (or actuation relation) EfA:
EfA: Ac x Tv → Tv
(7)
The dynamics of the data evaluation is shown in
the Figure 1 below:
RelS
Tv
Z
L
EfA
Figure 1: Data evaluation.
3 MULTI-AGENT MODEL
In the multi-agent system each robot has a number
of agents, each agent having a specific set of
relations of the type (1) – (5). All agents are
assumed to use the same domain ontology since this
ensures that common goals can be achieved and that
communication is not robot manufacture-dependent.
Each agent has only a subset of the common domain
ontology, subset that was considered appropriate for
its sensors, actuators and goals at the design time.
During the cooperation phase, agents are exchanging
information such as sensor data, ontology concepts
or resource vectors. It is also assumed that all agents
have a bounded communication time interval T.
There are several mechanisms for ontological
communication but we describe only the method
called Simple Ontological Substitution (SOS).
Let t
a
and t
c
be two symbolic perceptions in the
Tv set of a local agent such that according to relation
(7), we have t
c
= EfA(a
c
,t
a
) (Figure 2).
DISTRIBUTED OPTIMIZATION BY WEIGHTED ONTOLOGIES IN MOBILE ROBOT SYSTEMS
181

t
a
c
a
t
c
t
b
a
b
Local agent executing SOS
Remote agent
Figure 2: Simple Ontological Substitution.
Formally, the intended sequence towards a goal
is as follows: sensors of the local agent expect
reading data which is used to interpret the symbolic
perception t
a
as true. The associated actuation a
c
is
expected to materialize the symbolic perception t
c
.
However, the environment of the robot changes such
that no symbolic perception among those of the T
ν
set of the local agent will become true. The agent
cannot recognize the environment state in which it
acts. The local agent has information according to its
EfA relation about the wanted perception to realize
t
c
. Another agent in some remote robot has a
corresponding relation EfA of the type t
c
= EfA(_,_).
The local agent is sending a request for all agents in
the system, with the following content: (a) a remote
agent should have the EfA resulting in t
c
and (b) the
remote agent should send this EfA together with the
corresponding Z
L
(see Figure 1) to the local agent.
If such a remote agent exists, and answers with
the t
c
= EfA(a
b
,t
b
), then the local agent will ask for
the execution of a
b
that will result in t
c
. Next time,
when a similar situation happens, the local agent has
the ontology knowledge to cope with this situation.
4 OPTIMIZATION
4.1 Optimizing Individual Agents
Each agent i, i = 1,…,n has an individual cost
function f
i
: R
n
→ R expressing e.g. energy, material
or wear and tear costs. A minimum value of the cost
function means finding a so called optimal resource
vector x* such that:
f
i
(x*) ≤ f
i
(x)
∀
x ∈ R
n
(8)
All cost functions are assumed convex:
f(ta + (1 – b)t) ≤ tf(a) – (1 – t)f(b)
(9)
For each convex function a local optimum is also
a global optimum. This makes the computation of an
optimum easy when the function is smooth (it has
derivatives of high order). For example, from the
truncated Taylor expansion:
2
2
)("
)(')()( h
xf
hxfxfhxf ++≈+
,
by differentiation on h we obtain
0)('
2
)("
2 =⋅+⋅⋅ dhxf
xf
dhh
, and after reductions,
)("
)('
xf
xf
h −=
. This gives the iteration which is
Newton’s method for solving
0)(' =xf
(k is the
iteration index).
x
k+1
= x
k
+ h (10)
The example above shows the two important
parts of a program solving an optimization
application (Bonnans, Gilbert, Lemaréchal, and
Sagastizábal, 2002):
(a) The Algorithm for Searching the x Space.
This
manages the update of the argument x to the fastest
convergence rate of the sequence x
1
, x
2
,…, x
k
,…, x*.
There are two types of search methods: one is a
direct search, i.e. the traditional Nelder-Mead
method (Fletcher, 2003); the other is to use
information about the functions to be optimized,
such as its higher derivatives. For example, the
corresponding of the Newton method (relation (10))
for the multi-dimensional case is:
)()(
1
1 kkfkk
xfsHxx ∇−=
−
+
(11)
To determine the iteration step, must be solve the
linear system: H
f
(x
k
)s
k
= – ∇f(x) such that relation
(11) becomes x
k+1
= x
k
+ s
k
.
(b) The Simulator. For each new iteration
determined by the search algorithm, a computation
is done using the new x in the problem P to be
optimized to find a gradient descent or an equivalent
“good” direction. Often the initial problem P is
replaced by a simpler problem P
k
which computes a
direction along a line of the solution.
The method can be illustrated with subgradients
on non-smooth functions. Let f(x) to be a non-
smooth, convex function, defined on R, with values
in R (Figure 3). Let x
0
be a point of discontinuity of
the function. A subgradient is any line of direction c
containing the point (x
0
, f(x
0
)), such that: f(x) – f(x
0
)
≥ c(x – x
0
), a line “below” a convex function and
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
182
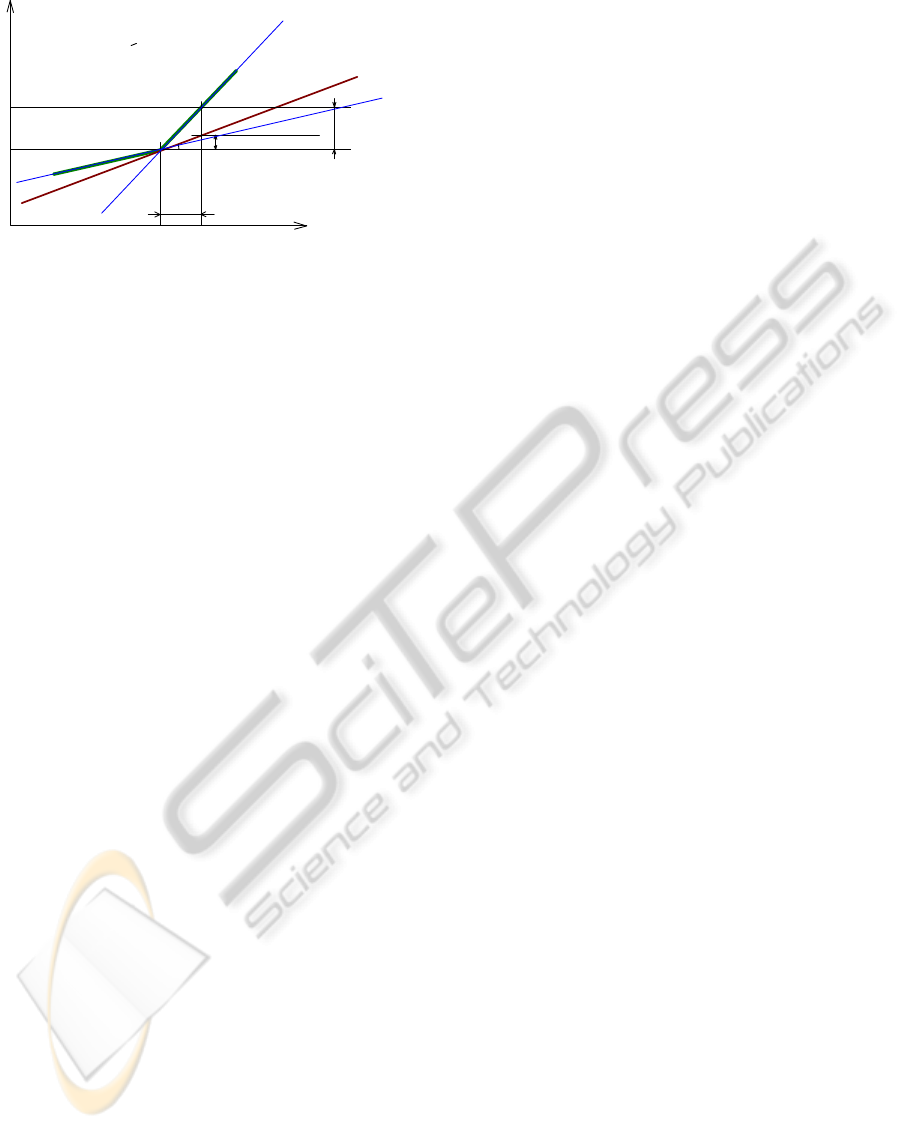
x
f(x)
x0
x
f(x)
f(x0)
f(x)-f(x0)
x-x0
subgradient
f(x)
a
tg(a)*(x-x0) = c(x-x0)
f(x)-f(x0)>c(x-x0)
S1
S2
Figure 3: Subgradient in R
1
.
which intersects the function in only one point.
For vectors in R
n
a subgradient is a vector s
f
(x
0
)
such that:
f(x) – f(x
0
) ≥ s
f
(x)
T
(x – x
0
)
(12)
The set of all subgradients of f at x
0
is called the
subdifferential of f at x
0
and it is denoted as
∂
f(x
0
). In
Figure 3 the subdifferential is the set of lines through
the point (x
0
, f(x
0
)) placed between the lines S1 and
S2 defined by the directions of the non-smooth
function. Using the results obtained until now, the
iterative algorithm for an agent i at iteration k+1 is:
x
i
(k+1) = x
i
(k) –
α
i
(k)d
i
(k)
(13)
where
α
i
(k) is the size of the step used by agent i and
d
i
(k) is a subgradient of agent’s i objective function
at x
i
(k).
4.2 Optimization of the Multi-agent
System
A global optimization means that a vector x*
representing common resources to all agents,
minimizes the sum of cost functions f
i
(x*) of each
agent i. Initially, before a new optimization cycle
begins, each agent may have different values for its
vector x. However, the size of the vector and the
resource or physical meaning of each element in the
vector is common to all agents.
An algorithm shown to converge for optimizing
multi-agent systems (Nedic, Ozdaglar, 2009), uses
the subgradient method shown in formula (13), but
with the difference that at each step k, an agent
combines its resource vector with a weighted value
of the resource vectors of all other agents. For an
agent i, its weight relative to an agent j at iteration k
is
Rkw
j
i
∈)(
. Weights are normalized
1)(
1
=
∑
=
M
j
j
i
kw
for each agent i and each iteration k. With this
change, formula (13) becomes:
)()()()()1(
1
kdkkxkwkx
i
ij
M
j
j
i
i
⋅−⋅=+
∑
=
α
(14)
The index j ranges over all M agents. As in
relation (13),
α
i
(k) is a scalar being the step size
used by agent i and d
i
(k) is a vector in R
n
, the
subgradient of agent’s i objective function at x
i
(k).
While the weights in the work of Nedic and
Ozdaglar (2009, p. 49) uses a concept of agents
close to each other, in this work we use information
about shared ontologies and EfA relations described
in (7) and Figure 1.
4.3 Optimization in the Presence of
Ontological Communication
The relative weight of agent i to agent j,
)(kw
j
i
,
shows how “close” resources of the two agents are.
Resources can be “close” even when their physical
nature is very different.
Using ontologies, as shown in relations (3)-(7)
and Figure 1, an agent can determine which
resources are used as these are mapped to
ontologies. As agents act continuously, the weights
)(kw
j
i
change to reflect that some other set of
resources are currently used.
The resource vector is a vector x ∈ R
N
, so it
contains as components only numerical, real values.
In the chain of relations RelS
→
T
ν
→
Z
L
,
information from sensors are interpreting perception
relations RelS, which are determining which
symbols in Tv have the value True, which are
determining which ontological concepts are
identified. When an ontological concept is
identified, it means all its properties are considered
to hold.
It is important that at each new symbolic
perception, the corresponding ontology is shared
with other agents. Some of the previous resources
will still be used while some new are going to be
used. The choice of the weights
)(kw
j
i
must reflect
these transitions.
Thus, to find the weight factor among agents
means determining a concept of distance among
ontologies. One definition for distance uses a tree-
ontology metrics: a distance using a formal
representation of the ontology, by a measure of the
path length between concepts. According to this
measure, if c
1
and c
2
are two nodes in a formal
representation of the ontology, l is the shortest path
between the concepts and h is the depth of the
DISTRIBUTED OPTIMIZATION BY WEIGHTED ONTOLOGIES IN MOBILE ROBOT SYSTEMS
183
deepest concept subsuming both concepts, then the
distance between c
1
and c
2
is
hkhk
hkhk
lk
ee
ee
eccsim
22
22
1
)2,1(
−
−
−
+
−
⋅=
(15)
(k
1
and k
2
are scaling parameters for the shortest path
vs. the depth) (Debenham, and Sierra, 2008). This
type of measure can be done for asserted ontologies.
Another style of metrics is based on set-theoretic
principles, by counting intersections and unions of
ontological concepts. Best known is Tversky’s
similarity measure between two objects a and b and
with properties (feature sets) A and B:
||)),(1(||),(||
||
),(
ABbaBAbaBA
BA
bas
−−+−+∩
∩
=
αα
(16)
where |.| is the cardinality of the set, minus is the set
difference and
α
(a,b) in the interval [0,..,1] is a
tuning factor that weights the contribution of the
first reference model (Tversky’s similarity measure
is not symmetrical).
Besides Tversky’s measure, similarity measure
functions available in most scientific mathematical
libraries are, for example Cosine, Dice, Euclidian,
Manhattan or Tanimoto.
The algorithm for using any of the similarity
measures above to determine the weight between
two agents is the following:
1. Generate the set of all ontological properties (both
numerical and non-numerical) of agent i as a union
of all ontological properties valid at iteration k. Let
this set be A and the cardinality of the set be |A|;
2. Generate in the same manner the set of all
ontological properties for agent j; let this set be B
with cardinality |B|;
3. Compute the cardinality of the intersection, union,
differences, symmetric difference, as needed by the
selected similarity formula;
4. Compute the similarity index. The resulting value
is the weight
)(kw
j
i
.
5 EXAMPLE
To demonstrate the weighted method we present an
example with a cooperation multi-robot system used
in supermarket supervision. Two of the robots in the
system have both common and distinct sensors.
Robot 1, Ro1, has sensors (see relation (1)):
Distance = Se(1,1); Shape (cube, cylinder, sphere) =
Se(1,2); Dimensions (length, width, height,
diameter) = Se(1,3); Temperature = Se(1,4); Colour
= Se(1,5).
The second robot, Ro2, has sensors to obtain
information for: Distance = Se(2,1); Shape =
Se(2,2); Dimensions Se(2,3); Weight = Se(2,4).
Combining Ro1 sensors information, we obtain
possible perception relations (see relation (2)), e.g.:
Re([Se(1,1), Se(1,2), Se(1,3)], 1) – for a
combination of Distance, Shape and Dimension and
Re([Se(1,1), Se(1,4), Se(1,5)], 5) – for a
combination of Distance, Temperature and Colour.
These perception relations have associated
symbolic perceptions (see relation (3)), as shown in
Table 1.
Table 1: Symbolic perceptions Ro1.
Index Re Perception Relation Re
Tv
(symbol)
1 Distance < 10m AND Shape =
Parallelepiped AND Dimension >
10m x 2m x 2m
shelf
2 Distance < 5m AND Shape =
Parallelepiped OR Cube AND
Dimension < 1m x 1m x 0.5m
box
3 Distance < 5m AND Shape =
Sphere AND Dimension < 1m
ball
4 Distance < 5 m AND Shape =
Sphere AND Dimension < 0.5m
balloon
5 Distance < 50m AND
Temperature > 200
0
C AND Colour =
Red OR Orange
fire
6 Distance < 10m AND
Temperature > 50
0
C AND Colour =
White OR Yellow
lamp
A similar computation for robot 2 gives the
results in Table 2.
Table 2: Symbolic perceptions Ro2.
Index
Re
Perception Relation Re
Tv
(symbol)
1 Distance < 10m AND Shape =
Parallelepiped AND Dimension > 10m x 2m
x 2m
shelf
2 Distance < 5m AND Shape =
Parallelepiped OR Cube AND Dimension <
1m x 1m x 0.5m AND Weight > 3 kg
box
3 Distance < 5m AND Shape =
Parallelepiped AND Dimension < 1.5m x
0.5m x 1m AND Weight < 3 kg
cart
We have now two sets of symbols for the two
robots (agents): P={shelf, box, ball, balloon, fire,
lamp} and Q={shelf, box, cart}. We compute the set
operations required e.g. using the “dice” similarity
measure:
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
184
bothABonlyBonlyA
bothAB
BAsim
dice
⋅++
⋅
=
2
2
),(
|P
∪ Q| = |{shelf, box, ball, balloon, fire, lamp,
cart}| = 7; |P-Q| = |{ball, balloon, fire, lamp}| = 4
and |Q-P| = |{cart}| = 1. So the weight
2
1
w between
agent 1 and 2 is:
73,0
7214
72
2
1
=
⋅++
⋅
=w
.
The full matrix of weight is computed in this
fashion for all agents.
The example is using three agents with three
different cost functions of type
2
2
2
1
)( BxAxxf +=
,
with parameters from Table 3.
Table 3: Agents cost functions.
Agent A B Init vector
Agent 1 0.5 2.5 [1 3]
Agent 2 1.0 4.0 [3 6]
Agent 3 3.0 1.0 [4 5]
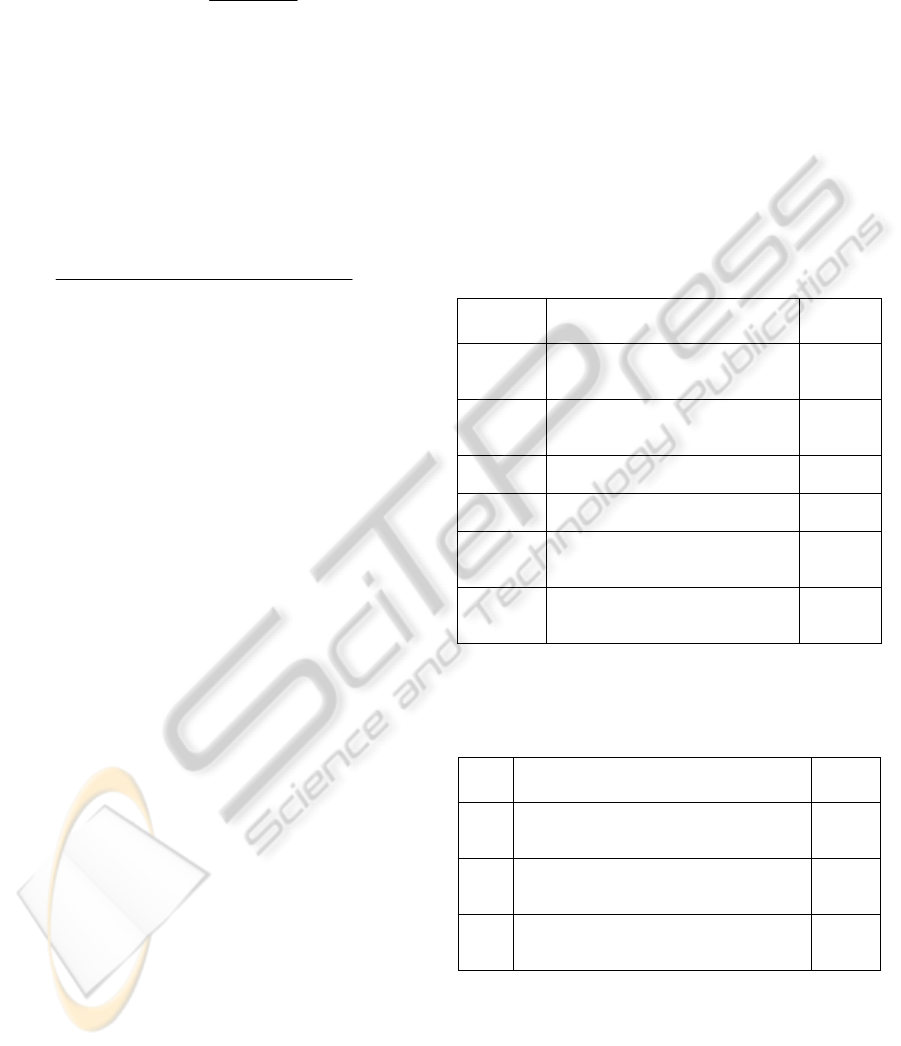
Figure 4 shows that indeed vectors converge
towards the intended minimum value [0 0].
−2 −1 0 1 2 3 4
−2
−1
0
1
2
3
4
5
6
Figure 4: Convergence results.
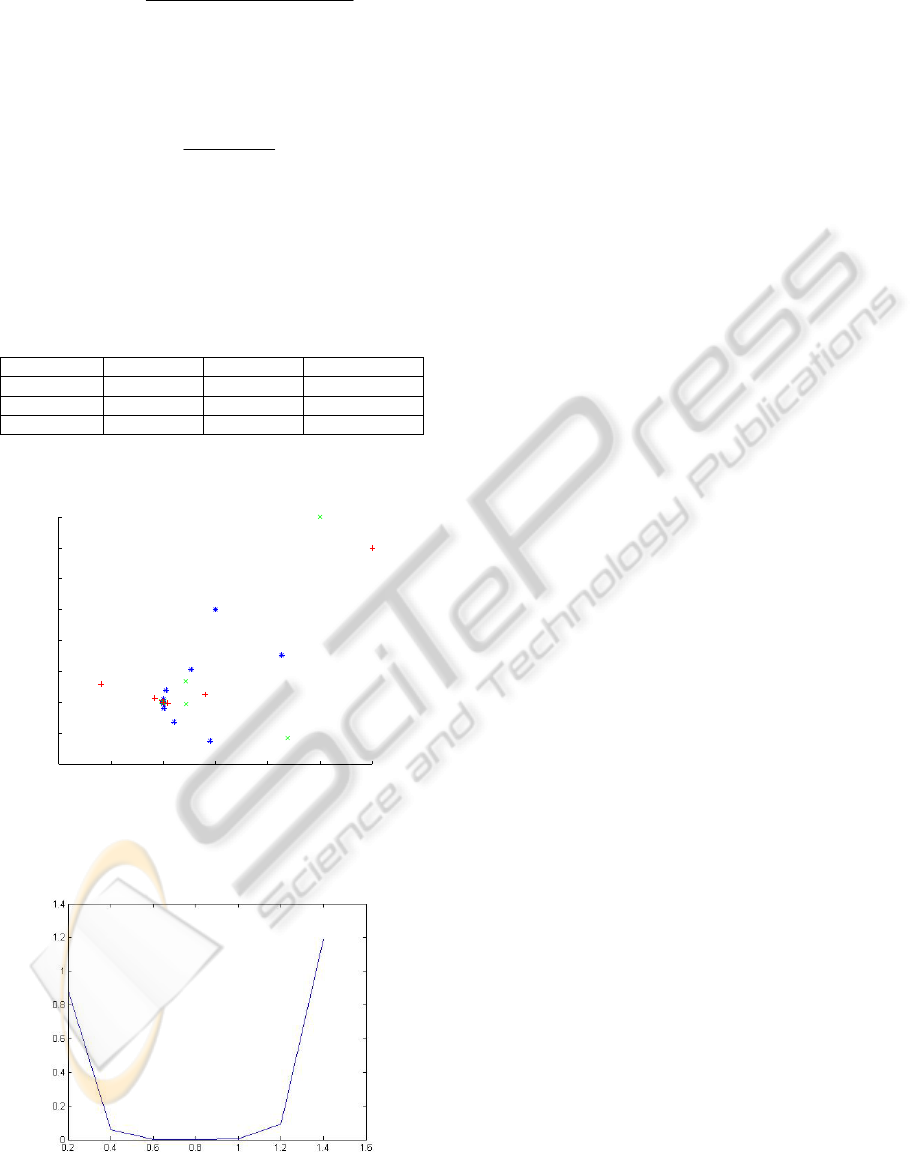
The relation between the convergence precision
and step size is shown in Figure 5.
Figure 5: Convergence precision vs. step size.
An optimum step size is in the range 0.6 – 1;
outside this range, the convergence precision
decreases.
6 CONCLUSIONS
This paper capitalizes on recent results showing
convergence of optimization in distributed agent
applications. The optimization is based on
establishing weights between agents, such that a
weighted recursive computation shown in formula
(14) gives a shared optimal resource allocation. This
approach is appropriate for cooperative multi-robot
system.
The paper’s contribution is to demonstrate that a
natural approach to compute a “distance” (the
weight) among agents that exchange ontologies
among them is the degree of shared ontologies the
agents are using at the current computation step.
This allows both numerical and symbolical
ontological concepts to be used by set-theoretic
similarity measures.
REFERENCES
Debenham, J, Sierra, C., 2008. Unifying trust, honour and
reliability. In 2
nd
IEEE Int’l Conf.on Digital
Ecosystems and Technologies, 2008, pp. 470-475.
Fletcher, R., 2003. Practical Methods of Optimization.
Wiley. UK. 2
nd
edition.
Min, X., Luo, Z., Qianxing, X., 2009.
Semantic Similarity
between Concepts Based on OWL Ontologies. In 2
nd
Int’l Workshop on Knowledge Discovery and Data
Mining, 2009, Moscow, pp. 749-752.
Nedic, A., Ozdaglar, A., 2009. Distributed Subgradient
Methods for Multi-Agent Optimization. In IEEE
Transactions On Automatic Control, Vol. 54, No. 1,
pp. 48-61.
Noy, N.F., McGuinness, D.L., 2001. Ontology
Development 101: A Guide to Creating Your First
Ontology. Stanford Knowledge Systems Laboratory
Technical Report KSL-01-05 and Stanford Medical
Informatics Technical Report SMI-2001-0880.
Shor, N.Z., Kiwiel, K.C., Ruszcaynski, A., 1985.
Minimization Methods for Non-differentiable
Functions. Springer-Verlag. New York, USA.
Văcariu, L., Chintoanu, M., Lazea, G., Creţ, O., 2007.
Communication at Ontological Level in Cooperative
Mobile Robots System. In Proceedings of the 4th
International Conference on Informatics in Control,
Automation and Robotics, ICINCO 2007, May 9-12,
2007, Angers, France, pp. 455-460.
DISTRIBUTED OPTIMIZATION BY WEIGHTED ONTOLOGIES IN MOBILE ROBOT SYSTEMS
185
