CLASSIFICATION OF POWER QUALITY DISTURBANCES VIA

HIGHER-ORDER STATISTICS AND SELF-ORGANIZING NEURAL

NETWORKS

Juan Jos´e Gonz´alez de la Rosa, Jos´e Carlos Palomares, Agust´ın Ag¨uera

Univ. C´adiz, Electronics Area, Research Group PAIDI-TIC-168

EPSA, Av. Ram´on Puyol S/N, E-11202-Algeciras-C´adiz, Spain

Antonio Moreno Mu˜noz

Univ. C´ordoba, Electronics Area, Research Group PAIDI-TIC-168

Campus Rabanales, Ed. L. Da Vinci, E-14071-C´ordoba, Spain

Keywords: Higher-Order Statistics (HOS), Neural classiﬁers, Power-quality.

Abstract: This work renders the classiﬁcation of Power Quality (PQ) disturbances using fourth-order sliding cumulants’

maxima as the key feature. These estimators are calculated over high-pass ﬁltered real-life signals, to avoid

the low-frequency 50-Hz sinusoid. Four types of electrical AC supply anomalies constitute the starting grid of

a competitive layer performance, which manages to classify 90 signals within a 2D-space (whose coordinates

are the minima and the maxima of the sliding cumulants calculated over each register). Four clusters have

been clearly identiﬁed via the competitive network, each of which corresponds to a type of anomaly. Then, a

Self-Organizing Network is conceived in order to guess additional classes in the feature space. Results suggest

the idea of two additional sets of signals, which are more related to the degree of signals’ degeneration than to

real new groups of anomalies. We collaterally conclude the need of additional features to face the problem of

subclass division. The experience sets the foundations of an automatic procedure for PQ event classiﬁcation.

1 INTRODUCTION

Power Quality (PQ) analysis is becoming a key factor

for the economy because equipment is highly sensi-

tive to the power line signal’s imperfections (Moreno

and et al, 2007; IE3, 1995b). As a consequence, mal-

functioning not only has to be detected, but also pre-

dicted and diagnosed, to identify the cause and pre-

vent the system from a similar shock. This is reﬂected

a posteriori in an increase in the amount and qual-

ity of the industrial production. The solution for a

PQ problem implies the acquisition and monitoring

of long data records from the energy distribution sys-

tem, along with a detection and classiﬁcation strat-

egy, which allows the identiﬁcation of the cause of

these voltage anomalies. These perturbations can be

considered as non-stationary transients, so it is nec-

essary a battery of observations to obtain a reliable

characterization. The goal of the signal processing

is to get a feature vector from the target data, which

constitute the input to the computational intelligence

modulus, with the task of classiﬁcation. Traditional

measurement algorithms are mainly based in spec-

tral analysis and wavelet transforms. Complementary

second-order methods are based on the independence

of the spectral components and the evolution of the

spectrum in the time domain. Others are threshold-

based functions, linear classiﬁers and Bayesian net-

works (De la Rosa et al., 2009, ).

Recent works are bringing a higher-order statis-

tics (HOS) based strategy, dealing with PQ analysis

(De la Rosa et al., 2007;

Omer Nezih Gerek and Ece,

2006, ), and other ﬁelds of Technology (De la Rosa

et al., 2004; De la Rosa et al., 2008, ). They are based

in the following argument. Without perturbation, the

50-Hz of the voltage waveform exhibits a Gaussian

behavior. Deviations can be detected and character-

ized via HOS; non-Gaussian processes need at least

and 4

-order statistical characterization in order

to be characterized, because 2

-order moments and

cumulants could be not capable of differentiate non-

Gaussian events.

Concretely, the problem of differentiating be-

tween a transient of long duration named oscillatory

183

José González de la Rosa J., Carlos Palomares J., Agüera A. and Moreno Muñoz A. (2010).

CLASSIFICATION OF POWER QUALITY DISTURBANCES VIA HIGHER-ORDER STATISTICS AND SELF-ORGANIZING NEURAL NETWORKS.

In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 183-190

DOI: 10.5220/0002915101830190

 SciTePress

(within a signal period) and a short duration transient,

or impulsive transient (25 per cent of a cycle), has

been outcome under controlled conditions in (De la

Rosa et al., 2009, ), and the idea of differentiating

between healthy signals and signals with transients

was pointed out and accomplished in (De la Rosa

and Mu˜noz, 2009, ). This problem was previously

described in (Bollen et al., 2005) and matches HOS

category, in the following sense. The short transient

could also bring the 50-Hz voltage to zero instantly

and, generally affects the sinusoid dramatically. By

the contrary, the long-duration transient could be con-

sidered as a modulating signal (the 50-Hz signal is

the carrier), and is associated to load charges (Bollen

et al., 2005). Similarly, considering the statistical de-

viation from the Gaussian behavior that power dis-

turbances add to the power line, it seems appropri-

ate to launch the task of higher-order classiﬁcation of

more types of electrical anomalies, also considering

the conﬂuence of various perturbations in the same

measurement register.

The contribution of this paper consists of the ap-

plication of fourth-order central cumulants at zero

lags to characterize PQ events in the time-domain

(measuring maxima and minima values of higher-

order cumulant sequences), along with the use of

competitive layer and SOM as the classiﬁcation tools.

Four different sets of signals have been a priori estab-

lished and conﬁrmed using a competitive layer. The

ﬁrst set comprises healthy sine-waves from the power

50 Hz-line. Then, we consider signals with oscil-

latory mono-frequency (long duration) transients of

relatively high amplitude; we also consider for the

second set the signals with harmonics, which dis-

tort the shape of the sine-wave producing a not very

high valued fourth-order cumulant. The third group

gathers features’ anomalies which appeared simulta-

neously in a signal, corresponding to impulsive tran-

sients (of short duration), and/or a weak sag (RMS de-

scent), and/or oscillatory high-amplitude events. Fi-

nally, signals clearly affected by high-amplitude im-

pulsive transients and/or deep sags are contained in

the fourth set. Sets ♯3 and ♯4 may be joined in one,

but signals in set ♯4 are clearly more affected and

probably by only one type of perturbation. On the

other hand, signals belonging to set ♯3 are generally

affected by several anomalies. Consequently, four

classes have been established with the possibility od

upgrading the detection towards 6 clusters.

The paper is structured as follows. The following

Section 2 explains the fundamentals of power quality

monitoring. Higher-Order Statistics are outlined then

in Section 3, to be followed by a summary on compet-

itive layers and self-organizing networks in Section .

Finally, results are presented in Section 5 and conclu-

sions are drawn in Section 6.

2 POWER-QUALITY

CHARACTERIZATION

As more and more electronic equipments enter the

residential areas and business environment, the sub-

jects related to PQ and its relationship to vulnerabil-

ity of installations is becoming an increasing concern

to the users. Particularly has arisen and increased the

need to protect sensitive electronic equipment from

damaging over-voltages. Things like lightning, large

switching loads, non-linear load stresses, inadequate

or incorrect wiring and grounding or accidents in-

volving electric lines, can create problems to sensitive

equipment, if it is designed to operate within narrow

voltage limits, or if it does not incorporate the capa-

bility of ﬁltering ﬂuctuations in the electrical supply

(Bollen et al., 2005; Moreno and et al, 2007; Paul,

2001).

The two main regulated aspects of PQ are the fol-

lowing:

• Technical PQ, which includes: Continuity of sup-

ply or reliability (long interruptions) and Voltage

quality (voltage level variations and voltage dis-

turbances).

• Commercial services associated to the wires (such

as the delay to get connected to the grid, etc.) as

well as commercial services for energy retail to

regulated customers.

Assessment of voltage quality and power distur-

bances involves looking at electromagnetic devia-

tions of the voltage or current from the ideal single-

frequency sine wave of constant amplitude and fre-

quency. A consistent set of deﬁnitions can be found in

(IE3, 1995b). Regulation in European countries pro-

poses to use the standard EN-50160 to deﬁne the volt-

age quality ranges. This norm actually describes the

electricity through the technical characteristics that it

has to fulﬁll to be considered as a compliant prod-

uct. But there are a lot of undeﬁned aspects; besides

the fact that most of the regulator has yet to publish

the technical criteria to measure and control all the

voltage quality characteristics and decide what would

be the penalization. The fact is that the only voltage

quality aspect that is now enforced is the maximum

voltage level variation settled to ± 7 % (which is ac-

tually different to the ±10 % ﬁxed on the EN-50160).

But even this aspect is not yet controlled and there is

not any deﬁned procedure to determine if the limit has

been reached.

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

184

On the other hand, the presence of disturbances

on power distribution also affect the energy efﬁciency

of the system. As far as energy efﬁciency is con-

cerned in a power distribution system, the two dom-

inant factors in PQ are its unbalanced and harmonic

distortion. In an electrical installation when single-

phase loads (especially those with non-linear charac-

teristics), are not evenly and reasonably distributed

among the three-phases of the supply, we are in the

presence of unbalance. Voltage unbalance in a three-

phase system causes three-phase motors to draw un-

balanced current. This phenomenon causes additional

power losses in conductors and motors and can cause

the rotor of a motor to overheat.

Among all categories of electrical disturbances,

the voltage sag (dip) and momentary interruption are

the nemeses of the automated industrial processes.

Voltage sag is commonly deﬁned as any low voltage

event between 10 and 90% of the nominal RMS volt-

age lasting between 0.5 and 60 cycles. Momentary

voltage interruption is any low-voltage event of less

than 10% of the nominal RMS voltage lasting be-

tween 0.5 cycles and 3 seconds. In medium voltage

distribution networks, voltage sags are mainly caused

by power system faults. Fault occurrences elsewhere

can generate voltage sags affecting consumers differ-

ently according to their location in the electrical net-

work. Even though the load current is small compared

to the fault current, the changes in load current dur-

ing and after the fault strongly inﬂuence the voltage

at the equipment terminals. It has been discovered

that the 85% of power supply malfunctions attributed

to poor PQ are caused by voltage sag or interruptions

of fewer than one second duration. Starting large mo-

tors can also generate voltage sags, although usually

not so severe. In comparison with interruptions, volt-

age sags affect a larger number of customers and for

some customers voltage sags may cause extremely se-

rious problems. These can create problems to sen-

sitive equipment if it is designed to operate within

narrow voltage limits, or it does not have adequate

ride-through capabilities to ﬁlter out ﬂuctuations in

the electrical supply.

Over-voltage is an RMS increase in the AC volt-

age, at the power frequency, for durations greater than

a few seconds, and can be the result of a programmed

utility operation, or the effect of an external eventu-

ality (IE3, 1995a). Under normal operating condi-

tions, the steady-state voltage is regulated by the util-

ity within a limits band accepted by the EN-50160.

Deviations from these limits are rare, and the utility

can actuate readily to correct them, if known their oc-

currence, by acting on conventional distribution tech-

nologies, such as tap-changing transformers (Moreno

et al., 2007).

However, under the typical operating conditions

of a power system there is risk of damaging due to

a momentary excess of voltage. Although by them-

selves they would be described as ”abnormal”, it is

possible to distinguish between surges and swells. A

surge is an over-voltage that can reach thousands of

volts, lasting less than one cycle of the power fre-

quency, that is, less than 16 milliseconds. A swell

is longer, up to a few seconds, but does not exceed

about twice the normal line voltage.

Power system surges, based on waveform shapes,

can be classiﬁed into ”oscillatory transients” and ”im-

pulsive transients” (IE3, 1995b; Paul, 2001) and they

are the goal of the present research work. Oscilla-

tory transient surges show a damped oscillation with

a frequency range from 400 Hz to 5 kHz or more. Im-

pulsive transient surges present a fast rise time in the

order of 1 ns-10 µs over the steady state condition of

voltage, current or both, that is unidirectional in po-

larity (primarily either positive or negative), reaching

hardly twice the peak amplitude of the signal. They

are damped quickly, presenting a frequency range

from 4 kHz to 5 MHz, occasionally reaching 30 MHz.

Categorization of electrical transients based on

waveform shapes and their underlying causes (or

events) has been studied in (Bollen et al., 2005), and

a few previous studies (De la Rosa et al., 2007;

Omer

Nezih Gerek and Ece, 2006, ) using HOS for feature

extraction of electrical signals have shown the pos-

sibility of distinguish transients based on details be-

yond the second-order. In a real-life 50-Hz power

line signal, it is very common to ﬁnd these transients.

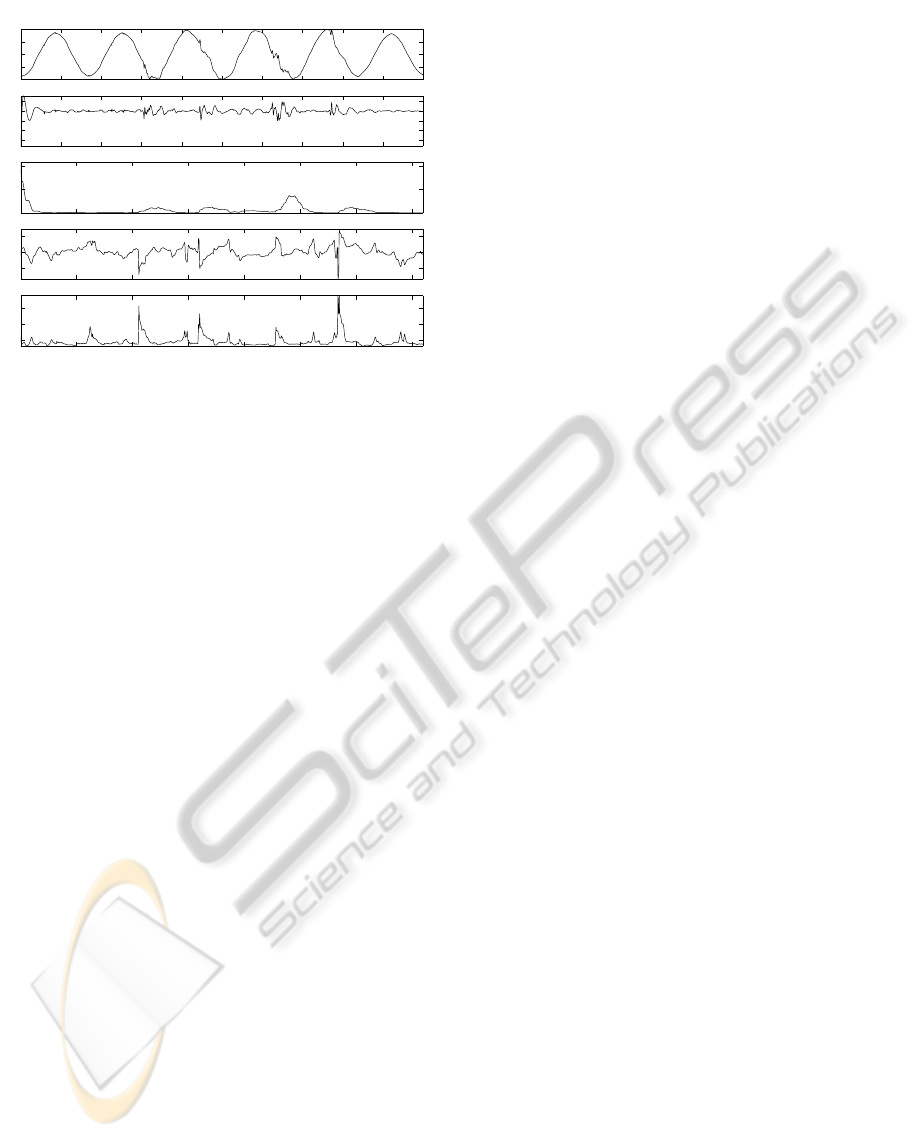
In Fig. 1 we show an example of anomalous signal,

including transients which are not classiﬁed between

short-duration and long-duration. We show the com-

putation of three higher-order time-domain statistics

in order to introduce them qualitatively. The second-

order estimator operates as an increase-of-power de-

tector, showing the bumps associated to the increase

of power, which in turn are associated to the anoma-

lies of the power-line sine wave, but the third and

fourth-order sliding cumulants have to be interpreted

further. The most intuitive procedure is to calculate

their maxima and minima.

Once the foundations of PQ have been settled

down, in the following Section we present higher-

order statistics in the time-domain in order to present

the signal processing tool, along with a basic example

which shows the performance of the statistical esti-

mators which have been used in the computation of

the cumulants. This example also motivates the use

of HOS in time-series characterization.

CLASSIFICATION OF POWER QUALITY DISTURBANCES VIA HIGHER-ORDER STATISTICS AND

SELF-ORGANIZING NEURAL NETWORKS

185

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09

−0.5

0.5

Analysis of several transients

0 0.01 0.02 0.03 0.04 0.05 0.06 0.07 0.08 0.09

−0.6

−0.4

−0.2

0.2

Time(s)

200 400 600 800 1000 1200 1400

0.02

0.04

Second−order sliding cumulants: power bumps

200 400 600 800 1000 1200 1400

−2

Third−order sliding cumulants

200 400 600 800 1000 1200 1400

Number of segment

Fourth−order sliding cumulants

Figure 1: Several transients in the power line 50-Hz sine

wave, and the computation of time-domain statistics. The

signal has been previously normalized and high-pass ﬁl-

tered in order to remain with the transients.

3 HIGHER-ORDER STATISTICS

Higher-order cumulants are used to infer new proper-

ties about the data of non-Gaussian processes (De la

Rosa et al., 2004, ). In multiple-signal processing

it is very common to deﬁne the combinational rela-

tionship among the cumulants of r stochastic signals,

}

i∈[1,r]

, and their moments of order p,p ≤ r, given

by using the Leonov-Shiryaev formula (Nikias and

Mendel, 1993; Mendel, 1991)

Cum(x

,...,x

) =

∑

(−1)

p−1

· (p− 1)!· E{

∏

i∈s

}

· E{

∏

i∈s

}·· ·E{

∏

i∈s

(1)

where the addition operator is extended over all

the partitions, like one of the form (s

,.. . ,s

p = 1, 2,· ·· ,r; and (1 ≤ i ≤ p ≤ r); being s

a set be-

longing to a partition of order p, of the set of integers

1,...,r.

Let {x(t)} be an rth-order stationary random real-

valued process. The rth-order cumulant is deﬁned as

the joint rth-order cumulant of the random variables

x(t), x(t+τ

),..., x(t+τ

r−1

r,x

(τ

,τ

,.. . ,τ

r−1

)

= Cum[x(t),x(t + τ

),... ,x(t + τ

r−1

)]

(2)

The second-, third- and fourth-order cumulants of

zero-mean x(t) can be expressed via:

2,x

(τ) = E{x(t) · x(t + τ)} (3a)

3,x

(τ

,τ

) = E{x(t) · x(t + τ

) · x(t + τ

)} (3b)

4,x

(τ

,τ

)

= E{x(t)· x(t + τ

) · x(t + τ

)}

−C

2,x

(τ

2,x

(τ

− τ

)

−C

2,x

(τ

2,x

(τ

− τ

)

−C

2,x

(τ

2,x

(τ

− τ

)

(3c)

By putting τ

= τ

= 0 in Eq. (3), we obtain

2,x

= E{x

(t)} = C

2,x

(0) (4a)

3,x

= E{x

(t)} = C

3,x

(0,0) (4b)

4,x

= E{x

(t)} − 3(γ

2,x

)

= C

4,x

(0,0, 0) (4c)

The expressions in Eq. (4) are measurements of

the variance, skewness and kurtosis of the distribu-

tion in terms of cumulants at zero lags (the central

cumulants).

Normalized kurtosis and skewness are deﬁned as

4,x

/(γ

2,x

)

and γ

3,x

/(γ

2,x

)

3/2

, respectively. We will

use and refer to normalized quantities because they

are shift and scale invariant. If x(t) is symmetrically

distributed, its skewness is necessarily zero (but not

vice versa); if x(t) is Gaussian distributed, its kurtosis

is necessarily zero (but not vice versa). In the exper-

imental section, results are obtained by using sliding

cumulants, i.d. a moving window in the time domain

over which to compute the each cumulant.

To show the relevance of HOS an illustrative ex-

ample is prepared. Four noise processes: Gaussian;

uniform; exponential and Laplacian, previously cat-

alogued in, and indistinguishable from the second-

order perspective, are presented in this subsection

in order to illustrate the importance of introducing

higher-order cumulants. The 4th-order cumulants are

computed according to the estimate given in (De la

Rosa et al., 2009, ). We consider a 2048-point sam-

ple register for each random set of data. The four

identical autocorrelation sequences contrast to the

fourth-order ones, where substantial differences are

observed, specially those corresponding to zero time

lags. This can be seen in Fig. 2, where the 4th-order

cumulant sequences are depicted. The theoretical val-

ues of the cumulants at zero time-lag are: 0 (Gaus-

sian), -1 (uniform), 6 (Exponential), 12 (Laplacian).

The difference between the theoretical and the exper-

imental value is due to the lack of averaging (only one

sample register is consider). The convergency of the

estimate is assured.

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

186

−20 −15 −10 −5 0 5 10 15 20

−0.1

0.1

Gaussian

4,x

(τ

,0,0); τ

=τ

−20 −15 −10 −5 0 5 10 15 20

−1.5

−1

−0.5

Uniform

−20 −15 −10 −5 0 5 10 15 20

Exponential

−20 −15 −10 −5 0 5 10 15 20

−5

Laplacian

−0.075

−1.16

5.55

10.78

Figure 2: 4th-order cumulant sequences for the four noise

processes. Sample values at zero time lag are included in

each sub-ﬁgure.

4 COMPETITIVE LAYERS AND

SELF-ORGANIZING MAPS

In a competitive layer neurons distribute themselves

to recognize frequently presented input vectors. The

competitive transfer function accepts a net input vec-

tor p for a layer (each neuron competes to respond to

p) and returns neuron outputs of 0 for all neurons ex-

cept for the winner, the one associated with the most

positive element of net input. If all biases are 0, then

the neuron whose weight vector is closest to the input

vector has the least negative net input and, therefore,

wins the competition to output a 1.

The winning neuron will move closer to the input,

after this has been presented. The weights of the win-

ning neuron are adjusted with the Kohonen learning

rule (0.9 in the present case). Supposing that the ith-

neuron wins, the elements of the ith-row of the input

weight matrix (IW) are adjusted as shown in Eq. (5):

1,1

(q) = IW

1,1

(q− 1)+ α

p(q) − IW

1,1

(q− 1)

(5)

where p is the input vector, q is the time instant,

and α is the learning rate. The neuron whose weight

vector was closest to the input vector is updated to

be even closer. The result is that the winning neuron

is more likely to win the competition the next time

a similar input is presented. As more inputs are pre-

sented, each neuron in the layer closest to a group of

input vectors soon adjusts its weights toward those in-

puts. Eventually, if there are enough neurons, every

cluster of similar input vectors will have a neuron that

outputs 1 when a vector in the cluster is presented,

while outputting a 0 at all other times. Thus, the com-

petitive network learns to categorize the input vectors.

Self-Organizing Maps (SOM) learn to classify

feature input vectors according to how they are

groupedin the input space. SOM differ from competi-

tive layers in that neighbor-neurons learn to recognize

neighboring sections of the input space. Thus, SOM

learn both the distribution (as do competitive layers)

and topology of the input vectors they are trained on.

Consequently, instead of updating only the winning

neuron, all neurons in its neighborhood are updated

using the Kohonen rule. The neurons in the layer of

a SOM are arranged originally in physical positions

according to a topology function. A distance function

allows the calculation of the distances between neu-

rons. Thus, for the ith neighboring neuron, in the qth

instant, we have the weight vector w, in Eq. (6):

(q) = w

(q− 1) + α[p(q) − w

(q− 1)]. (6)

Thus, when a vector is presented, the weights of

the winning neuron and its closest neighbors move to-

ward. Consequently, after many presentations, neigh-

boring neurons will have learned vectors similar to

each other.

5 EXPERIMENTAL RESULTS

As conveyed in previous sections, the experiment

comprises two phases. The feature extraction, and

ﬁrst stage, is based on the calculation of the max-

ima and minima of the 4th-order central cumulants

at zero lags for each data recording; i.d., each signal

is characterized in a 2-D space by a vector, whose co-

ordinates correspond to the local maxima and min-

ima of the 4

-order central cumulants. A number

of 90 different measured power-line signals were se-

lected, containing different PQ anomalies. Secondly,

the classiﬁcation stage (on the 90 feature vectors)

is based on the application of ANN as classiﬁcation

tools in a twofold frame. The mission of the competi-

tive layer consists of conﬁrming the existence of four

different sets of signals’ classes (a priori established

in the research). Additionally, the SOM network is

conceived to guess additional possible classes and, in

case of ﬁnding out more, determine their nature and

relationship with the ﬁrstly proposed four groups of

features.

Each cumulant is computed over 50 points; this

window’s length (50 points) has been selected nei-

ther to be so long to cover the whole signal nor to be

very short to loose information. The algorithm calcu-

lates the cumulant over 50 points, and then it jumps to

the following starting point (next 50-point overlapped

CLASSIFICATION OF POWER QUALITY DISTURBANCES VIA HIGHER-ORDER STATISTICS AND

SELF-ORGANIZING NEURAL NETWORKS

187

group); as a consequencewe have 98 per cent overlap-

ping sliding windows (49/50=0.98). Then each com-

putation over a window (called a segment) outputs a

-order cumulant.

Besides, each 4th-order cumulant, Cum

n,x

[i], as-

sociated to the ith computation segment has been nor-

malized by (Cum

2,x

[i])

, in order to obtain categoriza-

tion results associated to the shape of the sliding cu-

mulants. This gives a real statistical characterization.

If the cumulants are not normalized, the maxima and

minima also gather information regarding the abso-

lute value of the cumulants. The higher-order (n>2)

normalized cumulants are the skewness and the kur-

tosis.

Before the computation of the biased cumulants,

two pre-processing actions have been performed over

the sample signals. First, they have been normalized

because they exhibit very different-in-magnitudevolt-

age levels. This disparity of voltage levels cannot in-

ﬂuence the results of the categorization. Secondly, a

high-pass digital ﬁlter (5th-order Butterworth model

with a characteristic frequency of 150 Hz) eliminates

the low frequency components which are not the tar-

gets of the experiment.

Once ﬁltered, each signal contains one or more

types of PQ events. Four different sets of signals

have been a priori settled down empirically, based

on the qualitative human knowledge, and then con-

ﬁrmed using a competitive layer. The ﬁrst set com-

prises healthy sine-waves from the power 50 Hz-line.

Then, we consider signals with oscillatory mono-

frequency (long duration) transients of relatively high

amplitude; we also consider for the second set signals

with harmonics, which distort the shape of the sine-

wave producing a not very high valued fourth-order

cumulant. The third group gathers features’ anoma-

lies which appeared simultaneously in a signal, corre-

sponding to impulsive transients (of short duration),

and/or a weak sag (RMS descent), and/or oscillatory

high-amplitude events. Finally, signals clearly af-

fected by high-amplitude impulsive transients and/or

deep sags are contained in the fourth set. Sets ♯3

and ♯4 may be joined in one, but signals in set ♯4 are

clearly more affected and probably by only one type

of perturbation. On the other hand, signals belonging

to set ♯3 are generally affected by several anomalies.

Consequently, four classes have been established with

the possibility of upgrading the detection towards 6

clusters. The limits for the four classes’ intervals, in

units of cumulants maxima are: [0,7], [7,12], [12,20],

[20,40]. These classes can be appreciated in Fig. 3, in

the upper sub-graph, for the competitive layer train-

ing results. The lower subgraph in Fig. 3, shows

the results of applying the SOM network and can be

seen the shifting phenomenon that occurs for the ﬁ-

nal weights vector after the training stage of the NNT

over 50 epochs. This result conveys the idea of the

SOM network used to reﬁne the classiﬁcation, more

than performing the coarse sub-divisionin anomalies’

subclasses.

0 5 10 15 20 25 30 35 40

−1.8

−1.75

−1.7

−1.65

−1.6

−1.55

−1.5

−1.45

Cumulant maxima

Cumulant minima

Competitive learning. Clusters: 4

−order cumulants

:measured vector

:initial neuron weight vector

:final neuron weight vector

0 5 10 15 20 25 30 35 40

−1.8

−1.75

−1.7

−1.65

−1.6

−1.55

−1.5

−1.45

Cumulant maxima

Cumulant minima

Self−Organizing Map. Clusters: 4

−order cumulants

:measured vector

:initial neuron weight vector

:final neuron weight vector

Figure 3: Four clusters for 4 types of signals. A randtop

2 × 2 topology has been selected over 50 epochs training.

Upper graph: competitive layer performance. Down graph:

SOM performance.

The separation between classes (inter-class dis-

tance) is well deﬁned in the 2-D feature graph for the

competitive layer. Consequently, the four types of PQ

events are clustered. The correct conﬁguration of the

clusters is corroborated during the simulation of the

neural network, in which we have obtained an approx-

imate classiﬁcation accuracy of 95 percent. During

the simulation, new signals (randomly selected from

our data base) were processed using this methodol-

ogy. The accuracy of the classiﬁcation results in-

creases with the number of data. To evaluate the con-

ﬁdence of the statistics a signiﬁcance test has been

conducted. As a result, the number of measurements

is signiﬁcantly correct.

An attempt to classify signals according a 6-

cluster pattern has been developed. The limits for the

four classes’ intervals, in units of cumulants maxima

are: [0,2], [2,7], [7,12], [12,20], [20,30], [30,40]. The

new proposed intervals (added to the four classes pro-

posal) are related to graded anomalies. The training

results are displayed in Fig. 4, conveyingthe idea that,

new classes are not really new anomalies.

In fact, despite the fact that the competitive layer

manages to classify the signals into 6 classes (we

force it), when we apply SOM networks, due to the in-

ﬂuence of the close neighbor neurons, the ﬁnal weight

vectors are shifted or moved to new positions, de-

pending on the geometry of the network (rand-to,

hex-top). This clearly conﬁrms the idea of a graded

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

188

0 5 10 15 20 25 30 35 40

−1.8

−1.7

−1.6

−1.5

Cumulant minima

Competitive learning. Clusters: 4

−order cumulants

0 5 10 15 20 25 30 35 40

−1.8

−1.7

−1.6

−1.5

Cumulant minima

SOM−randtop. Clusters: 4

−order cumulants

0 5 10 15 20 25 30 35 40

−1.8

−1.7

−1.6

−1.5

Cumulant maxima

Cumulant minima

SOM−hextop. Clusters: 4

−order cumulants

Figure 4: Six clusters for 6 possible types of signals after 50

epochs training. A 2 × 3 topology has been selected. Upper

graph: competitive layer performance. Middle graph: SOM

performance for a rand-top topology. Down graph: SOM

performance for an hex-top topology.

anomaly, because the weight vectors are not located

in the same position for both types of network’s ge-

ometry.

6 CONCLUSIONS

In this paper an automatic procedure to classify

electrical PQ anomalies has been proposed. The

method comprises two stages. The ﬁrst includes pre-

processing (normalizing and ﬁltering) and outputs the

2-D feature vectors, each of which coordinate cor-

responds to the maximum and minimum of the cen-

tral 4th-order cumulants. The second stage is based

in computational intelligence and uses a competitive

layer to conﬁrm the existence of 4 classes, related

to the different groups of anomalies. Then a SOM

network conﬁrms that newly added classes (proposed

empirically) are not really new. New sub-divisions

are related to degree of the degree of the anomaly.

The geometry of the SOM network conﬁrm this fact,

moving the ﬁnal weight vectors to different positions.

Future work is designed to deal with a great number

of signals (more than 90), trying to guess more classes

with the aim of generalizing the method.

ACKNOWLEDGEMENTS

The authors would like to thank the Spanish Min-

istry of Science and Innovation for funding the re-

search project TEC2009-08988. Our unforgettable

thanks to the trust we have from the Andalusian Gov-

ernment for funding the Research Unit PAIDI-TIC-

168 in Computational Instrumentation and Industrial

Electronics.

REFERENCES

(1995a). IEEE Guide for service to equipment sensitive

to momentary voltage disturbances. Technical Report

IEEE Std. 1250-1995, The Institute of Electrical and

Electronics Engineers, Inc.

(1995b). IEEE Recommended practice for monitoring

electric power quality. Technical Report IEEE Std.

1159-1995, The Institute of Electrical and Electronics

Engineers, Inc.

Bollen, M. H. J., Styvaktakis, E., and Gu, I. Y.-H.

(2005). Categorization and analysis of power sys-

tem transients. IEEE Transactions on Power Delivery,

20(3):105–118.

Mendel, J. M. (1991). Tutorial on higher-order statistics

(spectra) in signal processing and system theory: The-

oretical results and some applications. Proceedings of

the IEEE, 79(3):278–305.

Moreno, A., Flores, J., Oterino, D., and De la Rosa, J.

J. G. (2007). Power line conditioner based on ca pwm

chopper. In ISIE 2007, Proceedings of the 2007 IEEE

International Symposium on Industrial Electronics,

pages 2454–2456, June 2007.

Moreno, A. and et al (2007). Mitigation Technologies in a

Distributed Environment. Power Systems. Springer-

Verlag, 1 edition.

Nikias, C. L. and Mendel, J. M. (1993). Signal process-

ing with higher-order spectra. IEEE Signal Processing

Magazine, pages 10–37.

Omer Nezih Gerek and Ece, D. G. (2006). Power-

quality event analysis using higher order cumulants

and quadratic classiﬁers. IEEE Transactions on Power

Delivery, 21(2):883–889.

Paul, D. (2001). Low-voltage power system surge overvolt-

age protection. IEEE Transactions on Industry Appli-

cations, 37(1):223–229.

De la Rosa, J. J. G., Lloret, I., Puntonet, C. G., and G´orriz,

J. M. (2004). Higher-order statistics to detect and

characterise termite emissions. Electronics Letters,

40(20):1316–1317. Ultrasonics.

De la Rosa, J. J. G., Lloret, I., Puntonet, C. G., Piotrkowski,

R., and Moreno, A. (2008). Higher-order spectra mea-

surement techniques of termite emissions. a charac-

terization framework. Measurement (Ed. Elsevier),

41(1):105–118. Available online 13 October 2006.

De la Rosa, J. J. G., Moreno, A., and Puntonet, C. G. (2007).

A practical review on higher-order statistics interpre-

tation. application to electrical transients characteri-

zation. Dynamics of continous discrete and Impul-

sive Systems-Series B: Applications and Algorithms,

14(4):1577–1582.

CLASSIFICATION OF POWER QUALITY DISTURBANCES VIA HIGHER-ORDER STATISTICS AND

SELF-ORGANIZING NEURAL NETWORKS

189

De la Rosa, J. J. G. and Mu˜noz, A. M. (2009). Higher-

order characterization of power quality transients

and their classiﬁcation using competitive layers.

Przega¸d Elektrotechniczny-Electrical Review, 10(Is-

sue 85):284–289.

De la Rosa, J. J. G., Mu˜noz, A. M., Gallego, A., Pi-

otrkowski, R., and Castro, E. (2009). Higher-order

characterization of power quality transients and their

classiﬁcation using competitive layers. Measurement

(Ed. Elsevier), 42(Issue 3):478–484.

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

190