ON REAL-TIME WHOLE-BODY HUMAN TO HUMANOID MOTION

TRANSFER

Francisco-Javier Montecillo-Puente, Manish N. Sreenivasa and Jean-Paul Laumond

CNRS, LAAS, 7 avenue du colonel Roche, F-31077 Toulouse, France

Universit

e de Toulouse, UPS, INSA, INP, ISAE, LAAS, F-31077 Toulouse, France

Keywords:

Humanoids, HRP2, Human motion, Inverse kinematics, Neuroscience.

Abstract:

We present a framework for online imitation of human motion by the humanoid robot HRP-2. We introduce a

representation of human motion, the Humanoid-Normalized model, and a Center of Mass (CoM) anticipation

model to prepare the robot in case the human lifts his/her foot. Our proposed motion representation codiﬁes

operational space and geometric information. Whole body robot motion is computed using a task-based prior-

itized inverse kinematics solver. By setting the human motion model as the target, and giving the maintenance

of robot CoM a high priority, we can achieve a large range of motion imitation. We present two scenarios

of motion imitation, ﬁrst where the humanoid mimics a dancing motion of the human, and second where it

balances on one foot. Our results show that we can effectively transfer a large range of motion from the human

to the humanoid. We also evaluate the tracking errors between the original and imitated motion, and consider

the restrictions on the range of transferable human motions using this approach.

1 INTRODUCTION

Since the inception of humanoid robots several ap-

proaches have been developed, aiming at enabling au-

tonomous and intelligent behavior of the robot. The

general goal behind this idea is to develop humanoids

that, in the natural environment of the humans and

being among humans, can exhibit complex behavior.

The humanoid and the human share a common an-

thropomorphic structure, and recent studies have ex-

ploited this to directly transfer motion from humans to

humanoids. However, several obstacles imped the di-

rect transfer of motion like technological incompati-

bility of the humanoid robot, fragility, slow (relative

to human) motion speed, as well as a limited range of

motion.

There are several ways to approach the motion

transfer problem. In computer graphics, studies have

looked at “motion retargeting”, where human motion

is transferred from one virtual actor to another (Mul-

ton et al., 2008)(Chois and Ko, 2000). Machine learn-

ing approaches have also been developed to gener-

ate humanoid motion by observing and learning from

a human teacher (Schaal et al., 2003) (Shon et al.,

2005) (Takano et al., 2007). Another method is to

optimize the recorded human motion while consid-

ering humanoid kinematics and dynamics (Suleiman

Figure 1: Picture of a human performer extending a hand-

shake and the humanoid robot HRP-2 imitating the gesture.

HRP-2 is a 30 Dof, 58 kg, 1.54 m tall humanoid robot man-

ufactured by Kawada Industries, Japan. The human motion

was tracked using reﬂective motion markers and transferred

in real-time to the humanoid.

et al., 2008) (Ruchanurucks et al., 2006). For our

purpose we broadly classify motion imitation studies

into ofﬂine and online methods. Ofﬂine methods have

the advantage of having ample processing time and

hence the human motion can be modiﬁed to ﬁt the

humanoid’s limitations. While this allows for gen-

Montecillo-Puente F., N. Sreenivasa M. and Laumond J. (2010).

ON REAL-TIME WHOLE-BODY HUMAN TO HUMANOID MOTION TRANSFER.

In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 22-31

DOI: 10.5220/0002915300220031

 SciTePress

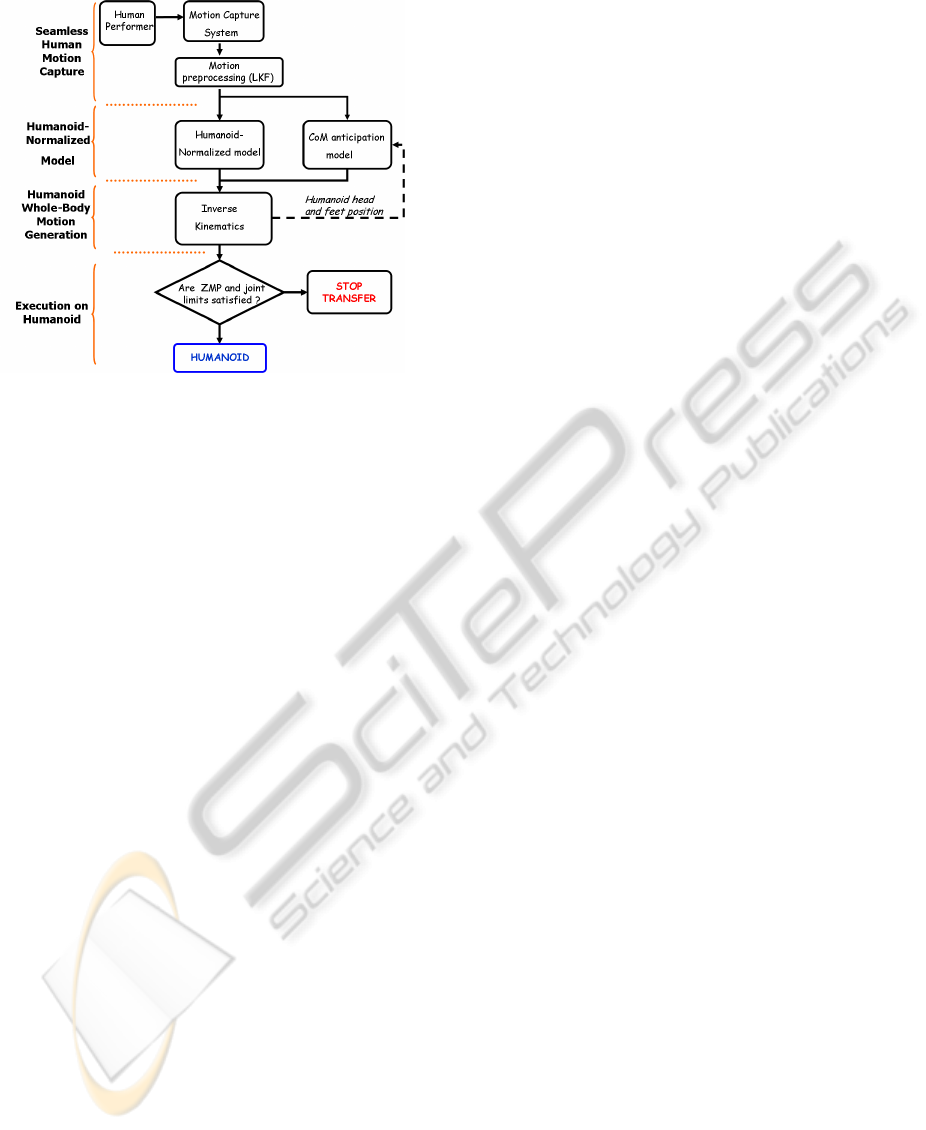
Figure 2: Organization of the algorithm to enable real-time

motion transfer from the human performer to the humanoid

robot.

eration of smooth and optimized motion of the hu-

manoid, these solutions can rarely be applied to on-

line motion transfer, often due to computational de-

lays during the optimization stage. Thus, online trans-

fer of human motion to a humanoid robot provides a

very different set of challenges compared to its ofﬂine

counterpart, and has been the focus of recent research

(Dariush et al., 2008a) (Dariush et al., 2008b) (Ya-

mane and Hodgins, 2009).

We explore this aspect of real-time human-

humanoid motion transfer by developing a framework

that allows us to transfer a large range of human mo-

tions to the humanoid, including balancing on one

foot. The challenges in this task include reliably

recording human motion, morphing the human data

such that it can be applied on a humanoid of a differ-

ent size and joint structure, and, generating the result-

ing humanoid motion in real-time while maintaining

balance.

1.1 Literature Review

1.1.1 Ofﬂine Motion Transfer

First we examine the work by Nakaoka et. al in

2005 (Nakaoka et al., 2005a), that enabled the hu-

manoid robot HRP2 to execute the famous and vi-

sually striking, traditional Aizu-Bandaisan Japanese

dance. Upper body motion for the HRP1s robot was

generated using motion capture markers on human

dancers and inverse kinematics. The leg motion of the

dancers was analyzed and extracted as motion prim-

itives (Nakaoka et al., 2005b). The upper and lower

body motions were then coupled and modiﬁed such

that the robot motion satisﬁed the dynamic stability

criteria, the Zero Moment Point (ZMP) (Vukobra-

tovic and Stepanenko, 1972). This method was imple-

mented ofﬂine and required several runs of the analyt-

ical process to reach a viable solution. However, this

method is not be easily applicable to a range of mo-

tions due to the extensive tuning and re-calculation re-

quired. As a more general framework, Ude et. al pro-

posed to solve a large scale optimization problem to

generate joint trajectories for a DB robot (Ude et al.,

2004). Joint angle trajectories of human motion were

computed by embedding a scalable kinematic struc-

ture to the human body motion. This was also solved

as an ofﬂine process because of the optimization com-

putational load. Robot balance was not taken into

consideration.

In the study by Ruchanurucks et al. (Ruchanu-

rucks et al., 2006), a non-linear optimization process

was solved subject to joint limits, autocollision, ve-

locity limits and force limits constraints. To increase

the convergence speed they parametrized the motion

by B-splines. In Suleiman et. al (Suleiman et al.,

2008), ﬁrst the joint motion data was scaled into the

humanoid robot’s joints. Then, an optimization prob-

lem was solved to ﬁt this motion to the robot structure

and its physical limits, keeping in mind the analyti-

cal gradient of the dynamic model. Among other ap-

proaches, studies have also used machine learning al-

gorithms to imitate human motion (Shon et al., 2005).

The idea here was to generate a low dimensional la-

tent space to map a model variable from the robot

motion to human motion, and vice-versa. In order

to generate the ﬁnal stable motion, extensive training

was required using pairs of human and robot motion.

In most of these studies the humanoid is con-

strained to maintain both its feet on the ground. Even

in the approaches that allowed feet motion, for exam-

ple (Suleiman et al., 2008) and (Ruchanurucks et al.,

2006), the timing of the foot lift-off has to be prede-

ﬁned which results in a rigid range of motion.

1.1.2 Online Methods

In the context of online transfer of human motion to

humanoid robots or even virtual avatars in animation,

the means used to capture human motion plays a very

important role. One way is the use of motion capture

technology. These systems represent human motion

by directly tracking the position of infra-red markers

attached to the human body or attaching a skeleton

to these markers. However, some recent studies have

also implemented markerless tracking where human

motion is reconstructed by using video cameras.

First, we consider the study by Dariush et al. (Dar-

iush et al., 2008b), where the authors developed a

ON REAL-TIME WHOLE-BODY HUMAN TO HUMANOID MOTION TRANSFER

methodology to retarget human motion data to the hu-

manoid robot ASIMO. Human motion was captured

using a markerless pose tracking system. Here upper

body motion was considered by mapping the carte-

sian positions of the waist, wrists, elbows, shoulder

and neck. The corresponding joint motion on the

humanoid was calculated using inverse kinematics,

while respecting the individual joint limits. In this

case, a seperate balance controller was used to move

the legs in order to compensate for the retargeted mo-

tion of the upper body. In a later study, the authors

used a learning approach to pre-generate knowledge

about a number of human postures (Dariush et al.,

2008a). During the actual motion retargeting, head

and torso motion was monitored and the template

closest from the ones learned was assigned. The arms

were analyzed as 3D blobs and their position esti-

mated. From this data the 3D features for head, shoul-

der, waist, elbows and wrists were localized. Using

inverse kinematics and the balance controller, the mo-

tion was then played on the humanoid robot.

Using a different approach, Yamane et al. (Ya-

mane and Hodgins, 2009), simultaneously tracked

motion capture data using a balance controller and a

tracking controller. Tha balance controller was a lin-

ear quadratic regulator designed for an inverted pen-

dulum model. The tracking controller computed joint

torques to minimize the difference from the desired

human capture data while considering full-body dy-

namics. The resulting motion was retargeted on the

humanoid in simulation.

1.2 Our Contribution

We present an alternative way to transfer human

motion data to our humanoid robot HRP2.

• Taking inspiration from computer animation

studies we extended the idea of the normalized

skeleton (Multon et al., 2008) and developed a

“Humanoid-Normalized model” on which ﬁltered

motion capture data can be retargeted online. To

do this we ﬁrst devise a method to reliably record

human motion by using Kalman ﬁlters to ﬁll gaps

(due to occlusions) in capture data. Rather than

directly using cartesian positions like in (Dariush

et al., 2008a) (Dariush et al., 2008b), or joint angles

(Yamane and Hodgins, 2009), we also encode the

orientation of the postures by attaching virtual planes

to sets of human motion marker points. These virtual

planes deﬁne the orientation of the important joints in

the human, like the head, chest, arms and waist. We

propose a Humanoid-Normalized model that consists

of a combination of the positions of the extremities

and the normals to the virtual planes. The motion of

this model is used to drive the humanoid robot via a

task based inverse kinematics solver.

• In order to achieve single foot support phases

we also introduce the original idea of an anticipation

model, motivated by results in human neuroscience.

This model serves the purpose of preparing the

humanoid to stand on one foot by taking into ac-

count previous motion of the human head, and the

humanoid’s Center of Mass (CoM). Figure 2 shows

the organization of the overall algorithm.

We evaluate the results from our experiments and

compare them to those reported in literature. In the

following sections we describe in detail 1) The cap-

ture of human motion capture data, 2) Application to

the Humanoid-Normalized model, 3) Generating hu-

manoid motion using inverse kinematics 4) The CoM

Anticipation model 5) Experiments on our humanoid

robot, HRP2 and ﬁnally 6) Discussion of our results

as well as future perspectives.

2 SEAMLESS HUMAN MOTION

CAPTURE

Human motion was recorded in a tracking hall

equipped with 10 infra-red tracking cameras (Mo-

tionAnalysis, CA, USA). The system is capable of

tracking the position of markers within a 5x5 m space

within an accuracy of 1mm, at a data rate of 100 Hz.

The human to be tracked wore 41 reﬂective mark-

ers ﬁrmly attached to their body using velcro straps,

or tape (see Figure 1 and 3). In some cases there

was the possibility of loss of marker data due to self-

occlusions. This is very detrimental to the imitation

algorithm since the humanoid model depends on con-

tinous human motion data. To solve this, we imple-

mented a linear Kalman ﬁlter that estimates the posi-

tion of markers that are lost for short durations of time

(less than 0.5 seconds). If a marker is lost for periods

longer than 0.5 seconds, we assume the model to be

unrecoverable and initiate an emergency stop. The la-

tency between capture of marker data and the kalman

ﬁltered data is about 30 ms. This ﬁltered data is then

applied to the Humanoid-Normalized model.

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

Figure 3: Human→Humanoid Normalized Model→Humanoid. Motion capture position data from the human is transferred

to the normalized model and associated with the planes and humanoid joints. The motion of these planes and joints drives the

humanoid motion.

3 HUMANOID-NORMALIZED

MODEL

3.1 Why a Normalized Model?

Multon et al. (Multon et al., 2008) proposed the use

of a normalized skeleton, which acts as an intermedi-

ate entity to map motion between two different dig-

ital actors. The generation and adaptation of motion

was done by assuming that there exists planes formed

by the arms and legs. The normalized skeleton was

represented by normalized segments, limbs of vari-

able lengths and the spine. Humans come in dif-

ferent sizes and shapes, and most adults are bigger

than our humanoid HRP2. HRP2 also has two addi-

tional DoF’s in its chest (pitch and yaw) and this re-

quires special treatment unlike that for the humanoid

ASIMO, used in (Dariush et al., 2008a), where the

torso is one single joint. There is thus a need to extract

the relevant characteristics of human motion, and de-

ﬁne it in a form that is suitable for application on hu-

manoids. We extended the idea presented by Multon

and colleagues by deﬁning planes for not only the

arms, but also the head, chest and waist. The planes

are attached to the human body in such a way that they

can be directly used to deﬁne geometric tasks in the

prioritized inverse kinematics solver. A combination

of the orientation of these planes, and the position of

the extremities (head and wrists) form the Humanoid-

Normalized model (henceforth HN Model).

3.2 Components of

Humanoid-normalized Model

The physical model of the upper body was built from

the cartesian positions of 22 markers on the human

Figure 3. Before the model is computed we scale the

marker positions according to a modiﬁed version of a

standard scaling algorithm (Boulic et al., 2009). First,

we start with the head. Three markers on the head

were used to form the head virtual plane. The center

of these markers were considered in the HN model.

The normal to the plane deﬁned by these markers was

computed. In the HN model we represent the orienta-

tion of the head as the orthogonal to this normal vec-

tor. For the head, the plane normal is computed as,

head

= V

×V

(1)

where,

− p

||p

− p

||p

− p

, p

are the markers associated to the head vir-

tual plane.

Similarly, chest and waist virtual planes were con-

structed using the relevant markers such that their nor-

mals were approximately in the sagittal direction (see

Figure 3 for illustration of markers used). Virtual

planes for the arms were constructed using markers

on the shoulder, elbow and wrist. Instead of using

the positions of all these markers, the arm posture is

represented by the normal to this plane and the wrist

position. We chose this representation because of the

difﬁculty to directly map the cartesian position of all

these markers to the robot structure. In addition to up-

per body characteristics, we also included the position

of the feet in the HN model.

Thus, overall the Humanoid-Normalized model is

expressed by the following set of geometric proper-

ties:

, N

, P

, N

, P

, N

, P

l f

, P

r f

] (2)

ON REAL-TIME WHOLE-BODY HUMAN TO HUMANOID MOTION TRANSFER

where P

is a point representing the position of the

head, V

is a vector representing the orientation of the

head, N

is a vector representing the normal of the

chest plane, V

is a vector representing the orientation

of the waist, P

is a point representing the position of

the left hand, N

is a vector representing the normal

to the left arm plane, P

is a point representing the

position of the right hand, N

is a vector representing

the normal to the right arm plane, P

l f

is a point rep-

resenting the position of the left foot, P

r f

is a point

representing the position of the right foot.

4 HUMANOID INVERSE

KINEMATICS

The HN model explained in the previous section al-

lows us to retarget human motion into a form suit-

able for transfer onto the humanoid. To generate mo-

tion of the humanoid we used a task-based inverse

kinematics solver (Nakamura, 1991).

4.1 Prioritized Inverse Kinematics

Forward kinematics expresses the relationship be-

tween the variation of the joint parameters δq and

the corresponding displacement δx in the operational

space (Nakamura, 1991). This is given by,

δx = Jδq (3)

where J is the m × n jacobian matrix, m being the di-

mension of the task, and, n is the number of degrees

of freedom. The inverse kinematics model determines

the joint variation that produces an expected displace-

ment, which is obtained by solving the system in Eq.

3. However, for the humanoid robot we have m < n,

thus this linear system is under-constrained. In this

case, all the solutions of the system can be written as:

δq = J

δq + (I − J

J)z (4)

where J

= J

(JJ

)

−1

is the pseudo inverse of J, I

is the n× n identity matrix, (I −J

J) is the null-space

projector of J, and z is an n-dimensional arbitrary vec-

tor. The ﬁrst term on the right side of equation 4 is a

generic solution and z in the second term can be used

to satisfy additional constraints without modifying δx.

The generic expressions for solving n tasks with

descending order of priorities are (Siciliano and Slo-

tine, 1991):

= I

= J

i−1

= I −

δq

i+1

(δx

i+1

− J

i+1

δq

)

where N

is the projector associated with the i

task,

is the jacobian of the i

task, I is the n × n identity

matrix. The update δq

is iteratively computed for all

tasks.

4.2 Whole-body Motion Generation

The position for each joint is generated from a prior-

itized stack of tasks (Yoshida et al., 2006), which is

solved using the inverse kinematics formulation ex-

pressed above. Each property of the HN model repre-

sentation is used as the target input for the tasks. Our

task stack was deﬁned as (in decreasing priority):

1. Homogenous transformation task for each feet,

i.e. both position and orientation are ﬁxed,

2. Position task for Center of Mass (CoM) projection

(X and Y positions),

3. Position task for the head,

4. Homogenous transformation task for the left

wrist,

5. Homogenous transformation task for the right

wrist,

6. Orientation vector task for the chest,

7. Orientation vector task for the waist,

8. Orientation vector task for the head.

We use four kinds of tasks: position task, orienta-

tion vector task, homogenous transformation task and

a CoM task. As examples, we deﬁne in more detail

the task construction for the head and the arms. The

CoM task is detailed in the next section. The position

task of the head f

(θ) is deﬁned as,

(θ) = P

− P

(θ)

where P

is the target of the task given by the position

of the head in the HN model representation. P

(θ)

is the position of the humanoid head expressed as a

function of the robot dof’s θ.

For the orientation vector task of the head f

(θ)

we have

(θ) = V

×V

(θ) (5)

where V

is the target head direction, which is given

by the head orientation vector in the HN model. And

(θ) is the corresponding vector of the humanoid

head, as a function of the robot dof’s θ. The orien-

tation vector tasks for the chest and waist are deﬁned

in a similar way.

For each arm a homogeneous transformation task

is constructed for the wrist joint. The target trans-

formation is constructed from two properties, wrists

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

Figure 4: Scenario 1. (a) Snapshot of human dancing and its imitation by HRP2 (b) Roll, pitch and yaw angles of the head

joint during the dancing motion. Solid black line indicates the angles of the HN model, this was the target the humanoid had

to follow. Red circles indicate the corresponding angular value on HRP2 (c) Chest angles of the HN model (solid black line)

and the corresponding angles on the humanoid (dashed red line).

position and the normal to the HN model’s arm plane.

The target rotation matrix in the homogenous trans-

formation is computed as,

= [N

arm

×V N

arm

V ] (6)

where N

arm

is the normal of the left or right arm plane,

and V is a unit vector connecting the elbow and wrist

markers. It should be noted that the N

arm

is parallel to

the axes of the humanoid elbow joint.

5 COM ANTICIPATION MODEL

The CoM of a humanoid robot is a vital indicator to

its stability. In order to remain statically stable, the

projection of CoM on the ﬂoor should remain within

the support polygon deﬁned by the two feet of the hu-

manoid. If the human performer were to lift his/her

foot, the CoM of the humanoid robot would have to

be shifted in advance towards the other foot in order

to maintain balance. In order to know when this shift

is required, we take inspiration from results in human

neuroscience research. Studies have reported strate-

gies by which motion of the CoM in humans can be

related to foot placement and hip orientation (Patla

et al., 1999), (Vallis and McFadyen, 2005).

To manipulate the projection of the humanoid

CoM on the ﬂoor we constrain it to track a target. The

target position is computed depending on the current

stance of the HN model, i.e. Double Support (DS)

or Single Support (SS). The transition of stance from

single to double support is detected using the position

and velocity of the feet. When either of these mea-

sures exceed a pre-determined threshold a change of

stance is said to have occured. For the motion of the

CoM the target is computed as:

CoM



CoM

i−1

+ α(V

head

·V

f eet

if DS

f oot

+ βV

head

if SS

(7)

where,

CoM

= CoM X and Y positions at time step i,

head

= HN Model head 2D velocity vector,

f eet

= Unity vector across robot’s feet,

f oot

= Humanoid support foot X and Y positions,

α, β are constants.

6 IMPLEMENTATION OF

ONLINE HUMAN-HUMANOID

MOTION TRANSFER

Our framework was implemented using the software

achitecture Genom, (Fleury et al., 1997). Mainly, we

have four modules to establish communication from

the motion capture system to the HRP2 robot inter-

face. First, we have a motion capture server whose

function is to send motion data to the network via

UDP protocol. These data are ﬁltered as described

ON REAL-TIME WHOLE-BODY HUMAN TO HUMANOID MOTION TRANSFER

Figure 5: Scenario 2. (a) Picture of humanoid imitating the human lifting his foot. (b) Sideways displacement of the HN

model head (solid black line), and the vertical height of the humanoid’s lifting foot (dashed red line). Also shown is the Y

displacement of the humanoid’s CoM (dash-dot blue line). Zoom inset shows a magniﬁed view of the anticipation phase. The

anticipation occurs between the ’Balance point’ and the time when the humanoid lifts its foot.

in section 2. A second Genom module reads the

seamless motion data and computes the robot mo-

tion. This module implements the HN-normalized

model, the CoM anticipation model and the priori-

tized inverse kinematics solver. Finally, via a plugin

we send robot motion data from the motion gener-

ation Genom-module to the HRP2 interface control

panel.

We present two scenarios that illustrate the

capabilities of our algorithm. In the ﬁrst scenario

we assume the robot’s feet to be ﬁxed and imitate

the motion of a human performer executing a slow

dance with the upper body, including bending of the

knees and ankles. In the second scenario, the robot

is allowed to lift-off with one of its feet and balance

on the other foot. This was chosen to illustrate the

anticipation model which prepares the humanoid

for balancing on one foot. The parameters used for

the CoM anticipation model were, α = 0.12, β =

0.01. All computations were run on an Intel Core 2

CPU 6400 @2.13GHz, with 2GB of RAM memory.

At each solution step we required ∼30 ms to build

the Humanoid-Normalized model and to solve the

stack of tasks using a damped inverse kinematics

solver. The video of the results can be accessed at

http://homepages.laas.fr/manu/videos/motionImitation.mp4

6.1 Dancing

The human performer was asked to perform a simple

dance without stepping or sliding his feet. Figure 4-a

shows the posture of the human and the humanoid in

the middle of the dance. The motion computed by the

algorithm was smooth, without joint position or ve-

locity limit violations, and was quasi-statically stable.

Figure 4-b & c show the roll, pitch and yaw angles of

the head and chest of the HN model and those of the

humanoid robot. Despite the low priority given to the

head orientation task, we see that the yaw and pitch

angles were matched very closely, while roll angle of

the humanoid was much lesser than the HN model.

This was because the yaw and pitch axis are directly

available on HRP2 (independent of the other joints),

however, the humanoid does not have a roll axis for

the head joint. The roll variation seen in Figure 4-b

was due to the movement of the whole body. Chest

roll of the HN model was not considered, but to ac-

count for the movement of the rest of the body we

see an induced roll component on HRP2. The pitch

and yaw angles of the humanoid’s chest followed the

HN model less closely due to the lower priority of this

task. Since the arms and the head are connected to the

chest, and their respective tasks have a higher priority,

the chest joint has a reduced degree of mobility.

6.2 Foot Lift

In this scenario the human performer shifted his

weight onto one leg and maintained his balance for

a few seconds before slowly returning to rest on both

feet. Figure 5-a shows the human and the humanoid

balancing on one foot (SS stance). The motion of the

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

Table 1: Mean RMS error between HN model and hu-

manoid. Values in brackets denote the mean RMS error in

X,Y and Z positions for wrist positions, and roll (R), pitch

(P) and yaw (Y) for head, chest and waist orientations.

Property Mean RMS Mean RMS

position (m) orientation (deg)

CoM ∼ 0 -

Head ∼ 0 4.09

(R: 11.8 P: 0.22 Y: 0.26)

Left wrist 0.02 -

(X: 0.013 Y: 0.02 Z: 0.3)

Right wrist 0.05 -

(X:0.05 Y:0.017 Z: 0.08)

Chest - 4.2

(R: 1.1 P: 6.7 Y: 4.8)

Waist - 6.4

(R: 1.1 P: 4.62 Y: 0.52)

head in the HN model, and the vertical position of

the foot of the humanoid is plotted in Figure 5-b. We

observe that the head shifts towards the support foot

(right foot) before the lifting the other foot (Figure

5-b). The sideways displacement of the head reaches

the Y position of the support foot about 1s before foot

lift. Before reaching this point, the CoM projection

was derived according to Eq. 7 (DS stance). Once

the head reaches the support foot, the CoM is main-

tained at this position (referred to as “Balance Point”

in Figure 5-b). After this point, the behavior of the

CoM is dictated by a different relation (SS stance in

Eq. 7). It should be noted that for slow head motion,

the projection of the CoM and the head position co-

incide (a small offset can be seen in the zoom inset

in Figure 5-b)).

7 DISCUSSION

Among studies that have looked at human-humanoid

motion retargeting it is generally difﬁcult to deﬁne a

single metric reﬂecting the quality of motion trans-

fer. This can be because of several reasons. The

physical structure of humanoids can vary quite sig-

niﬁcantly (size, number of DoFs, range of motion

etc). Moreover, deﬁning a mathematical term to the

rather abstract idea of “good” motion imitation is not

clear. Dariush and colleagues, formulated a measure

for “tracking error” to express the effectiveness of

their algorithm. We employ a similar strategy and ad-

ditionally investigate the limitations of our approach

vis-

a-vis dynamic stability of the humanoid.

7.1 Quality of Motion Imitation

Quality of motion imitation was quantiﬁed by mea-

suring the root mean square error between the target

(HN model) and the humanoid robot. Table 1 lists

the relevant parameters and the errors. The position

of the CoM and head were tracked almost prefectly.

This was because both these tasks had a very high

priority. Comparitively, head orientation which had

a lower priority had a mean error of 4 deg. But it

should be noted that most of this error was because of

the roll angle (HRP2 does not have a head roll axis).

The right wrist position error was slightly larger that

the left wrist. This can be attributed to the fact that

left wrist task came before the right wrist task in the

priority list. Thus, once the left wrist position and

orientation was ﬁxed, it became more difﬁcult for the

right wrist to reach exactly its target transformation.

Comparing across studies, Dariush et al. 2008b, re-

ported an error of about 0.02 m in tracking the wrist

position while assigning them to a “medium priority

group”. In our case the head was the highest prior-

ity, and hence a low error, while the hands were low

priority, hence the larger error. Chest and waist orien-

tation were lower in the priority list and hence show

larger errors in orientation than the other joints. Over-

all, these results show that we were able to retarget a

large part of the motion of the human onto the hu-

manoid.

7.2 Limitations

We analysed the limitations of our imitation sys-

tem, and those of our humanoid, by setting up the

following test. We attached the marker set on the

performer and he was asked to move his right hand

in an up-and-down motion at different speeds. After

transferring the motion to the humanoid, we observed

the shift of the Zero Moment Point (ZMP) of the hu-

manoid for the different human hand speeds. For the

up and down motion, we detect the maximum and

minimum values of the ZMP components, and check

if it is inside the supporting polygon. We found that

the humanoid became unstable when the hand speed

was higher than 1 m/s (Figure 6). This example illus-

trates the limitations of using inverse kinematics with-

out considering, simultaneously, the dynamic stability

of the humanoid. To truly imitate both the kinematics

and dynamics of the human motion, it would be im-

portant to take both of these into account during the

modeling stage itself. For example, using a dynami-

cal model (exact or simpliﬁed) at the motion planning

stage could be a useful in this regard.

Kanehiro et al. (Kanehiro et al., 2008b), devised a

ON REAL-TIME WHOLE-BODY HUMAN TO HUMANOID MOTION TRANSFER

Figure 6: (a) Illustration of the hand up and down motion on

the simulated HRP2, (b)Plot of ZMP of the humanoid robot

vs. human hand velocities. Illustrated is the point at which

the humanoid becomes unstable because of excessive hand

speeds.

way to optimize quasi-static humanoid motion, such

that it can be performed faster, but also within the dy-

namic limits of the humanoid. We recorded the online

dancing motion of the humanoid, and optimized it of-

ﬂine to see how much faster the same motion could

be played. We found that our original 60 seconds

of dancing motion could be optimized to 31 seconds

while respecting the kinematic and dynamic limits of

the humanoid HRP2. Thus, ofﬂine optimization could

serve as a benchmark in judging how effective and ro-

bust online motion retargeting algorithms really are.

Finally, one limitation of our formulation of the

HN model is that it cannot guarantee self-collison

avoidance on the humanoid. This could be included at

the inverse kinematics stage by deﬁning self-collison

avoidance as a constraint (Dariush et al., 2008a) (Ka-

noun, 2009) (Kanehiro et al., 2008a).

8 SUMMARY AND FUTURE

PERSPECTIVES

In this study we have presented an online method

by which a humanoid robot can imitate human mo-

tion. The evaluation of the results show that the mo-

tion generated by the humanoid closely resembles the

original human motion. The proposed CoM antici-

pation model allows the humanoid to balance itself

on one foot taking the cue from the human. This

model inspired from neuroscience research opens up

new windows towards incorporating biological prin-

ciples in humanoid motion control (Berthoz, 2000),

(Sreenivasa et al., 2009). The use of the Humanoid-

Normalized model allows standardization across an-

thropomorphic ﬁgures irrespective of proportions (for

example marionettes). To further improve imitation it

could be interesting to consider the exact dynamics of

the humanoid, as well as self-collison avoidance, in

the motion planning algorithm. At the present state of

this work, we can say that our humanoid robot HRP-

2, is capable of mimicking Tai-chi like movements,

but not yet quite at the level of Karate.

ACKNOWLEDGEMENTS

F.J. Montecillo-Puente beneﬁts of a Mexican

CONACyT, SEP grant. The authors would like to

thank Anthony Mallet, Tan Viet Anh Truong and

Oussama Kanoun for taking part in helpful discus-

sions and assisting with the experiments on HRP2

and motion capture. Part of this work is supported by

the French ANR Project Locanthrope.

REFERENCES

Berthoz, A. (2000). The brain’s sense of movement. Har-

vard University Press, Cambridge, MA.

Boulic, R., Maupu, D., and Thalmann, D. (2009). On scal-

ing strategies for the full body interaction with vir-

tual mannequins. Journal Interacting with Computers,

Special Issue on Enactive Interfaces, 21(1-2):11–25.

Chois, K. J. and Ko, H. S. (December 2000). Online motion

retargetting. The Journal of Visualization and Com-

puter Animation, 11(5):223–235.

Dariush, B., Gienger, M., Arumbakkam, A., Goerick, C.,

Zhu, Y., and Fujimura, K. (2008a). Online and mark-

erless motion retargeting with kinematic constraints.

In IEEE/RSJ International Conference on Intelligent

Robots and Systems, pages 191–198.

Dariush, B., Gienger, M., Jian, B., Goerick, C., and Fu-

jimura, K. (2008b). Whole body humanoid control

from human motion descriptors. In IEEE Interna-

tional Conference on Robotics and Automation, pages

2677–2684.

Fleury, S., Herrb, M., and Chatila, R. (1997). Genom: A

tool for the speciﬁcation and the implementation of

operating modules in a distributed robot architecture.

In IEEE/RSJ International Conference on Intelligent

Robots and Systems, pages 842–848.

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

Kanehiro, F., Lamiraux, F., Kanoun, O., Yoshida, E., and

Laumond, J.-P. (2008a). A local collision avoidance

method for non-strictly convex polyhedra. Robotics:

Science and Systems, IV.

Kanehiro, F., Suleiman, W., Lamiraux, F., Yoshida, E., and

Laumond, J.-P. (2008b). Integrating dynamics into

motion planning for humanoid robots. In IEEE/RSJ

International Conference on Intelligent Robots and

Systems, pages 660–667.

Kanoun, O. (2009). Task-driven motion control for hu-

manoid robots. PhD thesis, LAAS-CNRS; Universit

de Toulouse.

Multon, F., Kulpa, R., and Bideau, B. (2008). Mkm: A

global framework for animating humans in virtual re-

ality applications. Presence: Teleoper. Virtual Envi-

ron., 17(1):17–28.

Nakamura, Y. (1991). Advanced Robotics: Redundancy and

Optimization. Addison-Wesley Longman Publishing,

Boston.

Nakaoka, S., Nakazawa, A., Kanehiro, F., Kaneko, K.,

Morisawa, M., and Ikeuchi, K. (2005a). Task model

of lower body motion for a biped humanoid robot

to imitate human dances. In IEEE/RSJ International

Conference on Intelligent Robots and Systems, pages

3157–3162.

Nakaoka, S., Nakazawa, A., Kanehiro, F., Kaneko, K.,

Morisawa, M., and Ikeuchi, K. (2005b). Task model

of lower body motion for a biped humanoid robot

to imitate human dances. In IEEE/RSJ International

Conference on Intelligent Robots and Systems, pages

3157–3162.

Patla, A., Adkin, A., and Ballard, T. (1999). Online steer-

ing: coordination and control of body center of mass,

head and body reorientation. Experimental Brain Re-

search, 129(4):629–634.

Ruchanurucks, M., Nakaoka, S., Kudoh, S., and Ikeuchi,

K. (2006). Humanoid robot motion generation with

sequential physical constraints. In IEEE Interna-

tional Conference on Robotics and Automation,, pages

2649–2654.

Schaal, S., Ijspeert, A., and Billard, A. (2003). Com-

putational Approaches to Motor Learning by Imita-

tion. philosophical transactions: biological sciences,

358(1431):537–547. philosophical transactions: bio-

logical sciences (The Royal Society).

Shon, A., Grochow, K., and Rao, R. (2005). Robotic imita-

tion from human motion capture using gaussian pro-

cesses. In 5th IEEE-RAS International Conference on

Humanoid Robots.

Siciliano, B. and Slotine, J. (1991). A general frame-

work for managing multiple tasks in highly redundant

robotic systems. In IEEE Internatioal Conference on

Advanced Robotics, pages 1211–1216.

Sreenivasa, M.-N., Soueres, P., Laumond, J.-P., and

Berthoz, A. (2009). Steering a humanoid robot by its

head. In IEEE/RSJ International Conference on Intel-

ligent Robots and Systems.

Suleiman, W., Yoshida, E., Kanehiro, E., Laumond, J.-P.,

and Monin, A. (2008). On human motion imitation by

humanoid robot. In IEEE International Conference on

Robotics and Automation.

Takano, W., Yamane, K., and Nakamura, Y. (2007). Cap-

ture database through symbolization, recognition and

generation of motion patterns. In IEEE International

Conference on Robotics and Automation, pages 3092–

3097.

Ude, A., Atkeson, C., and M., R. (2004). Programming

full-body movements for humanoid robots by obser-

vation. In Robotics and Autonomous Systems, vol-

ume 47, pages 93–108.

Vallis, L. and McFadyen, B. (2005). Children use different

anticipatory control strategies than adults to circum-

vent an obstacle in the travel path. Experimental Brain

Research, 167(1):119–127.

Vukobratovic, M. and Stepanenko, J. (1972). On the stabil-

ity of anthropomorphic systems. Mathematical Bio-

sciences, 15:1–37.

Yamane, K. and Hodgins, J. (2009). Simultaneous tracking

and balancing of humanoid robots for imitating hu-

man motion capture data. In IEEE/RSJ International

Conference on Intelligent Robots and Systems, pages

2510–2517.

Yoshida, E., Kanoun, O., Esteves, C., and Laumond, J.-

P. (2006). Task-driven support polygon humanoids.

In IEEE-RAS International Conference on Humanoid

Robots.

ON REAL-TIME WHOLE-BODY HUMAN TO HUMANOID MOTION TRANSFER