
OFFROAD NAVIGATION USING ADAPTABLE MOTION PATTERNS
Frank Hoeller, Timo R
¨
ohling and Dirk Schulz
Fraunhofer Institute for Communication, Information Processing and Ergonomics FKIE, Germany
Keywords:
Outdoor robotics, Local navigation, Motion patterns, Motion templates, Motion learning.
Abstract:
This paper presents a navigation system which is able to steer an electronically controlled ground vehicle to
given destinations considering all obstacles in its vicinity. The approach is designed for vehicles without a
velocity controlled drivetrain and without an odometry system, making it especially useful for typical remote-
controlled vehicles without upgrading the motor controllers. The vehicle is controlled by sets of commands,
each set representing a specific maneuver. These sets are then combined in a tree-building procedure to form
trajectories towards the given destination. While the sets of commands are executed the vehicle’s movement
is measured to refine the prediction used for path generation. This enables the approach to adapt to surface
alterations. The technique requires a precise position estimation, which is provided in our implementation by
a 3D laser mapping based relative localization system. We tested our approach using a 400kg EOD robot in
an outdoor environment. The experiments confirmed that our navigation system is able to control the robot to
its destination while avoiding obstacles and adapting to different ground surfaces.
1 INTRODUCTION
In the design of robot systems operating in unstruc-
tured outdoor environments, special care has to be
taken that the robots do not accidentally collide with
obstacles in their vicinity. Compared to indoor situ-
ations the robot can suffer drastically more damage
by the more hazardous surrounding. Safe operation
is commonly achieved by means of collision avoid-
ance mechanisms which ensure a minimal distance
to obstacles. This task is exacerbated by different
ground surfaces which have a distinct effect on the
wheel grip. This deviation has to be anticipated to en-
sure the reproducibility of planned motions and thus
making collision avoidance possible.
Additional complications arise for robots which
were designed for remote-control. Such robots are
normally only equipped with relatively simple mo-
tor controllers. This has a significant impact on the
techniques available for the collision avoidance be-
cause most classic navigation algorithms only gener-
ate velocity commands. To interpret such commands
the controllers need to have an appropriate servo loop,
which is not the case for such robots.
In this article we present an approach which al-
lows a mobile robot with any kind of electronic mo-
tor controller to operate in cluttered outdoor environ-
ments. To be able to improve the navigation behavior
Figure 1: The Quinetiq Longcross robot Suworow equipped
with a Velodyne 3D and an additional (unused) 2D laser
range finder.
of the robot in unknown locations, our approach fol-
lows a local navigation paradigm and does not need a
map of the environment. Instead, the robot’s motion
control decides solely based on the robot’s sensory in-
put; in our current implementation this is a Velodyne
3D laser range scanner with 360 degree field of view
which is used to compute a local 2.5D map. In ad-
dition, the laser scanner is used to exactly determine
the robot position in a local frame of reference using
a local mapping technique. This procedure also com-
pensates the missing robot odometry.
The motion planning for the robot is based on a
tree-search technique which we developed to suit the
special requirements of the robot’s motor controllers.
Our planning algorithm composes paths by combin-
186
Hoeller F., Röhling T. and Schulz D. (2010).
OFFROAD NAVIGATION USING ADAPTABLE MOTION PATTERNS.
In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 186-191
DOI: 10.5220/0002916301860191
Copyright
c
SciTePress

ing predefined Motion Patterns. Each Motion Pat-
tern consists of a set of robot commands and a se-
ries of poses which represent the robot’s movement
when the command set is executed by the controllers.
With these Motion Patterns, the local navigation mod-
ule repeatedly computes trees of collision-free com-
mand sequences. From each tree a path is extracted
which brings the robot close to the destination coordi-
nate as fast as possible. To tackle the surface traction
problem, the robot’s movements are measured on the
fly. The collected data is used to update the measured
movement part of the Motion Patterns. The upgraded
Motion Patterns are handed over to the planning pro-
cess and used for the tree generation.
The remainder of this article is organized as fol-
lows: After discussing related work in section 2, we
introduce our Velocity Grid environment representa-
tion in section 3 followed by a description how they
are utilized by our Motion Pattern based local navi-
gation approach in Section 4. Section 5 then explains
the movement measuring and Motion Pattern learning
procedures. Before we conclude, we describe some
experiments carried out with our robot to illustrate the
capabilities and the robustness of our approach. We
implemented our approach on a Quinetiq Longcross
EOD robot (see Figure 1) and verified its feasibility
in outdoor settings.
2 RELATED WORK
Waypoint navigation is one of the fundamental tasks
for autonomous mobile robots. Many popular sys-
tems utilize the benefits of cars with ackermann steer-
ings by first generating a feasable path and then try to
follow this path as fast as possible. This can be done
because, apart from physical limitations of the vehi-
cle, the velocity does not affect the trajectory. For ex-
ample, the DARPA Grand Challenge winning robot
Stanley (Thrun et al., 2006) benefits from this prin-
ciple. But because our robot does not have a veloc-
ity controlled drivetrain, the velocity cannot be con-
trolled without affecting the trajectories.
Another approach (V. Hundelshausen et al., 2008)
uses a different navigation technique by defining
a limited set of commands or command-sequences
and greedily decides in every computing interval
which entity should be applied. Their path genera-
tor uses combinations of speeds and steering angles
to generate trajectories which are then further eval-
uated. Therefor, an occupancy grid generated by a
3D-laser and different weighting functions are used.
This is similar to the Dynamic Window Approach
(DWA) (Fox et al., 1997; Brock and Khatib., 1999)
because both methods restrict the search to a single
time step, i.e. they select the next best controls based
on the current sensor input and a model of the robot’s
dynamics.
In addition to these pure navigation algorithms,
learning methods for robot motion have also been pro-
posed in the past. Future robot positions can be es-
timated by regarding the current terrain type (Brun-
ner et al., 2010). Therefor, intertial sensor data is
processed with Gaussian process models to infer the
movement velocities for position estimation and to
deduce the terrain type from vibrations. Unfortu-
nately, this method can only distinguish known sur-
faces and the used models require large amounts of
computational power. Gaussian Processes in com-
bination with reinforcement learning have been used
to predict the movement of autonomous blimps (Ko
et al., 2002), but just as the approach above it requires
an extensive preparation phase. Seyr et al. use arti-
ficical neural networks to predict the trajectories of a
two-wheeled robot (Seyr et al., 2005). It was shown
that every trained situation can be recognized by their
predictor. The used robot model is heavily bound to
velocity parameters and thus again requires a suitable
drivetrain.
The concept of motion template based learning
has been previously employed to simplify the learn-
ing of complex motions (Neumann et al., 2009). In
contrast to our approach the templates have param-
eters which are adjusted to fit the desired trajectory.
This implies a feasible correlation between parameter
input and drivetrain behavior.
3 VELOCITY GRIDS
In outdoor environments, a 3D-sensor (see Figure 1)
is indispensable for an effective collision avoidance.
Commonly used two-dimensional indoor variants are
almost useless because of their insufficient envi-
ronment coverage. However, the gain in coverage
comes with the disadvantage of a drastically increased
amount of data. Processing all this information while
planning motions requires an unreasonable amount of
computing power. Thus we simplify the 3D-sensor’s
data to a two-dimensional grid. In every grid cell the
maximum admissible velocity of the corresponding
area is stored. This type of map is referred to as Ve-
locity Grid and it can be used for collision tests with
less operating expense. This allows us to use modi-
fied two-dimensional planning algorithms. Although
Velocity Grids seem to be similar to costmaps, they
are utilized by our local navigation algorithm in a dif-
ferent way (see section 4).
OFFROAD NAVIGATION USING ADAPTABLE MOTION PATTERNS
187

Figure 2: Left: A 2.5D height map acquired using a Velo-
dyne. Right: The corresponding Velocity Grid. A car and
the following person are marked as impassable (red), the
sidewalk’s curb is identified as slowly traversable (yellow).
To generate a Velocity Grid, the first step is to cal-
culate a 2.5D map or height grid. A simple method
to do this is to use a maximum-function on all mea-
surements corresponding to one cell. Of course more
sophisticated approaches could be used here, even
including terrain classification (Vallespi and Stentz,
2008; Wellington et al., 2005), but all of these ap-
proaches require additional computation power and
introduce additional delay. Since low latency and suf-
ficient computing power are requirements for the fol-
lowing navigation approach, the simple mechanism
was chosen over more intelligent algorithms. An ex-
ample height grid is shown on the left in Figure 2. The
information on the floor height now has to be trans-
formed to a format which can easily be used for col-
lision checks. For this purpose, we follow a line from
the robot’s center to every border cell of the Velocity
Grid. Along this line the elevation changes are calcu-
lated, an appropriate maximum speed dependent on
the robot’s capabilities is chosen and assigned to the
second of the two involved cells. This corresponds
to extracting level curves in a star-like shape with the
star’s center in the center of the robot and categorizing
the stepping of each curve into speed groups. Because
of the Velocity Grid’s geometry it is guaranteed that
every cell is at least processed once. On the right of
Figure 2 the outcome of this algorithm can be seen.
During the Velocity Grid calculation, it is assumed
that the robot always moves in straight lines away
from the center. For a robot that can turn on the spot
this is a good estimate for the direct proximity, but
a single Velocity Grid cannot be used for the plan-
ning and execution of a u-turn or similar. It has to
be considered, that the Velocity Grid is continuously
updated, several times per second, to ensure that new
obstacle information reaches the motion planning in
time. As soon as the planning module realizes that its
previous path is invalid, it will generate a new trajec-
tory with respect to the freshly detected obstacles.
4 USING MOTION PATTERNS
FOR LOCAL NAVIGATION
4.1 Motion Patterns
The core of the overall approach is a local naviga-
tion planning component which directly controls the
robot and steers it from its current position to a given
destination on a collision-free path in configuration
space. In our case a configuration c
t
= (x, y, θ, v)
>
t
of
the robot at time t consists of the robot’s position and
heading (x
t
, y
t
, θ
t
)
>
as well as its translational veloc-
ity v
t
. In order to simplify the planning process, the
rotational velocity is not considered here. Destination
coordinates d of the local navigation are also defined
as four dimensional vectors d = (x, y, θ, e)
>
, but in-
stead of a velocity they contain a distance threshold
e which defines a circle around the target coordinate.
When the robot reaches this circle, the destination is
considered reached, a technique which has also been
used by Bruch et al. (Bruch et al., 2002). Since the
robot is controlled by motor power commands instead
of velocity commands, the outcome of a command
depends on many factors and is far too expensive to
compute.
Thus we introduce Motion Patterns to simplify the
motion planning. The first component of each Mo-
tion Pattern is a series of robot control commands.
These commands can be of any type; when used with
a Longcross robot, they are motor power commands.
This set of commands is static and not changed. The
second component of a Motion Pattern is an array
of oriented positions. It represents the trajectory on
which the robot would probably move when the com-
mand series is sent to the robot. Together with the di-
mensions of the robot, the path the robot would take
can be calculated and checked for collisions using the
Velocity Grid described in section 3. This is a popu-
lar technique, because it “allows computing the cost
of a motion without explicitly considering the mo-
tion itself” (Pivtoraiko et al., 2009). Notice that the
number, shape, and complexity of Motion Patterns
are not restricted, but definitely have an impact on the
later described planning process. To combine Motion
Patterns to a continuous path we have to make sure
that the transitions between the chosen patterns are
smooth. To accomplish this, the initial and final ve-
locities are stored with every pattern. Furthermore,
every Motion Pattern is assigned to a velocity group
depending on its maximum speed. This property is
used as criterion for exclusion.
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
188

4.2 Path Planning
Based on the model above, we can now build a
collision-free tree of Motion Patterns T = (V, E) con-
sisting of nodes V and possible transitions E between
nodes. Every node V represents a Motion Pattern.
The root node is defined by the final state of the cur-
rently applied Motion Pattern. New nodes are created
in a breadth-first manner and are connected to their
parent node if they meet the following three require-
ments:
1. The node’s initial velocity matches the final ve-
locity of its parent.
2. It is possible to apply the assigned Motion Pattern
at the final position of the parent. In detail: the
minimum speed of the cells, which the node tra-
verses in the Velocity Grid, does not exceed the
Motion Patterns maximum speed. This implies
the absence of collisions.
3. The occurring roll and pitch angles are within the
robot’s safe operational parameters.
After adding a node, a weight-equivalent is assigned:
Since the planning algorithm intends to find the
fastest path to a given destination, distances between
two configurations c
i
and c
j
are represented by the
approximated travel time h(c
i
, c
j
). This way it is pos-
sible to subsume the robot’s current orientation, the
spatial distance to, and the orientation of the destina-
tion into one scalar.
h(c
i
, c
j
) =
d(c
i
, c
j
)
v
avg
+ s
(|α(c
i
, c
j
)| + |β(c
i
, c
j
)|)
ω
avg
(1)
Here d(c
i
, c
j
) represents the line-of-sight distance to
the target, v
avg
denotes the robot’s average transla-
tional speed, and ω
avg
is the average rotational veloc-
ity. The angle α(c
i
, c
j
) describes the difference be-
tween the robot’s heading in state c
i
and the line-of-
sight between c
i
and c
j
. Similarly, β(c
i
, c
j
) is defined
as the difference between the heading of the target c
j
and the line-of-sight. The idea behind this heuristic is
to separate the motion from c
i
to c
j
into a rotation on
the spot, followed by a straight line motion, followed
again by a final rotation on the spot. Of course the
robot generally translates and rotates simultaneously.
The numerical constant s is introduced to account for
the resulting speed advantage. If the destination’s
heading θ is undefined, β is set to zero. During the
tree creation the node with the smallest h is marked.
To ensure an effective movement, nodes which reach
the destination threshold area should always be supe-
rior to other nodes, regardless of their h-value. Cer-
tainly the heuristic function does not guarantee that
the destination pose is precisely reached but it always
Figure 3: A tree of collision free paths that has been build
using Motion Patterns in an 2-dimensional simulated envi-
ronment. This tree would be used for planning.
delivers a feasible path which at least moves the robot
closer to the target area. Furthermore, the constant s
defines how hard our approach tries to match the des-
tination’s orientation.
The Velocity Grids are not used to sum up the
costs of a potential path. Instead they are used as ex-
clusion criterion for potentional Motion Patterns. The
chosen Motion Patterns then define the cost.
The creation of new nodes is aborted when a suf-
ficient tree depth or a time limit is reached. A poten-
tial new path is available after a tree is constructed.
To be certain that a new path is available in time, the
tree construction has to be finished before the Motion
Pattern which is currently applied by the robot, is ex-
ecuted completely. To ensure this, the time limit for
the tree construction process is equivalent to the time
consumption of the quickest Motion Pattern available.
As mentioned before, the size of the Motion Pat-
tern pool has a significant impact on the generated
tree: While more available patterns enhance the qual-
ity of the resulting tree, they also decrease the tree
depth that can be reached in the computation time
window. A suitable quantity of Motion Patterns has to
be choosen with respect to the capabilities of the used
computer. An example tree from our current imple-
mentation can be seen in Figure 3. The used Motion
Pattern pool consisted of five different basic maneu-
vers: accelerate, decelerate, turn left, turn right and
move forward.
Using the previously marked node, a series of Mo-
tion Patterns representing a path towards the destina-
tion can be extracted from the tree.
5 MOTION LEARNING
A problem arising from our special kind of local navi-
gation is its sensitivity to surface and traction changes.
Motion Patterns are created for specific surfaces only.
And it is unlikely that the surface or the surface’s con-
dition always remains constant, especially in outdoor
OFFROAD NAVIGATION USING ADAPTABLE MOTION PATTERNS
189

movement information
Laser scanner
range data
Terrain evaluation
Planer
Velocity Grid
Motor controllers
chosen
Motion Pattern
Learning module
updated Motion Patterns
IMU
chosen Motion Pattern
Figure 4: A flowchart showing the navigation process and
the intregation of the learning mechanism.
scenarios. To compensate this, a basic learning mech-
anism has been added: While the command set of a
Motion Pattern is executed, the robot’s reactions are
measured with the on-board IMU. Recorded are the
relative x and y positions and the orientation. The
measurements are integrated in the Motions Pattern’s
existing prediction using a component-by-component
exponential smoothing function to allow continuous
learning:
¯m
p,t
= (1− w)m
p,t
+ (w) ¯m
p,t−1
(2)
with 0 ≤ w < 1. Here m
p,t
is the measured trajec-
tory of a Motion Pattern p at time t. ¯m
p,t−1
represents
the existing prediction of the pattern and ¯m
p,t
the up-
dated prediction. To limit the impact of new measure-
ments, w should not be larger than
1
2
. Note that it is
not possible to adapt the command sequence to match
the desired trajectory, because the mapping from tra-
jectories to commands is unknown and possibly not
even computable. Figure 4 depicts how the learning
mechanism is integrated in the navigation process.
A side effect of the Motion Pattern adaption is the
possibility of pattern pool depletion: It occurs when
an update causes one or more patterns to become best
suited for a specific maneuver that was previously
covered by another pattern. As the original Motion
Pattern will not be used any more, it cannot be up-
dated and remains unused. In order to counteract this
effect, we delay pattern updates until new motion data
for all Motion Patterns has been collected. Then, we
update all patterns at once. The drawback of this
method is that the trajectory construction will be less
accurate due to outdated Motion Patterns.
Between the pattern updates some Motion Pat-
terns will be executed more frequently than others.
Therefore, we apply a secondary exponential smooth-
ing with a much larger w which tracks the amount
of change that is to be applied with the next update.
This technique effectively balances the disproportion-
ate impact that more frequently used Motion Patterns
have on the pattern pool.
Figure 5: The obstacle course and the path autonomously
driven by the robot.
6 EXPERIMENTAL RESULTS
6.1 Obstacle Course
To show the functionality of our navigation planning
system, we set up an obstacle course with a length
of about 50 m. Figure 5 shows the trajectory driven
by the robot. The 50 m course was completed in 60
seconds. With an average Motion Pattern speed of
1.25 m/s this might sound surprising, but the robot ex-
ecuted a backward motion at the beginning and a turn-
on-the-spot maneuver at the end of the course, which
slowed it down. Notice that our system does not use
global maps and thus was never meant to find opti-
mal routes. To prevent such correction maneuvers, an
additional global navigation is required.
6.2 Changing Surface
The second experiment demonstrates the adaption ca-
pabilities on a surface with varying characteristics.
Therefor, a series of GPS-waypoints resulting in a to-
tal path lenght of approximately 260 m was given to
the local navigation. The experiment was conducted
with and without the learning mechanism. The aver-
age Motion Pattern speed was 1.25m/s again.
To compare the performance, the absolute devia-
tion from the predicted trajectory was measured for
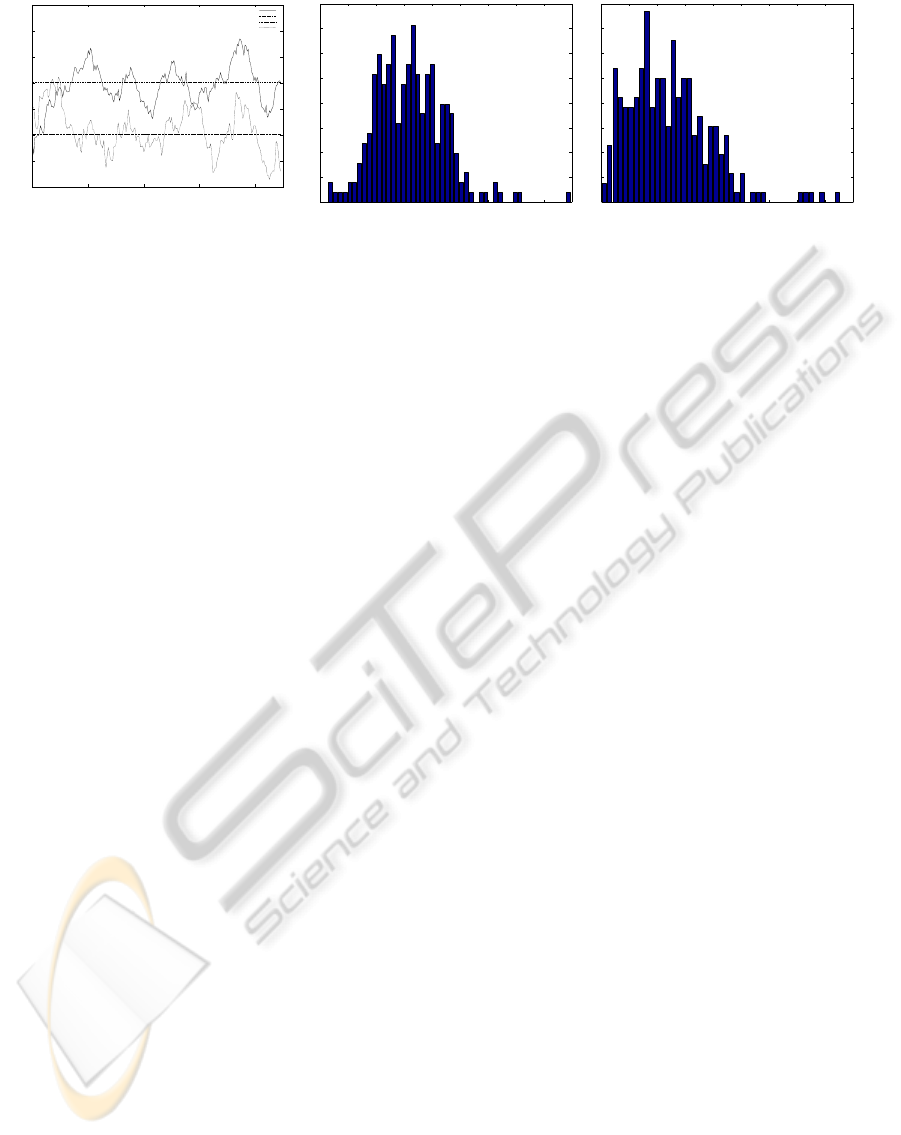
every executed Motion Pattern. The results are vi-
sualised using a rolling average on the left of Fig-
ure 6. The mean error without learning was 0.16 m
and decreased by 18% (t-test significance >95.5%)
with learning. Also, the total legth of the driven path
was somewhat shorter. This seems to indicate a posi-
tive effect of the learning mechanism on the path plan-
ning. The two histrograms in Figure 6 show the er-
ror distributions for each setup. Both distributions are
roughly normal and corroborate our findings.
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
190
0.08
0.1
0.12
0.14
0.16
0.18
0.2
0.22
0 50 100 150 200
error per meter (m)
time (s)
rolling average w/o learning
average w/o learning
rolling average with learning
average with learning
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45
0
1
2
3
4
5
6
7
8
%
error per meter (m)
0 0.05 0.1 0.15 0.2 0.25 0.3 0.35 0.4 0.45
0
1
2
3
4
5
6
7
8
%
error per meter (m)
Figure 6: Experimental results: Left: The rolling and total average of the two setups. The learning variant outperforms the
static version. Middle and right: Histogram showing the absolute error distribution without and with learning. Right: Large
errors occur less frequent.
7 SUMMARY AND
CONCLUSIONS
In this paper we presented a navigation system based
on predefined motion templates which are combined
with a tree-search technique to achieve efficient tra-
jectories. We introduced Velocity Grids to represent
difficult or impassable terrain by means of a maxi-
mum admissible velocity. The system has the ability
to adjust the motion templates according to the actual
robot movement, which is measured by an IMU, GPS,
and lidar-based motion estimation. The soundness of
our approach has been shown both in real-word navi-
gation tasks. The system proved that it can navigate a
robot through an obstacle course, and that it is able to
adapt to different surfaces quickly.
Future work will focus on improving the perfor-
mance of the motion learning and adapting mecha-
nisms. The current countermeasure against pattern
pool depletion causes temporarily outdated predic-
tions. The most promising remedy would be to prop-
agate the changes of one Motion Pattern to all others,
provided that a sufficiently precise online approxima-
tion can be found. Another improvement worth inves-
tigating is the usage of the pattern deviation that is de-
termined by the learning module as uncertainty mea-
sure in order to optimize the Motion Patterns’ safety
margins.
REFERENCES
Brock, O. and Khatib., O. (1999). High-speed navi-
gation using the global dynamic window approach.
In Proc. of the IEEE International Conference on
Robotics & Automation (ICRA).
Bruch, M., Gilbreath, G., and Muelhauser, J. (2002). Ac-
curate waypoint navigation using non-differential gps.
In Proc. of AUVSI Unmanned Systems.
Brunner, M., Schulz, D., and Cremers, A. B. (2010). Po-
sition estimation of mobile robots considering char-
acteristic terrain model. In submitted to the Interna-
tional Conference on Informatics in Control, Automa-
tion and Robotics (ICINCO).
Fox, D., Burgard, W., and Thrun, S. (1997). The dy-
namic window approach to collision avoidance. IEEE
Robotics & Automation Magazine, 4(1):23–33.
Ko, J., Klein, D., Fox, D., and Haehnel, D. (2002). Vision-
based Monte-Carlo self-localization for a mobile ser-
vice robot acting as shopping assistant in a home store.
In Proc. of the IEEE/RSJ International Conference on
Intelligent Robots and Systems (IROS).
Neumann, G., Maass, W., and Peters, J. (2009). Learning
complex motions by sequencing simpler motion tem-
plates. In Proc. of the International Conference on
Machine Learning (ICML).
Pivtoraiko, M., Knepper, R. A., and Kelly, A. (2009). Dif-
ferentially constrained mobile robot motion planning
in state lattices. J. Field Robot., 26(3):308–333.
Seyr, M., Jakubek, S., Novak, G., and Dellaert, F. (2005).
Neural network predictive trajectory tracking of an
autonomous two-wheeled mobile robot. In Interna-
tional Federation of Automatic Control (IFAC) World
Congress.
Thrun, S., Montemerlo, M., Dahlkamp, H., Stavens, D.,
Aron, A., Diebel, J., Fong, P., Gale, J., Halpenny,
M., Hoffmann, G., Lau, K., Oakley, C., Palatucci, M.,
Pratt, V., Stang, P., and Strohband, S. (2006). Winning
the darpa grand challenge. Journal of Field Robotics.
V. Hundelshausen, F., Himmelsbach, M., Hecker, F.,
Mueller, A., and Wuensche, H.-J. (2008). Driving
with tentacles: Integral structures for sensing and mo-
tion. J. Field Robot., 25(9):640–673.
Vallespi, C. and Stentz, A. (2008). Prior data and ker-
nel conditional random fields for obstacle detection.
In Proceedings of the Robotics: Science and Systems
(RSS).
Wellington, C., Courville, A., and Stentz, A. (2005). Inter-
acting markov random fields for simultaneous terrain
modeling and obstacle detection. In Proceedings of
the Robotics: Science and Systems (RSS).
OFFROAD NAVIGATION USING ADAPTABLE MOTION PATTERNS
191
