MATCHING PURSUITS BASED ON PERCEPTUAL DISTORTION

MINIMIZATION FOR SINUSOIDAL AUDIO MODELLING

N. Ruiz Reyes, P. Vera Candeas, F. J. Ca˜nadas, J. J. Carabias, P. Caba˜nas and F. Rodriguez

Telecommunication Engineering Department, University of Ja´en, Polytechnic School, Linares, Ja´en, Spain

Keywords:

Sinusoidal modeling, Matching pursuit, Perceptual distortion, Audio coding, Overcomplete dictionary, Sparse

approximation, Complex exponentials.

Abstract:

In this paper, we propose an improved sinusoidal audio modeling method for perceptual matching pursuits

driven by a perceptual distortion measure. A linear model derived from the effective signal processing in the

ear is used for computing the perceptual distortion measure. This distortion measure allows us to select the

most perceptually meaningful sinusoid at each iteration of the pursuit. Furthermore, the distortion measure

can be used to deﬁne a psychoacoustic stopping criterion for the matching pursuit algorithm. The proposed

sinusoidal modeling method is designed to be used in sinusoidal audio coding. Our method provides signiﬁcant

advantages regarding previous works because it achieves a better separation between tones and noise, as can

be seen in results.

1 INTRODUCTION

Sinusoidal audio coding is a promising technique for

audio signal characterization, compression and mod-

iﬁcation (MPEG, 2003)(Goodwin, 1998). Sinusoidal

modelling is able to parameterize most of the audio

signal energy in a small set of parameters because au-

dio signals are often strongly tonal.

The classical sinusoidal model (McAulay and

Quatieri, 1986) comprises an analysis-synthesis

framework that represents a signal x[n] as the sum of

a set of K sinusoids with time-varying frequencies,

phases, and amplitudes:

x[n] ≈ ˆx[n] =

∑

k=1

[n] · cos

[n] · n+ φ

[n]

(1)

where A

[n], ω

[n] and φ

[n] represent the time-

varying amplitude, frequency and phase of the k-th

sinusoid.

Since an audio signal is typically non-stationary,

it must be properly segmented in such a way that

the sinusoidal parameters (amplitude, frequency and

phase) change very little along each analysis audio

frame. Assuming that parameters of expression (1)

do not change considerably along the analysis frame,

they can be made constant within a frame (A

, ω

, φ

)

and the signal can be reconstructed from these sinu-

soidal parameters on a frame-by-frame basis.

A large number of methods has been proposed

in the literature for estimating the parameters of the

sinusoidal model. This is typically accomplished

by peak picking the Short-Time Fourier Transform

(STFT). Usually, analysis-by-synthesis is used in or-

der to verify the detection of every spectral peak. In

this paper we focus on the matching pursuit algorithm

(Mallat and Zhang, 1993), that is a particular analysis-

by-synthesis method.

Matching pursuit is an iterative algorithm that of-

fers a sub-optimal solution for decomposing a signal

x in terms of unit-norm expansion functions g

cho-

sen from an overcomplete dictionary D. At the ﬁrst

iteration, the function (or atom) g

which gives the

largest inner product with the analyzed signal x is

chosen. The contribution of this function is then sub-

tracted from the signal and the process is repeated on

the residue. At the i-th iteration, it follows:



x i = 0

i−1

− α

m(i)

i > 0

(2)

where α

m(i)

is the weight associated to the optimum

atom g

m(i)

at the i-th iteration and r

is initialized

to x. Computing the orthogonal projections of r

i−1

on elements g

∈ D, the weight associated to each

dictionary element at the i-th iteration (vector α

) is

achieved:

i−1

, g

i−1

, g

= hr

i−1

, g

i (3)

Ruiz Reyes N., Vera Candeas P., J. Cañadas F., J. Carabias J., Cabañas P. and Rodriguez F. (2010).

MATCHING PURSUITS BASED ON PERCEPTUAL DISTORTION MINIMIZATION FOR SINUSOIDAL AUDIO MODELLING.

In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 97-102

DOI: 10.5220/0002917300970102

 SciTePress

The optimum atom g

m(i)

at the i-th iteration is ob-

tained by minimizing the residual energy:

m(i)

= arg min

∈D

= arg max

∈D

|α

| (4)

The matching pursuit algorithm (Mallat and

Zhang, 1993) is energy adaptive since the optimum

atom at each iteration is chosen by minimizing the

residual energy according to expression (4). However,

perceptual adaptation of the pursuit is desirable in or-

der to select the most perceptually important atom in-

stead the most correlated one with the current residue.

The main goal of this paper is to provide

a psychoacoustic based-sinusoidal audio modelling

method which deﬁnes a perceptual distortion mea-

sure using a linear model of the ear (S. Van de

Par and Heusdens, 2002). It must be stressed

that previous studies have already presented tech-

niques for psychoacoustic-adaptive matching pursuits

(Verma and Meng, 1999)(R. Heusdens and Kleijn,

2002)(Vera-Candeas et al., 2006). However, our

method deﬁnes a psychoacoustic stopping criterion

for the pursuit and also achieves a better separation

capability between tones and noise in sinusoidal au-

dio coding.

2 PERCEPTUAL DISTORTION

MEASURE

A perceptual adaptation of matching pursuits can be

achieved by deﬁning a perceptual distortion measure.

We have used the perceptual distortion measure intro-

duced in (S. Van de Par and Heusdens, 2002), which

is based on the monaural masking model described in

(T. Dau and Kohlrausch, 1996).

The model assumes that the auditory system can

be modelled by the scheme presented in Figure 1. As

can be seen, the signal is ﬁltered by the outer and mid-

dle ear response, h

, and then by an auditory ﬁlter

bank consisting of gamma-tone ﬁlters, h

. This ﬁl-

ter bank modelizes the behavior of the basilar mem-

brane within the inner ear. Let x denote the input au-

a u d i o s i g n a l

O u t e r a n d m i d d l e

e a r r e s p o n s e

F i l t e r b a n k

i n c r i t i c a l b a n d s

b a s i l a r m e m b r a n e

e x c i t a t i o n f o r

e a c h c r i t i c a l

b a n d

I n t e r n a l

c o m p o s i t i o n

a u d i t i v e

s e n s a t i o n

Figure 1: Model of the ear processing as a LTI system.

dio signal and d the distortion signal to be computed.

For each auditory band, a distortion can be measured.

This distortion is deﬁned as the relation between the

distortion energy and the signal energy at the b-th au-

ditory band (S. Van de Par and Heusdens, 2002),

PDM

(d) = C

||d

||x

(5)

where N is the signal length, ||x

the signal energy

at the output of the b-th auditory ﬁlter, ||d

the dis-

tortion energy at the output of this ﬁlter, C

the inter-

nal noise energy and C

a constant required for cali-

bration.

The total distortion can be computed as the sum of

all distortions for each auditory ﬁlter (S. Van de Par

and Heusdens, 2002), supposing that this sum corre-

sponds to the internal composition made to conform

the auditive sensation (see Figure 1). The perceptual

distortion measure is deﬁned as (S. Van de Par and

Heusdens, 2002),

PDM(d) = C

∑

PDM

(d) = C

∑

||d

||x

(6)

A distortion signal is therefore audible when its PDM

value is higher or equal than one.

3 PERCEPTUAL MATCHING

PURSUITS

In order to achieve a perceptual adaptation of match-

ing pursuits, the choice of the optimum atom has to

be modiﬁed taking psychoacoustic principles into ac-

count. Several methods have been presented in the

literature for such a goal (Verma and Meng, 1999)

(R. Heusdens and Kleijn, 2002)(Vera-Candeas et al.,

2006), all of them aiming to choose the most percep-

tually important atom at each iteration of the pursuit.

In standard energy-adaptive matching pursuit, the

optimum atom which minimizes the energy of the

residue is directly selected at each iteration. The main

idea about perceptual adaptation (Verma and Meng,

1999) is to modify the weights, aiming to take per-

ceptual principles into account. This idea can be ex-

pressed in the following way,

m(i)

= arg max

∈D

|α

perceptual

(7)

The perceptual weights in equation (7) can be de-

ﬁned by modifying the original weights with the help

of the masking threshold. In this way, Weighted

Matching Pursuits (WMP) are deﬁned in (Verma and

Meng, 1999). In (R. Heusdens and Kleijn, 2002),

Psychoacoustic-Adaptive Matching Pursuits (PAMP)

are deﬁned using a perceptual norm. This perceptual

SIGMAP 2010 - International Conference on Signal Processing and Multimedia Applications

norm is calculated as the integration of the ratio be-

tween the signal energy and the masking threshold

in the frequency domain. It deﬁnes a inner product

which facilitates the selection of the best matching

dictionary element in a perceptual point of view.

However, PAMP does not deﬁne a psychoacoustic

stopping criterion. The inner product does not offer

any information about if a selected tone is audible or

not. Furthermore, this problem can ﬁnd a worse sce-

nario, as stated in (R. Heusdens and Kleijn, 2002):

PAMP can select noisy energy as a tone when zero-

mean gaussian noise is present in the signal.

In our implementation, the main idea consists in

modifying standard matching pursuit so as to mini-

mize the perceptual distortion measure of the residue

at each iteration of the pursuit,

m(i)

= arg min

∈D

PDM(r

) (8)

The optimum atom according to equation (8) can

be computed applying the orthogonality property of

matching pursuits. Following a matching pursuit ap-

proach, the atoms are weighted by the coefﬁcients α

obtained from the correlation as is indicated in equa-

tion (3). Therefore, the residue at the i-th iteration can

be decomposed as r

i−1

= r

+ α

, fulﬁlling that r

and α

are orthogonals. Due to this orthogonality

property, the perceptual distortion measure of the r

i−1

residue in a matching pursuit approach can be written

PDM(r

i−1

) = PDM(r

) + PDM(α

) (9)

As a consequence, the minimization of the perceptual

distortion measure of the r

residue is the same than

maximizing the perceptual distortion measure of the

weighted atoms α

. Note that in a matching pur-

suits approach, the perceptual distortion PDM(r

i−1

)

is a constant at the i-iteration. Standard matching pur-

suit algorithm chooses at the i-th iteration the most

correlated atom with the residual r

i−1

in order to min-

imize residual energy. Expression (9) allows us to

state that choosing the weighted atom with the highest

perceptual distortion measure as the optimum atom,

the perceptual distortion measure of the r

residue at

the i-th iteration is minimized. Perceptual matching

pursuit computes the perceptual distortion measure

associated to each weighted atom and selects the atom

with the highest measure as the optimum atom at the

i-th iteration,

m(i)

= arg max

∈D

PDM(α

) (10)

Distortion signals to be measured at each iteration of

perceptual matching pursuit are the weighted atoms

. The perceptual distortion measure of weighted

dictionary elements at the i-th iteration is expressed

as,

PDM(α

) = C

∑





||x

(11)

The psychoacoustic stopping criterion can be di-

rectly deﬁned in our approach. The pursuit should be

halted at the iteration in which all perceptual distor-

tions are below one. Under this condition, all remain-

ing tones are assured to be inaudible. This condition

can be expressed as:

PDM(α

) ≤ 1, ∀g

∈ D (12)

The overcomplete dictionary D = {g

[n]} to be

considered for sinusoidal modelling is composed of

unit-norm complex exponentials.

4 RESULTS

First, we intend to illustrate the advantages of using

PDM(α

) based on a perceptual distortion mea-

sure against the inner products |α

PAMP

deﬁned in

(R. Heusdens and Kleijn, 2002).

Figure 2 shows the inner products |α

PAMP

and

the perceptual distortion measures PDM(α

), both

at the initial iteration, for a windowed input signal

composed of one tone plus noise. The tone power

is 19 dB above the density level of noise, the tone fre-

quency is 500Hz and the overcomplete dictionary is

composed of M = 4096 complex exponentials.

In this case, the PAMP approach does not select

the tone correctly because medium frequency noise

achieves more perceptual signiﬁcance than the tone

itself. As can be seen in the same ﬁgure, the PDM

approach performs a right tonal extraction.

The proposed psychoacoustic stopping criterion

performs correctly in this case, because after the ﬁrst

iteration all perceptual distortions are below 0 dB.

The better performance of our approach also hap-

pens when noise is added to a voicedspeech fragment.

Figure 3 illustrates the performance of the PAMP

approach when zero-mean white Gaussian noise is

added to a 23-ms voiced speech fragment, being 0

dB the signal-to-noise ratio. The magnitude of all ex-

tracted tones at each iteration is drawn in circles. As

can be seen, the maximum value of the perceptual in-

ner products is just below 2 KHz, which corresponds

to the most perceptually important sinusoid. This si-

nusoid is the ﬁrst one to be extracted, giving rise to

the plots in Figure 3(b). The left hand plot in Fig-

ure 3(b) also shows the magnitude and frequency of

the extracted tone at the ﬁrst iteration. It can be ob-

served on the right hand plot in Figure 3(b) that per-

ceptual distortion fall in the frequency region of the

MATCHING PURSUITS BASED ON PERCEPTUAL DISTORTION MINIMIZATION FOR SINUSOIDAL AUDIO

MODELLING

0 2 4 6 8 10

Frequency (KHz)

dB SPL

0 2 4 6 8 10

−20

−10

Frequency (KHz)

normalized dB

0 2 4 6 8 10

−20

−10

Frequency (KHz)

Figure 2: Perceptual inner products at the initial iteration

for PAMP approach (middle plot) and perceptual distortion

at the initial iteration for PDM approach (bottom plot) when

the analyzed signal consists of one tone plus white gaussian

noise. The tone power is 19 dB above the noise density

level. The top plot shows the energy spectrum of the input

signal (|R

( f)|

extracted tone at the previous iteration. Finally, Fig-

ure 3(c) shows the residue, extracted tones and inner

products at the ﬁfth iteration. As can be seen in the

left hand plot, four tones have been extracted, one of

them being a high frequency tone (close to 4 KHz)

that belongs to the noisy region of the signal. It can

also be seen that low frequency tones still remain in

the signal.

0 2 4 6 8 10

Frequency (KHz)

dB SPL

0 2 4 6 8 10

−50

−40

−30

−20

−10

Frequency (KHz)

normalized dB

0 2 4 6 8 10

Frequency (KHz)

dB SPL

0 2 4 6 8 10

−50

−40

−30

−20

−10

Frequency (KHz)

normalized dB

0 2 4 6 8 10

Frequency (KHz)

dB SPL

0 2 4 6 8 10

−50

−40

−30

−20

−10

Frequency (KHz)

normalized dB

(a)

(b)

(c)

Figure 3: (a) Energy spectrum of the residue R

( f) (energy

spectrum of the input signal) and perceptual inner products

for PAMP approach at the ﬁrst iteration when the analyzed

signal is a 23-ms voiced speech plus noise fragment, (b)

Idem at the second iteration and (c) Idem at the ﬁfth itera-

tion.

The results obtained by our approach when using

the same 23-ms voiced speech plus noise frame are

somewhat different. They are shown in Figure 4. The

magnitude of all extracted tones at each iteration is

drawn in circles. The second column of plot (d) sim-

ply shows the extracted tones after applying the stop-

ping criterion proposed in this paper. Now, the per-

ceptual distortion measure in the noisy region of the

spectrum is lower and, at the sixth iteration, the pur-

suit has not yet extracted a noisy tone, as happened

in the PAMP approach. All extracted atoms corre-

spond to sinusoids in the low frequency range (be-

low 2 KHz). Therefore, we can state that PDM-based

perceptual distortion computation provides higher ro-

bustness against modelling a noisy spectrum as a tone

at high frequencies than the PAMP-based approach.

This modelling mistake can provoke annoying sound

artifacts.

0 2 4 6 8 10

Frequency (KHz)

dB SPL

0 2 4 6 8 10

−10

Frequency (KHz)

0 2 4 6 8 10

Frequency (KHz)

dB SPL

0 2 4 6 8 10

−20

−10

Frequency (KHz)

0 2 4 6 8 10

Frequency (KHz)

dB SPL

0 2 4 6 8 10

−20

−10

Frequency (KHz)

0 2 4 6 8 10

Frequency (KHz)

dB SPL

0 2 4 6 8 10

Frequency (KHz)

dB SPL

(a)

(b)

(c)

(d)

Figure 4: (a) Energy spectrum of the residue R

( f) (energy

spectrum of the input signal) and perceptual distortions for

PDM approach at the ﬁrst iteration when the analyzed sig-

nal is a 23-ms voiced speech plus noise fragment, (b) Idem

at the second iteration, (c) Idem at the sixth iteration and (d)

Residue and extracted tones at the last iteration (9-th itera-

tion).

Finally, the operation of the psychoacoustic stop-

ping criterion for a 23-ms voiced speech signal plus

noise is shown in Figure 4. According to the pro-

posed stopping criterion, the pursuit is halted when

all perceptual distortions are below one (0 dB), which

happens at the 9-th iteration (the last iteration of the

pursuit in this example). Applying this criterion to

our example, all perceptually meaningful tones have

been extracted at the 9-th iteration. The psychoacous-

tic stopping criterion also help us to better discrim-

inate between tones and noise. It must be stressed

that frames where the noise power is meaningful will

only have a few perceptually relevant tones. In these

frames, the stopping criterion allows us to halt the al-

gorithm at a early iteration, avoiding that the pursuit

models a noisy region of the signal as a tone.

In order to compare the subjective behavior of

different deﬁnitions for perceptual matching pursuits,

each segment of the excerpts listed in table 1 is mod-

elled by choosing the 25 perceptually more relevant

tones. The signal to be rated corresponds to this si-

nusoidal part without quantization. The comparison

SIGMAP 2010 - International Conference on Signal Processing and Multimedia Applications

100

is based on rating the preference for the proposed

PDM-based approach versus PAMP (R. Heusdens and

Kleijn, 2002). CD-quality one-channel music and

speech signals taken from the set of excerpts used

in the MPEG standardization activities (ISO/MPEG,

2001) are chosen for testing. For comparison pur-

poses, the analysis/synthesis is done on a frame-by-

frame basis using a 50% overlap 23-ms Hanning win-

dow. A subjectivelistening test is performed using the

double blind triple stimulus methodology, in which

signal triplets OAB are presented to twelve experi-

enced listeners. Here, O is the original signal, while

A and B are the modelled signals using the PDM and

PAMP approaches, respectively. The results averaged

over all listeners for the 25 extracted sinusoids are

shown in table 1.

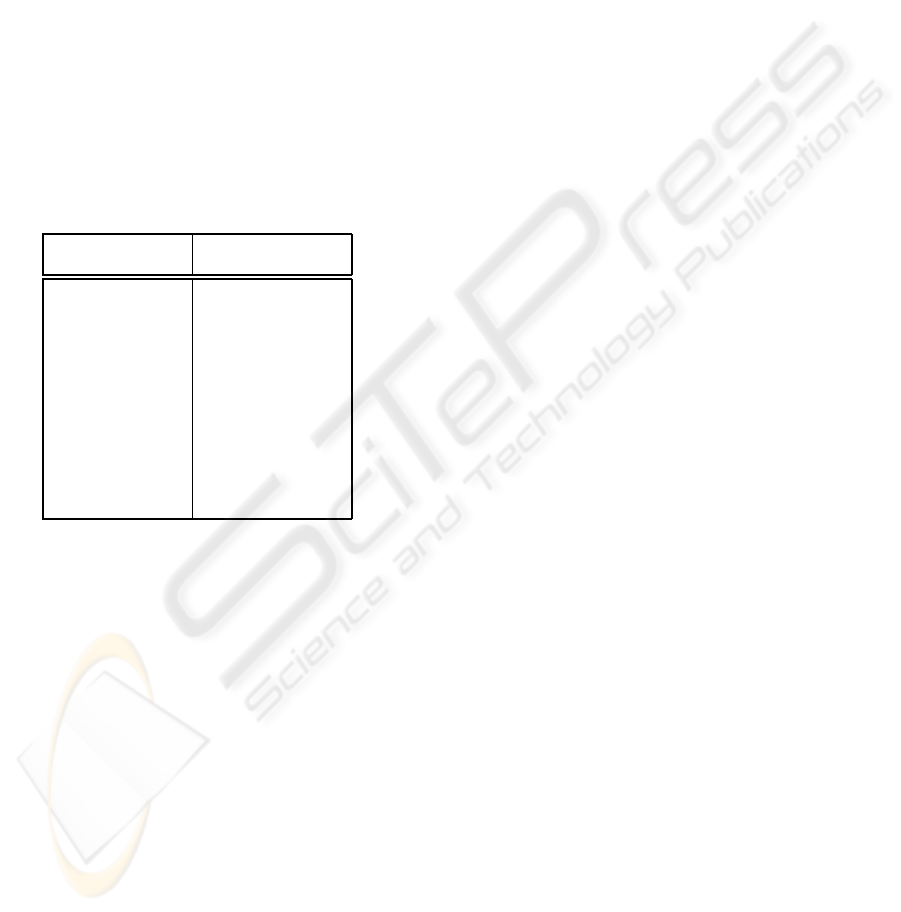
Table 1: Subjective listening tests. Signals are modelled

from the 25 most perceptually important sinusoids extracted

according to each approach.

Excerpt Preference (%)

for PDM-MP vs. PAMP

Suzanne Vega 75

German male speech 83

English female speech 100

Harpsichord 100

Castanets 58

Pitch pipe 42

Bagpipes 67

Glockenspiel 58

Plucked strings 100

Trumpet solo 67

Orchestra piece 100

Contemporary pop 100

As shown in table 1, PDM-based matching pur-

suit outperforms PAMP-based approach for most of

the signals taken for testing. The main reason for the

improvement is that PAMP sometimes extracts high

frequency components representing noise, which pro-

duces annoying sound artifacts (sharp sounds). This

effect is reduced with the proposed method, so that

a higher audio quality is achieved. However, the im-

provement regarding PAMP depends on the nature of

the audio signal. For those signals composed of tones

and noise with meaningful energy in high frequency,

such as English female speech, harpsichord, plucked

strings, orchestra and contemporary pop, all listeners

voted in favor of our approach. For the rest of the test

signals, the subjective differences are lower, because

these signals have less mixed components (tones and

noise) and both methods behave well.

5 CONCLUSIONS

This paper deals with the application of matching pur-

suits based on a perceptual distortion measure in or-

der to improve sinusoidal audio modelling. As shown

in the results, the proposed method achieves higher

perceptual quality for the synthesized signal than the

PAMP-based method when the number of frequencies

to be extracted is the same. Besides, the proposed per-

ceptual distortion measure allows us to deﬁne a per-

ceptual stopping criterion for the pursuit. Making use

of this stopping criterion, our approach has an impor-

tant advantage: higher protection (sturdiness) against

noise, mainly in high frequencies, which results in

a better balance between tones and noise. Matching

pursuit based on perceptual distortion minimization is

therefore a promising technique for sinusoidal audio

modelling, which allows to achieve high quality low

bit-rate audio coding and has interesting applications

as internet audio streaming.

ACKNOWLEDGEMENTS

This work was supported in part by the Spanish

Ministry of Education and Science under Project

TEC2009-14414-C03-02and the Andalusian Council

under project P07-TIC-02713.

REFERENCES

Goodwin, M. (1998). Adaptative signal models: theory,

algorithms and audio applications. Kluwer Academic

Publishers.

ISO/MPEG (2001). Call for proposal for new tools

for audio coding. ISO/IEC JTC1/SC29/WG11,

MPEG2001/N3793.

Mallat, S. and Zhang, Z. (1993). Matching pursuit with

time-frequency dictionaries. IEEE Transactions on

Signal Processing, 41:3397–3415.

McAulay, R. and Quatieri, T. (1986). Speech analy-

sis/synthesis based on a sinusoidal representation.

IEEE Trans. Acoustic, Speech and Signal Processing,

34(4):744–754.

MPEG, I. (2003). Avc test results validate superior technol-

ogy. In Technical report N6085.

R. Heusdens, R. V. and Kleijn, W. (2002). Sinusoidal mod-

eling using psychoacoustic-adaptive matching pur-

suits. IEEE Signal Processing Letters, 9(8):262–265.

S. Van de Par, A. Kohlrausch, G. C. and Heusdens, R.

(2002). A new psycho-acoustical masking model for

audio coding applications. In IEEE ICASSP’02, pages

1805–1808.

MATCHING PURSUITS BASED ON PERCEPTUAL DISTORTION MINIMIZATION FOR SINUSOIDAL AUDIO

MODELLING

101

T. Dau, D. P. and Kohlrausch, A. (1996). A quantitative

model of the ’effective’ signal processing in the audi-

tory system. J. Acoustic Society of America, 99:3615–

3622.

Vera-Candeas, P., Ruiz-Reyes, N., Cuevas-Martinez, J. C.,

Rosa-Zurera, M., and Lopez-Ferreras, F. (2006). Sinu-

soidal modelling using perceptual matching pursuits

in the bark scale for parametric audio coding. IEE

Proceedings on Vision, Image and Signal Processing,

153(4):431–435.

Verma, T. and Meng, T. (1999). Sinusoidal modeling using

frame-based perceptually weighted matching pursuits.

In IEEE ICASSP’99, pages 981–984.

SIGMAP 2010 - International Conference on Signal Processing and Multimedia Applications

102