
HEAP GARBAGE COLLECTION WITH REFERENCE COUNTING
Wuu Yang, Huei-Ru Tseng and Rong-Hong Jan
Computer Science Department, National Chiao-Tung University, Hsinchu, Taiwan, Republic of China
Keywords:
Closed cluster, Cyclic garbage, Depth-first search, Graph theory, Garbage collection, Reference count.
Abstract:
In algorithms based on reference counting, a garbage-collection decision has to be made whenever a pointer
x → y is about to be destroyed. At this time, the node y may become dead even if y’s reference count is not
zero. This is because y may belong to a piece of cyclic garbage. Some aggressive collection algorithms will
put y on the list of potential garbage regardless of y’s reference count. Later a trace procedure starting from
y will be initiated. Other algorithms, less aggressive, will put y on the list of potential garbage only if y’s
reference count falls below a threshold, such as 3. The former approach may waste time on tracing live nodes
and the latter may leave cyclic garbage uncollected indefinitely. The problem with the above two approaches
(and with reference counting in general) is that it is difficult to decide if y is dead when the pointer x → y
is destroyed. We propose a new garbage-collection algorithm in which each node maintains two, rather than
one, reference counters, gcount and hcount. Gcount is the number of references from the global variables and
from the run-time stack. Hcount is the number of references from the heap. Our algorithm will put node y on
the list of potential garbage if and only if y’s gcount becomes 0. The better prediction made by our algorithm
results in more efficient garbage collectors.
1 INTRODUCTION
Garbage collection algorithms can be classified into
two broad categories: (1) some algorithms mark all
live nodes and consider the rest as dead and (2) oth-
ers attempt to identify dead nodes directly. Tradi-
tional mark-sweep-compact collectors (Fischer and
LeBlanc, 1991) belong to the first category. This ap-
proach suffers from the long interrupt to normal com-
puter operations because the entire virtual memory
must be examined. Given today’s increasingly large
virtual memory, the interrupts become quite intolera-
ble.
Algorithms in the second category make use of
other information, mostly reference counts of various
kinds, to identify dead nodes directly (Collins, 1960;
Jones and Lins, 1996). Usually, there is a counter in
every node in the heap which keeps the number of ref-
erences that point to that node. When a node’s counter
falls to zero, it becomes a piece of garbage.
A problem with reference counting is that cyclic
garbage is difficult to collect. In addition to exam-
ining nodes’ counters, a part of the virtual memory
still needs to be scanned in order to identify cyclic
garbage.
In algorithms based on reference counting
(Collins, 1960; Jones and Lins, 1996; Lins et al.,
2007), a garbage-collection decision has to be made
whenever a pointer x → y is about to be destroyed. At
this time, the node y may become dead even if y’s ref-
erence count is not zero. This is because y may belong
to a piece of cyclic garbage.
The problem with the above two approaches (and
with reference counting in general) is that it is dif-
ficult to decide if y is dead when the pointer x → y
is destroyed. We propose a new collection algorithm
in which each node maintains two, rather than one,
reference counts, called gcount and hcount. Gcount
is the number of references from the global variables
and from the run-time stack. Hcount is the number
of references from the heap. Our algorithm will put
node y on the list of potential garbage if and only if
y’s gcount becomes 0. The better prediction made by
our algorithm results in more efficient garbage collec-
tors.
Our technique is locally complete in that it can
reclaim all the garbage that can be identified if a
garbage collector is limited to examine only the nodes
that are reachable from a given node. Our algorithm
will not cause a long interrupt to the normal com-
puter operation since it will examine a very limited
portion of a program’s run-time memory. Many such
267
Yang W., Tseng H. and Jan R. (2010).
HEAP GARBAGE COLLECTION WITH REFERENCE COUNTING.
In Proceedings of the 5th International Conference on Software and Data Technologies, pages 267-270
DOI: 10.5220/0002917502670270
Copyright
c
SciTePress

partial-scan algorithms (Christopher, 1984; Martinez
et al., 1990) focus on cyclic garbage, which often
make use of some cycle-detection techniques (Lin and
Hou, 2006; Lin and Hou, 2007; Lin, 2009). In con-
trast, our algorithm looks for closed clusters (to be
defined later) with two counters in each node. It is
not necessary to spend extra time to identify cyclic
structures.
Lins (Lins, 1992) extends Martinez et al.’s work
(Martinez et al., 1990) by searching for cyclic garbage
lazily. Redundant local searches are eliminated. Ba-
con et al. further incorporate concurrent search for
multiprocessor systems (Bacon et al., 2001; Bacon
and Rajan, 2001). It would be interesting to inves-
tigate a way to parallelize our algorithm.
The rest of this paper is organized as follows: Sec-
tion 2 gives a bird’s view of the heap during run time.
Our algorithm and an example are shown in Section
3. Section 4 gives a brief conclusion.
2 A BIRD’S VIEW OF THE
RUN-TIME HEAP
In this paper, we assume that the computer memory is
partitioned into two areas: the global area (which con-
tains global variables and the run-time stack) and the
run-time heap. The heap is partitioned into nodes. For
the sake of simplicity for presenting our algorithm, we
assume that no reference points to a node in the global
area.
Figure 1 shows a snapshot of a program’s run-time
memory at a certain instant. There are three nodes
A, B, and C in the global area. The nodes that are
reachable from A are classified into the following cat-
egories:
1. The P nodes are reachable only from A but not
from any other pointers in the global variables,
the stack, and the heap. When the reference in
A is destroyed, all P nodes become dead. The P
nodes corresponds to the subset {A}.
2. The Q nodes are reachable from A and some nodes
D in the heap. The Q nodes are unreachable from
from any other pointers in the global variables and
the stack. If D is actually dead, the associated Q
nodes are really P nodes. However, since most
dead nodes are not reclaimed immediately when
they become garbage, the Q nodes may remain un-
collected garbage for a period of time.
3. The R nodes are reachable only from A and B but
not from any other pointers in the global variables
and the stack. After the references in A and B are
Figure 1: Overview of garbage collection.
destroyed, all R nodes become dead. The R nodes
corresponds to the subset {A, B}.
4. The S nodes are reachable only from A and C but
not from any other pointers in the global area. The
S nodes corresponds to the subset {A,C}.
5. The T nodes are reachable from A, B, and C.
Similarly, the T nodes correspond to the subset
{A, B,C}.
When the reference in A is destroyed, for e.g.
when a new value is assigned to A, all the P nodes
become garbage. The Q nodes are reachable from D,
which is unclaimed garbage, and cannot be reclaimed
until D is reclaimed. Our garbage-collection algo-
rithm performs a few (possibly incomplete) depth-
first traversals, starting from node A, in order to free
all the P nodes. The P nodes constitutes the closed
cluster induced by node A, which is defined as fol-
lows (Yang et al., 2009).
Definition. The closed cluster induced by a node
n, denoted as CC(n), in a directed graph is the largest
set of nodes that are reachable from n but are not
reachable from any node outside the closed cluster.
3 OUR ALGORITHM
Our garbage-collection algorithm is shown in Figures
2 and 3.
During the execution of a program, garbage col-
lection may be activated several times. Because
information gathered in different garbage-collection
runs is mixed together, we use the global variable
currentrun to distinguish information gathered in dif-
ferent runs. This variable saves the trouble of erasing
the information after a collection run.
Each node y (in the heap) maintains two refer-
ICSOFT 2010 - 5th International Conference on Software and Data Technologies
268

1. global int currentrun := 0;
1. procedure CalculateCC(x : node)
2. currentrun := currentrun + 1;
3. d f sdead(x); /* x is the starting node, i.e., the root
of the dfs tree. */
4. hcount(x) := hcount(x) + 1;
5. search(x);
6. hcount(x) := hcount(x) − 1;
7. collect(x); /* The collect call is optional. */
8. end CalculateCC
1. procedure d f sdead(y : node)
2. if lastvisit(y) < currentrun then begin
3. /* This is the first visit to node y. */
4. lastvisit(y) := currentrun;
5. β(y) := 1;
6. if gcount(y) = 0 then begin
7. status(y) := dead; /* Assume y is dead
initially. */
8. for each outgoing edge of y (say y → z) do
d f sdead(z);
9. end
10. else begin /* gcount(y) > 0, which means y is
definitely live. */
11. status(y) := live;
12. for each outgoing edge of y (say y → z) do
d f slive(z);
13. end
14. else β(y) := β(y)+1; /* lastvisit(y) = currentrun
*/
15. end d f sdead
1. procedure d f slive(y : node)
2. if lastvisit(y) = currentrun and status(y) = live
then return;
3. lastvisit(y) := currentrun;
4. status(y) := live;
5. for each outgoing edge of y (say y → z) do
d f slive(z);
6. end d f slive
Figure 2: The CalculateCC algorithm.
ence counters: gcount and hcount. Gcount(y) con-
tains the number of references from the global area
to y. Hcount(y) contains the number of references
from the heap to y. Since our algorithm will perform
depth-first traversals in the heap, each node (in the
heap) may be visited more than once. Each node y
maintains a counter β(y), which records the number
of times y is visited during the depth-first traversal in
the current run of garbage collection.
Every node also contains a status variable, which
could be dead, live, or notvisitedyet. Every node
1. procedure search(y : node)
2. if status(y) = live then return;
3. if hcount(y) = β(y)
4. then /* y is a piece of garbage if not revived
later. */
5. for each child z of y in the dfs tree do
search(z);
6. else revive(y); /* hcount(y) > β(y) */
7. end search
1. procedure revive(y : node)
2. if status(y) = live then return;
3. status(y) := live;
4. for each outgoing edge of y (say y → z) do
revive(z);
5. end revive
1. procedure collect(y : node)
2. if status(y) = live then return;
3. for each child z of y in the dfs tree do collect(z);
4. f ree(y);
5. end collect
Figure 3: The CalculateCC algorithm (continued).
contains a lastvisit variable, which is the run number
when the node was visited for the last time.
When a pointer g → h is about to be deleted
and gcount(h) will become 0 after the deletion, h is
a candidate for garbage collection. The procedure
CalculateCC(h) will be invoked. The node h will be
called the root of the new run of garbage collection.
The set of nodes that are reachable from the root of
a collection run is called the span of the run. Note
that a complete depth-first traversal, starting from the
root, of a span will visit each edge in the span exactly
once. The traversal will high-light a depth-first tree
(dfs-tree) in the span. The span of the current run is
called the current span.
The CalculateCC(x) procedure first increments
currentrun, then calls d f sdead(x) to perform a depth-
first traversal, starting from node x, calls search(x)
to look for dead nodes, and finally calls collect(x)
to free the dead nodes. Because every node in the
dfs-tree except the root x has an incoming pointer,
hcount(x) is temporarily incremented by 1 before the
search(x) call. Hcount(x) is decremented by 1 after
the search(x) call.
Example. Figure 4 shows a snapshot of a com-
puter’s memory. The numbers under the node name
are the node’s gcount and hcount, respectively. For
instance, gcount(a) = 0 and hcount(a) = 2. Suppose
the edge q → a is about to be deleted. The garbage
collector CalculateCC(a) will invoke d f sdead(a).
d f sdead(a) will traverse the span, marking nodes
HEAP GARBAGE COLLECTION WITH REFERENCE COUNTING
269
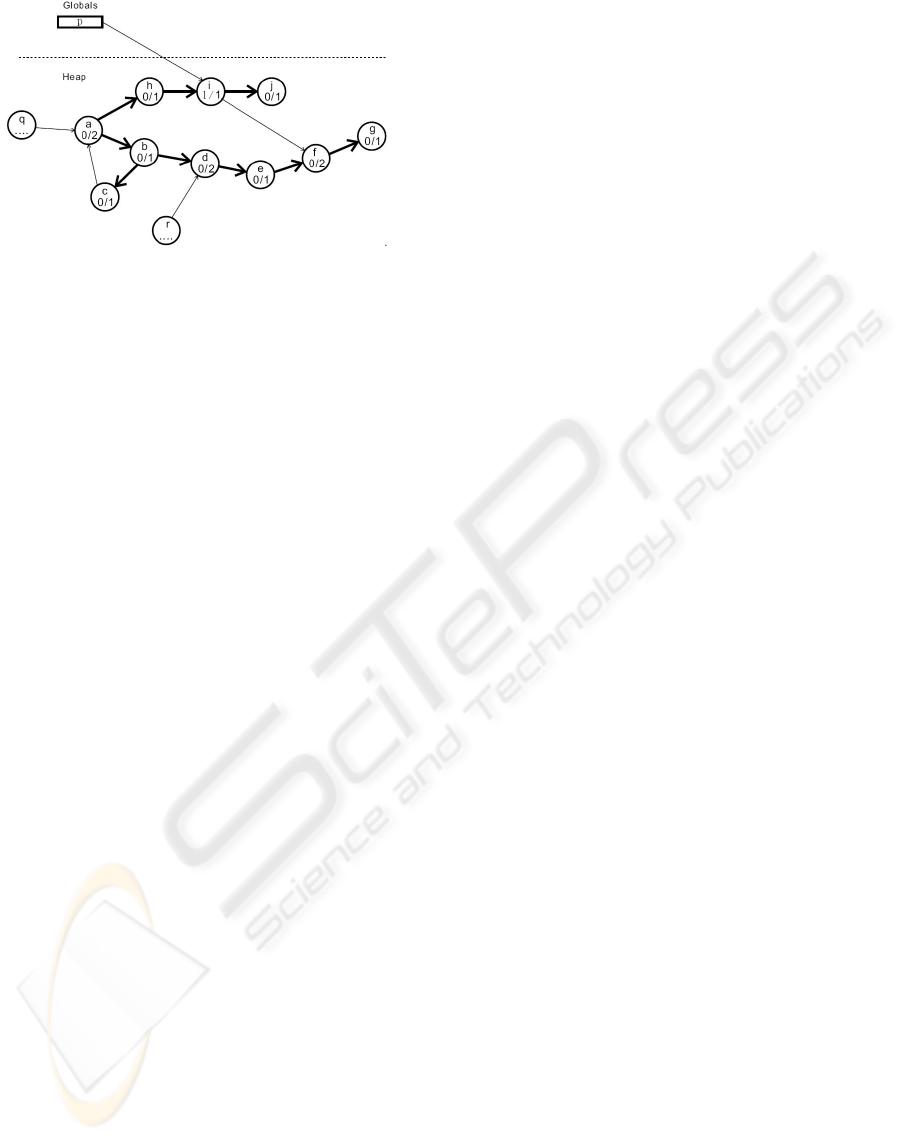
Figure 4: An example. The wide arrows form a depth-first-
search tree.
a, b, c, d, e, f , g, h (we assume that these nodes are vis-
ited in this order) as dead. When node i is visited,
d f slive(i) will be invoked since gcount(i) > 0. d f s(i)
will mark nodes i, j, f ,g as live. Note that nodes f
and g are visited in both d f sdead(a) and d f slive(i).
d f sdead and d f slive together will perform a com-
plete depth-first traversal plus some overlapped por-
tion in the span, which, in this example, contains
nodes f and g. The overlapped portion also depends
on the order nodes are visited during the d f sdead(a)
call.
4 CONCLUSIONS
We may save the root of a collection run in a buffer
and do not activate the garbage collector until a suf-
ficient number of roots have been accumulated. The
above algorithm may be adapted easily (Yang et al.,
2009).
Our new garbage-collection algorithm makes use
of two reference counters to better decide when a
node should be garbage-collected. It is better than
more aggressive algorithms by reducing the possibil-
ity of tracing live nodes and it is also better than less
aggressive algorithms because cyclic garbage is col-
lected sooner.
ACKNOWLEDGEMENTS
The work reported in this paper is partially supported
by National Science Council, Taiwan, Republic of
China, under grants NSC 96-2628-E-009-014-MY3,
NSC 98-2220-E-009-050, and NSC 98-2220-E-009-
051 and a grant from Sun Microsystems OpenSparc
Project.
REFERENCES
Bacon, D. F., Attanasio, C. R., Lee, H. B., Rajan, V. T.,
and Smith, S. (2001). Java without the coffee breaks:
A nonintrusive multiprocessor garbage collector. In
Proc. ACM SIGPLAN’01 Conf. Programming Lan-
guages Design and Implementation (PLDI).
Bacon, D. F. and Rajan, V. T. (2001). Concurrent cy-
cle collection in reference counted systems. In Proc.
15th European Conf. Object-Oriented Programming.
Springer-Verlag, LNCS 2072.
Christopher, T. W. (1984). Reference count garbage collec-
tion. Software Practice and Experience, 14(6):503–
507.
Collins, G. E. (1960). A method for overlapping and erasure
of lists. Communications of the ACM, 3(12):655–657.
Fischer, C. N. and LeBlanc, R. J. J. (1991). Crafting a Com-
piler with C. Benjamin/Cummings, MA.
Jones, R. E. and Lins, R. D. (1996). Garbage Collection
Algorithms for Dynamic Memory Management. John
Wiley and Sons, New York.
Lin, C. Y. (2009). Efficient Cyclic Garbage Reclamation
Appraoch for Reference Coounted Memory Manage-
ment Systems, Ph.D. Dissertation. National Cheng-
Kung University, Tainan, Taiwan, R.O.C.
Lin, C. Y. and Hou, T. W. (2006). A lightweight cyclic
reference counting algorithm. In Proc. Interna-
tional Conf. Grid and Pervasive Computing. Springer-
Verlag, LNCS 3947.
Lin, C. Y. and Hou, T. W. (2007). A simple and efficient
algorithm for cycle collection. ACM Sigplan Notices,
42(3):7–13.
Lins, R. D. (1992). Cyclic reference counting with
lazy mark-scan. Information Processing Letters,
44(4):215–220.
Lins, R. D., de Carvalho Junior, F. H., and Lins, Z. D.
(2007). Cyclic reference counting with permanent
objects. Journal of Universal Computer Science,
13(6):830–838.
Martinez, A. D., Wachenhauzer, R., and Lins, R. D. (1990).
Cyclic reference counting with local mark-scan. In-
formation Processing Letters, 34(1):31–35.
Yang, W., Tseng, H. R., and Jan, R. H. (2009). Identifying
closed clusters in the heap. Submitted for publication.
ICSOFT 2010 - 5th International Conference on Software and Data Technologies
270
