CONJUGATION AS PUBLIC KEY AGREEMENT PROTOCOL IN
MOBILE CRYPTOGRAPHY
Vittorio Ottaviani
Dipartimento di Informatica Sistemi e Produzione, Universit
`
a di Roma Tor Vergata, Via del Politecnico 1, 00133 Rome, Italy
Alberto Zanoni, Massimo Regoli
Centro “Vito Volterra”, Universit
`
a di Roma Tor Vergata, Via Columbia 2, 00133 Rome, Italy
Keywords:
Key agreement, Conjugation, Mobile Device.
Abstract:
We analyze a key agreement algorithm realization, not using Diffie-Hellman approach, but using matrix pow-
ers and conjugation. Introduced in a theoretical frame by Sakalauskas et. al. in 2007, it is here implemented
in J2ME on mobile devices (Nokia N70 equipped with Symbian S60 operating system). We study its appli-
ability and performances and compare them with Elliptic Curve and standard Diffie-Hellman Bouncy Castle
implementation, freely available on the web.
1 INTRODUCTION
Mobile devices diffusion increasing looks like a never
ending story; according to RBC analysts previsions
(Snol, 2009a), 2011 shipments of smartphone devices
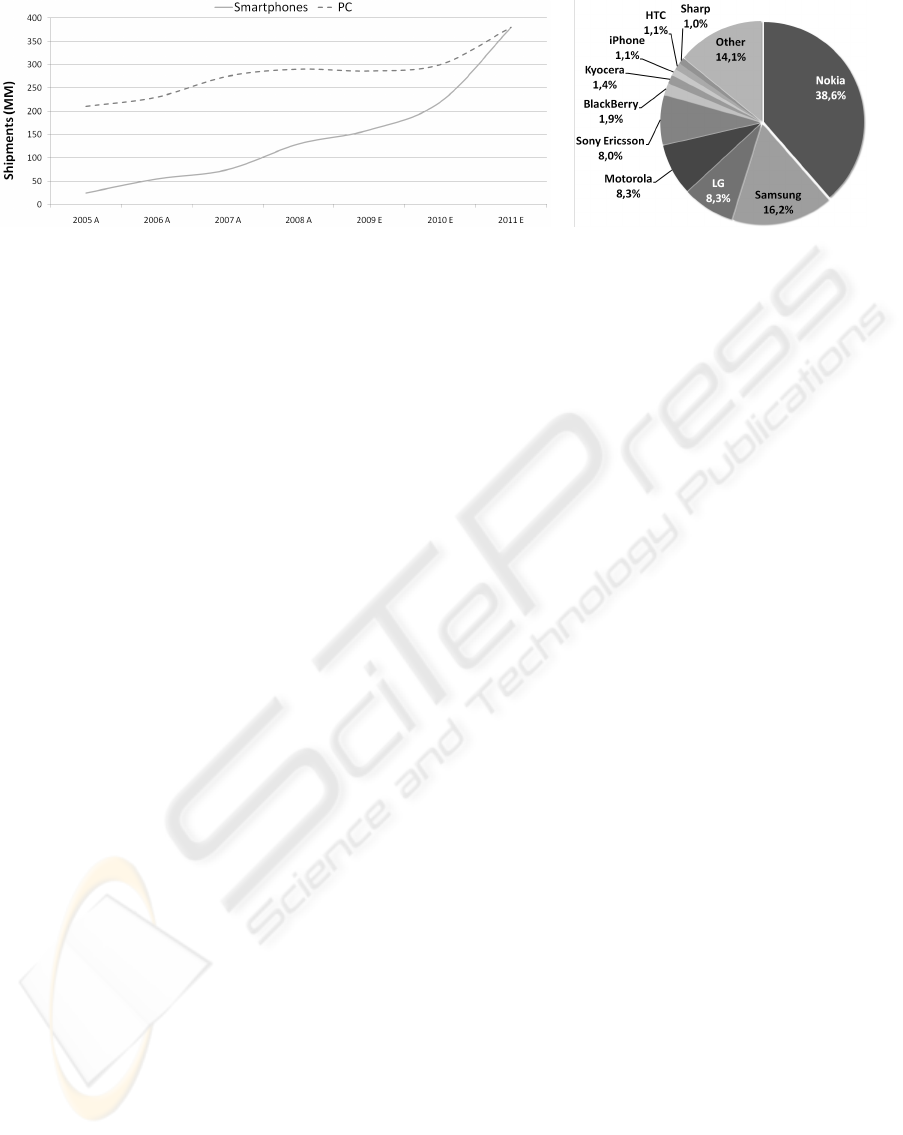
will approach 400 M units equalizing PC sales. Fig-
ure 1(a) resumes the trend 2005–2011, “A” indicates
actual values, “E” indicates estimated values.
Between vendors NOKIA still owns the biggest
part of the mobile device market, but other vendors,
e.g., Apple and RIM, are gaining considerable part
of the customers; Figure 1(b) shows the 2008 smart-
phone’s market situation (Snol, 2009b).
Smartphone OS’s diffusion, obviously, reflects the
smartphone device diffusion; Symbian leads the mar-
ket with 52% followed by RIM 17%, Windows Mo-
bile 12%, iPhone 8%, Palm 2%, Android 1% and oth-
ers 9% (Dignan, 2009).
As more and more powerful smartphones and the
like are becoming everyday matter, many software ap-
plications are appearing on the market. Multimedia
management, games, navigators, chat programs and
message exchange are only some examples of the pos-
sibilities that these devices can be used for.
For more delicate matters (e.g., mobile banking,
payments and other operations that require privacy
and security for the user, like mobile voting systems),
cryptographic protocols and algorithms enter the
game. In particular, in many cases a key agreement
is needed to send/exchange private data/information
by coding them with a specific algorithm. Some mo-
bile cryptography use examples are (Ahmad et al.,
2009), in which elliptic curves are efficiently used,
and (Grillo et al., 2008a), (Grillo et al., 2008b), con-
cerning trusted text messaging. All these works focus
more on coding/signing part than on key agreement,
but of course a key agreement phase is needed before
encrypting or signing.
In this paper we present a JavaME implementa-
tion of a new key agreement protocol – a particu-
lar case of a class recently proposed in (Sakalauskas
et al., 2007) – and compare our implementation per-
formance (Ottaviani et al., 2009) against standard and
Elliptic Curve Diffie-Hellman protocol (Diffie and
Hellman, 1976).
In the next section we explain the mathematical
problem to be solved to exploit the key agreement,
and some consideration upon possible attacks and
why these attacks are not effective on such algorithm.
In section 3 the implementation choices are presented,
analyzing why they do not affect security, optimiz-
ing performances. In section 4 we analyze the test-
ing methodology explaining each step of the testing
phase. Section 5 shows the testing phase results. Sec-
tion 6 analyzes with more detail the section 5 data.
Section 7 resumes all results proposing possible im-
provements and applications of the algorithm.
411
Ottaviani V., Zanoni A. and Regoli M. (2010).
CONJUGATION AS PUBLIC KEY AGREEMENT PROTOCOL IN MOBILE CRYPTOGRAPHY.
In Proceedings of the International Conference on Security and Cryptography, pages 411-416
DOI: 10.5220/0002917904110416
Copyright
c
 SciTePress

(a) (b)
Figure 1: (a) Smartphone and PC sales prevision, (b) 2008 mobile handset market share.
2 MATHEMATICAL SETTING:
KEY AGREEMENT PROTOCOL
We consider GL(d, Z
p
) = M , where p is a prime
number. Fix G ∈ M and let ϕ be the conjugation iso-
morphism associated to G
ϕ
G
: M 3 M 7→ ϕ
G
(M) = GMG
−1
∈ M
The following public key agreement between Alice
(A) and Bob (B) – see (Sakalauskas et al., 2007)
for a more general setting – exploits the property
[ϕ
G
(A)]
n
= ϕ
G
(A
n
).
1. A and B share Q, S ∈ M , with SQ 6= QS and
det(Q) = |Q| = 1,
2. A chooses two numbers x
A
, n
A
∈ N.
3. A computes M
A
= S
n
A
Q
x
A
S
−n
A
and sends it to B.
4. B receives from A the matrices M
A
.
5. B chooses two numbers x
B
, n
B
∈ N, computes
M
B
= S
n
B
Q
x
B
S
−n
B
and sends M
B
to A.
6. A computes M
AB
= S
n
A
M
x
A
B
S
−n
A
=
S
n
A
(S
n
B
Q
x
B
x
A
S
−n
B
)S
−n
A
7. B computes M
BA
= S
n
B
M
x
B
A
S
−n
B
=
S
n
B
(S
n
A
Q
x
A
x
B
S
−n
A
)S
−n
B
At the end A and B share the common matrix
M
AB
= M
BA
, which represents the Secret Shared Key
(SSK). Infact,
M
AB
= S
n
A
+n
B
Q
x
B
x
A
S
−(n
A
+n
B
)
= S
n
B
+n
A
Q
x
A
x
B
S
−(n
B
+n
A
)
= S
n
B
M
x
B
A
S
−n
B
= M
BA
Note that if |Q| 6= 1, a possible eavesdropper Eve (E)
could set up a discrete logarithm problem by consid-
ering the determinantal equation (Bodrato, 2009)
|M
A
| = |S
n
A
Q
x
A
S
−n
A
| = |S
n
A
||Q
x
A
||S
−n
A
|
= |S|
n
A
|Q|
x
A
|S|
−n
A
= |Q|
x
A
with det(Q) known, if E can solve this scalar discrete
logarithm problem, thus recovering x
A
, then she can
easily find, by solving a linear problem, and adjusting
the free parameters entering in the solution, a polyno-
mial X in the matrix S of degree ≤ d, with coefficients
in Z
p
such that M
A
X = XQ
x
A
.
Using this, E can compute
XM
x
A
B
X
−1
= (XS
n
B
X
−1
)(XQ
x
A
X
−1
)
x
B
(XS
−n
B
X
−1
)
= S
n
B
M
x
B
A
S
−n
B
= M
AB
because X commutes with S. In conclusion: if
det(Q) 6= 1, then, the breaking complexity of the al-
gorithm is essentially equivalent to the breaking com-
plexity of a (discrete) logarithm in Z
p
, i.e., to that of
(scalar) Diffie-Hellman. With det(Q) = 1 (see step
1 of agreement process), this “attack” cannot be per-
formed.
Figure 2 shows the agreement process performed
by the algorithm. E could intercept S, Q, d, p, M
A
and
M
B
. In order to recover the private keys (e.g., n
A
and
x
A
), she could set up the following equation
M
A
= S
n
A
Q
x
A
S
−n
A
= (S
n
A
QS
−n
A
)
x
A
but this is much more difficult than a usual matrix dis-
crete logarithm problem (DLP), as the base matrix is
unknown. Other identities, such as
M
A
S
n
A
= S
n
A
Q
x
A
are difficult to exploit because both S
n
A
and Q
x
A
are
not known separately.
We have that
#
M =
∏
d−1
i=0
(p
d
− p
i
). Let o(M) be
the order of a matrix M ∈ M , i.e., the smallest integer
such that M
o(M)
= 1. In order to avoid useless compu-
tations, it is sufficient to choose n
A
, n
B
< o(S) (resp.
x
A
, x
B
< o(Q)).
The order of a matrix M ∈ M is in general difficult
to compute, but an upper bound for it can be found as
follows. For each M ∈ M let p
M
(x) =
∏
k
i=1
f
i
(x)
d
i
be
its characteristic polynomial factorized in Z[x], with
SECRYPT 2010 - International Conference on Security and Cryptography
412

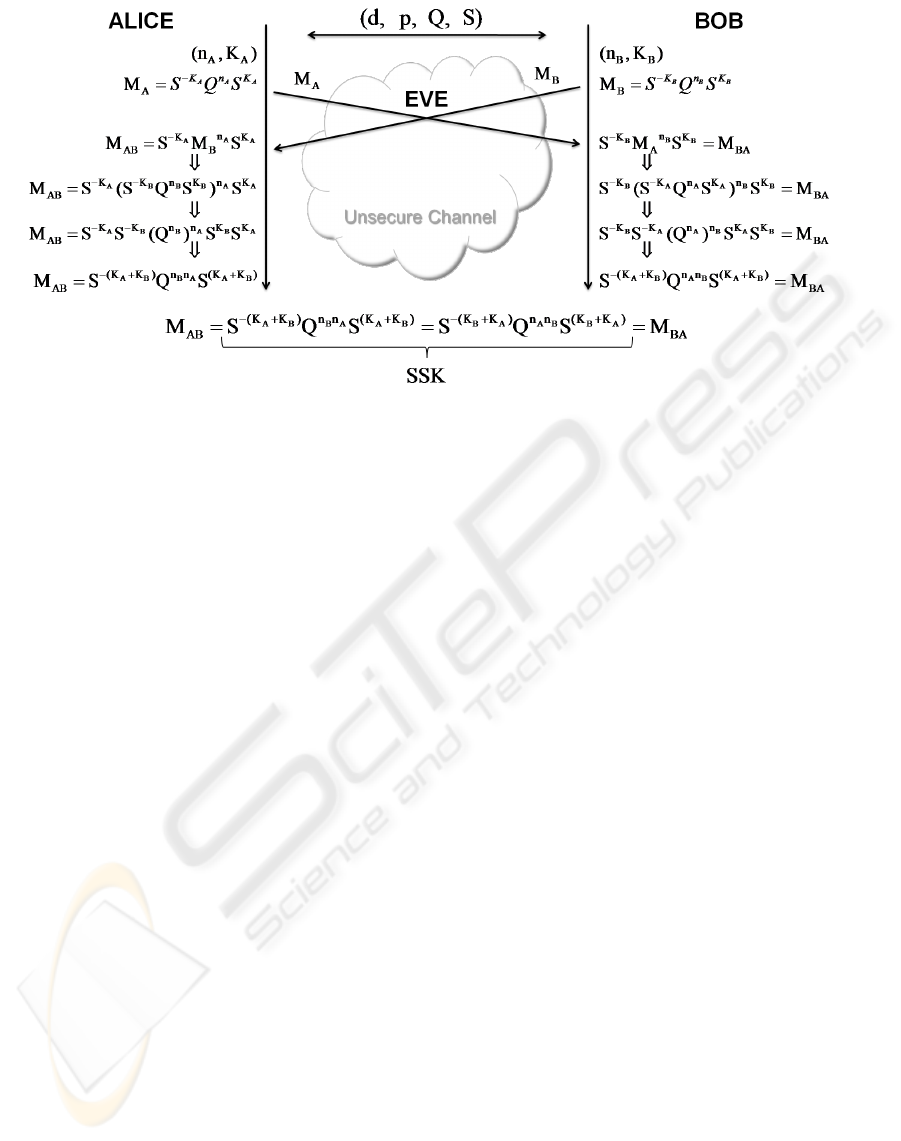
Figure 2: Key Agreement process using conjugate.
α = max{d
i
| i = 1, . . . k}. An upper bound (multiple)
m(M) for its multiplicative order o(M) is given by the
following formula (Celler and Leedham-Green, 1995)
m(M) = lcm(p
d
1
− 1, . . . , p
d
k
− 1) · p
dlog
p
(α)e
3 J2ME IMPLEMENTATION
The previously described operations to perform key
agreement have been developed in Java Micro Edition
(J2ME). We chose to implement in such programming
language because we need a suite that can run on
different hardware platforms and operating systems.
Moreover we noticed that a good performance evalu-
ation can be obtained, comparing our implementation
of the key agreement algorithm with Bouncy Castle’s
implementation of Elliptic Curve and standard Diffie-
Hellman key agreement algorithm.
Bouncy castle provide a plethora of API per-
forming different cryptographic operations imple-
mented in JAVA, J2ME and C#, we used the El-
liptic Curve Diffie-Hellmen (ECDH) and the stan-
dard Diffie-Hellman (DH) key agreement J2ME im-
plementation to perform the comparison. The first
step to implement the algorithm described in section
2, is to implement the modular operations on matri-
ces (e.g., modular matrix multiplication, power, in-
version, conjugate and other ancillary operations).
It is very important, in a mobile environment, to
optimize every step of every operation with respect
to resource consumption: in small capacity devices
every waste of resources implies a delay, larger than
the delay, in more performing devices corresponding
to the same waste: because of the shortage of RAM,
CPU and storage capacity, operations need to be opti-
mized as much as possible.
To perform the operations described in section 2
we use a 32 bit unsigned integer data structure. Un-
fortunately in JAVA and J2ME there is no unsigned
integer data structure; to solve this problem there are
two possible approaches:
1. use bigger data structures, such as 64 bit signed
long integer simulating a 32 bit size applying
modulus when the value exceeds 2
32
,
2. use available 32 bit signed integer combining it
with arithmetical operations modulus 2
31
.
We have chosen the latter solution, i.e., to develop
the modular matrix as a integer array (int[ ]) with
modulo 2
31
. This data structure is, in our opinion,
the best compromise between RAM wasting and CPU
usage due to operations needed to perform a task. Se-
curity of the key agreement is not affected using 31
bit integers, while performances are compromised, if
one uses the 64 bit signed integer to simulate 32 bit
unsigned integer. Using long integers the RAM con-
sumption doubles and the system’s performances, in
our opinion, degrade too much to justify the slight im-
provement in security.
4 PERFORMANCE TESTING
METHODOLOGY
In this section we report our performance tests of Ma-
trix Conjugation Based Key Agreement versus Ellip-
tic Curve and standard Diffie-Hellman on a Nokia
N70 platform.
CONJUGATION AS PUBLIC KEY AGREEMENT PROTOCOL IN MOBILE CRYPTOGRAPHY
413

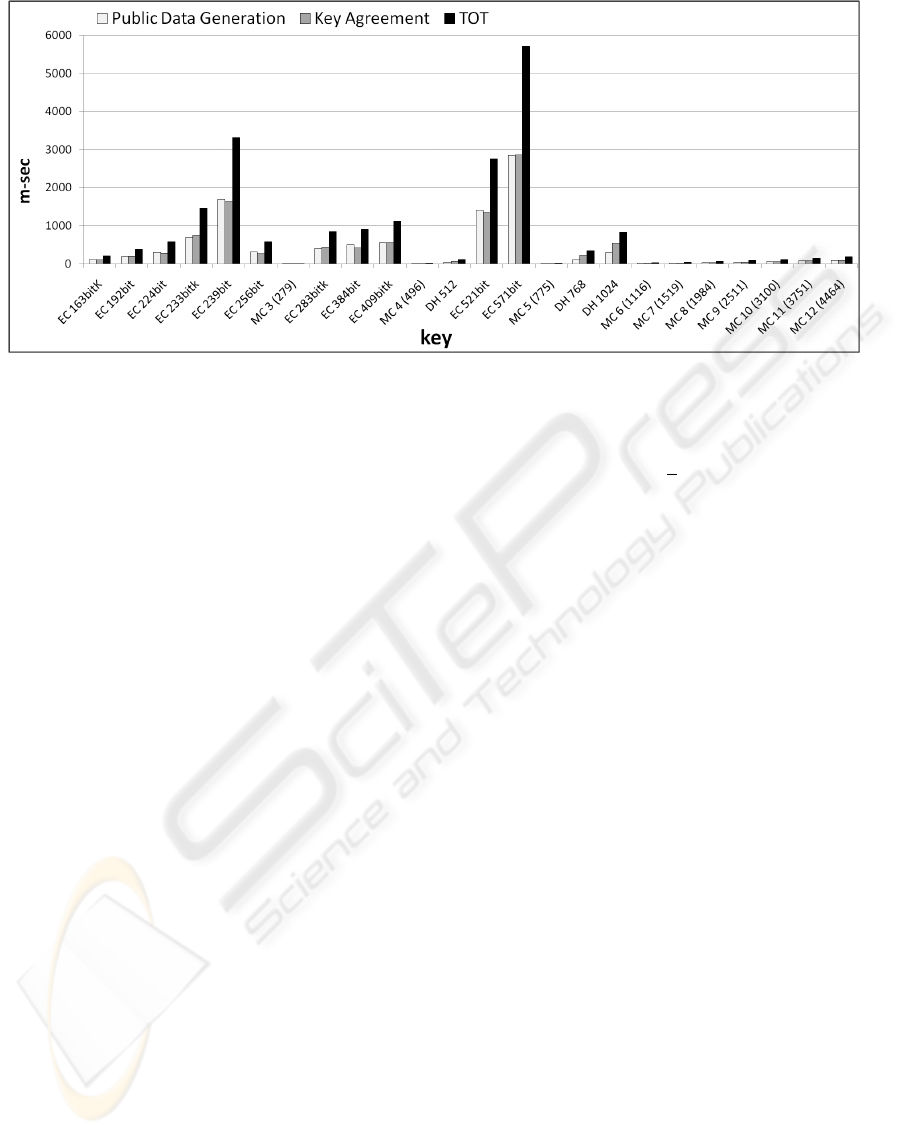
Figure 3: Public data and Key Agreement generation time: all tests. EC . . . bit: Elliptic Curve Diffie-Hellman with a . . . bit
key. EC . . . bitK: Koblitz Elliptic Curve Diffie-Hellman with a . . . bit key. MC d (. . . ): Matrix Conjugation at dimension d
with a . . . bit key. DH . . . : Diffie-Hellman with a . . . bit key
The NOKIA N70 is a multimedia smartphone
launched in Q3 2005. In 2007, it was the second most
popular cellular phone, with 8% of all sales at Ram-
pal Cellular Stockmarket(PRNewswire, 2007). Our
experiments show similar results with other mobile
devices. NOKIA N70 is equipped with:
• CPU : Texas Instruments OMAP 1710 (ARM ar-
chitecture 926TEJ v5) 220 MHz processor
• RAM : 55 MB
• FLASH : 19.9 MB
• MMC : 2 GB
• SCREEN : 176×208 TFT Matrix, 256K colours
• BATTERY : BL-5C (970 mAh)
• OS : BB5 / Symbian OS v8.1a, S60 Platform Sec-
ond Edition, Feature Pack 3 operating system
• JAVA : MIDP 2.0 midlets
In a mobile device, in general, and using J2ME, in
particular, there are several problems in measuring the
time required for a given task, because the accuracy of
the System.currentTimeMillis() function is not
sufficient.
We will use, as an estimate of the time length of
a given task, the avarage of the time lengths, mea-
sured on several repetitions of the same task. More
precisely:
Definition 1. Let n be the number of itera-
tions of one task, and let θ
i
denote the time
needed to perform the i
th
task measured using the
System.currentTimeMillis(). The actual time
that the device needs to perform such task will be
measured as follows:
Θ
n
=
1
n
n
∑
i=1
θ
i
(1)
It is an empirical fact that Θ
n
becomes approxi-
mately independent from n, for “large” n. The size on
n depends on the task is and usually smaller for longer
tasks (i.e., larger Θ
i
) , see Table 1 below.
For each algorithm tested, we performed the
above described operation for the most used instances
of the algorithms; e.g., for the ECDH case we tested
all the curves recommended by the NIST (NIST,
1999). For what concerns standard Diffie-Helman and
Matrix Conjugation Based Key Agreement analysis,
we considered instances with comparable private key
length, in order to have an idea of brute force attack
complexity with respect to performances.
Next section shows the experimental results of the
comparison of various performances of different key
agreement algorithms.
5 PERFORMANCE EVALUATION
Here we show the results of all the tests performed on
standard key agreement algorithms and protocols and
on Matrix Conjugation Based Key Agreement.
We compared the performance of Matrix Conju-
gation Based Key Agreement to other reference algo-
rithms, such as Diffie-Hellman key agreement (DH)
(Rescorla, 1999) and Elliptic Curve Diffie-Hellman
key agreement (ECDH) (Barker et al., 2007). We re-
mark that these algorithms are the most used to per-
form key agreement operations in desktop and mo-
bile environments. Among the NIST suggested Ellip-
tic Curves (Research, 2000), we select both Koblitz
SECRYPT 2010 - International Conference on Security and Cryptography
414

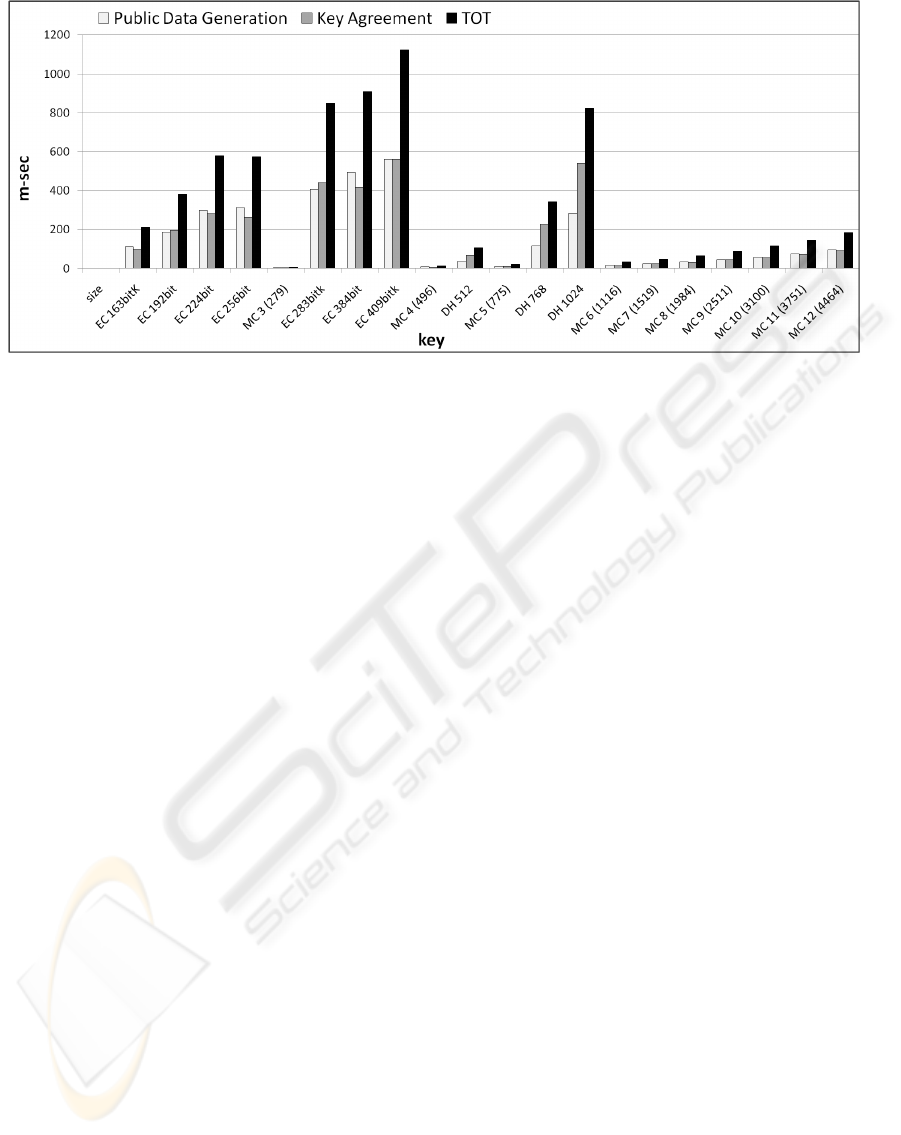
Figure 4: Public data and Key Agreement generation time: results with an upper bound of 1 sec. EC . . . bit: Elliptic Curve
Diffie-Hellman with a . . . bit key. EC . . . bitK: Koblitz Elliptic Curve Diffie-Hellman with a . . . bit key. MC d (. . . ): Matrix
Conjugation at dimension d with a . . . bit key. DH . . . : Diffie-Hellman with a . . . bit key.
curves (ending with a K in Figure 3 and Figure 4) and
pseudo-random curves over GF(p).
In Figure 3 the time comparison between Matrix
Conjugation Based Key Agreement (MC in Figure
3 and Figure 4), standard and Elliptic Curve Diffie-
Hellman is shown. We can note that conjugation
based key agreement generates the public data and the
SSK faster than the other algorithms. Since in Fig-
ure 3 the difference in generation times for the secret
and the key agreement is not really significant, we il-
lustrate in Figure 4 a closer look to show better the
differences in time.
While a key agreement using Elliptic Curve with a
571-bits key takes 5706.3 milliseconds, a key agree-
ment using conjugation based key agreement with a
5 × 5 matrix (775-bits key) takes only 20.63 millisec-
onds. This difference is significant even consider-
ing that the SSK generated by Matrix Conjugation
Based Key Agreement is 50% larger than the Elliptic
Curve SSK. Even when considering the case of stan-
dard Diffie-Hellman, the differences in mobile envi-
ronment look quite impressive; for example, a Diffie-
Hellman 768-bits SSK is agreed in 343.44 millisec-
onds while a Matrix Conjugation Based Key Agree-
ment 775-bits SSK takes only 20.63 milliseconds.
These differences are illustrated in Figure 4.
6 EXPERIMENTAL RESULTS
Table 1 summarizes all the results obtained in the
performance testing for the different classes of algo-
rithms. Parameters field indicates:
• In the ECDH case, the type of curve that is used
to generate the agreement (K indicates a Koblitz
curve) and the size of the generated SSK;
• In the DH case, the size of the generated SSK;
• In the Matrix Conjugation Based Key Agreement,
the matrix dimension and the bit size of the matrix
generated as key.
Public Data Generation (Pub. Data) field indicates
the time to generate the exchanged data to agree a
SSK. The field Key Agreement (Key Agr.) shows time
needed to generate the SSK by means of exchanged
and private data.
In Total field the sum of times used to generate ex-
changed data and SSK is shown. The last field, Itera-
tions (Iter.), indicates how many times the agreement
has been performed. This field is useful to understand
the accuracy of the values in the Public Data Gen-
eration, Key Agreement and Total fields. In all cases
but ECDH we did 100 iterations; in ECDH cases we
decided to use just 10 iterations because times were
more than one order of magnitude bigger than in the
other cases, so that keeping the same accuracy was
not necessary.
7 CONCLUSIONS
In this paper we compared a custom key agree-
ment algorithm based on matrix conjugation with
standard Diffie-Hellman and Elliptic Curve Diffie-
Hellman key agreement. Our experiments have been
performed using one of the most popular smartphone
in the world. Experimental results showed that the
key agreement based on matrix conjugation results to
CONJUGATION AS PUBLIC KEY AGREEMENT PROTOCOL IN MOBILE CRYPTOGRAPHY
415

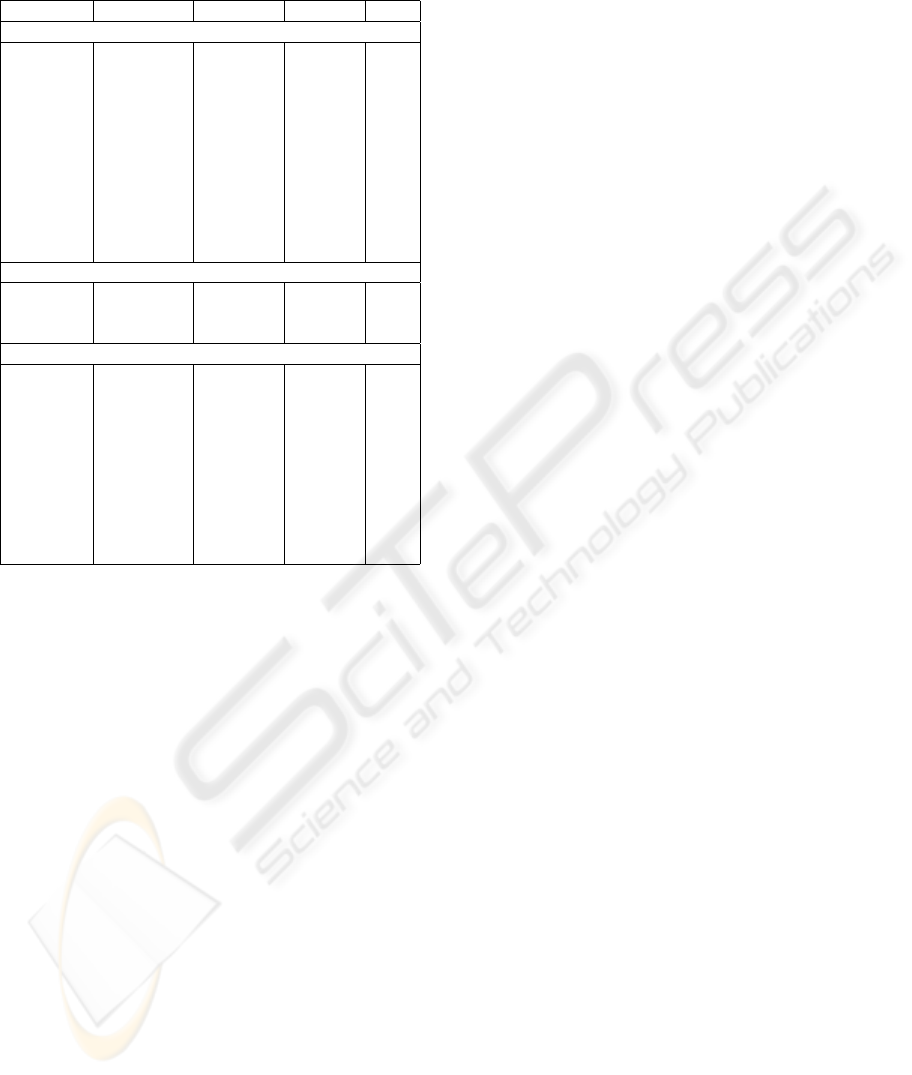
Table 1: Time used from algorithms to generate the secret
to agree a SSK.
Param. Pub. Data Key Agr. Total Iter.
Elliptic Curve Diffie-Hellman
163bit K 110,90 100,00 210,90 10
192bit 185,90 195,30 381,20 10
224bit 298,50 281,20 579,70 10
233bit K 696,90 759,30 1456,20 10
239bit 1684,40 1626,60 3311,00 10
256bit 312,50 262,50 575,00 10
283bit K 407,80 442,20 850,00 10
384bit 493,70 415,70 909,40 10
409bit K 561,00 560,90 1121,90 10
521bit 1404,60 1342,20 2746,80 10
571bit 2845,30 2861,00 5706,30 10
Diffie-Hellman
512 37,51 68,58 106,09 100
768 116,25 227,19 343,44 100
1024 282,98 539,83 822,81 100
Matrix Conjugation Based Key Agreement
3 (279) 3,27 3,13 6,40 100
4 (496) 6,72 5,94 12,66 100
5 (775) 10,32 10,31 20,63 100
6 (1116) 16,72 15,47 32,19 100
7 (1519) 23,76 22,96 46,72 100
8 (1984) 33,90 31,41 65,31 100
9 (2511) 44,35 44,85 89,20 100
10 (3100) 57,97 56,87 114,84 100
11 (3751) 74,21 71,26 145,47 100
12 (4464) 93,91 89,53 183,44 100
be from 8 to 450 times faster than the two DH.
Providing the users new services on their mobile
device enlarges the need of security to protect the in-
formation exchanged; such information can contain
data about bank accounts, credit card numbers, pins
or simply passwords.
Currently existing cryptographic methods affect
too much usability of applications, charging the sys-
tem with resource consumption due to cryptographic
operations. Considering the growing business oppor-
tunity around the mobile world and, at the same time,
the need of new more performing applications that
can run on small capacity devices, as smartphones or
netbooks, this work’s results open the possibility to
apply such cryptographic methodology to many sce-
narios in mobile devices use and to continue working
in the development of innovative cryptographic meth-
ods based on new ideas.
REFERENCES
Ahmad, T., Hu, J., and Han, S. (2009). An efficient mobile
voting system security scheme based on elliptic curve
cryptography. Network and System Security, Interna-
tional Conference on, 0:474–479.
Barker, E., Johnson, D., and Smid, M. (2007). NIST SP
800-56A - Recommendation for Pair-Wise Key Estab-
lishment Schemes Using Discrete Logarithm Cryptog-
raphy. NIST.
Bodrato, M. (2009). Personal communication.
Celler, F. and Leedham-Green, C. R. (1995). Calculating
the order of an invertible matrix. In In Groups and
Computation II, pages 55–60. American Mathemati-
cal Society.
Diffie, W. and Hellman, M. E. (1976). New directions in
cryptography. IEEE Transactions on Information The-
ory, IT-22(6):644–654.
Dignan, L. (2009). Smartphone operating systems: The
market share, usage disconnect.
Grillo, A., Lentini, A., Me, G., and Italiano, G. F. (2008a).
Transaction oriented text messaging with trusted-sms.
In ACSAC, pages 485–494. IEEE Computer Society.
Grillo, A., Lentini, A., Me, G., and Rulli, G. (2008b).
Trusted sms - a novel framework for non-repudiable
sms-based processes. In Azevedo, L. and Londral,
A. R., editors, HEALTHINF (1), pages 43–50. IN-
STICC - Institute for Systems and Technologies of In-
formation, Control and Communication.
NIST (1999). Recommended elliptic curves for federal gov-
ernment use. Technical report, NIST.
Ottaviani, V., Italiano, G. F., Grillo, A., and Lentini, A.
(2009). Benchmarking for the qp cryptographic suite.
Technical report, University of Rome “Tor Vergata”,
dept. of Informatics, Systems and Production.
PRNewswire (2007). Rcs announces 2007 January-June
trading data for the global cellular phone open mar-
ket. Note.
Rescorla, E. (1999). Rfc 2631 - Diffie-Hellman key agree-
ment method. Technical report, RTFM Inc.
Research, C. (2000). Standards for efficient cryp-
tography - SEC 1: Elliptic curve cryptogra-
phy. Technical Report 20, Certicom Corp., secg-
[e-mail].
Sakalauskas, E., Tvarijonas, P., and Raulynaitis, A. (2007).
Key agreement protocol (kap) using conjugacy and
discrete logarithm problems in group representation
level. Informatica, 18(1):115–124.
Snol, L. (2009a). More smartphones than PCs by 2011. PC
Advisor, August 2009.
Snol, L. (2009b). Smartphones racing past boring mobiles.
PC Advisor, August 2009.
SECRYPT 2010 - International Conference on Security and Cryptography
416