
EVALUATION OF FEEDBACK AND FEEDFORWARD
LINEARIZATION STRATEGIES FOR AN ARTICULATED ROBOT
Roland Riepl, Hubert Gattringer and Hartmut Bremer
Institute for Robotics, Johannes Kepler University, Altenbergerstr. 69, 4040 Linz, Austria
Keywords:
Robotics, Nonlinear control, Decentralized control, Linearization, Multi-body dynamics, Identification.
Abstract:
The increasing demand of high performance applications in industrial environments calls for improved control
strategies for nonlinear mechanical systems. Common flatness based approaches, effectively linearizing a
highly nonlinear system, are available and ready for deployment. This contribution focuses on evaluating
these strategies in a modern and widely used industrial setup.
1 INTRODUCTION
The objective to reduce cycle times while increasing
the tool center point precision and dynamics, espe-
cially in robotic applications, requires sophisticated
motion control.
Robots with a high number of degrees of freedom,
for example articulated robots, are complex machines.
Their system dynamics may be described by the equa-
tions of motion, a set of highly nonlinear differen-
tial equations. In contrary to the common approach,
using Lagrange equations of second kind, this con-
tribution utilizes the projection equation in subsys-
tem representation, well described in (Bremer, 2008).
Next to commonly used decentralized proportional
and derivative (PD) control schemes, different model-
based linearization techniques exist, as (Isidori, 1985;
Slotine and Li, 1990; Fliess et al., 1995; Khalil and
Dombre, 2004) suggest. These methods effectively
linearize and decouple the equations of motion by us-
ing the inverse dynamic model in the feedback loop.
State of the art hardware with high processing
power and low reaction times allows implementing
these methods, not only under laboratory conditions,
but also in industrial setups. With these tools at hand,
the suggested linearization strategies are used to con-
trol a St¨aubli RX130 industrial robot. Due to the fact
that the author is unaware of any works which com-
pare and investigate these approaches, this contribu-
tion tries to evaluate their performance. Focusing on
measurements, the occurring lag errors with different
control approaches are the basis for a final interpreta-
tion and conclusion.
2 SYSTEM DYNAMICS
In order to present detailed information on the multi-
body system under investigation,
Figure 1: Sketch of the RX130L.
Figure 1 shows a sketchofthe St¨aubli industrial robot.
It is a medium scale robot with six degrees of free-
dom, 1.6 m reach and a total mass of 235 kg.
Fundamentally, the basis for model based control
approaches are the equations of motion
M(q)
¨
q+ G(q,
˙
q)
˙
q+ Q(q,
˙
q) = Q
m
∈ R
n
, (1)
where q denotes the vector of minimal coordinates,
respectively the robots joint angles, M(q) is the con-
figuration dependent, positive definite and symmetric
mass matrix and G(q,
˙
q) contains the velocity depen-
dent nonlinearities as coriolis and centrifugal forces.
The vector Q(q,
˙
q) consists of all generalized forces,
192
Riepl R., Gattringer H. and Bremer H. (2010).
EVALUATION OF FEEDBACK AND FEEDFORWARD LINEARIZATION STRATEGIES FOR AN ARTICULATED ROBOT.
In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 192-197
DOI: 10.5220/0002918301920197
Copyright
c
SciTePress

e.g. forces resulting from gravity or friction. The ac-
tuating motor torques are separated on the right side
of the equations of motion and found in the vector
Q
m
. The variable n represents the number of degrees
of freedom which equals the number of joints, assum-
ing a rigid multi body system.
The equations of motion, as stated in (1), are com-
monly derived using analytical methods, e.g. with the
Lagrange equations. However, an articulated robot
consists of several joints and may be regarded as an
assembly of n arm/motor units.
Introducing such a unit, also called subsystem, as
sketched in Figure 2,
v
o
ω
F
q
Figure 2: An arm/motor subsystem.
with the vector
˙
y
k
˙
y
k
=
v
T
0
ω
T
F
q
T
k
(2)
containing the translational and rotational velocities
v
0
and ω
F
of the k-th subsystems reference frame and
the corresponding joint angle q, leads with the projec-
tion equation
N
sub
∑
k=1
∂
˙
y
k
∂
˙
q
T
[M
k
¨
y
k
+ G
k
˙
y
k
− Q
k
] = 0 (3)
in subsystem representation, see (Bremer, 2008), to
the equations of motion. This synthetical method,
based on projecting the linear and angular momen-
tum in the free directions of movement, effectively
makes use of the serial composition of several at-
tached arm/motor units. The interested reader may
find more information on the subsystems matrices and
vectors, M
k
, G
k
and Q
k
and their detailed derivation
in (Gattringer, 2006).
2.1 Model Verification
After an identification process as suggested in (Sciav-
icco and Siciliano, 2004; Khalil and Dombre, 2004),
the model parameters are verified by comparing mea-
sured and simulated motor torques. The simulation
is carried out by integrating the equations of mo-
tion. The reference trajectory for verification pur-
poses strictly differs from the ones used during the
identification process to assure the parameters’ cor-
rectness in the whole task space.
Figure 3 presents the accordance of the first three
joints. Joints four to six are of equivalent quality.
0 5 10 15 20 25
−5
0
5
Q
1
in Nm
Simulation Measurement
0 5 10 15 20 25
−10
−5
0
5
Q
2
in Nm
0 5 10 15 20 25
0
5
Q
3
in Nm
Time in s
Figure 3: Measured versus simulated motor torques.
3 MOTION CONTROL
This section summarizes the control strategies for
tracking the tool center point along a desired trajec-
tory. All introduced methods are part of the evaluation
process.
3.1 Decoupled PD-control
As the name suggests, the decoupled PD-control is
a decentralized single joint control law. Each single
axis compensates the nonlinearities, e.g. influences
from the other joints, while tracking the desired refer-
ence trajectory in joint space. The control law is given
by
Q
m
= K
P
(q
d
− q) + K
D
(
˙
q
d
−
˙
q), (4)
where the lower right index d denotes the desired ref-
erence values for joint positions and velocities. The
positive definite diagonal matrices K
P
and K
D
are the
proportional and derivative gains.
The major disadvantage of this common and sim-
ple control law is the lack of knowledge about the sys-
tem which is to be controlled.
Asymptotic stability can only be proven if the sys-
tem remains in steady state with the classical stabil-
ity theorems of mechanical systems, summarized in
(Bremer, 1988).
EVALUATION OF FEEDBACK AND FEEDFORWARD LINEARIZATION STRATEGIES FOR AN ARTICULATED
ROBOT
193

3.2 Decoupled PD-control with
Feedforward
To negate the major drawback of the decoupled PD-
control an additional feedforward term is inserted into
control law (4), yielding
Q
m
= K
P
(q
d
− q) + K
D
(
˙
q
d
−
˙
q) + u
FF
. (5)
Effectively exploiting the system knowledge, ob-
tained through the dynamic modeling and identifi-
cation, the necessary reference motor torques which
guide the tool center point along a desired trajectory,
are given with the equations of motion (1) and are so
intuitively suitable for a feedforward control
u
FF
= M(q
d
)
¨
q
d
+ G(q
d
,
˙
q
d
)
˙
q
d
+ Q(q
d
,
˙
q
d
). (6)
Obviously, if the reference trajectory is two times
continuously differentiable with respect to time, the
resulting feedforward torques will show a continu-
ous progression. This set of feedforward control is
also called exact feedforward linearization in litera-
ture, see (Hagenmeyer and Delaleau, 2003).
With this choice the PD-controller’s task is re-
duced to compensate modeling inaccuracies, param-
eter variations and external or unknown disturbances.
Proving asymptotic stability, however, still leads
to further challenges, because inserting the feedfor-
ward term and evaluating the equations of motion
transforms the dynamics to a nonlinear time-variant
system. The interested reader may find more infor-
mation in (Kugi, 2008; Hagenmeyer and Delaleau,
2003).
3.3 Computed Torque
Introducing the computed torque control law
Q
m
= M(q)
¨
v+ G(q,
˙
q)
˙
q+ Q(q,
˙
q) (7)
and inserting it into the equations of motion (1) yields
the system
¨
q = v (8)
of n double integrators, resulting in a solely linear in-
terrelation between the new system input v and the
joint angles q. A possible choice for the new system
input v is
v =
¨
q
d
+ K
D
(
˙
q
d
−
˙
q) + K
P
(q
d
− q) (9)
with the positive definite diagonal matrices K
P
and
K
D
as stabilizing gains.
By defining the joint tracking error e = q
d
−q and
inserting Equation (9) in (8) the system dynamics of
the tracking error e for the closed loop system
¨
q
d
−
¨
q+ K
D
(
˙
q
d
−
˙
q) + K
P
(q
d
− q) = 0
¨
e+ K
D
˙
e+ K
P
e = 0 (10)
is found. Equation (10) instantly allows to shape the
error dynamics by choosing the gains K
P
and K
D
, for
example by pole placement.
Please note, in literature the computed torque
method is also referred to as inverse dynamics,
feedback linearization or flatness based control, as
(Isidori, 1985; Slotine and Li, 1990; Fliess et al.,
1995) describe.
3.4 Extended Linearization
Similar to Subsection 3.3, the nonlinearities in the
equations of motion are eliminated with the control
law
Q
m
= M(q)(
¨
v+ K
0
q+ K
1
˙
q)
+ G(q,
˙
q)
˙
q+ Q(q,
˙
q). (11)
Inserting the control law (11) into the equations of
motion (1) yields
¨
q = v− K
0
q− K
1
˙
q (12)
or equivalent in state space representation
d
dt
q
˙
q
=
0 E
−K
0
−K
1
q
˙
q
+
0,
E
v,
(13)
which describes the dynamics of the closed loop sys-
tem. Apparently, this MIMO-system is controllable
with the whole repertory of tools available from linear
system theory, for example linear quadratic regulators
or pole placement, well summarized in (Chen, 1998).
Certainly, before designing a linear controller for
system (13), the matrices K
0
and K
1
need to be cho-
sen. It is suggested to pick them in a manner so
that the closed loop system (13) resembles its phys-
ical counterpart. One suggestion is that the eigenval-
ues of the linearized equations of motion may be used
as guideline for picking the eigenvalues of the closed
loop system. However, due to stability issues positive
eigenvalues in the closed loop system (13) need to be
avoided.
Asymptotic stability of Equation (13) is derived
with linear system theory.
3.5 Friction Feedback Issues
One common problem with feedback linearization
methods occurs when friction models are part of the
inverse dynamics. This is usually the case for any me-
chanical or robotic application. If the classical model
for friction
Q
fric
= d
v
˙q+ d
c
signum ( ˙q) (14)
is part of the feedback loop, then the noisy measure-
ment of the velocity signal ˙q will be amplified and fed
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
194

−1−2
2
−5
−10
0
0
5
10
1
Joint velocity ˙q
Friction Torque
Q
fric
Q
fric,b
Q
fric,a
Figure 4: Friction models for feedback loop.
through to the actuators, directly resulting in a dis-
turbing hum.
To counter this effect the friction characteristics
in the feedback loop have to be adapted. Two simple
solutions are given by
Q
fric,a
= d
v
˙q+ d
c
signum ( ˙q) for ˙q ≥ ε
1
Q
fric,a
= 0 else
or
Q
fric,b
= d
v
˙q+ d
c
tanh ( ˙q/ε
2
)
(15)
with suitable values for ε
1
and ε
2
. Figure 4 shows the
original and adapted friction models.
4 EXPERIMENTS
The introducedcontrol strategies are evaluated in a se-
ries of experiments. Additionally, details on the labo-
ratory setup and the recorded data are the dominating
topics of this section.
4.1 Setup
In the laboratory, the St¨aubli RX130 industrial robot
is interfaced with state-of-the-art motion hardware.
All mechanical and electrical parts of the robot itself,
like motors and resolvers, remain untouched. The
servo drives, powering the synchronous motors, and
the digital processing unit are of industrial standard
but still offer the necessary development tools for im-
plementing the proposed methods.
Figure 5 shows the main components and their in-
terrelation to each other. The central computing unit
is connected to six servo drives via a high-speed Pow-
erlink bus. Each servo drive acts as an amplifier for
the AC motor, evaluates resolver signals and may use
an internal linear cascaded controller for position and
velocity control of the attached motors.
Automation
PC
Servo
Drives
Robot Mechanics
Figure 5: Setup.
4.2 Trajectory
A reference trajectory with significant characteristics
is necessary for the process of evaluation. It needs to
cover a reasonable workspace while containing high
dynamics, even in disadvantageous poses and config-
urations.
A suitable choice, meeting this prerequisites, is
found in (ISO NORM 9283, 1998) which originally
defines a standardized trajectory for tool center point
measurements and evaluations. By sharing a common
objective, the proposed trajectory is also the reference
in the following experiments.
The velocity and acceleration of the tool center
point is given with 1 m/s and 5 m/s
2
. These set-
tings represent the highest values without exceeding
the available actuating torques. The trajectory itself is
a composition of straight lines, circles and squares in
space.
The inverse kinematics is computed numerically,
yielding the according joint values and their deriva-
tives with respect to time. It is also guaranteed that
all reference joint angles are two times continuously
differentiable with respect to time.
4.3 Centralized / Decentralized Control
When realizing the introduced control structures on
the industrial hardware, the feedforward and feed-
back approach show major differences. Basically, the
model based control methods – feedforward as well
as feedback – evaluate the equations of motion each
sample step in order to linearize the mechanical sys-
tem. Furthermore some stabilizing gains guarantee
stability.
However, in the case of feedforward control,
which is a decoupled and decentralized method, the
stabilizing PD feedback loop may be implemented di-
rectly on the servo drives which profit from very short
response times and a fast sampling rate. On the other
hand, linearizing the system only by using reference
values instead of actual ones, is not as exact as with
feedback linearization.
EVALUATION OF FEEDBACK AND FEEDFORWARD LINEARIZATION STRATEGIES FOR AN ARTICULATED
ROBOT
195
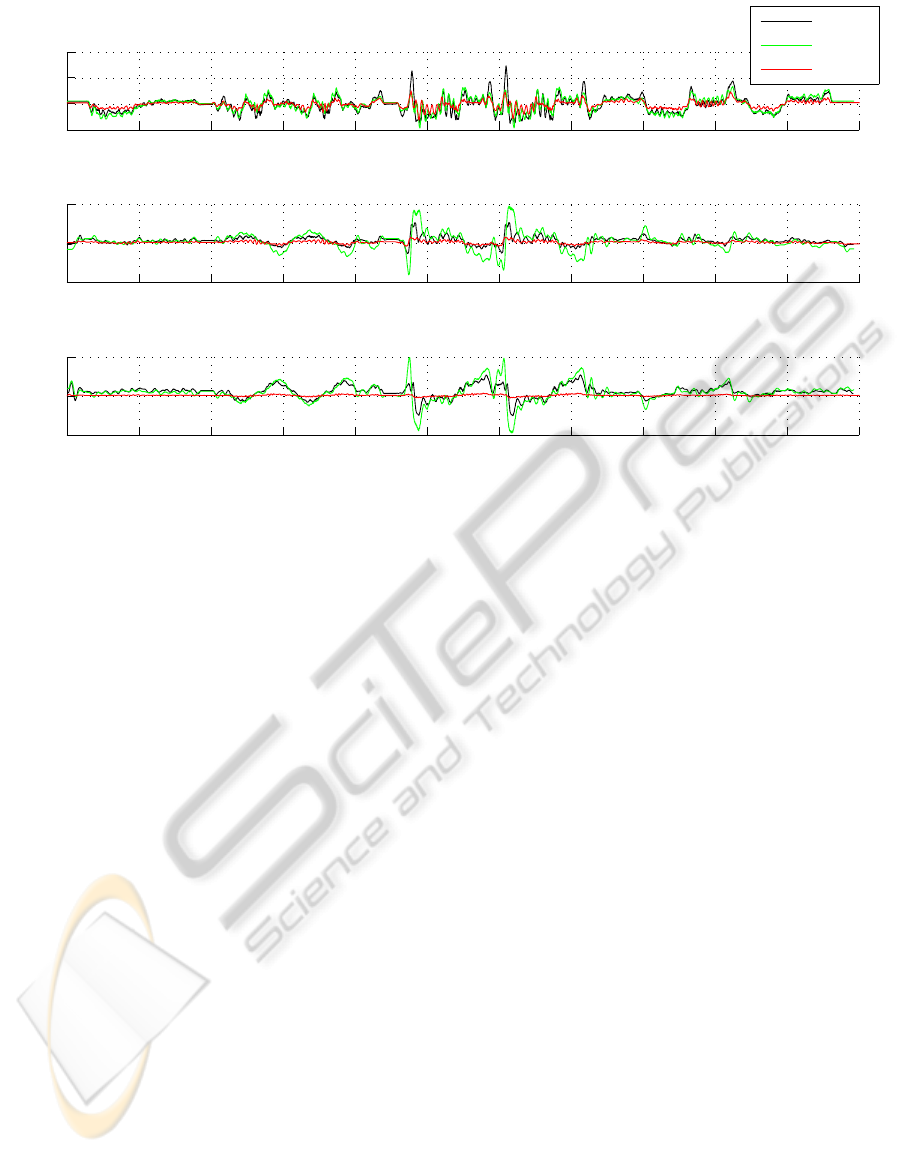
x 10
x 10
0
0
0
0
0
0
2
2
2
2
4
4
4
6
6
6
8
8
8
12
12
12
14
14
14
16
16
16
18
18
18
20
20
20
22
22
22
−5
5
−1
1
10
10
10
−3
−3
0.01
−0.01
e
1
in rad
e
2
in rad
e
3
in rad
time t in s
time t in s
time t in s
e
Lin
e
CT
e
FF
Figure 6: Lag errors with various control strategies.
4.4 Results
During a series of experiments the lag errors of the
joints are recorded. Due to the rigid construction and
the high stiffness of the gears, the joints’ lag errors
may be used to give estimations for the tool center ac-
curacy. Also, all design parameters are chosen with
highest possible gains which were evaluated in an-
other set of preceding investigations.
In Figure 6, the lag errors for joint one, two and
three are revealed. The lag errors resulting with ex-
tended linearization are denoted with e
Lin
, respec-
tively the ones with computed torque and feedforward
with e
CT
and e
FF
.
While the performance of the control methods
seems to be nearly equal for joint one, the joints
two and three show different results. Especially axes
with high loads resulting from gravity are benefiting
from their reduced lag errors with the feedforward ap-
proach.
The axes four, five and six are of similar behav-
ior and thus omitted. All values presented are joint
angles, transformed to the gears’ output sides.
5 INTERPRETATION
It is clearly not immediately evident that the feedfor-
ward linearization excels in performance in case of
this robotic application. The reason lies in the struc-
ture of control. If the feedforward linearization
is used in combination with the decoupled PD - con-
trol, the servo drives assume the task of decentralized
controllers. These decentralized controllers profit
from very short cycle times, still supported by the
feedforward variables.
The centralized control methods, which linearize
the system by feedback, are mathematically outstand-
ing and superior. However, due to the delays which
arise from closing the feedback loop to the central
processing unit, the maximum gains are drastically re-
duced. Thus, deviations from the model and external
disturbances are eliminated in a slower manner.
The effort for preparation – originating from ob-
taining the dynamic model with a valid and well iden-
tified set of parameters – is equal for all proposed
model-based control strategies because they share a
common origin, the equations of motion.
To sum up, the method of choice to control the
motion of an articulated robot with six axes is the
feedforwardlinearization approach. Model based sys-
tem knowledge can effectivelybe exploited to support
the servo drives internal, fast sampling controllers
which are technically mature and professional prod-
ucts.
6 CONCLUSIONS
With the interpretation at hand, the feed forward lin-
earization technique is investigated in more detail.
From a practical viewpoint, the endeffector error
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
196

along a given trajectory is a characteristic of interest.
Assuming a rigid model and high gear stiffnesses, the
forward kinematics is evaluated to compute the de-
viation between the desired trajectory and the actual
trajectory.
To analyze the effects of the feedforward lin-
earization, the experiment is conducted with and
without superimposed feed forward loop. Figure 7
shows the tool center point (short TCP) error in iner-
tial coordinates. The x- and y-axes are parallel to the
robots mounting surface whereas the z-axis points in
the same direction as the gravity vector.
0 5 10 15 20
−5
0
5
10
x 10
−3
TCP error in m
without feed−forward
0 5 10 15 20
−5
0
5
10
x 10
−3
Time in s
TCP error in m
with feed−forward
e
x
e
y
e
z
Figure 7: Evolution of TCP errors.
Interpreting the plot shows, that the robots manip-
ulator has nearly an average of 4 mm deviation in di-
rection of the z-axis. This static payload of the robot’s
own mass is instantly compensated with the feed for-
ward approach. During the phases with high dynam-
ics, the result with feed-forward control is also con-
siderably improved.
ACKNOWLEDGEMENTS
The authors acknowledge the support and coopera-
tion with Bernecker & Rainer, especially the group
of Alois Holzleitner and Gernot Bachler. The motion
control system provided allows quick implementation
and offers technical perfection which made this re-
search possible.
REFERENCES
Bremer, H. (1988). Dynamik und Regelung mechanischer
Systeme. Teubner Studienb¨ucher, Stuttgart.
Bremer, H. (2008). Elastic Multibody Dynamics: A Di-
rect Ritz Approach, volume 35 of Intelligent Systems,
Control, and Automation: Science and Engineering.
Springer-Verlag GmbH.
Chen, C.-T. (1998). Linear System Theory and Design (Ox-
ford Series in Electrical and Computer Engineering).
Oxford University Press, third. edition.
Fliess, M., L´evine, J., and Rouchon, P. (1995). Flatness and
defect of nonlinear systems: Introductory theory and
examples. International Journal of Control, 61:1327–
1361.
Gattringer, H. (2006). Realisierung, Modellbildung und
Regelung einer zweibeinigen Laufmaschine. PhD the-
sis, Johannes Kepler Universit¨at Linz.
Hagenmeyer, V. and Delaleau, E. (2003). Robustness anal-
ysis of exact feedforward linearization based on dif-
ferential flatness. Automatica, 39(11):1941 – 1946.
Isidori, A. (1985). Nonlinear Control Systems. Springer-
Verlag.
ISO NORM 9283 (1998). Manipulating industrial robots -
performance and criteria. Norm, EN ISO 9283.
Khalil, W. and Dombre, E. (2004). Modeling, Identification
and Control of Robots. Kogan Page Science, London.
Kugi, A. (2008). Introduction to tracking control of finite-
and infinite-dimensional systems. Stability. Identifi-
cation and Control in Nonlinear Structural Dynamics
(SICON).
Sciavicco, L. and Siciliano, B. (2004). Modelling and Con-
trol of Robot Manipulators. Springer, United King-
dom.
Slotine, J.-J. and Li, W. (1990). Applied Nonlinear Control.
Prentice Hall.
EVALUATION OF FEEDBACK AND FEEDFORWARD LINEARIZATION STRATEGIES FOR AN ARTICULATED
ROBOT
197
