
DEFORMABLE IMAGE REGISTRATION
Improved Fast Free Form Deformation
Bartłomiej W. Papież, Tomasz P. Zieliński
Department of Telecommunications, AGH University of Science and Technology, Krakow, Poland
Bogdan J. Matuszewski
ADSIP Research Centre, University of Central Lancashire, Preston, U.K.
Keywords: Medical image registration, Free-form deformation, Numerical methods, Prostate cancer.
Abstract: In this paper, we describe a class of deformable registration techniques with application to radiotherapy of
prostate cancer. To solve registration problem we introduced Jacobi and successive over-relaxation methods
and compared them with the Gauss-Seidel used in the variational framework previously proposed in
literature. A multi-resolution scheme was used to improve speed of computation, robustness and ability to
recover bigger image deformations. To investigate the properties of these algorithms they were tested using
simulated data with known displacement filed and real CT images . The results show that it is possible to
improve currently widely used algorithms by introducing simple modifications in the numerical solving
scheme.
1 INTRODUCTION
Prostate cancer is a common cause of cancer death
among men in the world. In Poland in 2006 there
were more than 7 thousand new cases estimated,
whereas in the United Kingdom more than 35
thousand with respectively 3.5 and 10 thousand
deaths due to prostate cancer. The accurate and fast
tools for diagnosis, surgical planning and treatment
are required. The image registration and
segmentation are the fundamental tools, which are
instrumental in achieving effective image-guided
radiation therapy.
The image registration can be described as a
process of finding optimal geometric transformation
between images which have similar contents in some
sense. The images can be taken from different
scanners, at different time and from different
positions. Moreover, in medical imaging there is no
guarantee that there is one-to-one correspondence
between images (e.g. due to missing data).
The image registration methods can be broadly
divided into two main categories, feature-based and
intensity-based methods. The feature-based
registration methods require a pre-processing step to
extract corresponding image features such as points,
lines and curves. By matching the corresponding
image features, deformation of the whole image can
be calculated using one of “smooth” interpolation
methods (Little et al (1997, Rohr et al (2001)). The
intensity-based methods operate directly on image
intensity values. One of the most popular methods is
to calculate the transformation using a set of equally
spaced sparse control points, which are not linked to
any specific image features, by finding the optimum
of the cost function defined in the neighbourhood of
the control points. The image deformations are
calculated from displacement of sparse control
points using one of interpolation methods mentioned
above (MacCraken et al (1996)). As the number of
control points might be significant, additional
regularisation measures are necessary to avoid
excessive variation of the deformation field.
Rueckert et al (1999) applied the global affine
transformation first, and subsequently used the B-
spline interpolation and a penalty function which is a
3D counterpart of the 2D bending energy of the
Thin-Plate Spline. Schnabel et al (2001) extended
and generalised the work described in (Rueckert et
al (1999)) by introducing multi-resolution
optimisation and allowing non-uniform distribution
of control points. (Matuszewski et al (2003), Shen et
530
W. Papie
˙
z B., P. Zieli
´
nski T. and J. Matuszewski B. (2010).
DEFORMABLE IMAGE REGISTRATION - Improved Fast Free Form Deformation.
In Proceedings of the International Conference on Computer Vision Theory and Applications, pages 530-535
DOI: 10.5220/0002920105300535
Copyright
c
SciTePress

al (2005), Shen et al (2006)) proposed further
extension by describing interaction between control
points using physical analogies.
Another often used intensity-based method is to
model the displacement field by using physical
analogies. The first such methods were schemes
using the Navier-Lamé Partial Differential Equations
(PDEs) to model elastic behaviour of the registered
data (Bajcy and Kovacic (1989)), and scheme using
the Navier-Stokes PDEs to model fluid deformations
(Christensen et al (1996)). The systematic overview
of these methods can be found in (Modersitzki
(2004))
This paper describes modifications in the
numerical solving scheme of a previously proposed
method (Lu et al (2004)) based on variational
formulation of the registration problem. It is shown
that relatively simple modifications improve the
performance of the original method.
The remainder of this paper is organized as
follows: Section 2 describes shortly method of
image registration used in this paper: registration
using variational formulation, method of solving
resulting partial differential equations system (PDE)
and similarity measure which was used for
comparison. Section 3 describes and visualizes
results of our experiment on simulated data and on
real CT images. In section 4 we draw conclusions of
those tests.
2 THEORY
In this section methods of image registration used
for test are shortly described.
2.1 Deformable Registration
In general, deformable registration is problem of
minimization distance between reference image
A(x) and moving image B(x) with respect to
deformation u.
min
,
(1)
A minimization of distance measure is the ill-posed
problem (e.g. the solution can be not unique). To
solve this problem we add additional term S. There
is no general way of choosing regularizing term and
there is many different approaches provided depend
on desired final results.
min
,
(2)
2.1.1 Free-form Deformation
W. Lu described the free-form deformable
registration as process of computing a displacement
which minimizes energy of functional :
argmin
(3)
where
,
(4)
Here
,
is residual,
is reference image,
is moving image and
. To find displacement field u, the calculus
of variations is used and the problem of deformable
registration becomes the problem of solving the non-
linear elliptic partial differential equations.
R
,
∂R
,
∂
0
(5)
To solve an equation (5) a finite difference scheme
previously proposed in literature is used. After
discretizing equation (5), we have:
,
,
g
,
(6)
Where m=1,…,N (N denoting the total number of
volume voxels) is a voxel index using
lexicographical ordering; n=1,2,3 is an index
corresponding x, y, and z dimensions,
;
; g
,
g
with
g
;
The displacement field is estimated using one step of
Newton iterations:
,
,
,
,
(7)
2.2 Criterion of Registration Quality
To assess the quality of registration in tested data we
calculated the correlation coefficient (CC).
∑
∑
∑
(8)
Here
and
are the mean intensity of
the reference and moving image. Better registration
means than value of CC is closer 1.
For simulated data the sum of squared
differences (SSD) is calculated between known
DEFORMABLE IMAGE REGISTRATION - Improved Fast Free Form Deformation
531

deformation field u(x) deformation field and
estimated field :
1
(9)
For perfect registration the value of SSD is 0.
2.3 Solution Scheme
To solve system of nonlinear elliptic partial
differential equation, the finite difference scheme
was used. After that we can use iterative method to
compute u. Update scheme for each iteration is as
follows:
• Calculate
using central difference
scheme
• Interpolate using tri-linear interpolation
and gradient
• Calculate according to equation (6)
• Update deformation field using
equation (7)
Previously in literature Gauss-Seidel scheme was
proposed to calculate and . In this paper Jacobi
and SOR scheme is introduced to calculate and .
2.3.1 Jacobi Method
The Jacobi method solves element
using
previously computed value
for each iteration.
This may be written as:
∑
(10)
2.3.2 Gauss-Seidel method
The Gauss-Seidel method solves element
using
already computed values of
and previously
computed value
. This may be written as:
∑
∑
(11)
2.3.3 Successive Over-relaxation Method
If we make an overcorrection to
at the k-th
iteration of Gauss-Seidel method by introducing
over-relaxation parameter ω we get method called
successive over-relaxation (SOR). This may be
written as:
1
∑
)
(12)
There is many various automated method for
choosing parameter ω but there are no general rules.
3 EVALUATION AND RESULTS
Evaluation of registration quality is done in two
ways. At the first stage, we prepared simulated data
with generated ground truth displacement field and
then we used previously described algorithms to
estimated this displacement field. At the second
stage we used real CT data from radiotherapy of
prostate cancer.
Free-form deformable registration with each
scheme was implemented in Matlab. All three
methods are implemented in the multiresolution
manner to reduce the computation time, improve
accuracy by avoiding local extremes and improve
ability to recover large displacement.
3.1 Simulated Data
Simulated data used in our tests are shown on Figure
1. First image is the reference image, second image
is the warped version of the first image by applying
the known displacement field. Figure 2 visualizes
deformation field introduced into reference image,
arrows shows the direction of displacement from
reference image to moving image. The arrows are
calculated as gradient of function used to deform
image. For those experiments, the objective is to
recover known deformation field using three
previously described methods.
Figure 1: Simulated reference and moving image.
Figure 2: Simulated deformation field introduced into
reference image.
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
532
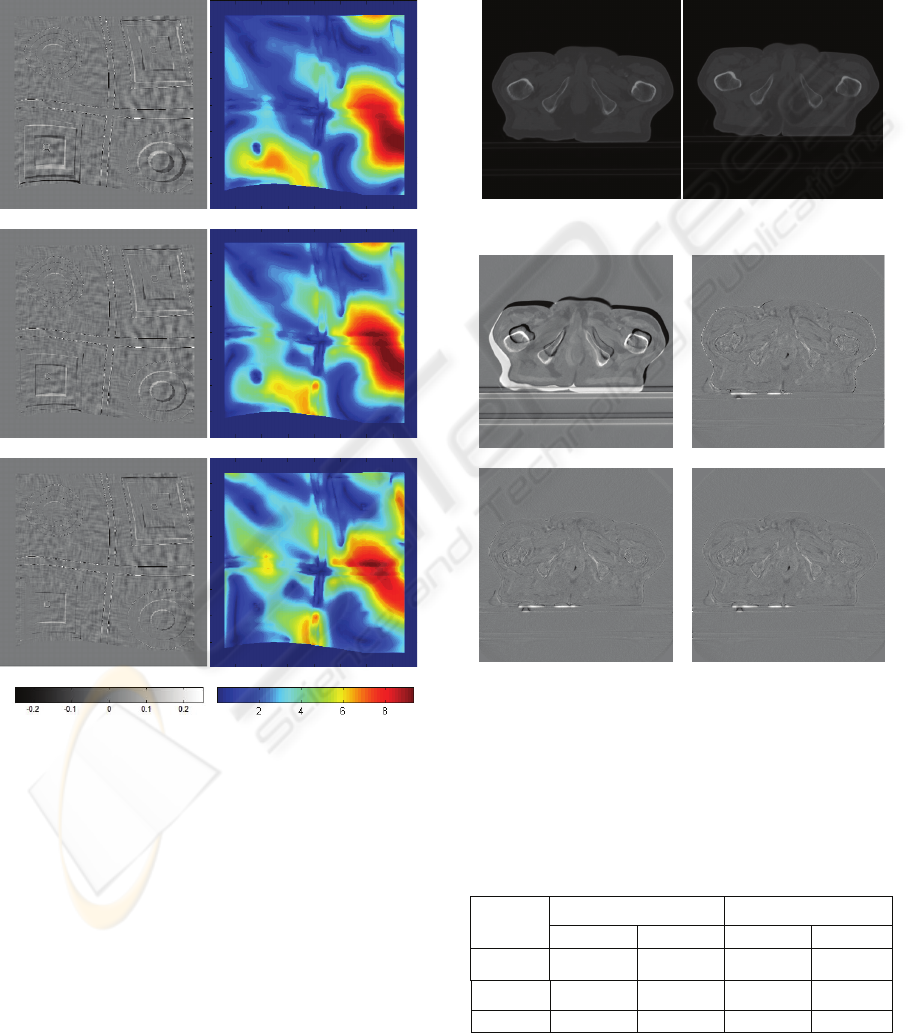
Figure 3 shows image differences between reference
image and moving image and the error magnitude
between known and estimated deformation after
registration. For the same number of iteration the
FFD method using SOR scheme achieved slightly
better results than Gauss-Seidel and Jacobi scheme.
It is due to the fact that SOR and Gauss-Seidel
scheme provide faster convergence.
(a) (b)
(c) (d)
(e) (f)
Figure 3: Image difference between references image and
moving image after registration and error magnitude
between known and estimated deformation field for Jacobi
method (a)-(b), Gauss-Seidel method (c)-(d) and SOR
method (e)-(f) .
3.2 Real CT Data
The evaluation of registration methods was done on
real medical data from radiotherapy of prostate
cancer. For each patient, we had got two CT data
sets, first from radiotherapy planning used as
reference image and second taken during treatment
process used as moving image. We provide tests for
2D images (taken as slice form 3D data set) and for
3D data. Figure 4 shows slices from CT images. The
quality of registration was measured for the same
number of iterations for each method in two ways:
first as value of correlation coefficient and the
second as image differences between images. The
relaxation parameter and weight of Laplacian were
selected empirically.
Figure 4: CT images: reference and moving image.
(a) (b)
(c) (d)
Figure 5: Image differences: (a) between reference image
and moving image before registration, and after
registration using Jacobi scheme (b), Gauss-Seidel scheme
(c) and SOR scheme (d).
Table 1: Intensity CC and values of SSD calculated for
corresponding displacement fields after 2D registration
using tested methods. (the same number if iterations was
applied to each method).
After 20 iterations After 80 iterations
CC SSD CC SSD
Jacobi 0,9979 25,55 0,9985 9,91
G-S 0,9983 16,34 0,9987 7,73
SOR 0,9986 9,49 0,9988 6,17
DEFORMABLE IMAGE REGISTRATION - Improved Fast Free Form Deformation
533

Figure 5 visualises results images after
registration using different scheme for fast free-form
registration.
Figure 6: 3D reference and moving image used in tests and
image difference between them.
Figure 6 shows reference image taken from planning
and moving image taken from treatment process and
difference between them.
Figure 7 shows difference after registration. All
methods were able to recover large displacement of
patient and for each the similarity measures was
significantly improved. Figure 8 shows value of CC
for different number of executed iterations for each
method. SOR scheme is dependent on value of
relaxation parameter. In some cases we can achieve
better accuracy of registration using Gauss-Seidel
scheme than SOR with non-optimal relaxation
parameter. For Jacobi scheme it is necessary to
calculate more iterations to achieve the similar
accuracy of registration.
Figure 7: Image difference between (from left to right)
Jacobi, Gauss-Seidel and SOR scheme.
Figure 8: Correlation coefficient for each method after the
same number of executed iterations.
4 CONCLUSIONS
The paper has been focused on evaluation of
currently known methods of registration. We show
that it is possible to achieve better quality of
registration for these methods by introducing simply
numerical improvements.
VISAPP 2010 - International Conference on Computer Vision Theory and Applications
534

For simulated data we have achieved slightly
better results using SOR scheme, this is due to fact
that SOR scheme get convergence faster than Gauss-
Seidel and Jacobi scheme. Each method is able to
recover large deformation field introduced into
moving image.
For CT data, all methods achieve similar results.
The main differences between tested methods were
the number of executed iterations to achieve similar
value of correlation coefficient and the sum of
squared differences. In every case the Jacobi method
required twice the number of iteration compared to
Gauss-Seidel. It is due fact that Gauss-Seidel and
SOR scheme has faster convergence.
The main difficulty with SOR scheme is an
optimal selection of the over-relaxation parameter.
The optimal value of this parameter is data
dependent. In our experiments this values was
chosen empirically. In some cases, using non-
optimal values of over-relaxation parameter provides
smaller accuracy and quality of registration than
Gauss-Seidel scheme.
In general the quality of registration depends on
data and there is no possibility to show the most
accurate method. Fast Free-Form Deformation
algorithm is suitable to recover large displacement.
Also it is possible to use this algorithm during the
radiotherapy of prostate cancer because of short
computation time of deformation field.
ACKNOWLEDGEMENTS
The work presented in this paper has been supported
from the MEGURATH project (EPSRC project No.
EP/D077540/1). The authors would like to thank Dr
Paweł Kukołowicz from the Holy Cross Hospital for
supplying CT images.
REFERENCES
W. Lu, M. L. Chen, G. H. Olivera, K. J. Ruchala, T. R.
Mackie, 2004, Fast free-form deformable registration
via calculus of variations. In Physics in Medicine and
Biology, 49:3067-3087
B. J. Matuszewski, J.-K. Shen and L.-K. Shark, 2003,
Elastic Image Matching with Embedded Rigid
Structures Using Spring-Mass System. In Proceedings
of IEEE International Conference on Image
Processing, ICIP-2003. Vol. 10, pp.937-940
J. Modersitzki, 2004, Numerical Methods for Image
Registration, Oxford University Press,
D. Rueckert, L. I. Sonoda, C. Hayes, D. L. G. Hill, M. O.
Leach, D. J. Hawkes, 1999, Nonrigid Registration
Using Free-Form Deformation: Applications to Breast
MR Images. In IEEE Transactions on Medical
Imaging. Vol. 18 No.8. pp. 712-721
J.-K. Shen, B.J. Matuszewski and L.-K. Shark, 2003,
Deformable Image Registration. In Proceedings of
IEEE International Conference on Image Processing,
ICIP’2005. Vol. 3, pp. 1112-1115.
J.-K. Shen, B.J. Matuszewski, L.-K. Shark and C.J.
Moore, 2006, Deformable image registration using
spring mass system. In British Machine Vision
Conference, BMVC06, Vol. 3, pp 1199-1208.
J.-P. Thirion, 1998, Image matching as a diffusion
process: an analogy with Maxwell’s demons. In
Medical Image Analysis, Vol. 2, No. 3, pp-243-260
W. H. Press, S. A. Teukolsky, W. T. Vetterling, B. P.
Flannery, 1992. Numerical recipes in C:The art of
scientific computing, Cambridge University Press
T. S. Yoo, 2004. Insight Into Images. Principles and
Practice for Segmentation, Registration and Image
Analyses. National Library of Medicine.
J. A. Little, D.L.G. Hill and D.J. Hawkes, 1997.
Deformations Incorporating Rigid Structures. In
Computer Vision and Image Understanding. Vol. 66,
No. 2, pp. 223-232.
K. Rohr, H.S. Stiehl, R. Sprengel and et al., 2001.
“Landmark-based elastic registration using
approximating thin-plate spline”. In IEEE
Transactions on Medical Imaging, Vol. 20, pp. 526-
534.
R. MacCraken, K. Joy, 1996. Free-form deformations with
lattices of arbitrary topology. In Computer Graphics
Proceedings, Annual Conference Series, Proceedings
of SIGGRAPH 96. pp 181-188. ACM SIGGRAPH.
J. A. Schnabel, D. Rueckert and et al., 2001. A Generic
Framework for Non-rigid Registration Based on Non-
uniform Multi-level Free-Form Deformations. In Proc.
MICCAI 2001, Lecture Notes in Computer Science.
Vol.2208, pp.512-721.
R. Bajcsy and S. Kovacic, 1989. Multiresolution elastic
matching. In Computer Vision, Graphics and Image
Processing. Vol. 46, pp. 1-21.
G. E. Christensen, R.D. Rabbitt and M.I. Miller, 1996.
Deformable Templates Using Large Deformation
Kinematics. In IEEE Transactions on Image
Processing. Vol. 5, pp. 1435-1447.
DEFORMABLE IMAGE REGISTRATION - Improved Fast Free Form Deformation
535
