
EXPERIMENTS WITH A CONTINUUM ROBOT STRUCTURE
Dorian Cojocaru, Sorin Dumitru, Florin Manta, Giuseppe Boccolato
Faculty of Automation, Computers and Electronic, University of Craiova, Bld. Decebal, Craiova, Romania
Ion Manea
Faculty of Mechanics, University of Craiova, Calea Bucuresti Str., Craiova, Romania
Keywords: Continuum Robots, Kinematics, Mechanical Experiments.
Abstract: A continuum arm prototype was designed and implemented using two different shapes: cylinder like and
cone like. This new robot is actuated by stepper motors. The rotation of these motors rotates the cables
which by correlated screwing and unscrewing of their ends determine their shortening or prolonging, and by
consequence, the tentacle curvature. The kinematics and dynamics models, as well as the different control
methods developed by the research group were tested on these robots. The lack of no discrete joints is a
serious and difficult issue in the determination of the robot’s shape. A solution for this problem is the vision
based control of the robot, kinematics and dynamics. An image – based visual servo control where the error
control signal is defined directly in terms of image feature parameters was designed and implemented. In
this paper, we analyze some mechanical capabilities of this type of continuous robots. We present the
structure of the tentacle robot, it’s kinematics model and the results for a series of tests regarding the
mechanical behaviour of the robotic structure.
1 INTRODUCTION
Modern industrial robots are mostly (human) arm-
inspired mechanisms with serially arranged discrete
links. When it comes to industrial environment
where the workspace is structured and predefined
this kind of structure is fine. This type of robots are
placed in carefully controlled environments and kept
away from human and their world.
When it comes to robots that must interact with
the natural world, it needs to be able to solve the
same problems that animals do. The rigid structure
of traditional robots limit their ability to maneuver
and in small spaces and congested environments,
and to adapt to variations in their environmental
contact conditions (Suzumori et al., 1991),
(Robinson and Davies, 1999). For improving the
adaptability and versatility of robots, recently there
has been interest and research in “soft” robots
(Cowan and Walker, 2008). In particular, several
research groups are investigating robots based on
continuous body “continuum” structure. If a robot’s
body is soft and/or continuously bendable it might
emulate a snake or an eel with an undulating
locomotion (Crespi and Ijspeert, 2006).
The continuum or hyper-redundant robot
manipulators behaviour is similar to biological
trunks, tentacles or snakes. The movement of the
continuum robot mechanisms is generated by ending
continuously along their length to produce a
sequence of smooth curves (Blessing and Walker,
2004). This contrasts with discrete robot devices,
which generate movement at independent joints
separated by supporting links.
We can also describe as continuum robots snake-
like robots and elephant’s trunk robots, although
these descriptions are restrictive in their definitions
and cannot be applied to all snake-arm robots. A
continuum robot is a continuously curving
manipulator, much like the arm of an octopus
(Davies, J.B.C., 1998). An elephant’s trunk robot is
a good descriptor of a continuum robot. The
elephant’s trunk robot has been generally associated
with an arm manipulation – an entire arm used to
grasp and manipulate objects, the same way that an
elephant would pick up an apple. Snake-arm robots
are often used in association with another device
meant to introduce the snake-arm into the confined
space. However, the development of high-
198
Cojocaru D., Dumitru S., Manta F., Boccolato G. and Manea I. (2010).
EXPERIMENTS WITH A CONTINUUM ROBOT STRUCTURE.
In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 198-205
DOI: 10.5220/0002921501980205
Copyright
c
SciTePress

performance control algorithms for these
manipulators is quite a challenge, due to their unique
design and the high degree of uncertainty in their
dynamic models. The great number of parameters,
theoretically an infinite one, makes very difficult the
use of classical control and the conventional
transducers for position and orientation.
2 THE ROBOTIC STRUCTURE
A research group from the Faculty of Automation,
Computers and Electronics, University of Craiova,
Romania, started working in research field of hyper
redundant robots over 20 years ago. The
experiments started on a family of TEROB robots
which used cables and DC motors. The kinematics
and dynamics models, as well as the different
control methods developed by the research group
were tested on these robots. Since 2008, the research
group designed a new experimental platform for
hyper redundant robots.
Our robotic system is composed from two units,
one with a flexible structure with kinematic
possibilities similar with the snake’s locomotion and
another one with driving. The flexible unit is
composed from three modules with independent
driving, that confers a complex 3D configuration,
with multiple kinematic possibilities for the working
space. The flexible structure is conceived in modular
systems with decoupling possibilities for a
controlled optimization of the working space.
The flexible structure as an integrate system, or
as independent modules, is conceived to allow
driving in two modes, respective:
- one with wires and a flexible central column;
- one with flexible vertebrates and a flexible
central column;
In the case where the driving is made by wires, a
module has two freedom degrees and in the case of
driving with flexible columns each module has three
degrees of freedom. As it can be observed the
flexible unit structured in three modules for
controlling a complex workspace, with multiple
kinematic possibilities. The machine structure for
each module is based upon thread transmissions with
self decelerations possibilities and adjust of the
axial-radial clearances.The flexible unit with the
snake-like design is composed from a base flange,
some intermediary flanges, and four flexible shafts,
with high elasticity, which will be called vertebral
spines. The central shaft is mounted rigidly to all the
intermediary flanges, fig. 1.
The three super elastic spines are mounted
equidistantly upon the central spine. The entire
vertebrates are connected only to the end flange. The
intermediary flanges maintain constant the radial
distance between the secondary tubes and the central
vertebrate. Changing in an active way the length for
two of the vertebrate spines, the final flange can be
manipulated with two degrees of freedom in any
direction.
The three actuating spines are rigidly jointed
only to the end flange, the joint between them and
the intermediary flanges is like one translational
joint.
Figure 1: The virtual model with the driving and vertebral
unit.
Figure 2: Redundant driving unit.
Figure 3: The assembly of the robotic system with the
baggy vertebral unit.
EXPERIMENTS WITH A CONTINUUM ROBOT STRUCTURE
199
2.1 Experimental Modelling
As it was presented above, the robot is designed in a
modular structure, with three modules,
independently actuated through thread transmissions
with possibility to adjust the radial and axial
clearances, in the aim to assure the imposed
kinematics precision. The vertebrate unit is designed
to work in two ways, respectively with two or three
degrees of freedom on each module.
2.2 Modelling with Finite Elements
For demonstrating the viability of mechanical
system it is proposed the modelling and simulation
functionality with finite element method. Faithfully
are respected the shape conditions and loadings, so
that through a Virtual Prototyping attempt it is
obtained a parameterized virtual system, which can
be loaded so that you get various types of deformed
shapes, obviously controlled for the analyzed
mechanic system (Dumitru et al., 2009).
Parameterized modelling of the flexible system
allows 3D simulation for different variants with one,
two or three modules, with different size dimensions
and types of materials with circular vertebras full or
tubular, in this way assuring a wider area of skills
for the proposed and analyzed system.
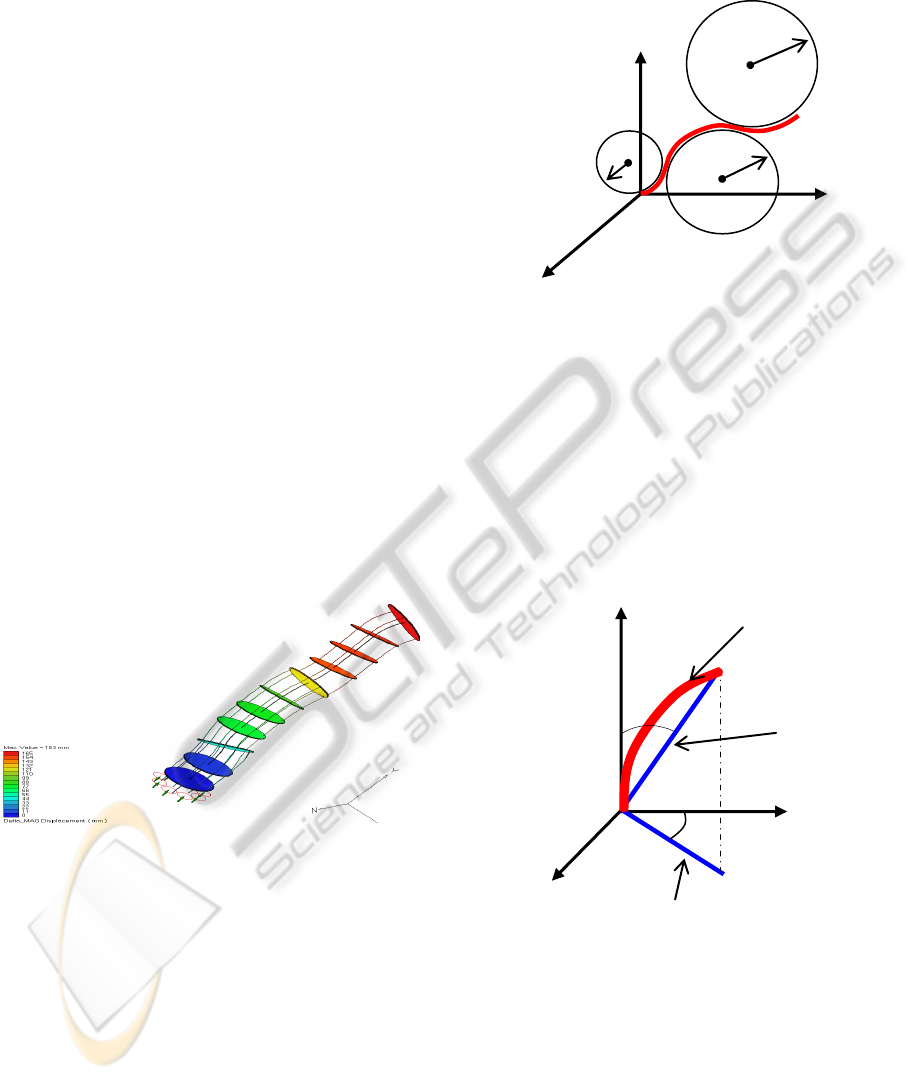
Figure 4: Elastic displacement distribution for a kinematic
chain with 3 modules.
3 THE KINEMATIC MODEL OF
THE TENTACLE ARM
In order to control a hyper-redundant robot we have
to develop a method to compute the positions for
each one of his segments (Ivanescu et al., 2006). By
consequence, given a desired curvature S*(x, tf) as
sequence of semi circles, identify how to move the
structure, to obtain s(x, t) such that:
),(),(lim
*
ftt
txStxs
f
=
→
(1)
where x is the column vector of the shape
description and tf is the final time (see Fig. 6).
Y
X
R
R
2
R
1
Z
Figure 5: The description of the desired shape.
3.1 Tentacle Shape Description
The tentacle’s shape will be described considering
two angles (θ, α) for each segment, where θ is the
rotation angle around Z-axis and is the rotation angle
around the Y-axis (see Figure 5). In order to
describe the movement we can use the roto-
translation matrix as shown in Figure 6. Figure 7
shows the relation between the orientation of one
projection on the main plane segment and the
curvature angle of the previous segment.
X
Y
Z
segment
chord
projectiononthemainplane
θ
α
Figure 6: The description of a 3D curvature.
(
)
(
)
() ()
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
⋅
⋅⋅
⋅
⋅⋅
−
100
)cos(L
2
cos
2
sin
)sin(L
2
sin
2
cos
β
ββ
β
ββ
(2)
The generic matrix in 2D that expresses the
coordinate of the next segment related to the
previous reference system can be
written as follow:
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
200
centre
originalpositionofthe
segment
L
θ
β
2β
Figure 7: Curvature and relation between θ
and β.
In 3D space we cannot write immediately the
dependence that exists between segments. This
relation can be obtained through the pre-
multiplication of generic roto-translation matrix
(Cojocaru et al., 2008). One of the possible
combinations to express the coordinate of the next
segment related to the frame coordinate of the
previous segment is the following:
:()()()()
iiiiiiii
generic z y y z
RRTrVRR
θ
αθ
=⋅ ⋅⋅
(3)
where
)(R
ii
z
θ
and
)(R
ii
y
α
are the fundamental
roto-translation matrix having 4x4 elements in 3-D
space, and Try(V) is a 4x4 elements matrix of pure
translation in 3-D space and where Vi is the vector
describing the translation between two segments
expressed in coordinate of i-th reference system. The
main problem remains to obtain an imposed shape
for the tentacle arm. In order to control the robot, we
need to obtain the relation between the position of
the wires and the position of the segment.
3.2 Curvature of One Segment
In the current stage of our research, a decoupled
approach is used for the robot control scheme, thus
the three segments are
controlled separately, without
considering the interaction between them. This
section presents the way direct kinematics of one
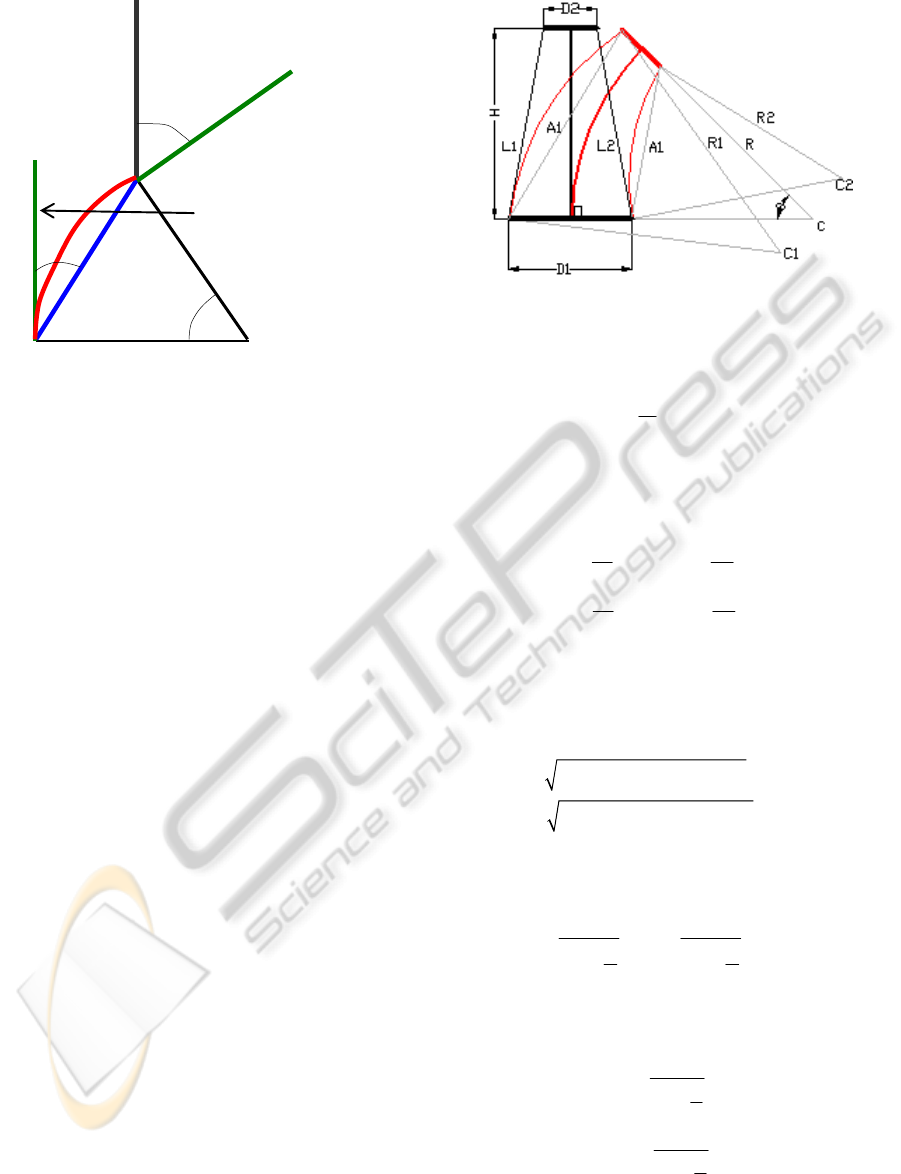
segment was obtained. The geometry of one
segment for the 2D case is described in Fig. 10. The
curvature angle θ of the segment is considered as the
input parameter, while the lengths L1 and L2 of the
control wires are the outputs (Boccolato et all.,
2009).
Figure 8: The geometry of one segment.
The radius R of the segment curvature is
obtained using equation (4):
H
R
θ
=
(4)
where H is the height of the segment. The following
lengths are obtained from Fig. 10, based on the
segment curvature:
12
11 12
12
21 22
22
22
D
D
LR LR
D
D
LR LR
=+ =+
=− =−
(5)
where D1 and D2 are the diameters of the segment
end discs.
Based on the Carnot theorem, the lengths A1 and A2
are then obtained:
22 22
11112 1112
22 22
22122 2122
2cos
2cos
ALL LL
ALL LL
θ
θ
=+−⋅⋅⋅
=+−⋅⋅⋅
(6)
The control wires curvature radius R1 and R2 are
given by the relations (7):
12
12
2 sin 2 sin
22
AA
RR
θ
θ
==
⋅⋅
(7)
Finally, the lengths of the control wires are
obtained as in (8):
1
11
2
22
2sin
2
2sin
2
w
w
A
LR
A
LR
θ
θ
θ
θ
θ
θ
⋅
=⋅=
⋅
⋅
=⋅=
⋅
(8)
EXPERIMENTS WITH A CONTINUUM ROBOT STRUCTURE
201

Figure 9: Projection of the wire to get the
α
direction.
For the 3D case, a virtual wire is considered,
which gives the α direction of the curvature.
Considering one virtual wire in the direction of the
desired curvature having length calculated as below.
First, the following lengths are calculated:
)cos(
2
D
RL)cos(
2
D
RL
)cos(
2
D
RL)cos(
2
D
RL
)cos(
2
D
RL)cos(
2
D
RL
3
2
223
1
31
2
2
222
1
21
1
2
121
1
11
αα
αα
αα
⋅+=⋅+=
⋅+=⋅+=
⋅+=⋅+=
(9)
⎪
⎩
⎪
⎨
⎧
−°=
−°=
−=
αα
αα
αα
240
120
3
2
1
(10)
Based on (6) and (9) the curvature radius R1, R2
and R3 of the three control wires are then obtained.
Finally the lengths of the control wires are
calculated with relation (11):
θ
θ
θ
⋅=
⋅=
⋅
=
33w
22w
11w
RL
RL
RL
(11)
Besides, for the system presented we can obtain
two useful relations:
3
1
3
1
cos( ) 0
1
3
i
i
i
i
L
wL
α
=
=
=
=
⎧
⎪
⎪
⎨
⎪
⎪
⎩
∑
∑
(12)
The second equation can be utilized to estimate
the compression or the extension of the central bone.
4 EXPERIMENTS
We conducted a series of experiments, having as
purpose the analysis of the robotic structure,
including the behavior of the arm and the stepper
motors used for its actuation.
For these tests, we used the following equipment:
Spider 8 acquisition system, with eight input
channels and 12 bit resolution per channel
Nexus 2692-A-0I4 signal conditioner with load
compensation, four input/output channels,
frequency domain 0.1Hz ÷ 100KHz and linear-
ity error ≤0.05%;
Bruel&Kjaer model 4391 accelerometers,
frequency domain 0.3 ÷ 10000Hz, load 1 pC/ms-
2, linearity error ≤1%;
Figure 10: Recorded dataset. Marked with black - the
current, with red - end effector oscillation and with blue -
the displacement.
Figure 11: Recorded data for a movement executed at
19.23 mm/s.
Figure 12: Frequency analysis for oscillation. Slow speed
case.
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
202
WA300 inductive transducer for linear
displacement, displacement range 0÷300mm,
linearity error ≤1%;
MicroSwitch model CSLA 20KI current
transducer, current domain ±20A, linearity
error ≤1%
The data was recorded on a IBM notebook with
Testpoint V5.1 soft-ware installed
We placed the sensors as follows:
Figure 13: Medium speed movement (156.99 mm/s).
The displacement sensor was connected at the
robot’s arm free end. The objective is to
measure the total displacement realized by the
end effector. Because of the sensor’s intrinsic
structure, and for obtaining a linear relation
between sensor measurement and robot
displacement in the 3D space, we restricted the
robot’s movement to a movement in a plane
formed by the robot’s backbone and the
sensor’s extension axis
The accelerometer was placed in the same
point as the displacement sensor. The objective
is to determine the vibration induced in the
robot arm structure by the actuation system and
the control algorithm.
The ammeter was connected in a serial mode
with one of the stepper motor phases (the
stepper motors are tree phases ones). The
objective is to determine the stepper motor
current need during the movements, and also to
detect if and when the losing steps
phenomenon occurs, based on the fact that a
losing step process can be noticed by observing
a high current peak.
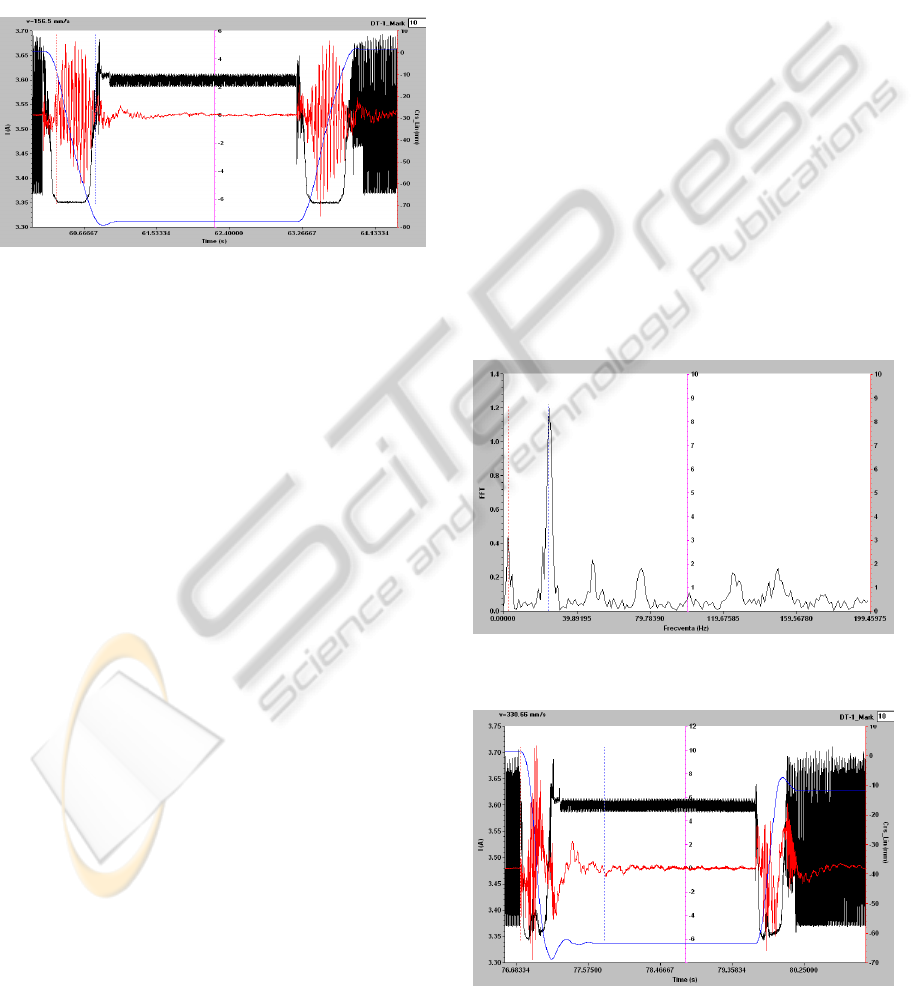
In the figure 10 can be observed a recorded
dataset. The measured current is represented with
black color, with blue is represented the arm
displacement, and with red is marked the oscillation
recorded at the end of the robot arm. The dataset
recorded a same trajectory described by the robot,
but at different speeds. In the left side can be
observed the movement execution at a lowest speed
(19.23 mm/s), and in the right side at high speed
(330 mm/s). In the following paragraphs we will
analyze the robot’s behavior for these two extreme
movements. The first move observed was executed
with a speed of 19.23 mm/s, going forward from the
origin to the end point and, after a short break, back
to the original. The detailed recorded data can be
seen in the Figure 11.
The oscillation was amplified 100 times, for
having a better view for its evolution. As expected
for slow moves case, when the effort needed for
robot arm displacement is low, the current evolution
indicates that the stepper motor doesn’t lose any
steps and the movement there is no position error.
Regarding oscillation, one can observe that near the
origin position the robot exhibits a higher oscillation
of its end effector. We consider that this
phenomenon appeared due to the fact that near
origin the tension in the actuation cables is lower,
because the potential energy due gravity have the
lowest value, and at end point the potential energy
have a considerable higher value, conducting to a
higher tension in cables which prevents the robot
arm to oscillate.
Figure 14: Frequency analysis for oscillation. Medium
speed case.
Figure 15: High speed movement.
EXPERIMENTS WITH A CONTINUUM ROBOT STRUCTURE
203

If we take a closer look at the oscillation, and
make a frequency analysis (figure 12), it can be
observed that there are two spikes in frequency, one
at 2.9 Hz, and one at 159.99 Hz.
Figure 16: Frequency analysis for oscillation. High speed
case.
As already identified, where an artificial vision
system was used (Tanasie et al., 2009), the first
spike at 2.9 Hz represents the natural resonance
frequency for the robotic arm. By observing the
oscillation analysis for faster movements, we
determined that the second spike, with a higher
level, placed at 159.99 Hz, is induced by the
actuation system – the vibrations frequency
generated by the actuation system and transmitted in
the cables, also being responsible for the resonance
spike at 2.9 Hz.
Considering a medium speed movement (156.99
mm/s), the following dataset was recorded (Figure
13). Analyzing the current evolution, a singular
spike can be observed at 63.8 second on the
timescale, which indicates that the motor loses a
single step, this situation being caused by the fast
stop of the robotic arm. Correlated with this fact, the
analysis of the trajectory evolution shows that the
end of the robot arm don’t stop directly at the
desired position, and under the effect of inertia
determined by its own mass it passes that position.
While the cables exhibit neither compression nor
extension, the position error is determined
exclusively by a shear effect. Shear is an elastic
deformation, thus generating a force that brings the
robot arm back at the desired position. This
transitory effect takes 0.2 seconds and the maximum
position error is 2 millimeters.
The oscillation graph shows a similar evolution
as described for the previous case, but the frequency
analysis gives a different characteristic (Figure 14).
The natural oscillation frequency can be identified as
a spike at the same frequency 2.9 Hz, but the
vibration induced by the actuation system may be
found now at 24.6 Hz, as a result of the motor’s
speed variation.
The last observed evolution is for high speed
movement (330 mm/s). The recorded data is
represented in the Figure 15. The current evolution
is more dramatic and irregular, as can be observed in
the figure 15 (marked with black line). The current
profile isn’t anymore smooth, as in previous cases,
and some major fluctuations can be seen at 76.9 sec
and at 79.7 sec. Those fluctuations correspond to a
large number of lost steps, the effort required for
moving the robot being very large. This conclusion
is sustained by the conclusions of analysis conducted
for displacement and vibration. Regarding the
displacement, the robot was programmed to execute
the very same movement, going from origin to a
desired position and then back to the origin, but at
different speeds. This means that in all recorded
data, the robot must achieve the same desired
position, and the position at the end of the
movement must be the same with the position from
where the movement started (the origin). Observing
the displacement from figure 15 (marked with blue
line), it can be determined a difference of 12 mm
between the beginning position and final position.
Also, if one compares the desired position achieved
in figure 11, 13 and 15, can determine that the
desired position is achieved successfully in figure 11
and 13, but in figure 15 the robot fails to reach the
desired position, introducing a position error of 6
mm. The inertial effect is very high, the robot
presenting a large oscillation before remaining
steady in the desired position. Previous conclusions
are also sustained by the recorded vibrations,
marked with red line in figure 15. On the same
timeline with the current fluctuations can be noticed
a large amplitude of the vibration, as an effect of the
discontinuity in movement determined by lost steps.
Moreover, as the frequency analysis shown in the
figure 16 denotes, this high speed actuation
determines a resonance with the natural frequency of
the robot arm, affecting the robot arm evolution.
5 CONCLUSIONS
As conclusions, for the slow speed moves, there are
no lost steps in stepper motors, meaning that an open
loop control can be successfully applied to the
system. There is a low amplitude oscillation of the
robot’s arm, mainly at 159.99 Hz, induced by the
actuation system, but it induces only a small
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
204

amplitude natural frequency resonance, so the robot
arm doesn’t resonate with actuation system. Also,
considering the displacement (marked with blue in
the figure), it can be observed that the position error
is zero. The overall behavior of the structure is a
very good one.
For the medium speed moves, the stepper motors
may lose steps, but this phenomenon occurs
occasionally and can be considered insignificant if is
evaluated as a ratio lost steps / total number of steps,
meaning that an open loop control can still be
successfully applied to the system. There is a low
amplitude oscillation of the robot’s arm, mainly at
24.6 Hz, induced by the actuation system, but it
induces only a small amplitude natural frequency
resonance, so the robot arm doesn’t resonate with
actuation system. The displacement record reveals a
transient evolution around the final position,
introducing a transient position error, having 2 mm
maximum amplitude and with a short duration, 0.2
seconds. At the end of the transient evolution, the
robot stops on the desired position and the position
error is zero. The overall behavior of the structure is
a good one.
ACKNOWLEDGEMENTS
The research presented in this paper was supported
by the Romanian National University Research
Council CNCSIS through the IDEI Research Grant
ID93 and by FP6 MARTN through FREESUBNET
Project no. 36186.
REFERENCES
Blessing, M., Walker, I. D., 2004. Novel Continuum
Robots with Variable- Length Sections, Proceedings
3rd IFAC Symposium on Mechatronic Systems,
Sydney, Australia, September 2004, pp. 55-60.
Boccolato, G., Manta, F., Dumitru, S., Cojocaru, D., 2009.
3D Control for a Tentacle Robot, 3rd International
Conference on Applied Mathematics, Simulation,
Modelling (ASM'09), Vouliagmeni Beach, Athens,
Greece.
Cojocaru, D., Tanasie, R. T., Marghitu, D. B., 2008. A
Complex Mathematical Expression Operations Tool,
Annals of The Univ. of Craiova, Series: Automation,
Computers, Electronics And Mechatronics, ISSN:
1841-0626, Volume 5(32), no. 1, pp. 7-12.
Cowan, L. S. and Walker, I. D., 2008. “Soft” Continuum
Robots: the Interaction of Continuous and Discrete
Elements, Artificial Life XI.
Crespi, A. and Ijspeert, A. J., 2006. An amphibious snake
robot that crawls and swims using a central pattern
generator. 9th International Conference on Climbing
and Walking Robots (CLAWAR 2006), pp19-27.
Dumitru, S., Cojocaru, D., Dumitru, N., Ciupitu, I.,
Geonea, I., Dumitru, V., 2009. Finite Element
Modeling of a Polyarticulated Robotic System, Annals
of DAAAM, ISSN 1726-9679, pp 969.
Ivanescu, M., Cojocaru, D., Popescu, N., Popescu, D.,
Tănasie, R.T., 2006. Hyperredundant Robot Control
by Visual Servoing, Studies in Informatics and
Control Journal, Volume 15, Number 1, pp93-102,
ISSN 1220-1766.
Robinson, G., Davies, J. B. C., 1999. Continuum robots—
A state of the art. IEEE International Conference on
Robotics and Automation, pp2849–2854. Detroit, MI.
Suzumori, K., Iikura, S., Tanaka, H., 1991. Development
of Flexible Microactuator and its application to
Robotic Mechanisms, Proceedings of the IEEE
International Conference on Robotics and Automation,
pp. 1622-1627.
Tanasie, R. T., Ivanescu, M., Cojocaru, D., 2009. Camera
Positioning and Orienting for Hyperredundant Robots
Visual Servoing Applications, Journal of Control
Engineering and Applied Informatics, Vol 11, No 1,
p19-26, ISSN 1454-8658.
EXPERIMENTS WITH A CONTINUUM ROBOT STRUCTURE
205
