COLOR IMAGE ENCRYPTION SOLUTION BASED ON THE

CHAOTIC SYSTEM OF LOGISTIC AND HENON

Zhang Yunpeng

, Sun Peng

, Xie Jing

and Huang Yunting

College of Software and Microelectronics, Northwestern Polytechnical University

P.O.Box 732, 127#, West YouYi Road, Xi’an, 710072, China

College of Computer, Northwestern Polytechnical University, 127#, West YouYi Road, Xi’an, 710072, China

Keywords: Cryptography, Chaotic system, Color image, Encryption.

Abstract: The security of color image has become an important network information security research field. To meet

the security requirements of color image and according to the characteristics of the image coding and

chaotic system, the paper presented a color image encryption solution based on the chaotic systems. With

the help of Logistic system, the solution generates the chaotic sequence, which is used to the parameters and

the number of iterations of Henon system. And then, encrypt the color image through multiple iterating the

Henon system. At last, we analyse and prove the solution in theory and experiment. The results show that

the encrypted image has a uniform distribution of the pixel value, has a good solution diffusion, can

effectively resist the phase space reconstruction attacks, and has a good security and reliability.

1 INTRODUCTION

At present, the conventional image encryption

solutions based on chaotic revealed many security

risks, mainly showed in the weakness of lacking of

ability to resist against the common attack methods.

In literature (Li, SJ, Zheng, X 2002, et al), the

security of image encryption solutions were

explored and analyzed. Meanwhile, showed the

weakness that some solutions are difficult to resist

the common attacks. In literature (Li, Q, Zhao, K, et

al 2007, p.45), Li Quan etc successfully deciphered a

chaotic image encryption solution by using the phase

space reconstruction method and the method of

exhaustion. To solve these problems, some scholars

made some methods resist conventional attacks

during designing image encryption solutions. For

example, Wu Xu etc proposed a method through

introducing an auxiliary key to resist the known

plaintext in the process of image encryption (Wu, X,

Chen, ED & Hu, JS* 2004, p.754), but it could do

nothing to the emerging phase space reconstruction

attacks. The solution in this paper is mainly used in

the two-dimensional chaotic system, and it applied T

generated in the encryption process as one of the

decryption keys in the decryption process. Expect

the final solution can be effective against the phase

space reconstruction attacks.

2 PROGRAMME DESCRIPTION

The chaotic systems (Logistic(Pareek, NK, Vinod, P ,

Sud, KK 2006, p.926

), Henon (Zhang, H, Wang, XF, et al

2005, p.2137

) and Arnold (Zou, JC, Tie XY 2000,

p.182

) ) this paper have used are suitable to

encryption solution, which has been recognized by

scholars in the field of Chaos.

Input: original image I (size r×r

encryption key (a，b，

，

Where a, b for the Arnold transformation parameters;

，

for the Logistic system parameters.

1. In the original image I (r×r), the gray value of

each pixel is A(x,y). Make the image into a

linear character array, for

A(x,y)= A

(r*x+y),

that

is, the gray value of each point in turn recorded

as A

，A

，…,A

，n=r×r.

2. By the

，

of secret key, using logistic

system formula generates real-valued chaotic

sequence P = {p

| i，j= 0，1，2，… ，N - 1 }, and

generates the integers sequence D = {d

| i = 0，

275

Yunpeng Z., Peng S., Jing X. and Yunting H. (2010).

COLOR IMAGE ENCRYPTION SOLUTION BASED ON THE CHAOTIC SYSTEM OF LOGISTIC AND HENON.

In Proceedings of the 5th International Conference on Software and Data Technologies, pages 275-278

DOI: 10.5220/0002923602750278

 SciTePress



1，2，…，N-1，d

∈[2,3,4, …,62]}; here, if

the scope of d takes 1, it Will be broken by

exhaustive key flow; if the scope of d is too

large, iterative process will lead to be

time-consuming. If the scope of d takes 0, the

number of iterations takes 0, so pixel value does

not get encrypted. Through several experiments,

ultimately determine d is able to combine the

efficiency and safety in the above scope. The

specific description of generating method is in

the back for the two sequences.

3. The gray-scale transformation matrix generated

by the P: G = {gij | gij

∈

[0,1,2, …,255]； i，j =

0，1，2，…，N-1}；

4. Using Arnold formula, key a, b for the

parameters, we can get the image I' after the

Arnold scrambling transformation of the

original image I. Set

（

，

） for the

horizontal and vertical coordinates before the

transformation of the first pixel. Set

（

，

y ）

for the horizontal and vertical coordinates after

the transformation of the first pixel. Similarly,

（

，

），（

，

y ）for the horizontal

and vertical coordinates before and after the

transformation of the K pixel. shown in Figure

Figure 1: Transformation process.

5. Encrypt a image through iteration encryption by

using Henon system. The number of iterations d

determined by the generated chaotic sequence in

step 2, the parameters of Henon system which a

= 2, b = 1. Concrete steps are as follows:

1) Order

, Y

.let X

，Y

have

d1 iterative times by using Henon system, get

，Y

and then make X

assign

2) Order X

， Y

, let X

have d

iterative times by using Henon system, get X

，

, and then make X

assign

A .

3) This chain iteration, order X

k+1

let X

k+1

，Y

k+1

have d

k+1

iterative times by using

Henon system, get X

k+1

，Y

k+1

, and then make

k+1

assign

4) Until the order X

n-1

n-2

, Y

n-1

A , let

n-1

，Y

n-1

have d

n-1

iterative times by using

Henon system, get

n-1

，Y

n-1

, and then make

n-1

assign

−

5) Order X

= Y

n-1

，Y

, let X

have

iterative times by using Henon system, get

，Y

, and then make X

assign

A , make

assign T.

So we can get

，

A 3

，…,

that are encrypted plaintext by Henon

system. T is used as one of the decryption keys

in the decryption process..

5. Gray-scale transformation matrix generated

according to the general linear pixel was

recorded as G1, G2, ..., Gn.

Make

and

the corresponding Gi do the bitwise XOR

operation, get

. As shown in Figure 2:

Figure 2: Gray matrix XOR process.

，

A 3

，…,

are

encrypted ciphertext which are got by XOR

operation. It is also the final encrypted plaintext.

Then make

A revert to grayscale value matrix.

So we got the encrypted image

Output: encrypted image I*，T.

Decryption process is the inverse of the encryption

process, here no longer explain.

ICSOFT 2010 - 5th International Conference on Software and Data Technologies

276

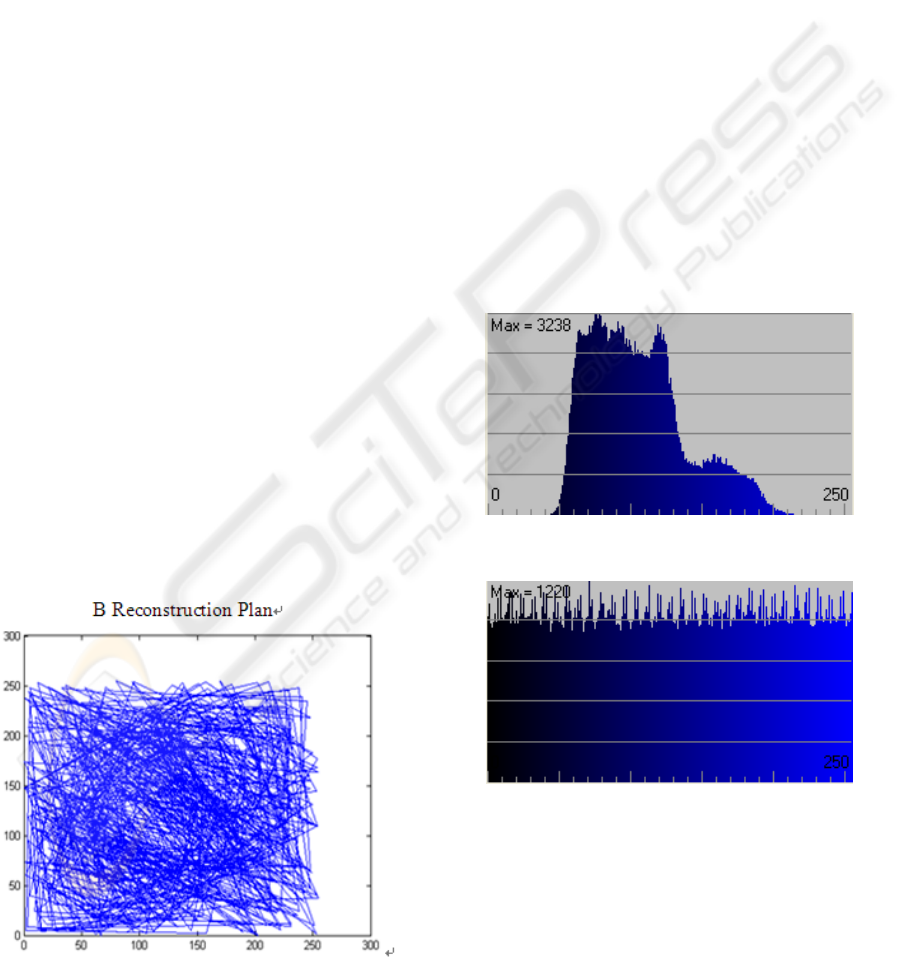
3 EXPERIMENTAL RESULTS

AND PERFORMANCE

ANALYSIS

3.1 Analyse the Phase Space

Reconstruction Attacks

Phase space reconstruction break method means: If

the chaos encrypted image is a ciphertext which is

computed directly with the plaintext image pixels

and the corresponding chaotic sequence value, the

pixel value of the ciphertext after computing must

retain the characteristics of the chaotic equation in

the data features, the reason of which is that the

pixel value of the plaintext image pixels changes

more relaxed, but the changes of chaotic sequence

are larger. We can determine which kind of kinetic

equation the encryptor has used, as long as we can

re-drawed Phase space diagram of the ciphertext,

and find out the most similar one in the dynamic

characteristics through the comparison with the

original phase space diagram of all kinds of chaos

dynamics equations. Based on the idea, some

scholars (

Li, Q, Zhao, K, et al 2007, p.45) proposed

some successful examples that using phase space

reconstruction method deciphers stream cipher

encryption method based on chaotic sequence. This

section conducted phase space reconstruction to a

ciphertext generated in the solution by the use of

delay time and embedding dimension, based on the

method of attack proposed in the literature. The

results shown in Figure 3

（Just B Component, G and R

Component have been omitted.

Figure 3: B Component of the Phase Space

Reconstruction.

From the above diagram, it is not difficult to see

that there's no meaning of the reconstructed phase

space, and we can not derive any useful information

of the chaotic system. So, the encryption solution

based on chaotic system proposed in this paper has a

very strong immune to the attack methods based on

phase space reconstruction.

3.2 Statistical Characteristics of

Histogram Analysis

Figure 4 shows the histogram statistics of the B

component of the original color map. It can be easily

seen that, the distribution of Blue primary colors is

extremely uneven. While Figure 5 shows the

histogram statistics of the encrypted color image.

Obviously, the histogram of the encrypted image and

the original are very different. The histogram of the

encrypted image is very uniform. It is far better than

the original and covers the distribution law very well.

Therefore, this algorithm can effectively resist

statistical attacks.

Figure 4: Lena image statistic histogram (B).

Figure 5: Encrypted Lena image statistic histogram (B).

3.3 Comparison with other Similar

Solutions

The proposed solution in this paper, although its

scrambling encryption based on Arnold system can

be similarly cracked, as generating decryption

parameter T which is depends on the plaintext in the

COLOR IMAGE ENCRYPTION SOLUTION BASED ON THE CHAOTIC SYSTEM OF LOGISTIC AND HENON

277

second part of the encryption process, so it is

difficult to obtain the parameter of the second part.

Even if we obtained the parameter in the second part,

but we do not know the iterative times and

encryption procedure, we also can not calculate the

parameter T. Therefore, compare with the analyzed

solutions in literature (

Cahit, C, Ercan, S 2008), the

solution in this paper is more safety.

4 CONCLUSIONS

This paper proposed a color image encryption

solution based on Logistic and Henon chaotic

system. Theoretical analysis shows the new solution

has a good diffusion and it can effectively resist

phase space reconstruction; experiment verification

and analysis explain solution method have good

statistical characteristics of histogram and the

distribution of encrypted pixel value is uniformity;

compare with some solutions which are proposed in

literature, we can know that the solution has good

safety and reliability.

ACKNOWLEDGEMENTS

This work is supported by Aero-Science Fund of

China (2009ZD53045), and Innovation Project of

Northwestern Polytechnical University (W016141).

REFERENCES

Li, S J, Zheng, X 2002, ‘On the security of an image

encryption method [A]’, Proceedings of IEEE 2002

International Conference on Image Processing[C].

Omni Press, pp.453-487.

Li, S J, Zheng, X 2002, ‘Cryptanalysis of a chaotic image

encryption method [A]’, Proceedings of IEEE 2002

International Symposium on Circuits and Systems [C].

Phoenix-Scottsdale: Omni Press, pp. 231-262.

Wu, X, Chen, E D & Hu, J S* 2004, ‘An improved chaotic

image encryption method’, Journal of Dalian

University of Technology, vol.44 (5), pp. 754-757.

He, X P, Zhu, Q S & Gu, P 2006, ‘A New Chaos-Based

Encryption Method for Color Image’, RSKT, vol.4062,

pp. 671–678.

Li, Q, Zhao, K, et al 2007, ‘Research on Deciphering

Method of a Kind of Chaotic Encrypting Picture’,

Journal of National University of Defense Technology,

vol. 29(3), pp. 45-49.

Pareek, N K, Vinod, P, Sud*, KK 2006, ‘Image encryption

using chaotic logistic map’, Image and Vision

Computing, vol.24, pp. 926–934.

Zhang, H, Wang, X F, et al 2005, ‘A fast image encryption

algorithm based on chaos system and henon map’,

Journal of Computer Research and Development,

vol.42(12), pp.2137-2142.

Zou, J C, Tie X Y 2000, ‘Arnold transformation of digital

image with two dimensions and its periodicity’, North

China University of Technology, vol.25 (5),

pp.182-189.

Cahit, C, Ercan, S* 2008, ‘Cryptanalysis of a chaos-based

image encryption algorithm’, Physics Letters A, vol.11

(25).

ICSOFT 2010 - 5th International Conference on Software and Data Technologies

278