A MULTI-ESTIMATION SCHEME FOR CONTROLLING
THE BEVERTON-HOLT EQUATION IN ECOLOGY
S. Alonso-Quesada and M. De La Sen
Department of Electricity and Electronics, Faculty of Science and Technology, University of the Basque Country
Campus of Leioa, 48940-Leioa, Bizkaia, Spain
Keywords: Adaptive control, Beverton-Holt Equation, Carrying capacity, Control systems, Multi-estimation.
Abstract: This paper proposes an adaptive control algorithm to govern the solution of the Beverton-Holt equation
under parametrical uncertainties and the potentially presence of additive disturbances. The control strategy
is based on a multi-estimation scheme with a supervisor choosing on-line the active estimation model used
to parameterize the controller. The tracking of a reference sequence with local modifications of the carrying
capacity sequence around its nominal values is achieved with such a control strategy.
1 INTRODUCTION
Models based on the Beverton-Holt Equation (BHE)
are very common in Ecology for the study of the
evolution of species in their habitats, (Barrowman et
al., 2003). Such models rely on more general
discrete recursive equations proposed in (Stevic,
2010, Elsayed and Iricanin, 2009, Iricanin and
Stevic, 2009a, 2009b). The BHE is a nonlinear
equation given by (Beverton and Holt, 1957):
()
kkk
k1
kk k
x
{
Kx
x
K1
+
μ
=
+μ−
,
}
0
k:∈=∪NN0
0
(1)
where
N is the set of natural numbers, the
initial species population size, and
0
x>
k1
x
k
x
+
the
population sizes at time instants kT (
spawning stock)
and (k+1)T (
recruitment), respectively, with T being
the sampling period, and
{
}
:0∪
k0
++
μ∈ =RR
and
the population
intrinsic growth rate and
the
environment carrying capacity at the time instant
kT, respectively, with
k
K ∈
+
R
+
R
being the set of positive
real numbers. The intrinsic growth rate sequence
is determined by life cycle and demographic
properties like species growth rate, survivorship rate
and so on. The carrying capacity sequence
{
{}
k
0
∞
μ
}
k
0
K
∞
is
a characteristic of the habitat depending on resources
availability, temperature, humidity and so on.
Typically,
k
1
μ
>
and so
{
as
}
k
0
∞
μ
{}
k
0
K
∞
are
cyclic sequences as a consequence of periodic
fluctuations are common in biological problems. The
carrying capacity sequence is susceptible of being
locally modified by means of small changes of
temperature, humidity and so on around nominal
values. This fact can be used to control the species
population size in a closed or semi-closed habitat
(De la Sen and Alonso-Quesada, 2008, De la Sen
and Alonso-Quesada, 2009). Such control strategies
take advance of the linearity of the Beverton-Holt
inverse equation (BHIE) (Stevic, 2006) so that
conventional techniques developed for linear control
systems may be used in order to govern the BHIE
solution and then also the BHE one. In such works,
the controllers are designed for matching a
prescribed reference model by the BHE model
possibly affected by the presence of additive
disturbances. The reference models are another BHE
with suitable intrinsic growth rate and carrying
capacity sequences. The paper (De la Sen and
Alonso-Quesada, 2008) considers the perfect
knowledge of the sequences defining the standard
BHE while the research in (De la Sen and Alonso-
Quesada, 2009) extends the discussion to the
adaptive case since the intrinsic growth rate and
carrying capacity sequences are partially or fully
unknown. In both cases the environment carrying
capacity may be locally modified around its
reference values to achieve the prescribed behaviour.
133
Alonso-Quesada S. and De La Sen M. (2010).
A MULTI-ESTIMATION SCHEME FOR CONTROLLING THE BEVERTON-HOLT EQUATION IN ECOLOGY.
In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 133-140
DOI: 10.5220/0002927201330140
Copyright
c
 SciTePress

The matching objective by local modifications of
the carrying capacity sequence is only available and
practical if the BHE to be controlled as well as the
BHE used as the reference model are locally
deviated from each other. However, such a condition
may not be guaranteed, at least in an adaptive
control context where some system parameters are
unknown. In this sense, the
main contribution of the
present paper lies in the
design of an adaptive
control scheme with a set of potential reference
models, instead of a unique one, to be matched in
order to circumvent such a drawback.
For such a
purpose,
the reference models included in the set are
suitably chosen such that at least one of them is
sufficiently closed to the unknown BHE at any
sampling time.
This quality may be guaranteed with
the inclusion of
a large number of reference models
in the control scheme and a well distribution of them
within the BHE parameters space.
An estimation
algorithm is associated to each reference model.
Such estimators work in parallel and a supervisor
activates on-line the estimation algorithm providing
the closest estimated model to the unknown BHE at
each sampling instant. The closeness is measured by
means of the estimation error associated to each
algorithm.
The supervisor function implies the
switching among the estimated models provided by
the estimators included in the adaptive control
scheme. Then,
a minimum residence time is
maintained in operation the active estimated model
in order to achieve a good tracking behaviour and
the stability of the control system
(De la Sen and
Alonso-Quesada, 2006, Narendra and Balakrishnan,
1997). In this way, the adaptive control scheme
works with a time-varying reference model, what is
compatible in a species population system subject to
periodic fluctuations.
2 PROBLEM STATEMENT
The change of variable in (1) leads directly
to the BHIE (Stevic, 2006):
1
kk
sx
−
=
k1 k k k k
sasbu
+
=+
,
1
00
sx
−
=>0
(2)
where ,
1
kk
a
−
=μ
kk
b
1a=−
and
1
kk
uK
−
=
0
k
∀
∈N
.
Note that the inverse carrying capacity can act as a
control action. If an additive disturbance sequence
{
}
0
k
0
∞
η exists, one gets a more general version of (2):
()
k1 k k k k k
sasuu
+
=−++
0
η
(3)
The disturbance may include the effects in the
solution of parametrical uncertainties, for instance,
in the intrinsic growth rate, or effects, like
migrations or local migrations which are not taken
into account in the standard BHE. The following
assumptions are considered related to the BHE:
Assumptions 1.
(i)
k
1
μ
+
ε≤μ<∞
and
Kk
K
ε
≤<∞
and
some
0
k∀∈N
K
,
+
μ
εε∈R
.
(ii)
0
kk
η
≤η <∞
0
k
∀
∈N
with
{}
k
0
∞
η
known. ***
Remark 1.
(i)
The BHIE is stable and controllable since both
k
1
a1
1
μ
≤
<
+ε
and
k
b
0
1
μ
μ
ε
≥>
+ε
are
derived from Assumption 1(i).
0
k∀∈N
(ii) All solutions of the BHE and BHIE are
uniformly bounded and positive provided that
if both Assumptions 1 hold (De la Sen and
Alonso-Quesada, 2009). ***
0
x0>
Since the control action is the inverse of the
environment carrying capacity it is not admitted a
large deviation from its nominal values for tracking
purposes in a practical situation. That means that the
reference model to be matched by the current BHE
has to be sufficiently closed to it. Such a reference
model might be another BHE as follows:
()
***
*
kkk
k1
** *
k
x
0
k∀∈N
kk
Kx
x
K1
+
μ
=
+μ−
(4)
which defines the suitable solution through the
appropriate reference values of the intrinsic growth
rate and the environment carrying capacity
sequences,
{
}
*
k
0
∞
μ and
{
}
*
k
0
K
∞
with
. Its corresponding reference BHIE is:
*
k
1μ>
0
k∀∈N
****
k1 k k kk
sasb
+
=+r
(5)
with reference input , and parameter
sequences
()
1
*
kk
rK
−
=
(
)
1
**
kk
a
−
=μ
and .
(
b1=−
)
1
**
kk
μ
−
0
k∀∈N
}
*
K
Assume that the carrying capacity
{
k
0
∞
and
the intrinsic growth rate
{
}
*
k
0
∞
μ
sequences of a
reference BHE are given together with the sequences
{}
k
0
∞
δ
and
{}
k
0
∞
λ
, with
δ∈
and
[
)
0, 1
k
*
k
1
0, λ∈
⎢
k
⎡⎞
⎟
μ
⎣⎠
0
k
∀
∈N
. The following definition and proposition
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
134

are concerned with the available BHE models for
tracking, with a sufficiently small tracking error, a
given BHE reference solution by local modifications
of the environment carrying capacity (De la Sen and
Alonso-Quesada, 2009).
Definition 1. A class of BHEs
exists parameterized by some sequences
{
()
**
BHE k k k k
K, , ,μδλ^
K
}
k
0
∞
and
such that
{}
k
0
∞
μ
**
k
kk
1
, K
⎡⎤
δ
⎢⎥
λ
k
kk
1
KK
11
−δ +
∈
+λ −
⎣
k
⎦
and
()()
**
kkkk
**
kk kk
11
,
11
⎡⎤
+λ μ −λ μ
⎢⎥
+λ μ −λ μ
⎢⎥
⎣⎦
k
μ∈
. ***
0
k∀∈N
Proposition 1. If (i) the upper-bound sequence
{}
k
0
∞
η
for the absolute value of the additive
disturbance
{
}
0
k
0
∞
η
of the BHIE associated to a BHE
belonging to the class is such
that
()
**
BHE k k k k
K, , ,μδλ^
()
()
*
kk
kk
δμ
+δ μ
k
**
k
1
1K
−
η≤
0
k
∀
∈N
(
*
00
ss1≥−
and (ii) the initial
condition fulfils for some
monotonically increasing sequence
{
0
s
)
0
0γ>
}
k
0
∞
γ
with
, and such that
k
γ∈
+
R
k
1γ<
0
k∀∈N
0
kN
Max
∈
2
k0
2
12
⎧⎫
⎡⎤
⎛⎞
⎪⎪
≤γ
⎜⎟
⎨⎬
⎜⎟
⎢⎥
⎪⎪
⎝⎠
⎣⎦
⎩⎭
k
δ+
1
⎢
+δ ε
1
ε−
⎥
<
+
μ
μ
, then:
(i) The control law:
()
kk k k k k
*
k
kk
kk
2
t r f s if s
u
1K
r otherwise
⎧
+−ω ≤
⎪
=
+δ
⎨
⎪
−ω
⎩
(6)
with the parameter sequences given by:
*
k
k
k
1a
t
1a
−
=
−
; ;
kk
f1t=−
k
k
k
1a
η
ω=
−
(7)
guarantees
**
kk
kkk
⎤
⎥
0
k∀∈N
kk
11
, K
11
⎡
−δ +δ
∈
⎢
+λ −λ
⎣⎦
KK
,
(ii) , where
{
()
*
kk k
ss1≥−γ
0
k∀∈N
}
k
0
s
∞
is the
solution of the BHIE and
{
}
*
k
s
0
∞
the solution of the
inverse of the reference BHE of the class
and
()
**
E k k k k
K, , ,μδλ
BH
^
(iii) the BHE solution
{
is upper-bounded by
the sequence
}
k
0
x
∞
*
k
k
0
x
1
∞
⎧
⎫
⎨
⎬
⎩⎭
−γ
, where
{
}
*
k
0
x
∞
is the
solution of the reference BHE of such a class. ***
Remark 2. Proposition 1 implies that given any
BHE belonging to an arbitrary class
, local modifications of the
carrying capacity around the reference sequence
(
**
BHE k k k k
K, , ,μδλ^
)
{
}
*
k
0
K
∞
can be used to achieve the control objective.
Namely, a sufficiently small tracking error between
the solutions of the given BHE and that of the
reference one of such a class can be obtained. ***
3 ADAPTIVE CONTROL
An estimation scheme is incorporated to solve the
control problem in the case that the intrinsic growth
rate sequence
{}
k
0
∞
μ
of the BHE (or the sequence
{}
k
0
a
∞
of the BHIE) is unknown. In the context of
adaptive control, the BHIE (3) can be written as:
(
)
k1 k k k k
sasuu
+
=
−++
η
(8)
for some unknown constant with
{
1
a
−
=μ
}
k
0
∞
η
given by:
(
)
(
)
0
kk kk
:a as u
k
η
=− −+η
(9)
In this way, the nominal parameter a of the
BHIE is constant and
{
incorporates the
deviations of the intrinsic growth rate with respect
to the unknown constant and, possibly, other
unstructured disturbance contributions in
{
}
k
0
∞
η
μ
}
0
k
0
∞
η
. If
k
0
η
≡
, the resulting particular case of (8) is called
the nominal BHIE.
The estimation algorithm provides an estimated
BHIE given by:
(
)
k1 k k k k
ˆˆ
sasuu
+
=
−+
(10)
where denotes the estimate of a at the k-th
sample. Moreover, an estimation error given by:
k
ˆ
a
(
)
k1 k1 k1 k k k k
ˆ
e:s s asu
+++
=
−=− −+η

(11)
A MULTI-ESTIMATION SCHEME FOR CONTROLLING THE BEVERTON-HOLT EQUATION IN ECOLOGY
135

is associated to the estimation algorithm where
is the parametrical error. Finally, the
tracking error between the solution of the BHIE to
be controlled an that of the reference model (5) is:
kk
ˆ
a:a a=−

**
k1 k1 k1 k1 k1 k1
ˆ
:s s e s s
+++++
ε= − = + −
+
)
(12)
The tracking error depends on the estimation
error and the deviation of the estimated model from
the reference one. Then,
the use of a multi-
estimation scheme and a supervisor choosing the
estimation algorithm providing the smallest
estimation error
, instead of the use of a unique
estimation algorithm,
will improve the tracking
objective
. Furthermore, the deviation between the
estimated model and the reference one can be
sufficiently small if (i) each estimation algorithm is
associated to a different BHE reference model
defining a class and (ii) each
one includes a parameter projection for
guaranteeing the closeness of both corresponding
estimated and reference models. In this way,
if the
multi-estimation scheme is composed by a large
number of reference model/estimation algorithm
pairs and the reference models are well distributed
within the definition domain of
{
, then at least
one of the estimated models will be sufficiently close
to the unknown BHE to be controlled for all time
.
As a consequence, such an unknown BHE solution
will be able to track that of the reference model
associated to the estimation algorithm activated by
the supervisor by means of locally modification of
the environment carrying capacity around its
nominal values. Both reasons motivate the use of a
multi-estimation scheme with several estimation
algorithms working in parallel in the adaptive
control scheme. Furthermore, such a scheme makes
that the reference model to be tracked is online
changed by the supervisor, what is of interest for
ecologic system subject to periodic fluctuations.
(
**
BHE k k k k
K, , ,μδλ
}
k
0
a
∞
3.1 Multi-estimation Scheme
A set
{
}
e
S: 1, 2, , n= …
e
of estimation algorithms
working in parallel is considered. Each one is
associated to a different class
()
**
BHE k k k k
K, , ,
μ
δλ
.
All of them use a least-squares algorithm with a
parameters projection and a dead-zone. The
projection is used to obtain an estimation model
belonging to the corresponding class and the dead-
zone for dealing with the presence of potentially
disturbances affecting to the nominal BHIE. Each
algorithm is defined by:
(
)
()
(i) (i)
kk kk1
(i) (i)
k1 k
2
(i)
kk k
sue
ˆ
aa
1su
+
+
σ−
=+
+β −
(13.a)
{
}
() ()
() ()
(i) (i)
k1 k1
(i) *(i) (i) *(i)
(i)
k1 k k1 k
k1
(i) *(i) (i) *(i)
k1 k k1 k
(i) *(i) (i) *(i)
(i)
k1 k k1 k
k1
(i) *(i) (i) *(i)
k1 k k1 k
(i)
k1
ˆ
aProja
11
if a
11
11
= if a
11
a
++
++
+
++
++
+
++
+
=
−λ μ −λ μ
<
−
λμ −λμ
+λ μ +λ μ
>
+
λμ +λμ
otherwise
⎧
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎩
(13.b)
with
()()
()
(i) *(i) (i) *(i)
(i)
00 00
0
(i) *(i) (i) *(i)
00 00
11
ˆ
a, 0
11
⎡⎤
−λ μ +λ μ
⎢⎥
∈⊆
−λ μ +λ μ
⎢⎥
⎣⎦
, 1
where
(i) (i)
kkk
ˆ
ess
=
−
,
0
k
∀
∈N
and , is the
estimation error of the i-th algorithm at the sampling
instant kT. The real sequence
{
e
iS∀∈
}
(i)
k
β
0
∞
is such that
(i)
k
0
β
>
0
k
∀
∈N
and
{
}
(i)
k
0
∞
σ
a relative dead-zone
defined as:
()
(i) (i)
k1 k
(i)
(i) (i) (i)
k
k1
(i) (i)
k1 k
(i)
0 if e
21
if e
+
+
⎧
≤ς η
⎪
⎪
σ=
⎨
βς−−ς
⎪
>ς η
ς
⎪
⎩
(13.c)
for some prefixed real constants and
(i)
1ς>
(
)
(i) (i)
1
0, 1
ς
∈ς−
where
{}
k
0
∞
η
is a known upper-
bound for
{}
k
0
∞
η
[see Assumption 1(ii)].
Such an algorithm meets the following
properties (De la Sen and Alonso-Quesada, 2009).
Lemma 1.
(i)
The sequence
{
}
(i)
k
0
ˆ
a
∞
is bounded and converges
asymptotically to a finite
(i)
ˆ
a
∞
,
(ii) The sequences
()
1/2
(i)
(i)
k
k1
2
(i)
kk k
0
e
1su
∞
+
⎧
⎫
⎛⎞
σ
⎪
⎪
⎜⎟
⎨
⎬
⎜⎟
+β −
⎪
⎪
⎝⎠
⎩⎭
and
()
1/2
(i)
k
k
2
(i)
kk k
0
1su
∞
⎧
⎫
⎛⎞
σ
⎪
⎪
⎜⎟
η
⎨
⎬
⎜⎟
+β −
⎪
⎪
⎝⎠
⎩⎭
are bounded and
both tend asymptotically to zero. ***
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
136

3.2 Supervisory System
This element chooses on-line one of the estimation
algorithms which compose the multi-estimation
scheme, namely, that closest to the unknown BHE.
For such a purpose, a cost function given by:
()
k
2
(i) k j (i)
kj
j0
Fe
−
=
=ρ
∑
(14)
with the forgetting factor , is
evaluated by the supervisor and
()
0,1ρ∈ ∩
+
R
0
k∀∈N
e
iS
∀
∈
and the estimation algorithm minimizing such a
function is activated. Furthermore, the supervisor
maintains activated such an algorithm at least a
minimum number of sampling periods before
switching to a different one. This residence time
prevents against the instability of the control system
caused by an eventual great amount of switches
concentrated in a short time interval. Then, the
switching law is given by:
min
N
{
k1 min
k
c if k k ' N
c
otherwise
−
−<
=

(15)
where is the sampling instant at which the last
switching occurred before the current time instant
and
k'T
kT
{
}
(i) (j)
ek k e
: Min i S F F i, j S=∈ ≤∀∈
.
3.3 Adaptive Control Law
An adaptive control law with the same structure as
(6)-(7) by replacing the true parameter by its
estimate and by deleting the correcting signal
for disturbances is used to generate the suitable
value for the carrying capacity sequence at each
sampling time. The super-index ( ) denotes the
estimation algorithm which is maintained active by
the supervisor at the current sampling instant kT.
The control term relative to the disturbances is
omitted since such disturbances are treated by the
inclusion of the dead-zone in each estimation
algorithm. Such a control law is:
k
a
k
(c )
k
ˆ
a
k
ω
k
c
()
()
()
k
k
kk k k k
(c ) *(c )
kk
k
-1
*(c )
k
2
t r s s if s
1K
u
K otherwise
⎧
−+ ≤
⎪
+δ
=
⎨
⎪
⎩
k
(16)
where
{
}
k
*(c )
k
0
K
∞
is the carrying capacity sequence of
the active reference model at the current sampling
instant and the sample-dependent controller
parameter is given by:
k
k
*(c )
k
(c )
k
1a
t
ˆ
1a
−
=
−
(17)
i.e., the control is parameterized from the active
estimated model at the current sampling instant.
3.4 Stability Analysis
The following additional assumption has to be
considered for proving the closed-loop stability.
Assumption 2. There exist known finite
nonnegative real constants and such that
1
ϑ
2
ϑ
{
}
k12 j
0jk
Max s
≤≤
η≤ϑ+ϑ
. ***
Remark 3. This assumption implies a slow growing
of the unknown disturbances with respect to the
solution of the BHIE. This is a reasonable
assumption used in adaptive control theory since a
complete lack of knowledge of disturbances makes
impossible the stabilization in the general case (De
la Sen and Alonso-Quesada, 2006, Feng, 1999).
The control system stability is based on the
following features:
(i) the adaptive control law (16)
with any of the estimation algorithms maintained
active by the supervisor for all time stabilizes the
control system while achieving a sufficiently small
tracking error if the unknown BHE is closed to the
reference BHE model corresponding to such an
estimation algorithm for all time by means of locally
modifications of the environment carrying capacity
(De la Sen and Alonso-Quesada, 2009), and
(ii) the
switching law in the supervisory system guarantees a
minimum residence time in the active estimation
algorithm, which is crucial to avoid instability
caused by an eventual high concentration of
switches in a short time interval (Narendra and
Balakrishnan, 1997). In summary, the switching law
allows to change the reference model to be tracked
by the current BHE to ensure the closeness between
such a BHE and the active reference one.
4 NUMERICAL EXAMPLE
A BHE (1) defined by an unknown intrinsic growth
rate sequence
{}
k
0
∞
μ
, which is given by:
A MULTI-ESTIMATION SCHEME FOR CONTROLLING THE BEVERTON-HOLT EQUATION IN ECOLOGY
137

k
1.65 if 360·j k<360·j+29
1.6 if 360·j+30 k<360·j+59
1.65 if 360·j+60 k<360·j+89
1.75 if 360·j+90 k<360·j+119
1.85 if 360·j+120 k<360·j+149
1.95 if 36
≤
≤
≤
≤
≤
μ=
0·j+150 k<360·j+179
2 if 360·j+180 k<360·j+209
1.95 if 360·j+210 k<360·j+239
1.85 if 360·j+240 k<360·j+269
1.8 if 360·j+270 k<360·j+299
1.75 if 360·j+300 k<360·j+329
≤
≤
≤
≤
≤
≤
1.7 if 360·j+330 k<360·j+359
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
≤
⎪
⎩
(18)
and a known nominal environment carrying
capacity sequence
{}
nom
k
0
K
∞
, given by:
nom
k
185 if 360·j k<360·j+29
180 if 360·j+30 k<360·j+59
185 if 360·j+60 k<360·j+89
200 if 360·j+90 k<360·j+119
205 if 360·j+120 k<360·j+149
210 if
K
≤
≤
≤
≤
≤
=
360·j+150 k<360·j+179
220 if 360·j+180 k<360·j+209
215 if 360·j+210 k<360·j+239
210 if 360·j+240 k<360·j+269
200 if 360·j+270 k<360·j+299
190 if 360·j+300 k<360·j
≤
≤
≤
≤
≤
≤ +329
185 if 360·j+330 k<360·j+359
⎧
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎨
⎪
⎪
⎪
⎪
⎪
⎪
≤
⎪
⎩
(19)
0
k, j∀∈N
, with as sampling period, is
considered. i.e., both are piecewise constant
periodic sequences with period equal to 1 year.
Note that each line of (18)-(19) corresponds to
values of the sequences during a month
approximately. The nominal carrying capacity
sequence is susceptible of locally modifications in
order to achieve the control objective. Such a
control objective is that the BHE solution
T1 day=
{}
k
0
x
∞
tracks a suitably chosen close reference sequence
{
}
k
*(c )
k
0
x
∞
with a sufficiently small tracking error. The
reference sequence is chosen on-line by a
supervisor among four potential sequences
{
}
*(i)
k
0
x
∞
,
for
{
}
e
iS∈=
(
:1, 2, 3, 4
, each one issued by the
BHE reference model defining a different class
)
(i) *(i)
BHE k
K,
*(i)
k
,μδ
(i) (i)
k k
,λ
. Such reference models
have been chosen so that at least one of them be
sufficiently close to the unknown BHE at each
sampling time. The four classes used in the example
are defined by the same carrying capacity
{
}
{
}
*(i) nom
kk
00
KK
∞
∞
=
,
{
}
(i)
k
0
∞
δ
(i)
k
and
{
sequences
with and and
}
(i)
k
0
∞
λ
526
k
(i)
k
0.0421δ=
e
iS
0.0λ=
0
∀∈N
∀
∈
and different sequences
{
}
*(i)
k
μ
*(3)
k
μ=
0
∞
2.05
for the
reference intrinsic growth rates, namely,
, , and
*(1)
k
1.55μ=
*(
k
*(4)
k
1.75μ=
k
2)
1.95μ=
0
∀
∈N
.
The unknown BHE to be controlled is
associated to the BHIE given by (8)-(9) with an
unknown parameter
a0.6
=
, which would
correspond to a constant intrinsic growth rate
1.6667
μ
=
. Such a parameter has to be estimated to
parameterize the adaptive control law (16) by using
(14), (15) and (17). For such a purpose, four
estimation algorithms working in parallel are
included in the multi-estimation scheme, each one
associated with each potential reference sequence
{
}
*(i)
k
0
x
∞
with
e
Si
∈
. Each algorithm is defined by
(13) with the same sequence
{
}
(i)
k
0
∞
β
, namely
(i) 10
k
10β= k
0
∀
∈N
(i)
1.011ς=
e
iS
, and the same parameters
and for all of them, i.e.
(i)
1
0.01ς=
∀
∈
. Moreover, the constants
5
210
1
−
ϑ= ×
and
6
2
10
−
ϑ=
(1)
0
ˆ
a0.6=
(4)
0
ˆ
a0.55=
are used to build the upper-bound of the
contribution of the unmodeled dynamics. The
estimation algorithms are, respectively, initialized
with , , and
. Note that each estimated model is
initialized within its corresponding class and they
cannot leave from them due to the projection
included in each estimation algorithm.
6
(2)
0
ˆ
a= 0.49
(3)
0
ˆ
a= 0.46
0
x
The initial population of the species is
300
=
and that of the reference sequence with
0
*(c )
0
x30= 0
0
c1
=
being the initialization for the switching law
of the supervisor. The results obtained with the
adaptive control system with the multi-estimation
scheme are displayed in the following figures.
Figures 1 and 2 show the time evolution of the
population size, active reference model solution and
tracking error sequences in a year approximately. An
acceptable tracking of the active reference by the
supervisor can be observed from such figures.
Figure 3 shows that local modifications of the
inverse of the environment carrying capacity are
sufficient to achieve such a tracking performance.
Note that the control sequence is within the domain
delimited by the lower and upper bounds associated
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
138

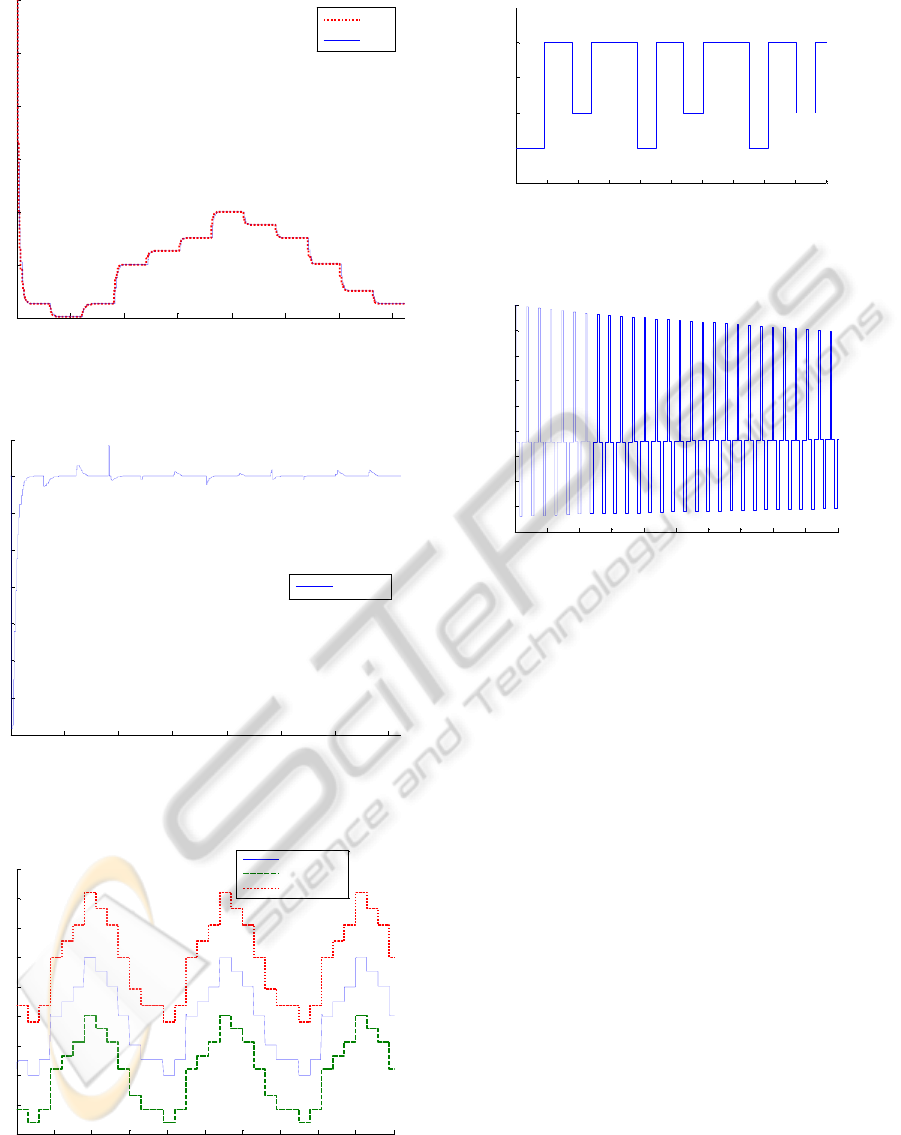
Figure 1: Evolution of the population size and the
reference sequence activated by the supervisor.
Figure 2: Evolution of the tracking error.
Figure 3: Evolution of the control sequence (inverse of the
environment carrying capacity).
Figure 4: Estimation algorithm/reference model pair
activated by the supervisor.
Figure 5: Evolution of the estimated of the active
algorithm.
to local modifications around nominal values of the
carrying capacity. Figure 4 displays the estimation
algorithm which is online activated by the supervisor
during the simulation. The active algorithm is
changed by the supervisor several times during a
year, which is reasonable due to the periodic
fluctuations in the species intrinsic growth rate.
Figure 5 displays the time evolution of the estimated
of the unknown parameter corresponding to the
active estimation algorithm.
Finally, the performance indexes given by
()
k
2
(i) *(i)
ij
j0
J(k) x x
=
=−
∑
j
0
k
∀
∈N
)
j
2
j
and , if an
adaptive control algorithm with a unique estimation
algorithm (without supervisor) is used, or given by
if the multi-estimation
scheme is used, are considered in order to compare
the tracking performance of the developed multi-
estimation scheme with the tracking results obtained
with any of the single estimations algorithms
working alone. Both indexes are measures of the
tracking error accumulated during the simulation.
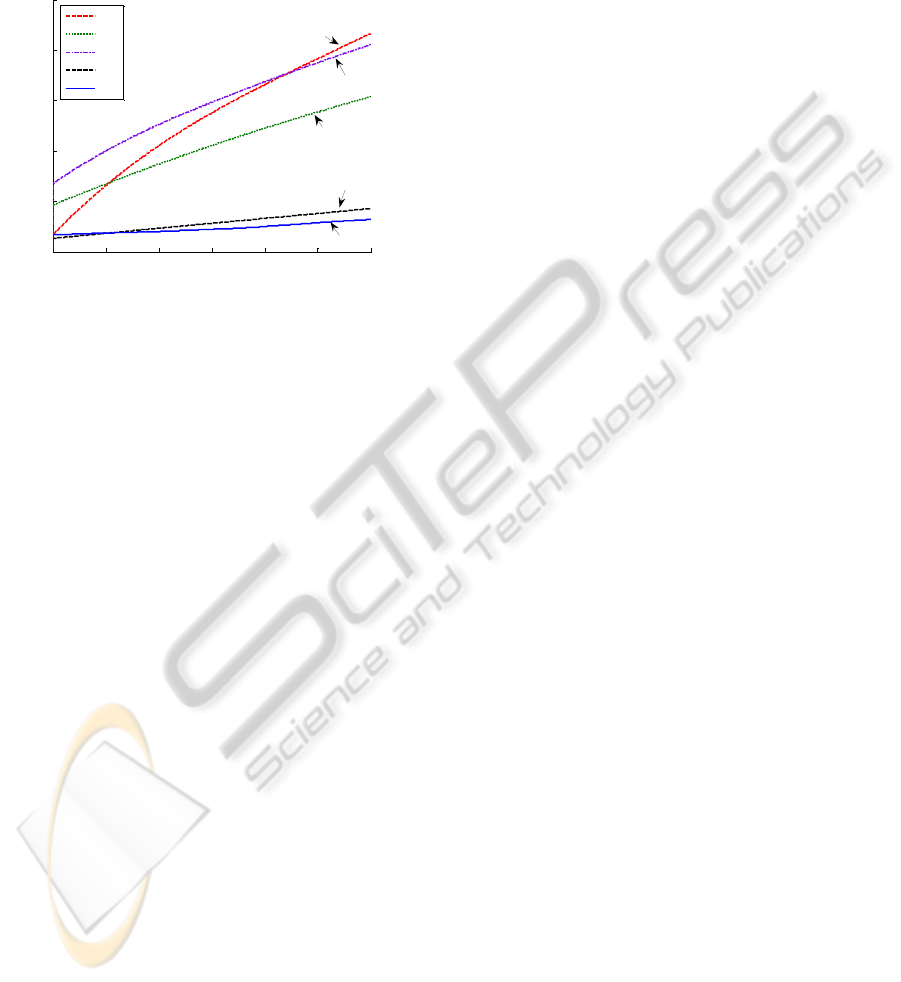
Figure 6 below displays the performance indexes
corresponding to the four simulations with the single
e
iS∀∈
(
j
k
(c ) *(c )
mj
j0
J(k) x x
=
=−
∑
0 50 100 150 200 250 300 350
180
200
220
240
260
280
300
kT
x
m
(k)
xk
0 50 100 150 200 250 300 350
-7
-6
-5
-4
-3
-2
-1
0
1
kT
x(k)-x
m
(k)
0 100 200 300 400 500 600 700 800 900 1000
160
170
180
190
200
210
220
230
240
250
kT
K(k)
lower bound
upper bound
0 100 200 300 400 500 600 700 800 900 1000
1
2
3
4
kT
actived estimation algorithm
0 1000 2000 3000 4000 5000 6000 7000 8000 9000 10000
0.48
0.5
0.52
0.54
0.56
0.58
0.6
0.62
0.64
0.66
kT
active estimated of a
A MULTI-ESTIMATION SCHEME FOR CONTROLLING THE BEVERTON-HOLT EQUATION IN ECOLOGY
139

ACKNOWLEDGEMENTS
estimation algorithms and the simulation with the
multi-estimation scheme incorporating the
supervisor. Note that the best behaviour is obtained
with the multi-estimation scheme, what motivates
the use of the adaptive control strategy developed in
this paper.
The authors are very grateful to MCYT by its
support through grants DPI2006-00714 and
DPI2009-07197.
0 0.5 1 1.5 2 2.5 3
x 10
4
0
500
1000
1500
2000
2500
kT
J
1
(k)
J
2
(k)
J
3
(k)
J
4
(k)
J
m
(k)
J
1
(k)
J
2
(k)
J
3
(k)
J
4
(k)
J
m
(k)
REFERENCES
Barrowman, N.J., Myers, R.A., Hilborn, R., Kehler, D.G.,
Field, C.A., 2003. The variability among populations
of coho salmon in the maximum productive rate and
depensation. Ecological Applications 13, pp. 784-793.
Beverton, R.J.H., Holt, S.J., 1957. On the dynamics of
exploited fish populations. Fish. Invest. 19, p. 1.
De la Sen, M., Alonso-Quesada, S., 2006. Adaptive
control of time-invariant systems with discrete delays
subject to multiestimation. Discrete Dynamics in
Nature and Society 2006, Article ID 41973, 27 pages,
doi: 10.1155/DDNS/2006/41973.
De la Sen, M., Alonso-Quesada, S., 2008. A control theory
point of view on Beverton-Holt equation in population
dynamics and some of its generalizations. Applied
Mathematics and Computation 199, pp. 464-481.
Figure 6: Tracking performances indexes.
5 CONCLUSIONS
De la Sen, M., Alonso-Quesada, S., 2009. Control issues
for the Beverton-Holt equation in ecology by locally
monitoring the environment carrying capacity: Non-
adaptive and adaptive cases. Applied Mathematics and
Computation 215, pp. 464-481.
BHE models are commonly used in Ecology to
describe the time evolution of species populations
in their habitats. Actually these models are subject
to parametrical uncertainties what motivates the use
of adaptive control techniques for such a purpose.
The design of an adaptive control system with a
multi-estimation scheme to achieve the solution of
the BHE tracks a desired reference signal has been
developed. The proposed use of a multi-estimation
scheme instead of a single estimation one is due to
two reasons, mainly. On one hand, Ecology systems
are usually time-varying in the sense that their
parameters suffer periodic fluctuations. On the other
hand, the signal used as control is the inverse of the
carrying capacity sequence, which depends on the
habitat characteristics. Then, locally modifications
of such a sequence around their nominal values are
only available to control the BHE solution. This
constraint makes that a suitable tracking
performance is only guaranteed if the BHE and the
reference model are locally deviated from each
other. Then, a set of potential reference models,
each one associated to an estimation algorithm,
instead of a unique one improves the tracking
behavior as it has been illustrated by some
simulation results.
Elsayed, E. M., Iricanin, B. D., 2009. On a max-type and a
min-type difference equation. Applied Mathematics
and Computation 215, pp. 608-614.
Feng, G., 1999. Analysis of a new algorithm for
continuous-time robust adaptive control. IEEE
Transactions on Automatic Control 44, pp. 1764-1768.
Iricanin, B. D., Stevic, S., 2009. Eventually constant
solutions of a rational difference equation. Applied
Mathematics and Computation 215, pp. 854-856.
Iricanin, B. D., Stevic, S., 2009. On some rational
difference equations. Ars Combinatoria 92, pp. 67-72.
Narendra, K. S., Balakrishnan, J., 1997. Adaptive control
using multiple models. IEEE Transactions on
Automatic Control 42, pp. 171-187.
Stevic, S., 2006. A short proof of the Cushing-Henson
conjecture. Discrete Dynamics in Nature and Society
2006, Article ID 37264, 5 pages, doi:
10.1155/DDNS/2006/37264.
Stevic, S., 2010. On a generalized max-type difference
equation from automatic control theory. Nonlinear
Analysis – Theory, Methods and Applications 72, pp.
1841-1849.
Future research will extend these adaptive
control techniques to other Ecological systems as,
for example, epidemic propagation models.
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
140