FDI WITH NEURAL AND NEUROFUZZY APPROACHES

Application to Damadics

Y. Kourd, N. Guersi

Department of Control Engineering, Faculty of Science and Engineer, Mohamed Khider Biskra University, Algeria

Department d'Electronique, Université Badji Mokhtar Annaba, Algeria

D. Lefebvre

GREAH – Université Le Havre, 25 rue Philippe Lebon, 76058 Le Havre, France

Keywords: Fault Diagnosis, Modelling, Residual Generation, Residual Evaluation, Neural Classifier, Neurofuzzy

Classifiers.

Abstract: Fault diagnosis is a major challenge for complex systems as long as it increases the safety and

productivity. This work concerns faults diagnosis, based on artificial intelligence, neural networks, and

fuzzy logic. Thanks to an associative memory, neural networks have good capacities of organization,

approximation and classification. Combined with fuzzy logic, neural networks are an effective tool for

system modelling, fault detection and fault diagnosis. This paper illustrates the potential of these tools for

the modelling and the diagnosis of an industrial actuator (DAMADICS benchmark).

1 INTRODUCTION

Fault detection and isolation (FDI) is a major issue

for complex systems as long as it increases the

safety and productivity of these systems. Its first

vocation is the detection and the isolation of system

failures. The necessity to detect and isolate early the

failures calls upon techniques of the artificial

intelligence. These techniques have been recently

developed and improved by many researchers. The

point is that artificial intelligence makes easier the

task carried out by the operators as long as the

observation of symptoms and the data analysis or

information interpretation is carried out by the

diagnosis system.

Several methods exist for the diagnosis of

dynamical systems. Basically, model-based and

data-based methods can be distinguished (Chow,

1980; Patton et al. 1989; Gertler, 1991; Willsky,

1976). Model – based methods compare the

measured data with the knowledge provided by the

model of theconsidered system in order to detect and

isolate the faults that disturb the process. Such

techniques require a sufficiently accurate

mathematical model of the process.Data-based

methods require a lot of process measurements and

can be divided into signal processing methods and

artificial intelligence approaches. Model and data

based methods are used to design residual signals.

The fault detection results from the comparison of

the residuals with arbitrary thresholds: a fault is

detected each time one residual ccross over the

threshold. This comparison is calculated on line. To

isolate the faults, residuals are structured to be

robust and sensitive to some specific sets of faults.

In this context, our study concerns the

investigation of model-based FDI methods with

artificial intelligence, particularly neural networks

and fuzzy logic. Fuzzy logic can be used to describe

the system behaviours according to linguistic rules

and fuzzy sets. The advantage of fuzzy logic is that

it can be used in presence of uncertainties. The

drawback is that the number and expression of the

rules and also the parameters of the membership

functions that define the sets are not easy to be work

out. In that case, neural networks are helpful to

identify the unknown parameters according to

measured data and to learning algorithms.

This paper concerns the application of neural

networks, fuzzy logic and neurofuzzy systems

(ANFIS) for an industrial actuator from the sugar

factory in Lublin, Polen (Damadics, 2004).

368

Kourd Y., Guersi N. and Lefebvre D. (2010).

FDI WITH NEURAL AND NEUROFUZZY APPROACHES - Application to Damadics.

In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 368-372

DOI: 10.5220/0002928103680372

 SciTePress

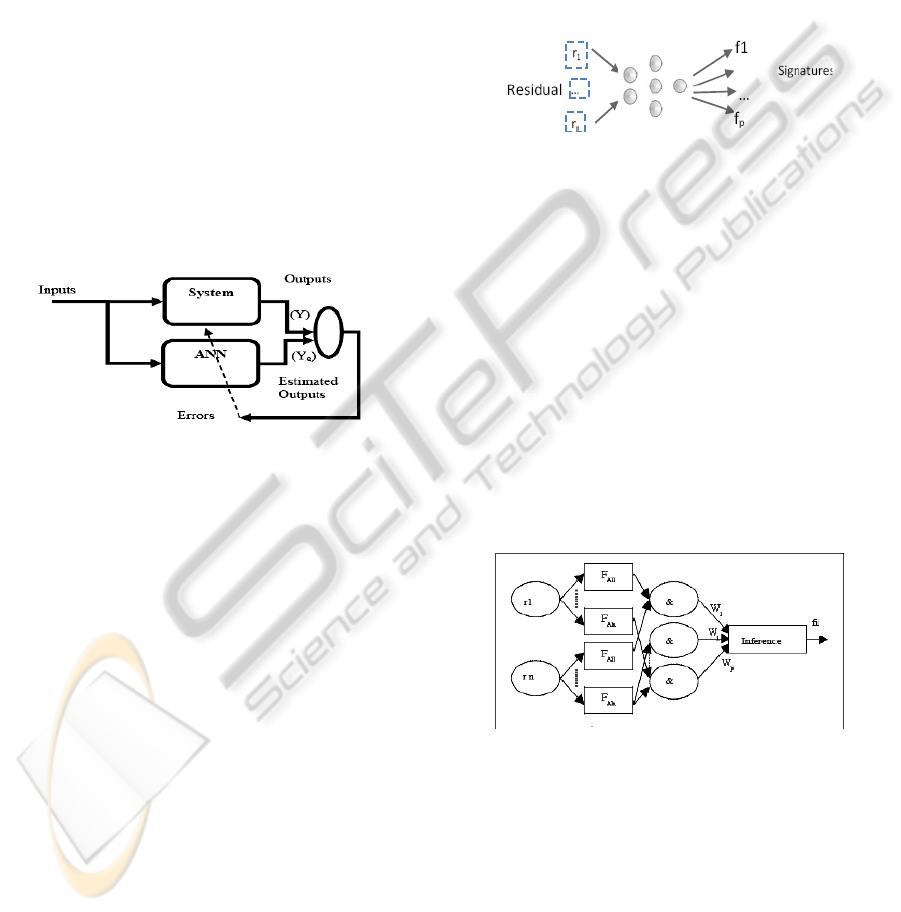
2 FDI METHODS

The proposed approach can be presented with 3

stages (1) the design of a data – based model; (2) the

fault detection according to a residual generator; (3)

the fault isolation thanks to neural or neurofuzzy

classifiers.

2.1 Reference Model Design

In the following we consider dynamic systems with

q inputs u

(t) and n outputs y

(t) and it is assumed

that the state variables are no measurable. Such

systems exhibit often complex dynamics, with

strong nonlinearities. As a consequence, knowledge

–based models are not easy to obtain. Another

approach lies in the data–based models. Artificial

neural networks (ANN) are often used for that

purpose (Juditsky et al. 1995). The goal is to design

a model that will be used for the generation of

residuals (figure 1).

Figure 1: Data-based model design.

In order to get the best ANN architecture, several

configurations are tested according to a trial – error

processing that uses pruning to eliminate the useless

nodes. The learning of the ANN is obtained

according to the Levenberg-Marquardt algorithm

with early stopping. This algorithm is known for its

rapid convergence. During learning stage, the ANN

is trained with data collected during the normal

functioning of the system. Then the ANN reference

model is validated with another set of data.

2.2 Fault Detection

The considered system may be affected by p faults

Fi with the assumption that simultaneous faults do

not occur. The vector r(t) of n residuals r

(t) is

calculated according to the difference between the

outputs vector of the system y(t) and the output

vector of the ANN model y

(t). As long as the

system has no fault, the estimated output y

(t)

remains in the neighbourhood of the actual output

y(t) and the residual r(t) is near zero. When a fault

occurs, at least one estimated output becomes

different from and the actual one and the

corresponding residual is no longer near zero.

2.3 Fault Isolation with ANN

A neural classifier has been developed to isolate the

faults after detection (Kourd et al., 2008). This

classifier is a multilayer Perceptron ANN (figure 2).

The inputs are the n residuals r

(t) and the outputs

are the p signatures f

of the faults F

that are under

consideration.

Figure 2: Neural classifier.

The neural classifier is trained and validated with

a learning algorithm similar to the one used for

reference model design.

2.4 Fault Isolation with ANFIS

In order to deal with improve the isolation, a

neurofuzzy classifier has also been developed

(figure 3). Such a classifier has an hybrid

architecture that takes advantages from fuzzy logic

and neural networks (Nauck et al. 1995). This

classifier is design as a double Takagi- Sugeno

ANFIS networks. The inputs are the n residuals r

(t)

and the outputs are the p signatures f

of the faults F

that are under consideration.

Figure 3: Double neurofuzzy ANFIS classifiers.

3 APPLICATION TO DAMADICS

3.1 System Description

The system under consideration is the DAMADICS

valve (figure 4). It is composed of a pneumatic

servomotor and a controller that drives the valve.

FDI WITH NEURAL AND NEUROFUZZY APPROACHES - Application to Damadics

369

Figure 4: Actuator shema.

This system has four input variables (CV, P1, P2,

T1) and 2 outputs variables (X, F) that are described

in table 1 (DAMADICS 2004). The other variables

are not considered in our application.

Table 1: Input and output variables.

There exist 20 possible faults that may affect the

functioning of the actuator (DAMADICS 2004).

Some faults may be abrupt or incipient ones.

3.2 Model Design

The actuator is modeled with two multilayer

perceptrons ANN that represent the interaction

between the inputs and the outputs according to (1):

netX = netX (CV, P1, P2, T1)

(1)

netF = netF(X, P1, P2, T1)

To select the structure of the neural networks

netX and netF, numerous tests have been carried out

to obtain the best architectures (i.e. number of

hidden layers and number of neurons by layer) in

order to model the operation of the actuator. The

training and test data were generated by the

simulation of the Matlab-Simulink actuator model

(Kourd et al. 2008).

From table 2, we notice that netX(6,3,1) and

netF(6,3,1) give the best results. When the training is

over, the ANN netF provides estimated outputs that

are not far from the actual ones. Validation is done

with the measured data provided by the ‘Lublin

Sugar Factory in 2001 (DAMADICS, 2004).

Validation is illustrated on figure 5.

Table 2: netX and netF neural networks structure.

Figure 5: Actual output F and estimated output netF (up);

Instantaneous error (down).

The modelling error is acceptable. Similar

conclusions are obtained with ANN netX. Let notice

that the output of netX is an input for netF and the

sensitivity of the estimation depends strongly on the

error on netX. As a conclusion, both ANNs provide

a good approximation of the actuator dynamics.

3.3 Fault Detection

In the following four faults will be considered: F7

(medium cavity or critical flow) F10 (servo-motor's

diaphragm perforation) F15 (positioner spring fault)

and F17 (positioner supply pressure drop) in order to

illustrate the efficiency of the proposed approach.

Two residual are designed according to (2):

rF = F - netF

(2)

rX = X - netX

During normal functioning the residuals remain

near zero: their magnitude is in range [-0,2; 0,2].

The value 0.2 will be used as detection threshold

(Emami-Naeini, 1988; Ding and Frank, 1991). Let

us notice that a low pass filter is used to remove high

frequency noises. In figure 6, the residuals are

worked out when the fault F7 is simulated during

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

370

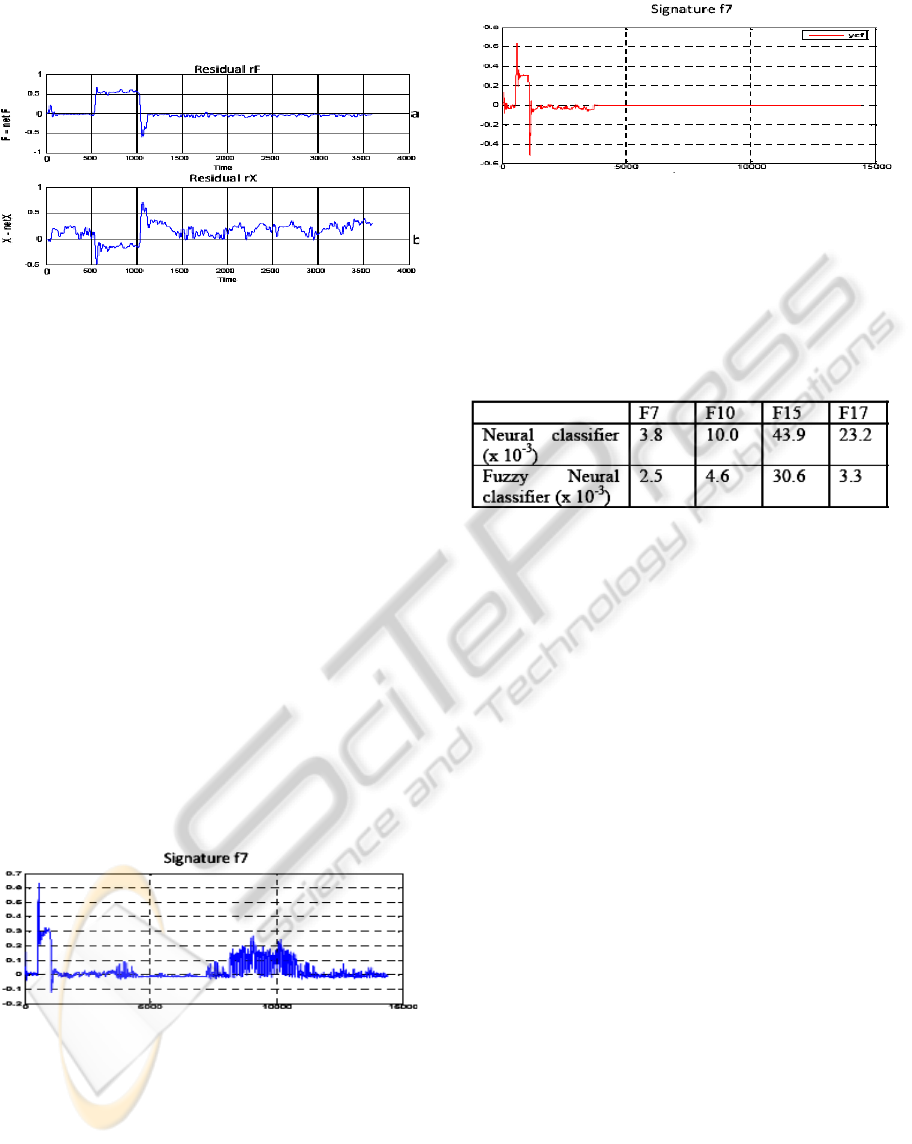
interval [500 1000] time units (times units are in

seconds).



Figure 6: Residual in presence of fault F7; Residual rF

(up); Residual rX (down).

3.4 Fault Isolation

The classifiers presented in section 2 are trained

with a set of simulated faults. Then they are

validated according to the real data collected on the

Sugar factory:

During period [500, 1100], the fault F7 occurs.

During period [4100, 4600], the fault F10 occurs.

During period [7700, 9000], the fault F15 occurs.

At times 11300 and 11850 the fault F17 occurs.

The ANN classifier presented in section 2.3

receives two inputs: the residuals rX and rF and

delivers four outputs that are the signatures f7, f10,

f15, f17 of the faults F7, F10, F15, F17. The

signature f7 is given in figure 7. The neural classifier

gives acceptable results in the sense that the

signature of each fault is far from zero when the

considered faults occur. But misclassifications may

occur.





Figure 7: Magnitude of the fault signatures f7 in function

of time for ANN classifier.

The ANFIS classifier presented in section 2.4 has

also two inputs and four outputs. The resulting

signature f7 is given in figure 8.

Figure 8: Magnitude of the fault signature f7 in function of

time for ANFIS classifier.

The use of ANFIS classifier improves the

classification results. The number of

misclassifications decreases and the quadratic mean

square on error of the residuals decreases (table 3).

Table 3: Quadratic mean square error.

4 CONCLUSIONS

This paper uses neural networks and fuzzy logic for

the fault diagnosis. The neural networks are good

tools for the modelling and diagnosis of non linear

processes, but some problems remain in the

selection of the optimal architecture as well as the

number of layers, and the numbers of neurons in

each layer. The uses of neurofuzzy networks

improve the classification of faults.

In our further works we will consider numerical

criteria to compare both classifiers, we will also

compare our results with the existing results and we

will improve the neurofuzzy diagnosis system.

REFERENCES

Chow, E. Y., Failure detection system design

methodology, Thesis, Lab. Information and Decision

system, M.I.T, Cambridge, 1980.

Ding, X., Frank P. M., Frequency domain approach and

threshold selector for robust model-base fault

detection and isolation, Proc. SAFEPROCESS'91,

Baden-Baden, Germany, vol. 1, pp. 307-312, 1991.

Emami-Naeini, A. E. A., Effect of model uncertainty of

failure detection: the threshold selector, IEEE-TAC,

33, pp. 1106- 1115, 1988.

Gertler, J. J., Analytical redundancy methods in fault

detection and isolation – survey and synthesis, Proc.

FDI WITH NEURAL AND NEUROFUZZY APPROACHES - Application to Damadics

371

SAFEPROCESS’91, Baden-Baden, Germany, pp. 9-

21, 1991.

Juditsky, A., Hjalmärsson, H., Benveniste, A., Delyon, B.,

Ljung, L., Sjöberg, J., Zhang, Q., Nonlinear black-box

modelling in system identification: mathematical

foundations. Automatica, 31, pp. 1725-1750, 1995.

Nauck, D., Kruse, R., Nefclass – A neurofuzzy approach

for the classification of data, Proc. Symp. on Applied

Computing – ACM, Nashville, USA, 1995.

Patton, R. J., Frank, P. M., Clarck, R. N., Fault diagnosis

in dynamic systems, Prentice Hall, 1989.

Willsky, A. S., A survey of design methods for failure

detection in dynamic systems, Automatica 12, pp.

601-611, 1976.

Kourd, Y., Guersi, N., Lefebvre, D., A two stages

diagnosis method with neuronal networks, Proc.

ICEETD 2008, Hammamet, Tunisie.

DAMADICS (2004): Website of DAMADICS:

Development and Application of Methods for

Actuator Diagnosis in Industrial Control Systems.

http://diag.mchtr.pw.edu.pl/damadics/.

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

372