A ROBUST MOSAICING METHOD FOR ROBOTIC ASSISTED

MINIMALLY INVASIVE SURGERY

Mingxing Hu, David J. Hawkes

Centre for Medical Image Computing, University College London, London, U.K.

Graeme P. Penney

Department of Imaging Sciences, King’s College London, U.K.

Daniel Rueckert, Philip J. Edwards, Fernando Bello, Michael Figl

Department of Computing, Imperial College, London, U.K.

Roberto Casula

Cardiothoracic Surgery, St. Mary’s Hospital, London, U.K.

Keywords: Video Mosaicing, Robotic Assisted Minimally Invasive Surgery, Homography, Trifocal Tensor, Bundle

Adjustment.

Abstract: Constructing a mosaicing image with broader field-of-view has become an interesting topic in image guided

diagnosis and treatment. In this paper, we present a robust method for video mosaicing in order to provide

more guiding information for robotic assisted minimally invasive surgery. Outliers involved in the feature

dataset are removed using trifocal constraints, homographies between images are estimated with



L -norm

optimization and chained together in a practical way. Finally refinement based on bundle adjustment is

applied to minimize the error between reprojection and feature measurement. The proposed method has

been tested with endoscopic images from Totally Endoscopic Coronary Artery Bypass (TECAB) surgery.

The results showed our method performs better than other typical methods in terms of accuracy and

robustness to deformation.

1 INTRODUCTION

The past decade has witnessed significant advances

on robotic assisted Minimally Invasive Surgery

(MIS) evolving from early laboratory experiments to

an indispensable tool for many surgeries. MIS offers

great benefits to patients: the incisions and trauma

are reduced and hospitalisation time is shorter.

Robotic assisted techniques further enhance the

manual dexterity of the surgeon and enable him to

concentrate on the surgical procedure. Despite of all

these advantages, MIS using an endoscope still

suffers from a fundamental problem: the narrow

field-of-view. As a result, the restricted vision

impedes the surgeon’s ability to collect visual

information from the scenes and his/her awareness

of peripheral sites.

A straightforward solution to overcome the

difficulty is video mosaicing, creating a 2D image

with wider field-of-view by aligning and properly

blending a number of partly overlapped images

acquired at different positions. A lot of research

work about video mosaicing has been done in both

computer vision and medical imaging communities.

1n 1975, Milgram (Milgram, 1975) proposed the

first photomosaics method by minimizing the visual

impact of the introduced seam. Geometric and

greyscale information was used to combine the

images on a line-by-line basis and to choose a best

seam point for each line. After that, this area has

attracted great attention from researchers in

206

Hu M., Hawkes D., Penney G., Rueckert D., Edwards P., Bello F., Figl M. and Casula R. (2010).

A ROBUST MOSAICING METHOD FOR ROBOTIC ASSISTED MINIMALLY INVASIVE SURGERY.

In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 206-211

DOI: 10.5220/0002928902060211

 SciTePress

computer vision community. For example, Zoghlami

et al. (Zoghlami et al., 1997) proposed a

feature-based algorithm to compute the homography

between images with relatively small overlap and

experimental results showed that it could deal with

large rotation around optical axis and zooming factor.

Alternatively, Capel (Capel, 2001) focused on the

global registration for the video mosaicing, the

alignment of the image frames, taking into account

all the overlapped images, and not just the

consecutive ones. Maximum likelihood estimate was

used to build the chain of consisted homographies

using all the available feature points. Most recently,

Brown and Lowe (Brown and Lowe, 2007)

introduced an automatic mosaicing method based on

the invariance features. The features are detected

and matched together between images using SIFT

(Lowe, 2004). This method is robust to orientation,

scale and illumination of the input images and can

recognize multiple panoramas in an unordered

image dataset. These methods work well for static

scene without any deformable objects in it. However,

medical image usually involves some deformation

from organs and soft tissues, which often lead to the

failure of these methods.

In medical imaging community, Seshamani et al.

(Seshamani et al., 2006) presented an endoscopic

mosaicing technique to display a wider field-of-view

of the surgical scene by stitching together images.

This method, which was evaluated using

microscopic retinal and catadioptric endometrial

images, can perform online image registration and

provide warping models to handle tubular organ

structure. Vercauteren et al. (Vercauteren et al., 2006)

also proposed a similar mosaicing method but they

applied statistics for Riemannian manifolds to

pairwise registration. Their method is able to

produce a globally consistent mapping of input

frames which is also aligned to a reference plane. It

also considers non-rigid deformations of soft tissue,

and the irregular sampling present in fibered

confocal microscopy. Recently Miranda-Luna et al.

(Miranda-Luna et al., 2008) also proposed a method

of mosaicing of bladder endoscopic images by

mutual information-based similarity measure and

stochastic gradient optimization. Besides, an

undistortion method is used to preprocess the

endoscopic images in order to improve the

robustness of the registration. Unfortunately, a

common trait shared by these methods is the

requirement of large overlap to guarantee the

convergence and accuracy of the local and global

alignment.

So in this paper, we propose a robust method to

mosaic medical images for robotic assisted

minimally invasive surgery. Good features are

detected and tracked based on the optical flow and

then the potential outliers are removed from the

feature dataset using the trifocal tensor.

Homographies between images are estimated using

Second-Order Cone Programming (SOCP) under



-norm. Then they are chained together under a

common and global reference system, followed by

bundle adjustment refinement to minimize the total

misalignment. The contributions of the proposed

method are as follows: (1) Mosaicing image with a

broader field-of-view can be constructed from the

input images containing deformable organs and soft

tissues. Thus it can be used for 2D-3D registration of

the anatomy to the preoperative CT/MRI data in

order to provide more information for image guided

diagnosis or surgery. (2) A robust strategy based on

the trifocal tensor and bundle adjustment is used to

remove outliers obtained from incorrect locations

and incorrect tracking and to obtain the global

alignment by minimizing the reprojection error.

2 ROBUST ESTIMATION FOR

VIDEO MOSAICING

Given a set of images

( mi , ,1  ), and some

image point





yx 1 , ,x detected on each frame

. If two images

and

can be related by a

linear transformation of the projective plane, we

have

jjii

xHx



(1)

where

H is a 33



matrix, representing the

2D-2D transformation via a projective plane, also

called a homography.

2.1 Feature Detection and Tracking

The first step to construct mosaicing image is to

track image features as the camera moves. One of

the well-known tracking methods is the

Lucas-Kanade (LK) tracker (Tomasi and Kanade,

1992). The LK tracker minimizes the sum of squared

errors between two images

and

1k

altering the warping parameters

p which are used

to warp

1k

to the coordinate frame of

. For a

general motion model with transformation function





px ,W , the objective function is



















xppx

;min

IWI

(2)

A ROBUST MOSAICING METHOD FOR ROBOTIC ASSISTED MINIMALLY INVASIVE SURGERY

207

This expression is linearized by a first order

Taylor expansion on







ppx 



;

 























;min

kkk

IWI

(3)

Where

1



I is the image gradient vector and

pW is the Jacobian of the transformation

function.

2.2 Outlier Removal

Usually there are some outliers in the feature dataset

after the detection and tracking, and they are in gross

disagreement with a specific postulated model and

must be handled by robust approaches. More

importantly, the



L optimization, which will be

discussed in the next section, is very vulnerable to

outliers. So the outlier removal is crucial to the

success of the whole mosaicing process.

Given three cameras characterized by projective

matrices





0IP  , ][ VAP







, ][ VBP







, the

images of a 3D point in each view can be denoted as



yx 1 , ,x ,



yx 1 , ,







x ,



yx 1 , ,







x in

homogeneous coordinates. It can be noted that

matrices

A and B are 2D homograph matrices,

where Axx 



and Bxx 



, and V



and V



are

the projection of the first camera centre into the

second and third images. Then the trilinear

constraints across the three views can be compactly

expressed in terms of trifocal tensor,

T , which is a

333  matrix with 27 entries. And the relation

xxx







 can be described as (Shashua, 1995)

jjk

avbvT







 , 3 ,2 ,1 , , kji

(4)

Since every corresponding triplet

x ,



contributes four linearly independent equations, then

seven point correspondences uniquely determine (up

to scale) the tensor

. In fact the trifocal tensor can

be estimated from a minimum of six point

correspondences since it has only 18 degrees of

freedom. However, the six-point estimation involves

the solution of a cubic and a complicated

parameterization (Quan, 1994), and so for simplicity,

we use the seven-point method to compute a

possible solution and employ the RANSAC strategy

to detect the outliers based on the geometric error.















iiiiii

dddRR

222

x,xx,xx,x

(5)

This error measures the sum-of-squares of the

geometric distances between the image points

iii

xxx









and the corrected data points

iii

xxx

ˆˆˆ







 , with the latter obeying the trilinear

constraint Eq. (4) for the estimated tensor

. Thus,

given three images with overlap, we can estimate the

trifocal tensor among them and use the above error

measure to detect outliers accordingly.

The above method is only applicable to three

images, we require a method to process an entire

image sequence and remove the outliers. The

simplest way is to compute the tensor among three

consecutive images,





2 ,1 , 



iii , e.g., image triplet,





3 ,2 ,1 ,





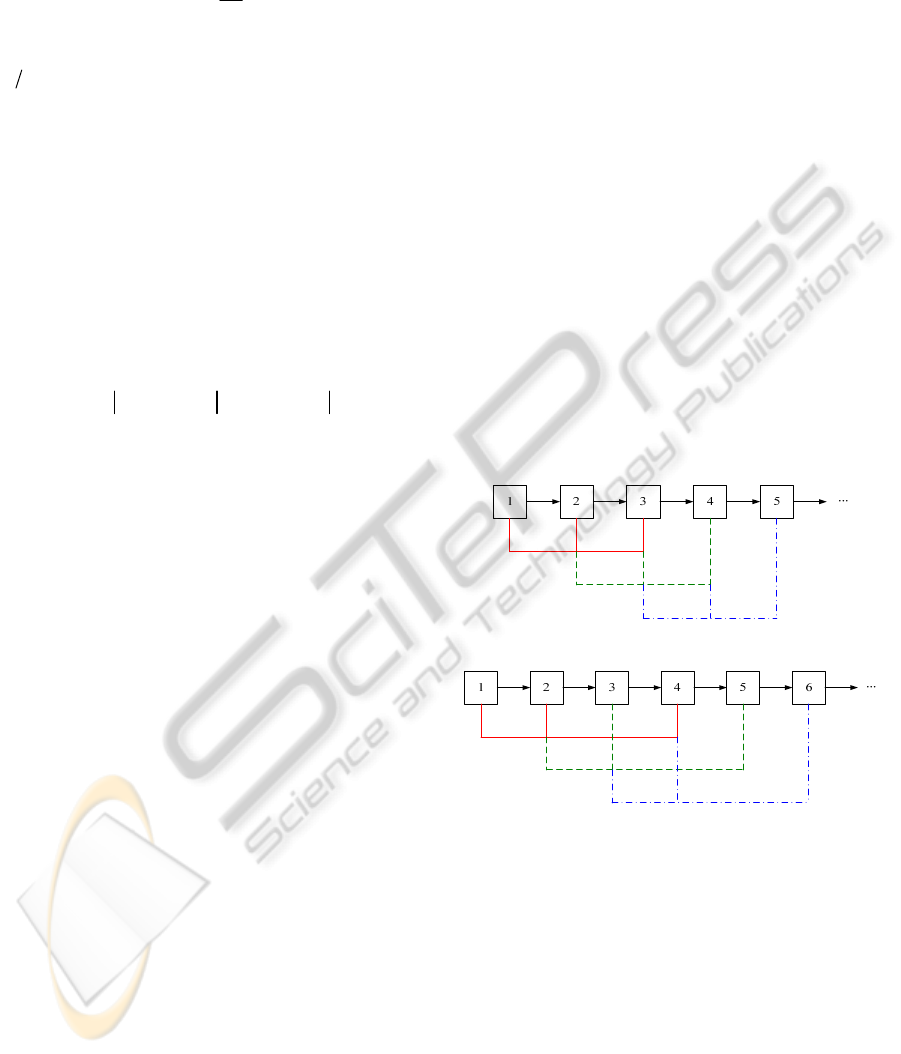
4 ,3 ,2 , etc, as shown in Fig.1 (a), and

delete feature points if they are considered an

outlier from any independent tensor estimation.

Besides, we also employ additional image triplets

for computation, e.g.,





3 ,1 ,  iii

, as shown in

Fig.1 (b). However, the more image triplets that are

used, the more feature points will be removed if a

previous decision rule is applied (e.g. once an outlier,

always an outlier). Our method carries out a number

of independent tests (each time using a unique

combination of three images) on each feature point.

Feature points are only removed if they are

determined to be outliers more than 50% of the

times.

3,2

4,3

5,4

(a)

4,2

5,3

6,4

(b)

Figure 1: Strategy of outlier removal based on trifocal

tensor. (a) The three consecutive images





2 ,1 ,



 iii

are used to compute the trifocal tensor. (b) More nearby

images





3 ,1 ,



iii are used to remove the outliers from

the image sequence.

2.3 Image Alignment

Today



-norm optimization has been widely used

in various multiple-view geometry problems (Kahl

and Hartley, 2008). One of the main advantages of



is that: problems formulated by



often

possess a single, hence global, optimum. Besides, it

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

208

usually leads to a simpler formulation for the same

problem compared with

Without loss of generality, we set the last

element of the homography

H ,

h , to 1 and have

hhh















3231

232221

131211

So the residual of homography estimation between

image

i and

can be expressed as





 



xhhxhh

ffyx

yxd













(6)

where

h represents the l -th row of the matrix

. So our aim is to solve the following optimization

problem by minimizing the residual







,min xx , s.t.



0s



Suppose each residual has an upper bound



, that

is,

 









kkkk





sss . Then the

formulation in (6) is equivalent to



 

min

s.t.

  

sss

kkkk



 , mk , ,1 





0s



Then we can use Second-Order Cone Programming

(Alizadeh and Goldfarb, 2003) to solve this problem.

Readers can refer to Kahl’s paper for more details

(Kahl and Hartley, 2008).

Ideally, after the alignment of all consecutive

images, we can chain all the images together and

wrap them onto a reference plane





















r i

iiir

iiirir

,11,

,11,,

Here image

is the reference frame. For simplicity,

it can be the middle image of the whole video

sequence.

However, the misalignment error usually

accumulates by concatenating homographies. This is

especially evident when the camera goes back to the

scene previously seen in a long image sequence. The

accumulation of error may be so great that the first

and last images are very poorly registered. In other

words, the homographies are not consistent with

alignment to a common frame. So we use a strategy

to minimize the number of good homographies to

link image

i with reference frame

(1) Find image

, which is the furthest to image

but with enough overlap. Here the overlap

can be the number of feature correspondences

between image

and

overlap





(2) Compute the homography between frame

and

i , and calculate the mean of the residual

error







D xx ,

(7)

(3) If

is small enough,

residualrj





, this

homography

rj ,

H is accepted. Then we start

from image



, and find the next

acceptable homography

rj ,

H using step (1)

and (2). If

residualrj





, we select the image

next to













jrj

if 1

and repeat (2) and (3).

(4) The process will halt until the whole

homography chain is built.

Thus, alignment can take advantage of

homographies linking non-consecutive frames and

reduces the global registration error.

2.4 Refinement based on Bundle

Adjustment

The bundle adjustment (BA, Triggs et al., 1999) we

used is different from the ones addressed in

McLauchlan’s (McLauchlan, and Jaenicke, 2002)

and Brown’s paper (Brown and Lowe, 2007). In

their papers, BA was used to solve the rotation

parameters and focal lengths of all cameras. In this

paper, BA was performed to find the best

homography set





ri,

H , mi , ,1 



, that minimize

the misalignment error.











rii

,,1

min



xHx

(8)

where

is the reprojecion of all the feature points

onto frame

. It can be easily computed using Least

Square method with all the available homographies.

Then Levenberg–Marquardt algorithm is used to sol-

A ROBUST MOSAICING METHOD FOR ROBOTIC ASSISTED MINIMALLY INVASIVE SURGERY

209

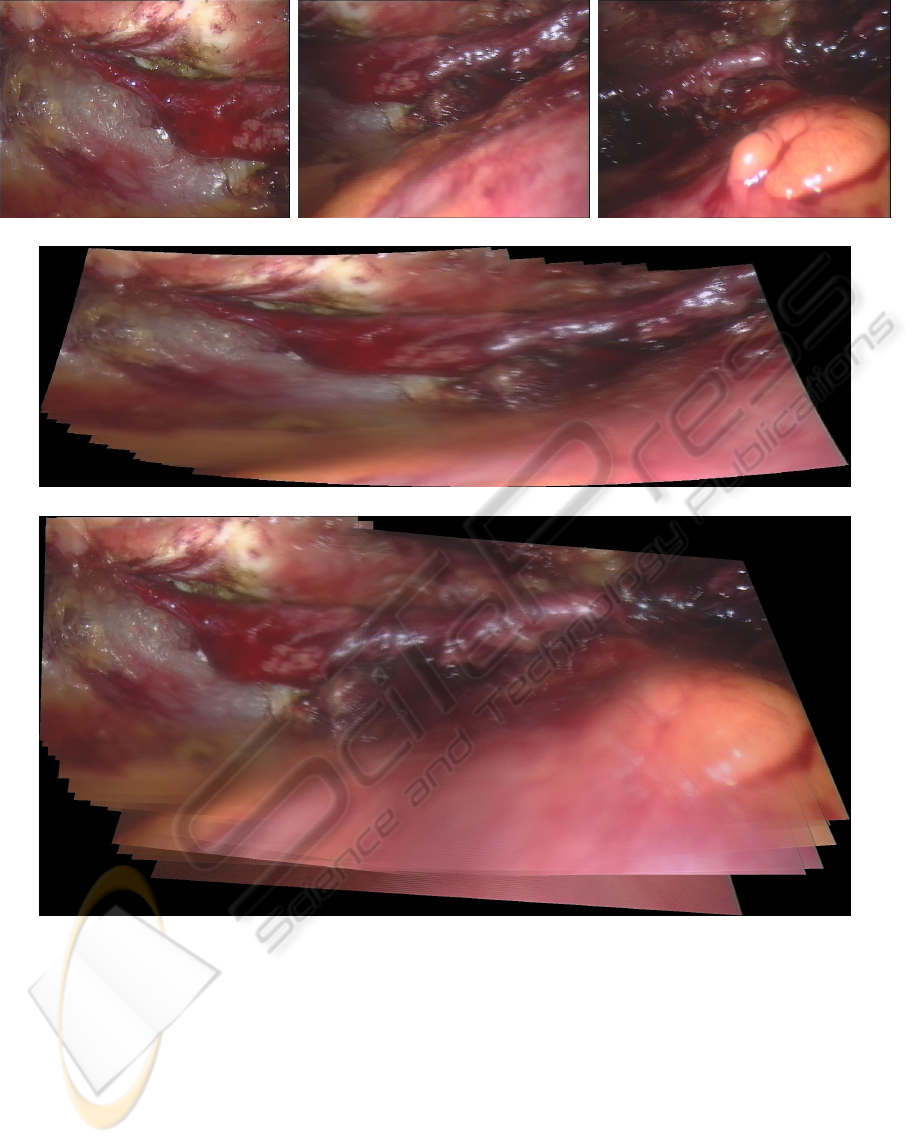
(a) (b) (c)

(d)

(e)

Figure 2: The experimental result of endoscopic images from Totally Endoscopic Coronary Artery Bypass surgery. (a), (b)

and (c) show the first, middle and last images of the sequence, respectively. (d) displays the mosaicing result of Brown’s

Method. (e) displays the mosaicing result of the proposed method.

ve Eq. (8). The C++ code about the generic sparse

bundle adjustment is available online by courtesy of

Manolis Lourakis.

3 EXPERIMENTAL RESULTS

In this section, the performance of the proposed

method was evaluated using endoscopic images

from Totally Endoscopic Coronary Artery Bypass

(TECAB) surgery and compared with Brown’s

method (Brown and Lowe, 2007).

The da Vinci

robotic surgical system (Intuitive

Surgical, Inc., Sunnyvale, CA, USA) was used to

obtain images of the heart surface. The video

endoscopic images were digitized at 25 frames per

second (fps) using a frame grabber (LFG4 PCI64,

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

210

Active Silicon, Uxbridge, U.K.). Although da Vinci

system provides stereo vision, we only use the image

sequence from left camera to perform the mosaicing

in order to compare with other methods. 150 images

were captured from the endoscope but we use only

30 frames (every 5 frame from the sequence) for the

mosaicing. Our aim is to create a mosaicing image

which includes the whole structure of the coronary

artery. The main challenge is the large complicated

non-rigid motion introduced by the beating heart

surface, which is shown in the right bottom of Fig. 2

(b) and (c).

Fig. 2 (d) displays the mosaicing result of the

proposed method. We can notice that the whole

vessel structure has been built correctly. So the

surgeon can realize the environment outside the

current scene when he views a part of the vessel.

More importantly, the mosaicing image can help him

link the endoscopic video with the preoperative

information from CT/MRI scan. Brown’s method

was also tested using this image sequence and the

mosaicing result was displayed in Fig. 2 (e). It is

noticed that only part (around three quarters) of the

whole vessel had been constructed and the images

affected badly by the beating heart surface could not

be used by Brown’s method. The possible reason is

that SIFT feature descriptor could not find enough

reliable features from the images with severe

deformation from the internal organ or soft tissue.

4 CONCLUSIONS

In this paper, we proposed a robust video mosaicing

method for robotic assisted minimally invasive

surgery. The mosaicing image displays a much wider

field-of-view of the operation scene and helps the

surgeon realize the surrounding environment outside

the current view. Experiments with TECAB

endoscopic images and FCM images show that the

proposed method performs better than other typical

methods. It is robust to deformation caused by

organs and soft tissues and can even deal with

artefacts involved in the images.

Effort in the near future will focus on future

improvement of robustness to deformation and

artefacts. Our long term goal is to automatically

construct mosaicing image of the surgical scene,

reconstruct the internal organ surfaces and register

these with the preoperative data (CT or MRI) to

provide more information for image guided

diagnosis and treatment.

REFERENCES

Alizadeh, F. and Goldfarb, D, 2003. Second-order cone

programming,

Mathematical Programming, 95 (1),

3-51.

Brown, M. and Lowe, D. G, 2007. Automatic Panoramic

Image Stitching using Invariant Features,

International Journal of Computer Vision, 74, 59–73.

Capel D. P. , 2001. Image Mosaicing and

Super-Resolution, Ph.D thesis, Dept. of Eng. Science,

Univ. of Oxford.

Kahl, F. and Hartley, R, 2008. Multiple-View Geometry

Under the Linfinity-Norm,

IEEE Trans. Pattern Anal.

Mach. Intell.

30(9): 1603-1617

Lowe, D. G., 2004: Distinctive Image Features from

Scale-Invariant Keypoints.

International Journal of

Computer Vision

, 60, 91–110.

McLauchlan, P. and Jaenicke, A, 2002. Image mosaicing

using sequential bundle adjustment.

Image and Vision

Computing

, 20(9–10):751–759.

Milgram D. L., 1975. Computer Methods for Creating

Photomosaics,

IEEE Trans. Computers, 24(11),

1113-1119.

Miranda-Luna, R., Daul, C., Blondel, W.C.P.M.,

Hernandez-Mier, Y., Wolf, D., Guillemin, F., 2008.

Mosaicing of Bladder Endoscopic Image Sequences:

Distortion Calibration and Registration Algorithm.

IEEE Trans. on Biomedical Engineering 55, 541–553.

Quan, L., 1994. Invariants of 6 points from 3 uncalibrated

images.

In: Proc. ECCV , 2, 459-470.

Shashua, A., 1995. Algebraic functions for recognition.

IEEE Trans. Pattern Analysis and Machine

Intelligence

, 17 (8), 779-789.

Seshamani, S., Lau W., and Hager, G., 2006. Real-Time

Endoscopic Mosaicking.

In: Proc. MICCAI, 355-363.

Tomasi, C., and Kanade, T., 1992. Shape and Motion from

Image Streams under Orthography: a Factorization

Method.

Int. J. Computer Vision, 9(2), 137-54.

Triggs, W., McLauchlan, P., Hartley, R., and Fitzgibbon,

A. 1999. Bundle adjustment: A modern synthesis.

Vision Algorithms: Theory and Practice

, number 1883

in LNCS. Springer-Verlag. Corfu, Greece, pp.

298–373.

Vercauteren, T., Perchant, A., Malandain, G., Pennec, X.,

Ayache, N., 2006. Robust mosaicing with correction

of motion distortions and tissue deformation for in

vivo fibered microscopy.

Medical Image Analysis, 10

(5), 673-692.

Zoghlami, I., Faugeras, O., and Deriche, R. 1997. Using

geometric corners to build a 2D mosaic from a set of

images. In Proc. CVPR, 420-425.

http://www.ics.forth.gr/~lourakis/sba/

A ROBUST MOSAICING METHOD FOR ROBOTIC ASSISTED MINIMALLY INVASIVE SURGERY

211