DATABASE AUTHENTICATION
BY DISTORTION FREE WATERMARKING
Sukriti Bhattacharya and Agostino Cortesi
Dipartimento di Informatica, Universita Ca’ Foscari di Venezia, Via Torino 155, 30170 Venezia, Italy
Keywords:
Database watermarking, ZAW, Public key watermark, Abstract interpretation.
Abstract:
In this paper we introduce a distortion free watermarking technique that strengthen the verification of integrity
of the relational databases by using a public zero distortion authentication mechanism based on the Abstract
Interpretation framework. The watermarking technique is partition based. The partitioning can be seen as a
virtual grouping, which does not change neither the value of the table’s elements nor their physical positions.
Instead of inserting the watermark directly to the database partition, we treat it as an abstract representation
of that concrete partition, such that any change in the concrete domain reflects in its abstract counterpart.
The main idea is to generate a gray scale image of the partition as a watermark of that partition, that serves
as tamper detection procedure, followed by employing a public zero distortion authentication mechanism to
verify the ownership.
1 INTRODUCTION
Because people pay much attention to data mining,
more and more research institutions begin to buy the
databases to analyze.The enterprises would also like
to sell their data warehouses for the institutions to do
their research if the data does not concern customers
personal data. The market of databases is flourishing
because this kind of demand and supply market is de-
veloped. But the database is easier to be copy and
abuse, and the internet is popular so that the informa-
tion propagates more rapidly. The information passes
through the internet without monitor and could be de-
stroyed or altered. The consumer of the information
would have no idea about the validity of the informa-
tion received.
Watermarking is a widely used technique to em-
bed additional but not visible information into the un-
derlying data with the aim of supporting tamper de-
tection, localization, ownership proof, and/or traitor
tracing purposes (Agrawal et al., 2003). Watermark-
ing techniques apply to various types of host con-
tent. Here, we concentrate on relational databases.
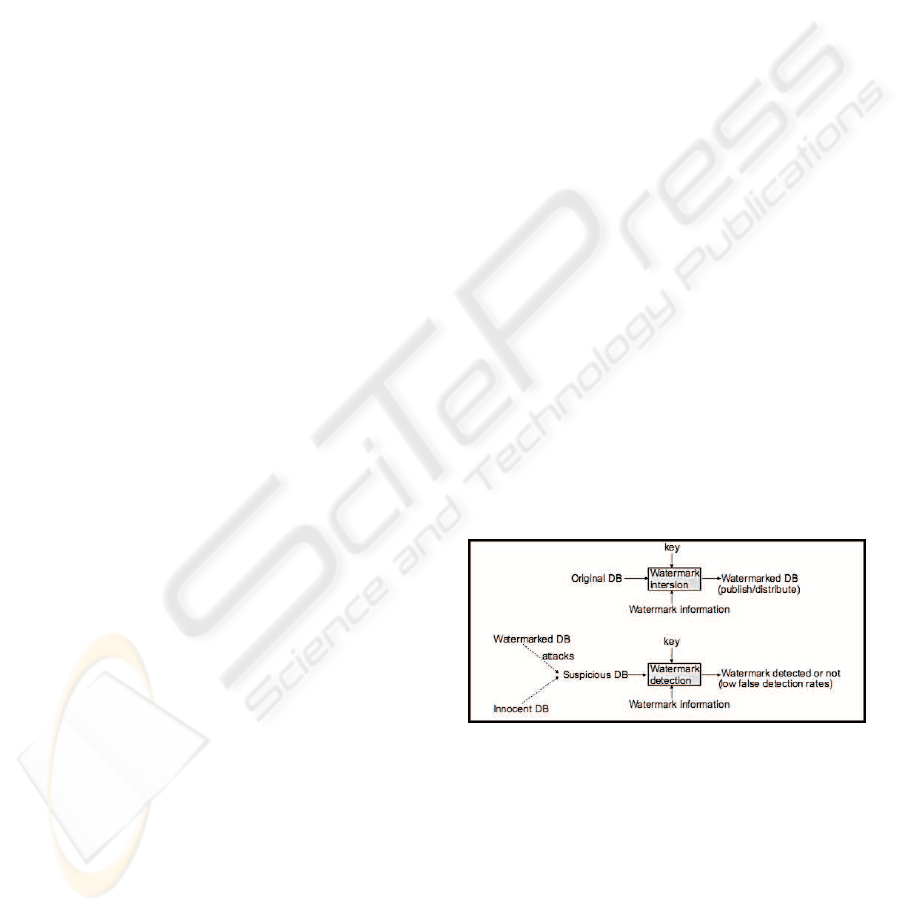
Database watermarking consists of two basic pro-
cesses: watermark insertion and watermark detection
(Agrawal et al., 2003), as illustrated in Figure 1. For
watermark insertion, a key is used to embed water-
mark information into an original database so as to
produce the watermarked database for publication or
distribution. Given appropriate key and watermark
information, a watermark detection process can be
applied to any suspicious database so as to deter-
mine whether or not a legitimate watermark can be
detected. A suspicious database can be any water-
marked database or innocent database, or a mixture
of them under various database attacks.
Figure 1: Basic watermarking process.
Watermarking has been extensively studied in the
context of multimedia data for the purpose of owner-
ship protection and authentication (Cox et al., 2001)
(Johnson et al., 2000). The increasing use of re-
lational database systems in many real life applica-
tions created an ever increasing need for watermark-
ing database systems. As a result, watermarking rela-
tional database systems is now merging as a research
area that deals with the legal issue of copyright pro-
tection of database systems.
The first well-known database watermarking
219
Bhattacharya S. and Cortesi A. (2010).
DATABASE AUTHENTICATION BY DISTORTION FREE WATERMARKING.
In Proceedings of the 5th International Conference on Software and Data Technologies, pages 219-226
DOI: 10.5220/0002929302190226
Copyright
c
 SciTePress

scheme for relational databases was proposed by
Agrawal and Kiernan (Agrawalet al., 2003) for water-
marking numerical values. The fundamental assump-
tion is that the watermarked database can tolerate a
small amount of errors. Since any bit change to a
categorical value may render the value meaningless,
Agrawal and Kiernan’s scheme cannot be directly ap-
plied to watermarking categorical data. To solve this
problem, Sion (Sion et al., 2004) proposed to wa-
termark a categorical attribute by changing some of
its values to other values of the attribute (e.g., ’red’
is changed to ’green’) if such change is tolerable in
certain applications. There have been other schemes
proposed for watermarking relational data. In Sion
et al.’s (Sion, 2004) scheme, an arbitrary bit is em-
bedded into a selected subset of numeric values by
changing the distribution of the values. The selection
of the values is based on a secret sorting. In another
work, Gross-Amblard (Gross-Amblard, 2003)designs
a query preserving scheme which guarantees that spe-
cial queries (called local queries) can be answered up
to an acceptable distortion.
All of the work cited so far (Agrawal et al.,
2003)(Gross-Amblard, 2003)(Sion et al., 2004)(Sion,
2004), assume that minor distortions caused to some
attribute data can be tolerated to some specified pre-
cision grade. However some applications in which
relational data are involved cannot tolerate any per-
manent distortions and data’s integrity needs to be
authenticated. To meet this requirement, we fur-
ther strengthen this approach and propose a dis-
tortion free watermarking algorithm for relational
databases and discuss it in abstract interpretation
framework proposed by Patrick Cousot and Rad-
hia Cousot (Cousot and Cousot, 1977) (Cousot and
Cousot, 1992) (Cousot, 2001) (Cousot and Cousot,
2004) (Cousot and Cousot, 2007).
In (Bhattacharya and Cortesi, 2009a) we pre-
sented a proposal in this direction, focusing on par-
titions based on categorical values present in the ta-
ble and generating a watermark as a permutations of
the ordering of the tuples.Then in (Bhattacharya and
Cortesi, 2009b) we faced the same issue by a more so-
phisticated and completely orthogonal approach that
allows us by removing the constraints on the presence
of categorical values in the table and by considering
any partitioning generate a binary image that serves
the purpose of temper detection of that associated par-
tition. Here, we go one step further. Namely we in-
troduce a distortion free watermarking technique that
strengthen the verificationof integrity of the relational
databases by using a public zero distortion authentica-
tion mechanism. Instead of binary image, we gener-
ate a gray scale image to strengthen the verification
of integrity and we employ a zero distortion public
authentication mechanism (Wu, 2003) for ownership
proof. We prove it as an abstract representation of
the actual partition by showing the existence of a Ga-
lois connection between the concrete and the abstract
partition (i.e. the gray scale image). Therefore, any
modification in the concrete partition will reflect in
the abstract counterpart. We state the soundness con-
dition regarding this alteration. The robustness of the
proposedwatermarking obviouslydepends on the size
of the individual groups so the overall architecture is
specifically designed for large databases. The result-
ing watermark is robust against various forms of ma-
licious attacks and updates to the data in the table.
Observe that our proposal improves both with re-
spect to our previous works on distortion free water-
marking and with respect to the application of hash
functions to the whole database: in fact the authen-
tication certificate we produce as a watermark does
not depend on the order of the tuples belonging to the
same partition set. This makes our approach scalable
to large databases while a simple hash function ap-
proach obviously does not scale well.
The paper is organized as follows. In section
2, we formalize the definition of tables in relational
database and the watermarking process. Section 3
illustrates how distortions and watermarking are re-
lated. In section 4, we present the data partitioning
algorithm and explain the partitioning in the abstract
interpretation framework. The watermark generation
algorithm for a data partition is illustrated in section
5. In section 6, we propose the watermark detection
algorithm. In section 7, we introduce a zero distortion
public authentication mechanism. The robustness of
the proposed technique is discussed in section 8. Fi-
nally we draw our conclusions in section 9.
2 PRELIMINARIES
This section contains an overview of Galois connec-
tion (Cousot and Cousot, 1977) (Cousot and Cousot,
1992) (Cousot and Cousot, 2007) and some formal
definitions (Haan and Koppelaars, 2007) and (Coll-
berg and Thomborson, 2002) of tables in relational
database and database watermarking.
Definition 2.1 (Partial Orders). A partial order on
a set D is a relation ⊑∈ ℘(D× D) with the following
properties:
• ∀d ∈ D : d ⊑ d (reflexivity)
• ∀d,d
′
∈ D : (d ⊑ d
′
) ∧ (d
′
⊑ d) =⇒ (d = d
′
) (an-
tisymmetry)
ICSOFT 2010 - 5th International Conference on Software and Data Technologies
220

• ∀d,d
′
,d
′′
∈ D : (d ⊑ d
′
) ∧ (d
′
⊑ d
′′
) =⇒ (d ⊑ d
′′
)
(transitivity)
A set with a partial order defined on it is called
partially ordered set, poset. Following are definitions
of some commonly used terms with respect to Partial
order (L, ⊑).
Definition 2.1.1 (Lower Bound). X ⊆ L has l ∈ L as
lower bound if ∀ l’ ∈ X : l ⊑ l’.
Definition 2.1.2 (Greatest Lower Bound). X ⊆ L
has l ∈ L as greatest lower bound l if l
0
⊑ l whenever
l
0
is another lower bound of X.It is represented by the
operator ⊓. glb(X)= ⊓ X.
Definition 2.1.3 (Upper Bound). X ⊆ L has l ∈ L as
upper bound if ∀ l’ ∈ X : l’ ⊑ l.
Definition 2.1.4 (Least Upper Bound). X ⊆ L has
l ∈ L as least upper bound l if l ⊑ l
0
whenever l
0
is another upper bound of X.It is represented by the
operator ⊔. lub(X)= ⊔ X.
Definition 2.2 (Complete Lattice). A complete lat-
tice (L, ⊑, ⊔, ⊓, ⊤, ⊥) is a partial ordered set (L, ⊑)
such that every subsets of L, has a least upper bound
as well as a greatest lower bound.
• The greatest element ⊤ = ⊓
/
0 = ⊔L
• The least element ⊥ = ⊓L = ⊔
/
0
For instance (L, ⊑, ⊔, ⊓, ⊤, ⊥) where L = {1, 2, 3,
4, 6, 9, 36}. ⊑ = |, ⊥= 1 and ⊤ = 36 is a complete
lattice. It can be represented using Hasse diagram as
shown below
Figure 2: Complete lattice.
Definition 2.3 (Galois Connection). Let C (con-
crete) and A (abstract) be two domains (or lattices).
Let α : C→ A and γ : A→C be an abstraction func-
tion and a concretization function, respectively. The
pair of functions (α,γ) form a Galois Connection if:
• both α and γ are monotone (order preserving).
• ∀ a ∈ A : α(γ(a)) ⊑ a
• ∀ c ∈ C : c ⊑ γ(α(c))
α and γ uniquely determine each other.
Definition 2.4 (Function). Let Π
i
be the projec-
tion function which selects the i-th coordinate of a
pair. F is a function over the set A into set B ⇔
F ∈ ℘(A× B)
V
(∀p
1
, p
2
∈ F : p
1
6= p
2
⇒ Π
1
(p
1
) 6=
Π
1
(p
2
))
V
{Π
1
(p)|p ∈ F} = A.
Definition 2.5 (Set Function). A set function is a
function in which every range element is a set. For-
mally, let F is a set function ⇔ F is a function and
(∀c ∈ dom(F) : F(c) is a set).
For instance we can express information about com-
panies and their locations by means of a set function
over the domain {Company, Location}, namely.
(Company;{’Natural Join’, ’Central Boekhuis’, ’Or-
acle’, ’Remmen & De Brock’}) (Location, {’New
York’, ’Venice’, ’Paris’})
Definition 2.6 (Table). Given two sets H and K, a
table over H and K is a set of functions T over the
same set H and into the same set K. i.e. ∀ t ∈ T: t is a
function from H to K.
For instance consider a table containing data on em-
ployees:
Table 1: Employee.
emp no emp name emp rank
100 John Manager
101 David programmer
103 Albert HR
The table is represented by the set of functions t
1
,t
2
,t
3
where dom(t
i
) = emp no, emp name, emp rank and
for instance t
1
(emp name) = John.
There is a correspondence between tuples and
functions. For instance, t
1
corresponds to the fol-
lowing tuple: (emp no, 100), (emp name, John),
(emp rank, manager). The first coordinates of the or-
dered pairs in a tuple are referred to as the attributes
of that tuple.
Definition 2.7 (Watermarking). A watermark W
for a table T over H into K, is a predicate such that
W(T) is true and the probability of W(T
′
) being true
with T
′
∈℘(H × K)\T is negligible.
DATABASE AUTHENTICATION BY DISTORTION FREE WATERMARKING
221

3 DISTORTIONS BY
WATERMARKING
It is often hard to define the available bandwidth for
inserting the watermark directly. Instead, allowable
distortion bounds (Sion et al., 2004)(Sion, 2004)for
the input data can be defined in terms of consumer
metrics. If the watermarked data satisfies the met-
rics, then the alterations induced by the insertion of
the watermark are considered to be acceptable. One
such simple yet relevant example for numeric data, is
the case of maximum allowable mean squared error
(MSE), in which the usability metrics are defined in
terms of mean squared error tolerances as
(S
i
−V
i
)
2
< t
i
,∀i = 1...n and (1)
n
∑
i
(S
i
−V
i
)
2
< t
max
(2)
where
S = s
1
,...,s
n
⊂ R , is the data to be watermarked,
V = v
1
,...,v
n
is the result,
T = t
1
,...,t
n
⊂ R and
t
max
∈ R define the guaranteed error bounds at data
distribution time.
In other words T defines the allowable distortions
for individual elements in terms of MSE and t
max
its
overall permissible value.
However, specifying only allowable change lim-
its on individual values, and possibly an overall limit,
fails to capture important semantic features associated
with the data, especially if the data is structured. Con-
sider for example, the age data in an Indian context.
While a small change to the age values may be ac-
ceptable, it may be critical that individuals that are
younger than 21 remain so even after watermarking if
the data will be used to determine behavior patterns
for under-age drinking. Similarly, if the same data
were to be used for identifyinglegal voters, the cut-off
would be 18 years. In another scenario, if a relation
contains the start and end times of a web interaction, it
is important that each tuple satisfies the condition that
the end time be later than the start time. For some
other application it may be important that the relative
ages, in terms of which one is younger, not change.
Other examples of constraints include: uniqueness,
each value must be unique; scale, the ratio between
any two number before and after the change must re-
main the same; and classification, the objects must re-
main in the same class (defined by a range of values)
before and after the watermarking. As is clear from
the above examples, simple bounds on the change of
numerical values are often not sufficient to prevent
side effects of a watermarking operation.
4 DATA PARTITIONING
In this section we present a data partitioning algo-
rithm that partitions the data set based on a secret key
ℜ. The data set D is a database relation with scheme
D(P,C
0
,...,C
v−1
), where P is the primary key attribute,
C
0
,...,C
v−1
are it’s v attributes, and η is the number of
tuples in D. The data set D is to be partitioned into m
non overlapping partitions, [S
0
],...,[S
m−1
], such that
each partition [S
i
] contains on average (
η
m
) tuples from
the data set D. Partitions do not overlap, i.e., for any
two partitions [S
i
] and [S
j
] such that i 6= j we have
[S
i
] ∩ [S
j
] =
/
0. In order to generate the partitions,
for each tuple r ∈ D, the data partitioning algorithm
computes a message authenticated code (MAC) using
HMAC (HMAC, 2002).
Using the property that secure hash functions gen-
erate uniformly distributed message digests this par-
titioning technique places (
η
m
) tuples, on average, in
each partition. Furthermore, an attacker cannot pre-
dict the tuples-to-partition assignment without the
knowledge of the secret key ℜ and the number of
partitions m which are kept secret. Keeping it secret
makes it harder for the attacker to regenerate the parti-
tions. The partitioning algorithm is described below:
Algorithm 1: get partitions(D,ℜ,m).
1: for each tuple r ∈ D do
2: partition ← HMAC(ℜ | r.P) mod m
3: insert r into S
partition
4: end for
5: return (S
0
,...,S
m−1
)
Consider the lattice A = hN,
S
{⊥,⊤}, ⊑i, where ⊥ ⊑
i ⊑ ⊤ and ∀ i, j ∈ N, i 6= j, i and j are uncomparable
with ⊑. The lattice is shown in figure 3.
Figure 3: Lattice of the abstract domain.
Given a data set D∈ (P×C
0
×C
1
×...×C
v−1
) and
m partitions {[S
i
],0 ≤ i ≤ (m− 1)}, for each set T ⊆
D, and given a set of natural number i ∈ N, we can
define a concretization map γ as follows:
γ(⊤) = D
γ(⊥) =
/
0
ICSOFT 2010 - 5th International Conference on Software and Data Technologies
222

γ(i) =

T ⊆ D if ∀t ∈ T : i = HMAC(ℜ|t.P) mod m
/
0 Otherwise
(3)
The best representation of a set of tuples is captured
by the corresponding abstraction function α :
α(T) =



⊥ if S =
/
0
i if ∀t ∈ T : HMAC(ℜ|t.P) mod m = i
⊤ Otherwise
(4)
The two functions α and γ described above yield
a Galois connection (Cousot and Cousot, 1977)
(Cousot and Cousot, 1992) between D, i.e. the actual
data set and the lattice depicted in figure 2.
5 WATERMARK GENERATION
We are interested in a watermark generation process
starting from a partition [S
k
] 0 ≤ k ≤ m], in a rela-
tional database table . The partitioning can be seen as
a virtual grouping which does not change the physi-
cal position of the tuples. Let the owner of the rela-
tion D possess a watermark key ℜ, which will be used
in both watermark generation and detection. In addi-
tion, the key should be long enough to thwart brute
force guessing attacks to the key. A cryptographic
pseudo random sequence generator (Schneier., 1996)
G is seeded with the concatenation of watermark key
ℜ and the primary key r.P for each tuple r ∈ S
k
, gen-
erating a sequence of numbers, through which we se-
lect a field (attribute) in D. A fixed number of MSBs
(most significant bits) and LSBs (least significant bits)
of the selected field are used for generating the water-
mark of that corresponding field. The reason behind
it is, a small alteration in that field in D will affects
the LSBs first and a major alteration will affects the
MSBs, so the LSB and MSB association is able to
track the changes in the actual attribute values. So
here we make the watermark value as the concatena-
tion of m MSBs and n LSBs such that m+ n = 8. Our
aim is to make a gray scale image as the watermark of
that associated partition, so the value of each cell must
belongs to [0 to 255] range.Formally, the watermark
W
k
corresponding to the k
th
partition [S
k
] is generated
as follows,
Algorithm 2: genW(S
k
,ℜ).
1: for each tuple r ∈ S
k
do
2: construct a row t in W
k
3: for (i=0; i< v; i=i+1) do
4: j= G
i
(ℜ,r.P) mod v
5: t.W
i
k
= (mMSBs| nLSBs)
10
mod 256 of the
j
th
attribute in r
6: delete the j
th
attribute from r
7: end for
8: end for
9: return(W
k
)
Let us illustrate the above algorithm for a single tuple
in any hypothetical partition of a table Employee
= (emp id,emp name,salary,location, position),
where emp id is the primary key which is concate-
nated along with the private key ℜ as in line 4 in the
above algorithm to select random attributes. Here
(10111111, 10110101, 10010101,11110111) is the
generated watermark for the tuple (Bob, 10000, Lon-
don, Manager), where we consider 4 MSBs concate-
nated with 4 LSBs. And the attribute watermark pair
looks like {hBob,10010101i, h10000,10111111i,
hLondon,11110111i,hManager,10110101i}. The
entire concept is illustrated by the following diagram
(Figure 4)
Figure 4: Watermark generation for a single tuple.
So if there are n number of tuples in the partition
[S
k
], genW generates a gray scale imageW
n,v
k
as a wa-
termark for [S
k
] partition. The whole process does not
introduce any distortion to the original data. The use
of MSB LSB combination is for thwarting potential
attacks that modify the data as it simply produces an
integrity certificate.
5.1 Functional Abstraction
Theorem 1 (Galois Connection). Given a table D ⊆
C
0
× C
1
× C
2
× ... C
v−1
, let B
v
is the set of all binary
sequences of length v. We can define abstraction and
concretization function between ℘(C
0
× C
1
× C
2
×
... C
v−1
) and℘(B
v
) as follows
α(S) = {genW(S, ℜ)(r) | r ∈ S }
γ(W) = {t ∈ S ⊆ D | genW(S, ℜ)(t) ∈ W}. Then α
and γ form a Galois connection (Cousot and Cousot,
1977) (Cousot and Cousot, 1992).
DATABASE AUTHENTICATION BY DISTORTION FREE WATERMARKING
223

Proof. α(S) ⊆ W
⇔ {genW(S, ℜ)(r) | r ∈ S } ⊆ W
⇔ ∀ r ∈ S : genW(S, ℜ)(r) ∈ W
⇔ S ⊆ { r | genW(S, ℜ)(r) ∈ W}
⇔ S ⊆ γ(W).
The data set (table) D ⊆ ℘(C
0
× C
1
× ...C
v−1
)
and the watermark W ⊆ ℘(B
v
). By Theorem 1
(D,W,α,γ) form a Galois Connection. The function
genW : D → W is the watermark generation function
described above. ∀t ∈ D, f
alt
: D → D and ∀t
#
∈ W,
f
#
alt
:W → W are the alteration functions that alter the
tuples in both concrete and abstract domain, respec-
tively. Therefore the soundness condition with respect
to the alteration function can be stated as follows:
∀t ∈ D : α(f
alt
(t)) ⊑ f
#
alt
(α(t))
Figure 5: Soundness.
This means that, the proposed watermark process
is sound whenever the diagram above commutes.
6 WATERMARK DETECTION
A very important problem in a watermarking scheme
is synchronization, that is, we must ensure, that the
watermark extracted is in the same order as that gen-
erated. If synchronization is lost, even if no modi-
fications have been made, the embedded watermark
cannot be correctly verified. In watermark detection,
the watermark key ℜ and watermark W
k
are needed
to check a suspicious partition S
′
k
of the suspicious
database relation D
′
. It is assumed that the primary
key attribute has not been changed or else can be re-
covered.
Algorithm 3: detW(S
′
k
,ℜ,W
k
).
1: matchC=0
2: for each tuple r ∈ S
k
do
3: get the r
th
row, t of W
k
4: for (i=0; i < v; i = i+1) do
5: j= G
i
(ℜ,r.P) mod v
6: if t.W
i
k
= (mMSBs| nLSBs)
10
mod 256 of the
j
th
attribute in r then
7: matchC = matchC + 1
8: end if
9: delete the j
th
attribute from r
10: end for
11: end for
12: if matchC=ω then
13: // ω = number of rows × number of columns in
W
k
14: return true
15: else
16: return false
17: end if
The variable matchC counts the total number of
correct matches. We consider the watermarkW
t,i
k
, t= 1
to q
k
(number of tuples in S
k
) and i= 1 to v (number of
attributes in relation). At the statement number 6 the
authentication is checked by comparing the generated
watermark bitwise. And after each match matchC is
increased by 1. Finally at statement number 12, the
total match is compared to the number of bits in the
watermark image W
k
associated with partition S
k
to
check the final authentication.
7 ZERO DISTORTION
AUTHENTICATION
WATERMARKING (ZAW)
So far, we have a set of gray scale images correspond-
ing to a data table D. Each gray scale image W
k
(k=1
to m) is associated with m partitions S
k
(k=1 to m) of
D. And image W
k
is said to be the abstraction of parti-
tion S
k
. Now the authentication of database owner is
necessary. We employ the zero-distortion authentica-
tion watermarking (ZAW) (Wu, 2003) to authenticate
the table which introduces no artifact at all. Figure 6
describes the framework of the ZAW scheme which
does not modify the host content but transforms the
host into its equivalence.
Figure 6: ZAW framework.
Without loss of generality we assume that the ta-
ble D is fragmented into m independent gray scale
ICSOFT 2010 - 5th International Conference on Software and Data Technologies
224

images W
0
; W
1
; ...;W
m−1
.Each image does not depend
on any other images. If we consider D as the concrete
table then W (composition of all image fragmentsW
0
;
W
1
; ...;W
m−1
) can be considered as its abstract coun-
terpart (Theorem 1). An equivalent image W’ can be
derived from π
k
using Myrvold and Ruskey’s linear
permutation ranking algorithm (Myrvold and Ruskey,
2000). The algorithm unrank makes a permutation
of the segments based on a secret number (M) only
known to the database owner and this number can be
considered as a private key of the owner. The owner
can distribute the number of partitions m (section 4)
as public key. unrank can be treated as a encryption
algorithm based on the private key M.
Algorithm 4: Unrank(m,M,π).
1: for (i=0; i<m ; i++) do
2: π
i
= i
3: end for
4: if m > 0 then
5: swap(π[m− 1], π[M mod m])
6: Unrank(m− 1, ⌊M/m⌋, π)
7: end if
End
The algorithm rank can be treated as decryption
algorithm based on the public key m.
Algorithm 5: rank(m,π,π
−1
).
1: if m = 1 then
2: return 0
3: end if
4: s = π[m− 1]
5: swap(π[m− 1], π[π
−1
[m− 1]])
6: swap(π
−1
[s],π
−1
[m− 1])
7: return(s+m * rank(m− 1, π, π
−1
))
8 ROBUSTNESS
We analyze the robustness of our scheme by Bernoulli
trials and binomial probability. Repeated indepen-
dent trials in which there can be only two outcomes
are called Bernoulli trials in honor of James Bernoulli
(1654-1705).The probability that the outcome of an
experiment that consists of n Bernoulli trials has k
successes and n - k failures is given by the binomial
distribution
b(n,k, p) =

n
k

p
k
(1− p)
n−k

n
k

=
n!
k!(n− k)!
0 ≤ k ≤ n
where the probability of success on an individual trial
is given by p.
The probability of having at least k successes in
n trials, the cumulative binomial probability, can be
written as
B(n,k, p) =
k
∑
i
b(n,i, p)
We will discuss our robustness condition based on
two parameters false hit and false miss.
8.1 False Hit
False hit is the probability of a valid watermark being
detected from non-watermarked data. The lower the
false hit, the better the robustness. When the water-
mark detection is applied to non-watermarked data,
each hMSB
m
|LSB
n
i (m+n=8) association in data has
the probability
1
2
8
to match to the corresponding bit
in the watermark. Assume that the non-watermarked
data partition S
q
has the same number q of tuples and
has the same primary keys as the original data. Let
ω = v(m + n)q is the size of the watermark. where
v is the number of attributes being watermarked and
q is the number of tuples in partition S
q
. The false
hit is the probability that at least
1
T
portion of ω can
be detected from the non-watermarked data by sheer
chance. When T is the watermark detection parame-
ter. It is used as a tradeoff between false hit and false
miss. Increasing T will make the robustness better in
terms of false hit. Therefore, the false hit F
h
can be
written as
F
h
= B(ω,⌊
ω
T
⌋,
1
2
8
)
8.2 False Miss
False miss is the probability of not detecting a valid
watermark from watermarked data that has been mod-
ified in typical attacks. The less the false miss, the
better the robustness.
8.2.1 Subset Deletion Attack
For tuple deletion and attribute deletion, the
hMSB
m
|LSB
n
i(m+n=8) association in the deleted tu-
ples or attributes will not be detected in watermark
detection; however, the other tuples or attributes will
not be affected. Therefore, all detected bit strings will
match their counterparts in the watermark, and the
false miss is zero.
DATABASE AUTHENTICATION BY DISTORTION FREE WATERMARKING
225

8.2.2 Subset Addition Attack
Suppose an attacker inserts ς new tuples to replace ς
watermarked tuples with their primary key values un-
changed. For watermark detection to return a false an-
swer, at least
1
T
bit strings of those newly added tuples
(which consists of vς hMSB
m
|LSB
n
i) must not match
their counterparts in the watermark (which consists of
ω = v(m+ n)q bits, if the partition contains q tuples).
also in this case T is the watermark detection parame-
ter, used as a tradeoff between false hit and false miss.
Increasing T will make the robustness worse in terms
of false miss. Therefore, the false miss F
m
for insert-
ing ς tuples can be written as
F
m
= B(vς,⌊
vς
T
⌋,
1
2
8
)
The formulae F
h
and F
m
together, give us a mea-
sure of the robustness of the watermark.
9 CONCLUSIONS
As a conclusion, let us stress the main features of the
watermark technique presented in this paper,
• it does not depend on any particular type of at-
tributes (categorical, numerical);
• it ensures both authentication and integrity;
• it is partition based, we are able to detect and
locate modifications as we can trace the group
which is possibly affected when a tuple t
m
is tam-
pered;
• neither watermark generation nor detection de-
pends on any correlation or costly sorting among
data items. Each tuple in a table is independently
processed; therefore, the scheme is particularly
efficient for tuple oriented database operations;
• it does not modify any database item; therefore it
is distortion free.
ACKNOWLEDGEMENTS
Work partially supported by Italian MIUR COFIN ’07
project ”SOFT” and by RAS project TESLA.
REFERENCES
Agrawal, R., Haas, P. J., and Kiernan, J. (2003). Water-
marking relational data: framework, algorithms and
analysis. The VLDB Journal, 12(2):157–169.
Bhattacharya, S. and Cortesi, A. (2009a). A distortion free
watermark framework for relational databases. In IC-
SOFT (2), pages 229–234.
Bhattacharya, S. and Cortesi, A. (2009b). A generic
distortion free watermarking technique for relational
databases. In ICISS, pages 252–264.
Collberg, C. S. and Thomborson, C. (2002). Watermarking,
tamper-proofing, and obfuscation - tools for software
protection. Software Engineering, IEEE Transactions
on, 28:735–746.
Cousot, P. (2001). Abstract interpretation based formal
methods and future challenges. In Informatics -
10 Years Back. 10 Years Ahead., pages 138–156.
Springer-Verlag.
Cousot, P. and Cousot, R. (1977). Abstract interpretation: a
unified lattice model for static analysis of programs by
construction or approximation of fixpoints. In POPL
’77: Proceedings of the 4th ACM SIGACT-SIGPLAN
symposium on Principles of programming languages,
pages 238–252. ACM.
Cousot, P. and Cousot, R. (1992). Abstract interpreta-
tion frameworks. Journal of Logic and Computation,
2:511–547.
Cousot, P. and Cousot, R. (2004). An abstract
interpretation-based framework for software water-
marking. In POPL ’04: Proceedings of the 31st ACM
SIGPLAN-SIGACT symposium on Principles of pro-
gramming languages, pages 173–185. ACM.
Cousot, P. and Cousot, R. (2007). Abstract interpretation
and application to static analysis. In 1st IEEE and
IFIP International Symposium on Theoretical Aspects
of Software Engineering.
Cox, I. J., Miller, M. L., and Bloom, J. A. (2001). Digi-
tal Watermarking: Principles and Practice. Morgan
Kaufmann Publishers.
Gross-Amblard, D. (2003). Query-preserving watermark-
ing of relational databases and xml documents. In
PODS ’03: Proceedings of the twenty-second ACM
SIGMOD-SIGACT-SIGART symposium on Principles
of database systems, pages 191–201. ACM.
Haan, L. D. and Koppelaars, T. (2007). Applied Mathemat-
ics for database Professionals. Apress.
HMAC (2002). The keyed-hash message authentication
code. Federal Information Process Standards Publi-
cation.
Johnson, Duric, and Jajodia (2000). Information Hiding:
Steganography and WatermarkingAttacks and Coun-
termeasures. Kluwer Publishers.
Myrvold, W. and Ruskey, F. (2000). Ranking and unranking
permutations in linear time. Information Processing
Letters, 79:281–284.
Schneier., B. (1996). Applied Cryptography. John Wiley
and Sons.
Sion, R. (2004). Proving ownership over categorical data. In
In Proceedings of the IEEE International Conference
on Data Engineering ICDE, pages 584–596.
Sion, R., Atallah, M., and Prabhakar, S. (2004). Rights pro-
tection for relational data. In In Proceedings of ACM
SIGMOD, pages 98–109. ACM Press.
Wu, Y. (2003). Zero-distortion authentication watermark-
ing. In Proc. International Conference on Information
Security, LNCS 2851, pages 325–337.
ICSOFT 2010 - 5th International Conference on Software and Data Technologies
226