
FAST EDGE-GUIDED INTERPOLATION OF COLOR IMAGES
Amin Behnad and Konstantinos N. Plataniotis
The Edward S. Rogers Sr. Department of Electrical and Computer Engineering, University of Toronto
10 King’s College Road, Toronto, Ontario, M5S 3G4, Canada
Keywords:
Color images, Interpolation, Real-time applications.
Abstract:
We propose a fast adaptive image interpolation method for still color images which is suitable for real-time
applications. The proposed interpolation scheme combines the speed of fast linear image interpolators with
advantages of an edge-guided interpolator. A fast and high performance image interpolation technique is
proposed to interpolate the luminance channel of low-resolution color images. Since the human visual system
is less sensitive to the chrominance channels than the luminance channel, we interpolate the former with the
fast method of bicubic interpolation. This hybrid technique achieves high PSNR and superior visual quality
by preserving edge structures well while maintaining a low computational complexity. As verified by the
simulation results, interpolation artifacts (e.g. blurring, ringing and jaggies) plaguing linear interpolators are
noticeably reduced with our method.
1 INTRODUCTION
Image interpolation has been an active research topic
since early days of image processing, due to a wide
range of its applications, including resolution upcon-
version, resizing, video deinterlacing, video frame
rate upconversion, subpixel motion estimation, im-
age compression, etc. Many of these applications
have real-time requirements, for examples, video de-
interlacing and resolution or/and frame rate upcon-
version. The common solutions for real-time image
interpolation are simple image-independent linear fil-
ters, such as bilinear interpolator and bicubic inter-
polator (Keys, 1981). But these simple linear filters
are isotropic and ill suited for directional image wave-
forms and also cannot cope with the nonlinearities of
the image formation model (Plataniotis et al., 1999).
Hence they tend to produce severe interpolation arti-
facts in areas of edges and fine image details.
To overcome the above said weaknesses of signal-
independent isotropic interpolators, adaptive nonlin-
ear interpolators were introduced (Li and Orchard,
2001), (Muresan, 2005), (Zhang and Wu, 2006) and
(Li and Nguyen, 2008) . Among these algorithms,
edge preserving interpolators are of great interest.
The ultimate goal of an edge-guided image inter-
polation technique is to avoid interpolation against
the existing edge directions for each missing high-
resolution (HR) pixel. This achieves clean and sharp
reproduced edges in the HR output image. How-
ever in practice there is a major issue with most of
the developed edge-guided interpolators. The edge-
guided interpolators achieve better perceptual quality
than linear filters at cost of higher computationalcom-
plexity. Therefore most of these algorithms are not
suitable for real-time applications.
In this work, we address this issue and devise
an algorithm to reduce the computational cost of di-
rectional image interpolation for color images. In
the proposed algorithm, low-resolution (LR) color
images are converted to the luminance-chrominance
space, from the RGB counterpart and the interpola-
tion process is carried out in the new space. The rea-
son for this mapping is twofold. First, the human vi-
sual system is much more sensitive to the luminance
component than the chrominance. Hence, we apply
a sophisticated interpolation technique to interpolate
the luminance channel and for computational savings,
a simple linear filter e.g. bicubic is applied for the
chrominance channels. Second, the luminance chan-
nel captures the variations in the image and magni-
fies the edges and other high-frequency components.
This achieves more reliability on the extracted edge
information from the LR image, which is crucial for
directional image interpolation.
To interpolate the luminance channel, we also pro-
pose a fusion-based image interpolation method. As
verified by the simulations, this technique achieves
superior performance than the competing methods, at
lower computational complexity.
103
Behnad A. and N. Plataniotis K. (2010).
FAST EDGE-GUIDED INTERPOLATION OF COLOR IMAGES.
In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 103-107
DOI: 10.5220/0002933401030107
Copyright
c
SciTePress

The presentation of this paper is as follows. The
proposed interpolation scheme for color images is de-
scribed in section. 2. Proposed edge-guided interpo-
lation algorithm for gray-scaled images is presented
in section.3. Section.4 presents the simulation results
and section.5 concludes.
2 PROPOSED ALGORITHM FOR
COLOR IMAGE
INTERPOLATION
As in the existing literature, we assume that each
pixel in the input color image has three color val-
ues: red (R), green (G) and blue (B). In pursuit of
low computational cost, we interpolate color images
in a new space which must include smooth (low-pass)
components. As such, we can effectively interpolate
the smooth components with fast linear interpolators,
without sacrificing the perceptual quality. The conve-
nient RGB to YCbCr conversion faithfully satisfy the
above condition. The equations for this mapping in
the JPEG JFIF format (Hamilton, 1992) are:
Y = 0.299R + 0.587G+ 0.114B
Cb = − 0.1687R− 0.3313G+ 0.5B
Cr = 0.5R− 0.4187G− 0.0813B (1)
and the reverse equations are given as:
R = Y + 1.402Cr
G = Y − 0.34414Cb− 0.71414Cr
B = Y + 1.772Cb (2)
However, the applied coefficients in (1) and (2) are
real numbers which incurs error for hardware imple-
mentations. This issue can be addressed by applying
a reversible transformation such as RGB to YCoCg
with corresponding conversion formula:
Y = 0.25R+ 0.5G+ 0.25B
Co = 0.5R− 0.5B
Cg = − 0.25R+ 0.5G− 0.25B (3)
and reverse formula
R = Y +Co− Cg
G = Y +Cg
B = Y −Co− Cg. (4)
For more details about developing of (3) and (4)
please refer to (Malvar et al., 2008). The advan-
tage of YCoCg transform over YCbCr is that the in-
verse formula, mapping YCoCg into RGB only re-
quires additions and subtractions. To be more pre-
cise, the inversion can be performed with four ad-
ditions: G = Y + Cg, t = Y − Cg, R = t + Co and
B = t − Co (Malvar et al., 2008). We use this re-
versible transformation for the proposed interpolation
technique. Color images are converted from RGB
to YCoCg space, then the chrominance channels (Co
and Cg) are interpolated with bicubic interpolator.
By now, we have described the interpolation pro-
cess of the chrominance channels. Human visual sys-
tem is more sensitive to the luminance (Y) channel.
Hence in our design a high-performance edge-guided
interpolation algorithm is utilized for interpolation of
the luminance channel. In the next section the pro-
posed image interpolation algorithm for the Y chan-
nel is presented.
3 FAST ADAPTIVE
INTERPOLATION OF
GRAY-SCALED IMAGES
In this section we reexamine the problem of resolution
upconversion of gray-scaled images. Formation of an
HR image from original LR samples is depicted in
figures. 1(a). The missing pixels are recovered in two
batches. First missing pixels with coordinates (2i, 2j)
are recovered and in the second batch, pixels with co-
ordinates (2i−1, 2j) and (2i, 2j− 1) are interpolated.
As illustrated in figures. 1(b) and (c), the problem of
interpolation of the second batch becomes the same
as the first bacth by 45
◦
rotation. Therefore, we only
describe the algorithm for the first batch in detail.
Figure 1: (a) Formation of a high-resolution (HR) image
from low-resolution (LR) samples (empty circles) and miss-
ing HR pixels (black circles). (b),(c) Interpolation of HR
missing pixels with different coordinates. Two estimates
are made from the LR samples (hatches circles) for each
missing pixel.
Two estimates for each missing pixel are obtained
by cubic convolution (Keys, 1981) in two orthogo-
nal directions (figures. 1(b) and (c)): d
1
and d
2
.
In (Zhang and Wu, 2006) a linear minimum mean-
squares method of fusing these two directional esti-
mates is proposed. For low complexity and ease of
implementation, we also adopt affine weights to lin-
early fuse d
1
and d
2
to interpolate the HR pixel Y
HR
,
namely:
SIGMAP 2010 - International Conference on Signal Processing and Multimedia Applications
104

0 5 10 15
30.75
30.8
30.85
30.9
30.95
31
31.05
31.1
31.15
31.2
|γ|
PSNR
Figure 2: Average PSNR result over a set of training images
for different values of γ.
Y
HR
= αd
1
+ (1− α)d
2
, α ∈ [0, 1]. (5)
The value of α is computed as follows. First, the
smoothness along directions 1 and 2 are measured by
computing the sum of the absolute differences (SAD)
of the available LR pixels in the locality of the miss-
ing HR pixel Y
HR
(2i, 2j) as:
SAD
1
(2i, 2j) =
∑
(m,n)∈W
2i,2 j
Y
LR
(m, n) −Y
LR
(m+ 1, n+1)
(6)
and
SAD
2
(2i, 2j) =
∑
(m,n)∈W
2i,2 j
Y
LR
(m, n) −Y
LR
(m− 1, n+1)
(7)
where W
2i,2j
is a 7× 7 spatial template in the HR lat-
tice centered at the position (2i, 2j). As described in
the section.1, edge-guided interpolators perform the
interpolation filtering along the directions of smooth-
ness. Hence, it is expected that more wight be as-
signed to the direction with less corresponding value
of SAD
k
, which means:
ˆ
α ∝ SAD
γ
1
, γ < 0 in our de-
sign. Once γ is given,
ˆ
α is computed as:
ˆ
α =
SAD
γ
1
SAD
γ
1
+ SAD
γ
2
. (8)
The following subsection concerns with evaluating
the global optimum value of γ for the proposed al-
gorithm.
3.1 Calculation of γ
In our design, the value of γ is determined by train-
ing. A large set of HR images is selected and down-
sampled by the factor of two and then reconstructed
by the proposed method. The training is accom-
plished on the activity regions of the aforementioned
HR images. The average PSNR over the all training
images for different values of γ is plotted in figures 2.
We choose γ = −4 that achieves the highest objective
performance for the proposed method.
Figure 3: Six sample images in the test set: (a) Lena, (b)
Parrots, (c) Flight, (d) Window, (e) Flower and (f) Fruits.
4 SIMULATION RESULTS
The proposed interpolation method was implemented
and tested on a variety of scenes. A brief objec-
tive comparison between the proposed method in
section.3 and some existing interpolation algorithms
is presented by Table 1. Please note that the reported
PSNR results are for the luminance channel of the
pictures depicted in figures. 3. As verified by the re-
sults, the proposed method outperforms the competi-
tion with NEDI (Li and Orchard, 2001) and method
of (Zhang and Wu, 2006) which are among the best
edge-guided image interpolation algorithms in the lit-
erature. The reported execution time also verifies the
simplicity of the proposed algorithm. The major pa-
rameters of the exploited server for the simulations
are: CPU: Intel
R
Core 2 Duo E8400 (3 GHz), RAM:
4 GB, 6 MB of L2 cache and 1333 MHz front side bus
(FSB). The proposed algorithm is highly paralleliz-
able, since it recovers each missing pixel in isolation.
Therefore the proposed algorithm is also suitable for
hardware implementations.
Table 1: PSNR (decibels) results of reconstructed images
and the average execution time for NEDI (Li and Orchard,
2001), LMMSE INTR (Zhang and Wu, 2006) and the pro-
posed method.
Image NEDI LMMSE INTR Proposed
Lena 33.36 33.38 33.93
Parrot 34.52 34.15 35.21
Flight 29.95 29.92 30.36
Window 34.68 34.92 35.88
Flower 27.96 28.12 28.77
Fruits 36.35 36.81 38.92
Average 32.80 32.88 34.01
Time(s) 21.03 10.52 0.92
FAST EDGE-GUIDED INTERPOLATION OF COLOR IMAGES
105
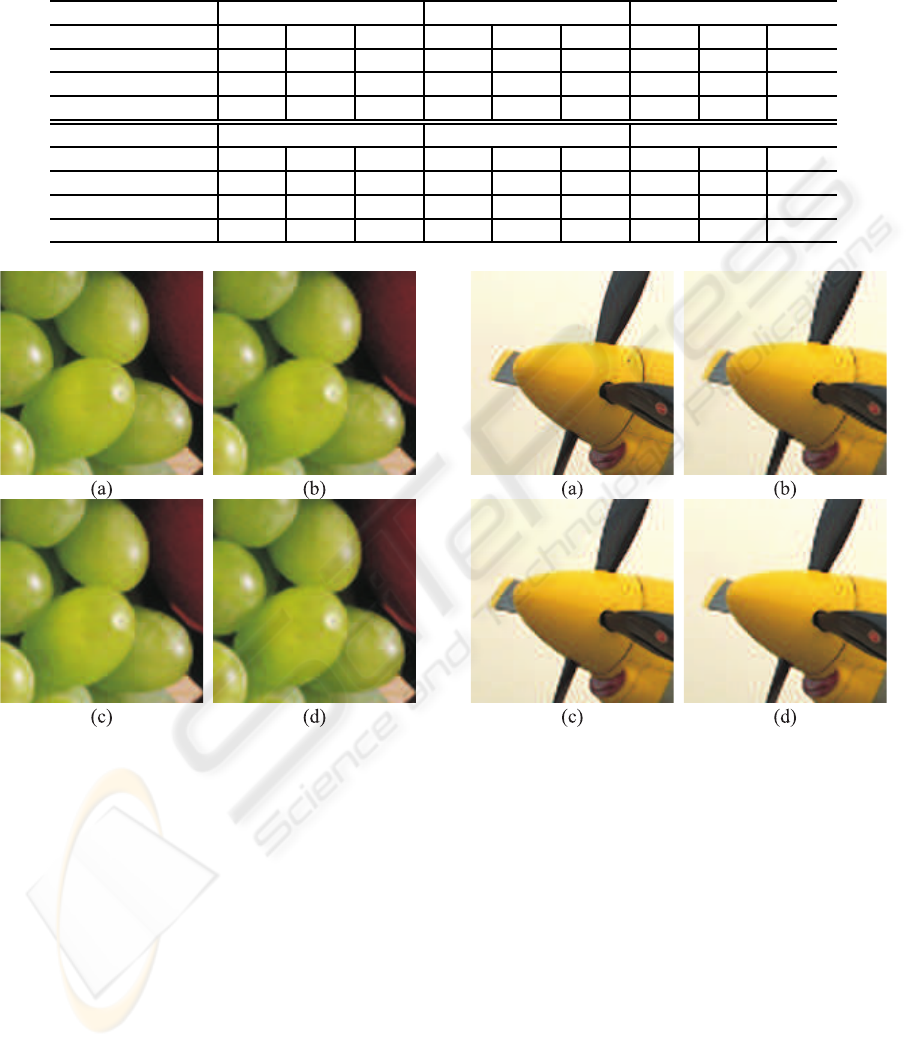
Table 2: PSNR (decibels) results of reconstructed color images in figures. 3 in YCoCg color space with three different
methods. bicubic: all channels are interpolated with bicubic. bicubic+proposed: Y channel is interpolated by the proposed
method in section. 3 and chrominance channels are interpolated with bicubic. proposed: all channels are recovered with the
proposed algorithm in section. 3.
Image Lena Parrot Flight
channels R G B R G B R G B
bicubic 35.47 32.19 30.72 34.13 34.09 34.04 29.69 29.54 29.33
bicubic+proposed 35.53 32.70 31.07 34.99 34.96 34.89 30.55 30.43 30.20
proposed 35.89 32.70 31.18 34.98 34.92 34.85 30.54 30.43 30.19
Image Window Flower Fruits
channels R G B R G B R G B
bicubic 34.94 34.92 34.75 28.10 27.10 30.15 36.79 37.20 38.51
bicubic+proposed 35.61 35.63 35.44 28.15 27.25 29.92 37.45 37.88 38.70
proposed 35.62 35.62 35.37 28.13 27.19 30.25 37.48 37.91 38.87
Figure 4: Interpolation results of a portion of the image
Fruits with three different methods: (a) bicubic, (b) bicu-
bic+proposed, (c) proposed. (a) is the original image.
To evaluate the performance of the proposed inter-
polation scheme for color images we conduct the fol-
lowing test. The color images listed in the figures.3
are first down-sampled by a factor of two, and recov-
ered by three different schemes:
1. Bicubic: the R,G and B channels are interpolated
with bicubic interpolator.
2. Bicubic+Proposed: images are first converted to
the YCoCg space and the Y channel is upcon-
verted by the proposed edge-guided interpolator
while the Co and Cg channels are interpolated by
bicubic.
3. Proposed: images are first converted to the
YCoCg space and the Y,Co and Cg channels are
Figure 5: Interpolation results of a portion of the image
Flight with three different methods: (a) bicubic, (b) bicu-
bic+proposed, (c) proposed. (a) is the original image.
interpolated with the proposed edge-guided inter-
polator.
The results are tabulated in Table.2. It can be verified
that the combinatory algorithm (bicubic+proposed)
achievessimilar results to those of the third algorithm.
The perceptual quality of the recovered image by the
three algorithms are compared in figures. 4,5 and 6.
The outputs of the schemes 2 and 3 are visually sim-
ilar which manifests the efficacy of the proposed al-
gorithm for reducing the complexity of color image
interpolation without loss of visual quality. The re-
constructed images by the proposed simplified image
interpolation method are in turn greatly sharper and
cleaner than those of bicubic interpolation.
SIGMAP 2010 - International Conference on Signal Processing and Multimedia Applications
106

Figure 6: Interpolation results of a portion of the image
Bush with three different methods: (a) bicubic, (b) bicu-
bic+proposed, (c) proposed. (a) is the original image.
5 CONCLUDING REMARKS
A fast interpolation algorithm for color images is pro-
posed. Color images are first converted from RGB to
luminance-Chrominance format, then the luminance
channel is interpolated with a proposed edge-guided
interpolation technique and the luminance channels
are interpolated with simple bicubic interpolation.
Since chrominance channels have low-pass 2D wave-
forms, we can effectively interpolate them without de-
grading the perceptual quality of the recovered im-
ages. Simulation results verify that the proposed in-
terpolation technique is fast and also removes com-
mon interpolation artifacts.
REFERENCES
Hamilton (1992). Jpeg file interchange format, version 1.02.
Keys, R. G. (1981). Cubic convolution interpolation for
digital image processing. In IEEE Trans. on Acous-
tic, Speech, Signal Processing, vol. 29, no.6, pp.1153–
1160.
Li, M. and Nguyen, T. Q. (2008). Markov random field
model-based edge-directed image interpolation. In
IEEE Trans. on Image Processing, vol. 17, no. 7, pp.
1121–1128.
Li, X. and Orchard, M. T. (2001). New edge-directed in-
terpolation. In IEEE Trans. on Image Processing, vol.
10, pp. 1521–1527.
Malvar, H. S., Sullivan, G. J., and Srinivasan, S. (2008).
Lifting based reversible color transformations for im-
age compression. In SPIE Applications of Digital Im-
age Processing, vol. 7073, pp. 707307–707307-10.
Muresan, D. D. (2005). Fast edge directed polynomial inter-
polation. In IEEE International Conference on Image
Processing, vol. 2, pp. II-990-3.
Plataniotis, K. N., Androutsos, D., and Venetsanopoulos,
A. N. (1999). Adaptive fuzzy systems for multichan-
nel signal processing. In Proceedings of the IEEE, vol.
87, no. 9, pp. 1601-1622.
Zhang, L. and Wu, X. (2006). An edge-guided image in-
terpolation algorithm via directional filtering and data
fusion. In IEEE Trans. on Image Processing, vol. 15,
no. 8, pp. 2226–2238.
FAST EDGE-GUIDED INTERPOLATION OF COLOR IMAGES
107
