FREQUENCY EXTRACTION BASED ON ADAPTIVE FOURIER

SERIES

Application to Robotic Yoyo

Tadej Petriˇc, Andrej Gams and Leon

Zlajpah

Department of Automation, Biocybernetics and Robotics, Joˇzef Stefan Institute, Jamova cesta 39, 1000 Ljubljana, Slovenia

Keywords:

Fourier series, Nonlinear dynamical systems, Adaptive frequency oscillators, Imitation, Yo-yo.

Abstract:

We present a novel method to obtain the basic frequency of an unknown periodic signal with an arbitrary

waveform. The method originates from nonlinear dynamical systems for frequency extraction, which are

based on adaptive frequency oscillators in a feedback loop. While using several adaptive frequency oscillators

in a loop results in extraction of separate frequency components, our method extracts the basic frequency of

the input signal without any additional logical operations. The proposed method uses a whole Fourier series

representation in the feedback loop. In this way it can extract the frequency and the phase of an unknown

periodic signal, in real-time, and without any additional signal processing or preprocessing. The method also

determines the Fourier series coefﬁcients and can be used for dynamic Fourier series implementation. It can

be used for the control of rhythmic robotic tasks, where only the extraction of the fundamental frequency is

crucial. This is demonstrated on a highly nonlinear and dynamic task of playing the robotic yo-yo.

1 INTRODUCTION

Controlling rhythmic robotic tasks that require syn-

chronization with the actuated device or interac-

tion with the external environment is a difﬁcult

task, and requires complex sensory systems and ad-

vanced knowledge (Petriˇc et al., 2009). For example,

such rhythmic tasks include handshaking (Kasuga

and Hashimoto, 2005), locomotion (Ijspeert, 2008),

drumming(Degallier et al., 2008), or playing with dif-

ferent toys, like the yo-yo(

Zlajpah, 2006) or the gyro-

scopic device called Powerball (Gams et al., 2007).

Controlling these tasks with robots requires both ac-

curate trajectory generation and frequency tuning.

Determining the fundamental frequency of a task

is a complex problem and can be achieved in differ-

ent ways, e.g. with signal processing methods, such

as FFT, or with the use of nonlinear oscillators (Mat-

suoka et al., 2005). Furthermore, trajectory genera-

tion and modulation are still difﬁcult tasks in robotics.

One possible approach to trajectory generation and

the modulation is the imitation (Schaal, 1999), which

can be preformed in several different ways, using

encoding methods like splines (Ude et al., 2000) or

dynamic movement primitives (DMP) (Schaal et al.,

2007).

Not many approaches that combine both frequency

extraction and waveform learning exist. One of them

is the use of a two-layered imitation system based on

nonlinear dynamical systems (Gams et al., 2009). In

their work, the authors explained that the imitation

system can be used for extracting the frequency of

the input signal, learning its waveform, and imitating

the waveform at the extracted or any other frequency.

Similar, but with less properties for trajectory genera-

tion and modulationcan be achievedby using only the

ﬁrst layer of this system for both frequency extraction

and waveform learning (Righetti et al., 2006). The de-

scribed systems are based on adaptive frequency os-

cillators in a feedback loop. Such an approach can

determine several frequency components of an input

signal. Despite favorable properties of these systems,

there is a considerable drawback in determining the

basic or fundamental frequency of the input signal.

For complex periodic signals with several fre-

quency components, the ﬁrst layer of the imitation

system, referred to as the canonical dynamical sys-

tem, has to include a high number of oscillators in the

feedback loop. Using this system for movement imi-

tation requires determining the basic frequency. This

is accomplished by a logical algorithm that follows

the feedback loop. With a high number of oscilla-

Petri

c T., Gams A. and Žlajpah L. (2010).

FREQUENCY EXTRACTION BASED ON ADAPTIVE FOURIER SERIES - Application to Robotic Yoyo.

In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 32-38

DOI: 10.5220/0002933900320038

 SciTePress

tors, and when several of the oscillators tune to the

same frequency, this can become extremely complex.

A high number of oscillators is practically necessary

and cannot be avoided.

The contribution of this paper is the novel design

of the canonical dynamical system for the two-layered

imitation system. The proposed approach does not re-

quire a logic algorithm to determine the fundamental

frequency of the input signal, as in the original ap-

proach (Gams et al., 2009). We use a single adaptive

phase oscillator in a feedback loop. The oscillator is

followed by a complete Fourier series approximation,

with a built-in algorithm to determine the Fourier co-

efﬁcients. The combination of an adaptive phase os-

cillator and the adaptive Fourier series allows us to

extract the fundamental frequency of the input signal

and use it to control rhythmic robotic tasks.

With this approach we essentially implemented a

real-time, adaptive Fourier series analysis. Our sys-

tem is able to calculate the Fourier coefﬁcients of an

unknown periodic signal in real-time and is computa-

tionally inexpensive. The usefulness of this system is

presented on the case of playing the yo-yo. Control-

ling the yo-yo has already been a subject of several

studies (

Zlajpah, 2006; Jin et al., 2009), which mostly

rely on complex, specially designed controllers based

on the models of the device. The task of playing

yo-yo is highly non-linear and requires on-line fre-

quency adaptation. The proposed approach simpliﬁes

the synchronization between the upward jerk of the

robot and the movement of the yo-yo by determining

the frequency of the up-down motion from a measur-

able periodic quantity.

The paper is organised as follows. In section 2,

we give a brief description of the original two-layered

imitation system with an emphasis on the ﬁrst layer -

the canonical dynamical system. In section 3 we de-

scribe the novel approach using the Fourier series in

the feedback loop. In section 4 we evaluate the pro-

posed approach in simulation, and on a real-world ex-

periment of playing the yo-yo. Conclusions and sum-

mary are in section 5.

2 TWO-LAYERED IMITATION

SYSTEM

The two-layered imitation system was presented in

detail in (Gams et al., 2009). In their work the au-

thors explained that the system can be used for ex-

tracting the frequency spectrum of the input signal,

learning the waveform of one period, and imitating

the desired waveform at an arbitrary frequency. The

system structure is presented in Figure 1. The ﬁrst

layer, i.e. the canonical dynamical system, is used

for frequency extraction. It is based on a set of adap-

tive frequency oscillators in a feedback loop. The sec-

ond layer is called the output dynamical system and is

used for learning and repeating the desired waveform.

The latter is based on dynamic movement primitives

- DMPs, e.g. (Schaal et al., 2007).

Canonic

dynamic

system

Output

dynamic

system

Ω

Figure 1: Two-layered structure of the imitation system.

The input y

is a measured quantity and the output is the

desired trajectory x of the robot. The input φ

is the ad-

ditional phase lag and r is the amplitude of the trajectory.

The system can work in parallel for an arbitrary number of

dimensions.

The ﬁrst layer of the system has two major tasks.

It has to extract the fundamental frequency Ω of the

input signal and it has to exhibit stable limit cycle be-

havior in order to provide the phase signal Φ. The

basis of the canonical dynamical system is a set of

adaptive phase oscillator with applied learning rule as

introduced in (Buchli and Ijspeert, 2004). In order

to accurately determine the frequency, it is combined

with a feedback structure (Buchli et al., 2008) (see

Figure 2). The feedback structure of M adaptive fre-

quency oscillators is governed by

= ω

− K · e· sinφ

, (1)

= −K · e· sinφ

, (2)

e = y

− ˆy, (3)

ˆy =

∑

i=1

cosφ

, (4)

= η · e· cosφ

, (5)

where K is the coupling strength, φ

, i = 1...M is the

phase of separate oscillators, y

is the input signal, M

is the number of oscillators, α

is the amplitude as-

sociated with the i-th oscillator, and η is the learning

constant.

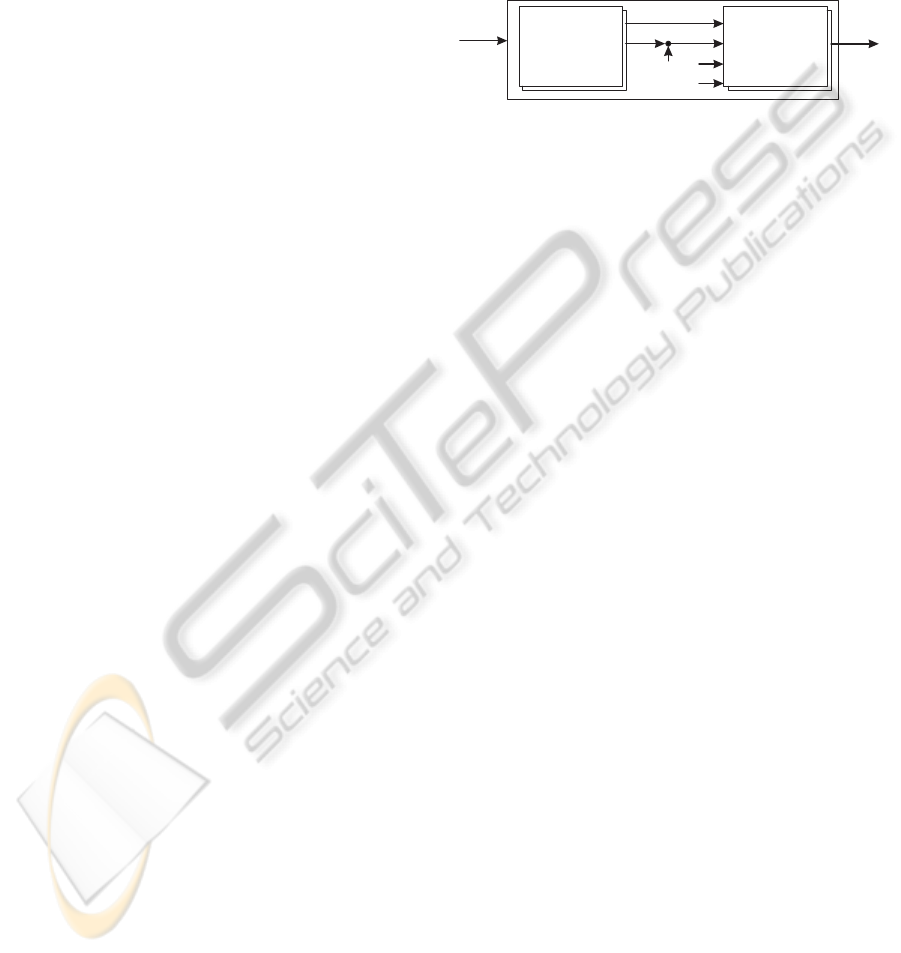
As shown in Figure 2, each of the oscillators in

the feedback structure receives the same input, i.e. the

difference between the input signal and the weighted

sum of separate frequency components. Such a feed-

back structure preforms a kind of Fourier analysis.

The number of extracted frequencies depends on how

many oscillators are used. As only the fundamental

frequency is of interest, the feedback structure is fol-

lowed by a logic algorithm. Determining the correct

frequency and the phase is crucial, because they are

FREQUENCY EXTRACTION BASED ON ADAPTIVE FOURIER SERIES - Application to Robotic Yoyo

ˆy

Ω, Φ

∑

cos(φ

)

, φ

Logic

Figure 2: Feedback structure of M nonlinear adaptive fre-

quency oscillators. Note the logic algorithm that follows the

feedback loop.

Ω

ˆy

,β

Figure 3: Feedback structure of nonlinear adaptive fre-

quency oscillator combined with dynamic Fourier series.

Note that no logic algorithm needed.

the basis for the output dynamic system and the de-

sired behavior of the actuated device.

One possible approach is to choose the ﬁrst non-

zero frequency as was presented in (Gams et al.,

2009). However, it has a drawback that when more

than one oscillators converge to, or oscillate, around

the same frequency, the logic algorithm switches be-

tween the oscillators, and consequently the phase will

not be smooth, leading to oscillations in the output

trajectory.

3 CANONICAL DYNAMICAL

SYSTEM BASED ON FOURIER

SERIES

In this section a novel architecture for canonical dy-

namical system is presented. As the basis of the

canonical dynamical system we use a single nonlin-

ear phase oscillator with applied learning rule (Buchli

and Ijspeert, 2004). This is combined with a feed-

back structure based on an adaptive Fourier series in

order to accurately determine the frequency. A feed-

back structure with an adaptive frequency oscillator

combined with an adaptive Fourier series is shown in

Figure 3. The feedback structure of an adaptive fre-

quency phase oscillator is governed by

φ = Ω − K · e· sinφ, (6)

Ω = −K · e· sinφ, (7)

e = y

− ˆy, (8)

where K is the coupling strength, φ is the phase of the

oscillator, e is the input into the oscillator and y

the input signal. If we compare Eqs. (1, 2) and Eqs.

(6, 7), we can see that the frequency Ω and the phase

φ are now clearly deﬁned. The feedback loop ˆy is now

represented by the Fourier series

ˆy = α

∑

i=1

(α

cos(iφ) + β

sin(iφ)), (9)

and not by the sum of separate frequency components

as in Eq. 4. M is the size of the Fourier series and α

is the amplitude associated with the ﬁrst segment of

the series, it is governed by

= η · e, (10)

here η is a learning constant. The amplitudes asso-

ciated with the other terms of the Fourier series are

determined by

= ηcos(iφ) · e, (11)

= ηsin(iφ) · e, (12)

where i = 1...M. As shown in Figure 3, the oscillator

of the feedback structure receives the difference be-

tween the input signal and the Fourier series. Since

a negative feedback loop is used, the difference ap-

proaches zero when the Fourier series representation

approaches the input signal. Such a feedback struc-

ture preforms an adaptive Fourier analysis, where the

phase difference between the harmonics can only be

0, π/2, π or 3π/2. This is not the case in the origi-

nal approach (Righetti and Ijspeert, 2006), where the

phase difference can be arbitrary.

The proposed approach has the ability to adapt to

the basic frequencyof the input signal. The number of

harmonic frequency components it can accurately ex-

tract depends on how many terms of the Fourier series

are used. Since in this structure only one oscillator is

used and the harmonics are encoded in the Fourier

series, the basic frequency and phase are clearly de-

ﬁned. This is an important improvement, especially

for the usefulness of the imitation system when per-

forming rhythmic tasks.

The new architecture of the canonical dynamic

system can be used as an imitation system by itself,

as it is able to learn arbitrary periodic signals. Af-

ter convergence, e reaches zero (with an accuracy that

depends on the number of elements of the Fourier se-

ries). Once e is zero, the periodic signal stays encoded

in the Fourier series. The learning process is embed-

ded and is done in real-time. There is no need for any

external optimization process or learning algorithm.

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

Adding the output dynamical system enables us to

synchronise the motion of the robot to a measurable

periodic quantity of the task we would like to preform.

The measured signal is now encoded into the Fourier

series and the desired robot trajectory is encoded in

the output dynamic system. Sice adaptation of the

frequency and the learning of the desired trajectory

can be done simultaneously, all of the system time-

delays can be automatically included. Furthermore,

when a predeﬁned motion pattern for the trajectory

is used, the system time-delays can be adjusted with

a phase lag parameter φ

. This enables us to either

predeﬁne the desired motion or to teach the robot how

to preform the desired rhythmic task online.

The output dynamical system also ensures greater

robustness against perturbations and smooth modula-

tion. Specially greater robustness to perturbation is

crucial when performing fast, dynamic tasks.

4 EVALUATION

In the following section we evaluate of the proposed

imitation system with the new canonical dynamical

layer. In the Section 4.1 the numerical results from

the original and the novel architectures are presented.

In Section 4.2 a real-world experiment of playing the

yo-yo with the use of the proposed imitation system

is shown.

4.1 Simulation

In this numerical experiment the proposed architec-

ture for the canonical dynamical system learns an ar-

bitrary signal. The populating of the frequency spec-

trum is done without any signal processing, as the

whole process of frequency extraction and adaptation

of the waveform is completely embedded in the dy-

namics of the adaptive frequency oscillator combined

with the adaptive Fourier series. Unless stated other-

wise, we use the following parameters: µ = 2, K = 20,

M = 10.

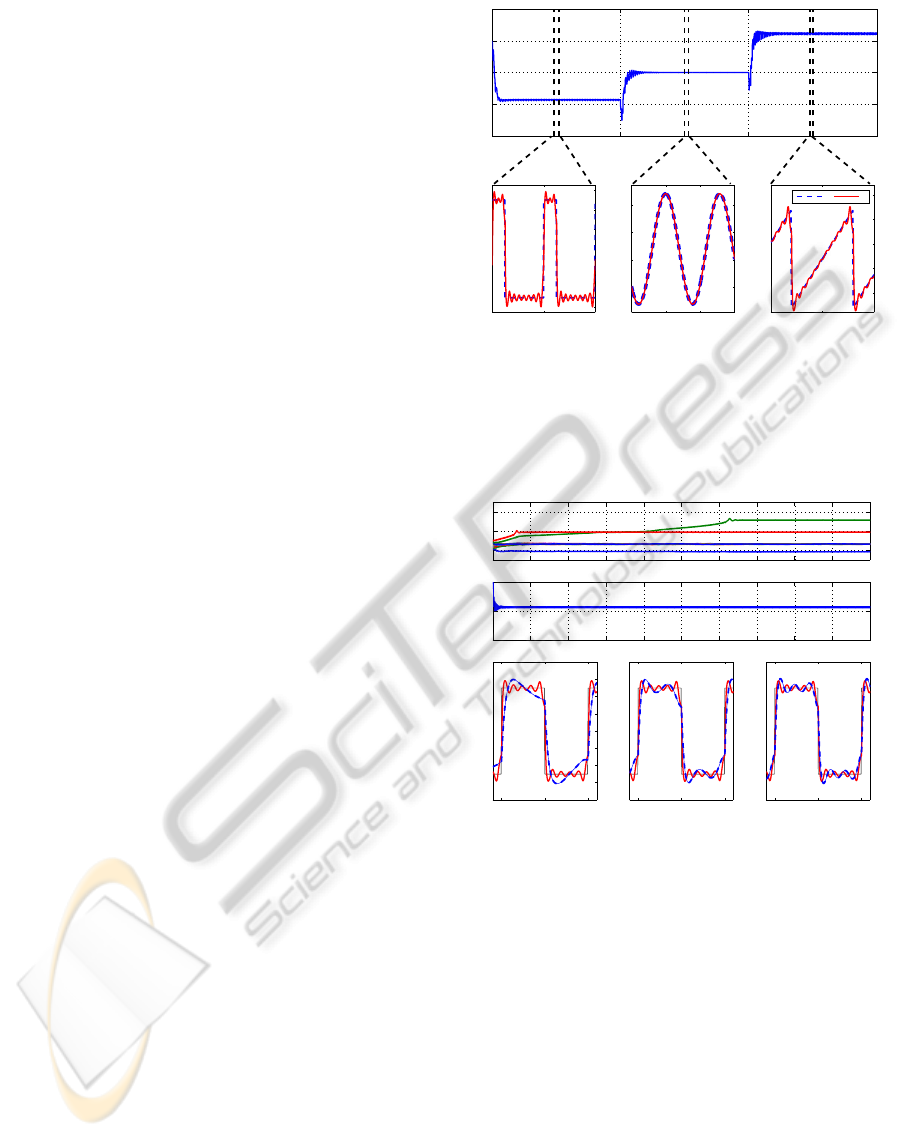
Frequency adaptation results from time- and

shape-varying signals are illustrated in Figure 4. The

input signal itself is of three parts: a periodic pulse

signal, a sinusoid, and a sawtooth wave signal. Tran-

sition between the signal parts is instant for both fre-

quency and waveform. We can see that after the

change of the input signal, the output frequency sta-

bilises very quickly.

A single adaptive frequency oscillator in a feed-

back loop is enough, because the harmonics of the

input signal are encoded with the Fourier series in

the feedback loop. As can be seen from the bottom

0 50 100 150

24 25 26

−0.4

−0.2

0.2

0.4

0.6

0.8

75 75.5 76 76.5

−1

−0.5

0.5

124 124.5 125

−1

−0.5

0.5

ˆy

Time [s]

Ω rad/s

Figure 4: Typical convergence of an adaptive frequency os-

cillator combined with an adaptive Fourier series, driven by

a periodic signal with different waveforms and frequencies.

Frequency adaptation is presented in the top plot and the

comparison between the input signal y and the approxima-

tion ˆy in the bottom plot.

0 50 100 150 200 250 300 350 400 450 500

20 20.5 21

−0.8

−0.6

−0.4

−0.2

0.2

0.4

0.6

150 150.5 151 350 350.5 351

Time [s]

Ω rad/s Ω rad/s

Figure 5: Comparison between the pool of the adaptive os-

cillators and our proposed approach. First plot shows evolu-

tion of frequency distribution using a pool of 10 oscillators.

Middle plot shows the extracted frequency using an adap-

tive frequency oscillator combined with Fourier seres. The

comparison of approximated signals is presented in the bot-

tom plot. The thin solid line presents the input signal, the

solid line presents our new proposed approach and the dot-

ted line presents the pool of adaptive oscillators.

plots in Figure 4, the input signal and the feedback

signal are very well matched. The approximation er-

ror depends only on M. A comparison with the orig-

inal approach as proposed in (Buchli et al., 2008) is

given in Figure 5. In their approach, if there are not

enough oscillators to encode the input signal, the sys-

tem will only learn the frequency components with

more power. Thus, the output signal will only be an

approximation.

FREQUENCY EXTRACTION BASED ON ADAPTIVE FOURIER SERIES - Application to Robotic Yoyo

Mitsubishi PA-10

Force sensor

Gripper

Camera

Line

Yo-yo

Figure 6: Experimental setup.

Canonic

dynamic

system

Output

dynamic

system

yoyo

Ω

Figure 7: Proposed two-layered structure of the control sys-

tem for controlling the peak height of the yo-yo. The input

is either the force y

or the visual feedback y

However, if there are more oscillators than the fre-

quency components to learn, either some of them will

not converge to any frequency or the same frequency

components will be coded by several oscillators, as

shown in the top plot in Figure 5, where a pool of ten

oscillators was used. In this particular experiment,

ﬁve of the oscillators converge to the basic frequency

of the signal.

Choosing the right oscillator from that pool is a

very difﬁcult task and requires a complex logic algo-

rithm. On the other hand, using our new approach,

where the feedback is encoded with a Fourier series,

the oscillator converges to the basic frequency of the

input signal. Therefore, the basic frequency and the

phase are clearly deﬁned. Furthermore, the approx-

imation and the convergence of the feedback signal

is quicker, as it is shown in the bottom plots in Fig-

ure 5. Even after 350 s, the original architecture from

(Righetti and Ijspeert, 2006) did not produce as good

an approximation as it was after 20 s when using our

new proposed canonical dynamical system.

4.2 Application to Robotic Yo-yo

To illustrate the proposed approach we implemented

it on a real robot playing yo-yo.

Playing yo-yo with a robot can be achieved in dif-

ferent ways, depending on what one can measure. It

can be the length of the unwound string, which can

be effectively measured by a vison system. As de-

scribed in (

Zlajpah, 2006), using vison is also one of

the ways humans do it, even though approaches us-

ing only the measured force were described (Jin et al.,

2009). With our proposed system, playing yo-yo can

be accomplished either with force feedback or with

visual feedback. Furthermore, the proposed system is

able to synchronise even if the input signal is changed

from one measurable quantity to another during the

experiment.

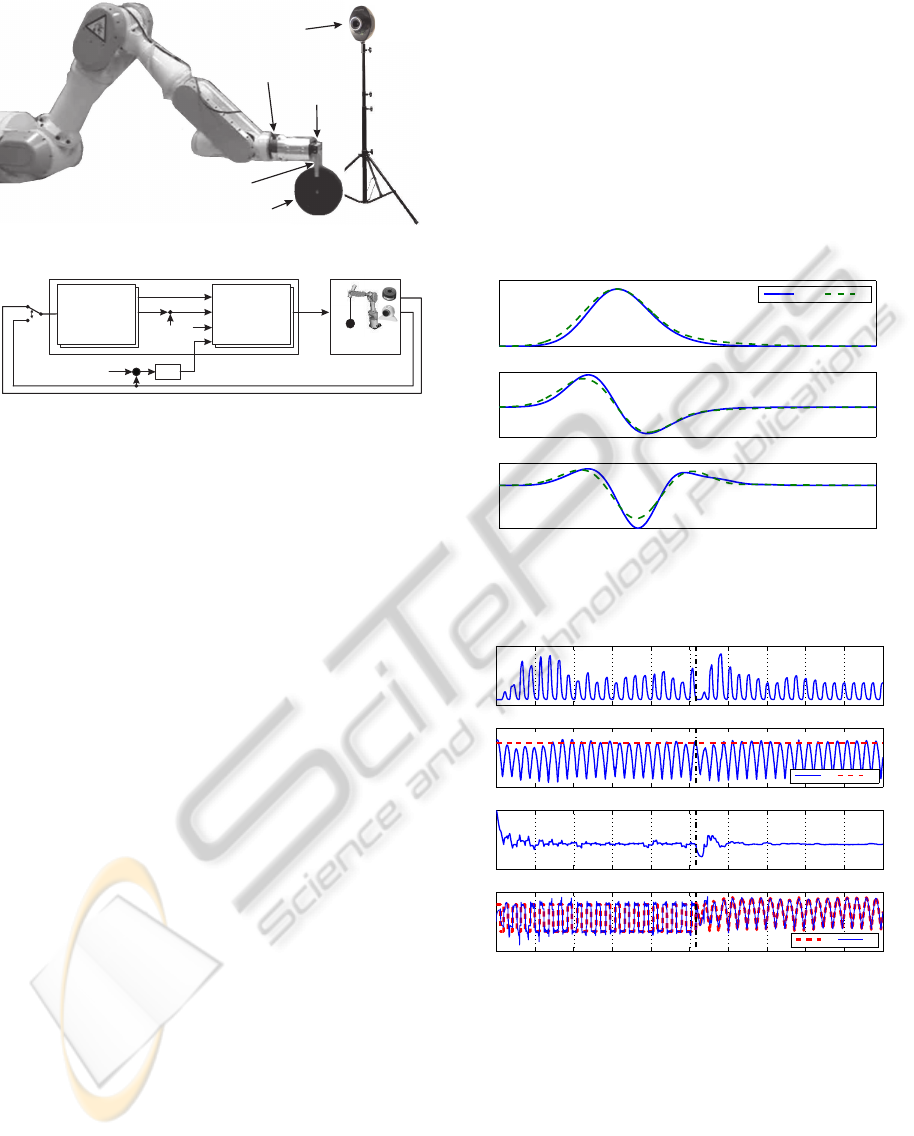
We preformed the experiment on a Mitsubishi PA-

10 robot as presented in Figure 6. A force sensor

(JR3), was attached to the end effector to measure the

impact force of the yoyo, and a USB camera was used

to measure the length of the unwound string.

ref

0 1

t [s]

Figure 8: Pre-deﬁned hand motion pattern for playing yo-

yo.

0.5

−0.8

0.2

0 10 20 30 40 50 60 70 80 90 100

−0.6

0.6

ˆy

Time [s]

Ω [rad/s]

x [m]

h [m]

Figure 9: Robot trajectory x in the top plot, height h of the

yo-yo in the second plot, extracted frequency in the third

plot and signal adaptation ˆy in the bottom plot. At 52 s

the input signal is switched form force feedback to visual

feedback. Yo-yo parameters in this case are: axle radius

= 0.01 m and mass m = 0.2564 kg.

The two layered imitation system with the novel

canonical dynamical system was implemented in

Matlab/Simulik. The control scheme is presented

in Figure 7. As we can see, the imitation system,

based on a nonlinear oscillator combined with dy-

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics

0 s

0.32 s

0.64 s

0.96 s

1.28 s

1.6 s

1.92 s

2.24 s

+ 0.32 s

+ 0.64 s

+ 0.96 s

+ 1.28 s

+ 1.6 s

+ 1.92 s

+ 2.24 s

+ 0.32 s

+ 0.64 s

+ 0.96 s

+ 1.28 s

+ 1.6 s

+ 1.92 s

+ 2.24 s

Figure 10: Image sequence of a robotic yoyo. Top sequence present the decent of the yoyo from the gripper. In the middle

sequence a behavior of the system after switching from force feedback to vision feedback is shown (t

= 54 s) and in bottom

sequence the behavior in steady state is presented (t

= 81 s).

namic Fourier series, provides the desired trajectory

for the robot with a yo-yo attached at the top. The mo-

tion of the robot was constrained to up-down motion

using inverse kinematics. The length of the string or

the force from the top of the robot can be used as the

input into the system. Since a measurable force dif-

ference appears only as a spike, when the yo-yo hits

the end of the string, we modify the signal in a way

that it carries more energy. In our particular case, we

use the measured spike to create a short pulse.

To preform the task, we ﬁrst determine the wave-

form of the required motion pattern. We chose the

motion pattern described in (

Zlajpah, 2006), which

satisﬁes the required criteria for playing the yo-yo.

The hand motion pattern encoded into the output dy-

namic system (dashed line), and the desired hand mo-

tion pattern (solid line) are presented in Figure8.

The frequency of the task depends on the param-

eters of the yo-yo itself, and on how high the yo-yo

rolls up along the string. The height can be inﬂu-

enced by the amplitude of the hand motion, which can

be easily modiﬁed using the amplitude parameter r of

the motion, see Figure 7. PI controller was used to

control the peak height of the yo-yo. The controller is

given by

u(t) = k

e(t) + k

e(t)dt, (13)

where k

= 2, and k

= 0.4 were determined empiri-

cally. Figure 9 shows the results of frequency adapta-

tion and yo-yo height during the experiment.

As we can see, the frequency of the imitated mo-

tion quickly adapted to the motion of the yo-yo and

stable motion was achieved. At approximately 52 s

the input into the imitation system was switched from

force feedback to visual feedback. At that point some

oscillation in the frequency and the approximation of

the input signal can be observed because they have to

adapt to the new waveform of the input signal. Fur-

thermore, form the middle sequence in Figure 10 we

can see that the amplitude of hand motion is higher

after switching from the force feedback to the vision

feedback. Despite the change, the imitation system

still manages to extract the correct frequency and the

robot motion returns to steady-state oscillations. Note

that in the bottom sequence in Figure 10 the hand am-

plitude is smaller than immediately after the switch.

FREQUENCY EXTRACTION BASED ON ADAPTIVE FOURIER SERIES - Application to Robotic Yoyo

As far as we know, this is the ﬁrst system which

has the capability of playing the yo-yo by force feed-

back or by vision feedback, without changing the sys-

tem parameters. Furthermore, switching from one to

another measured quantity can even be done during

the experiment. This shows that the proposed system

is adaptable and robust.

5 CONCLUSIONS

We presented a new architecture for the canonical dy-

namical system which is a part of a two layered imi-

tation system, but can be used as an imitation system

by itself. The dynamical system which, is used to ex-

tract the frequency, is composed of a nonlinear phase

oscillator combined with a Fourier series. This sys-

tem essentially implements an adaptive Fourier series

of the input signal. It can extract the frequency, phase

and the Fourier series coefﬁcients of an unknown pe-

riodic signal. This is done in real-time without any

additional processing of the input signal. Integrating

this system into the imitation system based on dy-

namic motion primitives enables simple and compu-

tationally inexpensive control of rhythmic tasks with

at least one measurable periodic quantity.

Furthermore, we presented the use of the imita-

tion system to preform a rhythmic task that requires

synchronization with the controlled device. For play-

ing the yo-yo, we have shown that the information

on how high the yo-yo rolls up along the string, or

the force feedback is enough to achieve stable perfor-

mance. The proposed approach enables to play yo-yo

by measuring either the force or the yo-yo position.

Furthermore we also showed that the system has the

capability of changing the measured quantity in a sin-

gle experiment without loosing the synchronization

between the robot and the yo-yo.

REFERENCES

Buchli, J. and Ijspeert, A. (2004). A simple, adaptive loco-

motion toy-system. In Schaal, S., Ijspeert, A., Billard,

A., Vijayakumar, S., Hallam, J., and Meyer, J., editors,

From Animals to Animats 8. Proceedings of the Eighth

International Conference on the Simulation of Adap-

tive Behavior (SAB’04), pages 153–162. MIT Press.

Buchli, J., Righetti, L., and Ijspeert, A. J. (2008). Frequency

Analysis with coupled nonlinear Oscillators. Physica

D: Nonlinear Phenomena, 237:1705–1718.

Degallier, S., Righetti, L., Natale, L., Nori, F., Metta, G.,

and Ijspeert, A. (2008). A modular bio-inspired ar-

chitecture for movement generation for the infant-

like robot iCub. In Proceedings of the 2nd IEEE

RAS / EMBS International Conference on Biomedical

Robotics and Biomechatronics (BioRob).

Gams, A., Ijspeert, A. J., Schaal, S., and Lenarcic, J.

(2009). On-line learning and modulation of periodic

movements with nonlinear dynamical systems. Auton.

Robots, 27(1):3–23.

Gams, A.,

Zlajpah, L., and Lenarˇciˇc, J. (2007). Imitating

human acceleration of a gyroscopic device. Robotica,

25(4):501–509.

Ijspeert, A. J. (2008). Central pattern generators for loco-

motion control in animals and robots: A review. Neu-

ral Networks, 21(4):642–653.

Jin, H.-L., Ye, Q., and Zacksenhouse, M. (2009). Return

maps, parameterization, and cycle-wise planning of

yo-yo playing. Trans. Rob., 25(2):438–445.

Kasuga, T. and Hashimoto, M. (2005). Human-robot hand-

shaking using neural oscillators. In ICRA, pages

3802–3807.

Matsuoka, K., Ohyama, N., Watanabe, A., and Ooshima, M.

(2005). Control of a giant swing robot using a neural

oscillator. In ICNC (2), pages 274–282.

Petriˇc, T., Gams, A., and

Zlajpah, L. (2009). Modeling

and control strategy for robotic powerball. In RAAD,

page 7.

Righetti, L., Buchli, J., and Ijspeert, A. J. (2006). Dy-

namic hebbian learning in adaptive frequency oscil-

lators. Physica D, 216(2):269–281.

Righetti, L. and Ijspeert, A. J. (2006). Programmable Cen-

tral Pattern Generators: an application to biped loco-

motion control. In Proceedings of the 2006 IEEE In-

ternational Conference on Robotics and Automation.

Schaal, S. (1999). Is imitation learning the route to hu-

manoid robots? Trends in cognitive sciences, 6:233–

242.

Schaal, S., Mohajerian, P., and Ijspeert, A. (2007). Dy-

namics systems vs. optimal control–a unifying view.

Progress in Brain Research, 165:425–445.

Ude, A., Atkeson, C. G., and Riley, M. (2000). Planning of

joint trajectories for humanoid robots using b-spline

wavelets. In ICRA, pages 2223–2228.

Zlajpah, L. (2006). Robotic yo-yo: modelling and control

strategies. Robotica, 24(2):211–220.

ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics