DESIGN OF ALLPASS FILTERS WITH SPECIFIED DEGREES OF
FLATNESS AND EQUIRIPPLE PHASE RESPONSES
Xi Zhang
Department of Information and Communication Engineering, The University of Electro-Communications
1–5–1 Chofugaoka, Chofu-shi, 182-8585, Tokyo, Japan
Keywords:
IIR allpass filter, Flatness, Equiripple approximation, Remez exchange algorithm.
Abstract:
This paper proposes a new method for designing allpass filters having the specified degrees of flatness at the
specified frequency point(s) and equiripple phase responses in the approximation band(s). First, a system of
linear equations are derived from the flatness conditions. Then, the Remez exchange algorithm is used to
approximate the equiripple phase responses in the approximation band(s). By incorporating the linear equa-
tions from the flatness conditions into the equiripple approximation, the design problem is formulated as a
generalized eigenvalue problem. Therefore, we can solve the eigenvalue problem to obtain the filter coeffi-
cients, which have the equiripple phase response and satisfy the specified degrees of flatness simultaneously.
Furthermore, a class of IIR filters composed of allpass filters are introduced as one of its applications, and it is
shown that IIR filters with flat passband (or stopband) and equiripple stopband (or passband) can be designed
by using the proposed method. Finally, some examples are presented to demonstrate the effectiveness of the
proposed design method.
1 INTRODUCTION
Allpass filters possess constant magnitude response at
all frequencies and are a basic scalar lossless building
block (Mitra and Kaiser, 1993), (Regalia et al., 1988).
Interconnections of allpass filters have found numer-
ous applications in many practical filtering problems
such as low-sensitivity filter structures, wavelet filter
banks, and so on (Mitra and Kaiser, 1993), (Shenoi,
1999), (Regalia et al., 1988), (Laakso et al., 1996),
(Lang, 1998), (Selesnick and Burrus, 1998), (Se-
lesnick, 1999), (Zhang and Iwakura, 1999). In many
applications, it is necessary to design an allpass fil-
ter both satisfying the specified degrees of flatness at
the specified frequency point(s) and having equiripple
phase response in the approximation band(s). For ex-
ample, in the allpass-sum structure (Selesnick, 1999),
the phase response of the allpass sub-filter is required
to be flat in the band(s) where the corresponding fil-
ter has the flat magnitude response, and is equiripple
in other band(s) to get the equiripple magnitude re-
sponse. Many methods have been proposed for the
phase design of allpass filters: the maximally flat
design (Thiran, 1971), least squares design (Laakso
et al., 1996), (Lang, 1998), and equiripple design
(Zhang and Iwakura, 1999), (Tseng, 2003).
However, the approximation of allpass filters with
both the specified degrees of flatness and equiripple
phase responses in the approximation band(s) is still
open.
In this paper, we propose a new method for de-
signing allpass filters which have both the specified
degrees of flatness at the specified frequency point(s)
and equiripple phase responses in the approximation
band(s). First, we derive a system of linear equations
from the flatness conditions of the phase response at
the specified frequency point(s). Then, we apply the
Remez exchange algorithm to obtain the equiripple
reponse in the approximation band(s). By incorpo-
rating the linear equations from the flatness condi-
tions into the equiripple approximation, we formulate
the design problem as a generalized eigenvalue prob-
lem (Zhang and Iwakura, 1996), (Zhang and Iwakura,
1999). Therefore, we can obtain the filter coefficients
by iteratively solving the eigenvalue problem. The
resulting allpass filters have the equiripple phase re-
sponses and satisfy the specified degrees of flatness si-
multaneously. Furthermore, as one of the applications
of allpass filters, we introduce a class of IIR filters
composed of allpass filters (Regalia et al., 1988), (Se-
lesnick, 1999), whose design problem can be reduced
to the phase approximation of the allpass sub-filter.
205
Zhang X. (2010).
DESIGN OF ALLPASS FILTERSWITH SPECIFIED DEGREES OF FLATNESS AND EQUIRIPPLE PHASE RESPONSES.
In Proceedings of the International Conference on Signal Processing and Multimedia Applications, pages 205-210
DOI: 10.5220/0002934102050210
Copyright
c
 SciTePress

Thus, we can design the filters with flat passband (or
stopband) and equiripple stopband (or passband) by
using the proposed method. Finally, some design ex-
amples are presented to demonstrate the effectiveness
of the proposed design method.
2 ALLPASS FILTERS
It is well-known that the transfer function of an all-
pass filter A(z) is defined by
A(z) = z
−N
N
∑
n=0
a
n
z
n
N
∑
n=0
a
n
z
−n
, (1)
where N (∈ Z) is filter degree, and a
n
(∈ R) are real
coefficients and a
0
= 1.
It can be seen that A(z) in Eq.(1) has unit mag-
nitude response at all frequencies, and its phase re-
sponse θ(ω) is given by
θ(ω) = −Nω + 2tan
−1
N
∑
n=0
a
n
sinnω
N
∑
n=0
a
n
cosnω
. (2)
Let θ
d
(ω) be the desired phase response. The dif-
ference θ
e
(ω) between θ(ω) and θ
d
(ω) is
e
jθ
e
(ω)
= e
j{θ(ω)−θ
d
(ω)}
=
N
∑
n=0
a
n
e
j{(n−
N
2
)ω−
θ
d
(ω)
2
}
N
∑
n=0
a
n
e
− j{(n−
N
2
)ω−
θ
d
(ω)
2
}
,
(3)
and
θ
e
(ω) = 2tan
−1
N
∑
n=0
a
n
sin{(n−
N
2
)ω−
θ
d
(ω)
2
}
N
∑
n=0
a
n
cos{(n−
N
2
)ω−
θ
d
(ω)
2
}
.
(4)
Therefore, the design problem of allpass filters
is the phase approximation of θ(ω) to θ
d
(ω) in the
approximation band(s), that is, the minimization of
the phase error θ
e
(ω) in Eq.(4) in the specified cri-
terion, e.g., in the least squares, and/or Chebyshev
(minimax), and/or maximally flat sense. In the fol-
lowing, we discuss the design of allpass filters hav-
ing equiripple phase responses in the approximation
band(s) while satisfying the specified degrees of flat-
ness at the specified frequency point(s).
3 ALLPASS FILTER DESIGN
In this section, we describe the design method of all-
pass filters with both the specified degrees of flatness
and equiripple phase responses in the approximation
band(s). Firstly, we consider the flatness condition of
the phase response at the frequency point ω
p
. It is re-
quired that the derivatives of θ(ω) in Eq.(2) are equal
to that of θ
d
(ω) at ω = ω
p
, that is,
∂
r
θ(ω)
∂ω
r




ω=ω
p
=
∂
r
θ
d
(ω)
∂ω
r




ω=ω
p
(r = 0, 1, ··· , K − 1),
(5)
where K (∈ Z) is a parameter that controls the degree
of flatness. It is seen that to satisfy the specified de-
grees of flatness, the flatness conditions in Eq.(5) be-
come
∂
r
θ
e
(ω)
∂ω
r




ω=ω
p
= 0 (r = 0, 1, ··· , K − 1). (6)
From Eq.(4), we have
tan
θ
e
(ω)
2
=
N(ω)
D(ω)
, (7)
where











N(ω) =
N
∑
n=0
a
n
sin{(n−
N
2
)ω−
θ
d
(ω)
2
}
D(ω) =
N
∑
n=0
a
n
cos{(n−
N
2
)ω−
θ
d
(ω)
2
}
. (8)
Therefore, it is proven that the condition in Eq.(6) is
equivalent to
∂
r
N(ω)
∂ω
r




ω=ω
p
= 0 (r = 0, 1, ··· , K − 1). (9)
By substituting N(ω) in Eq.(8) into Eq.(9), we can
derive a system of linear equations as follows,
N
∑
n=0
∂
r
sin{(n−
N
2
)ω−
θ
d
(ω)
2
}
∂ω
r




ω=ω
p
a
n
= 0, (10)
for r = 0, 1, ··· , K − 1. For example, if a linear phase
is required, that is, θ
d
(ω) = −τω, then Eq.(10) is re-
duced to
SIGMAP 2010 - International Conference on Signal Processing and Multimedia Applications
206








N
∑
n=0
(n−
N−τ
2
)
r
sin{(n−
N−τ
2
)ω
p
}a
n
= 0 (even r)
N
∑
n=0
(n−
N−τ
2
)
r
cos{(n−
N−τ
2
)ω
p
}a
n
= 0 (odd r)
.
(11)
It is known that the phase response θ(ω) is an odd
function with respect to ω = 0 and π. If ω
p
= 0 or π,
then the equations with even r are satisfied without
any conditions, and thus the number of the condi-
tions reduces about a half, that is, L = ⌊
K
2
⌋, where ⌊x⌋
means the largest integer not greater than x. When
ω
p
6= 0 and π, then L = K.
When the above-mentioned conditions are im-
posed at several frequency points ω
pi
(i = 1, 2, ··· ,
M), the total number of the conditions is L =
∑
M
i=1
L
i
,
where L
i
= ⌊
K
i
2
⌋ if ω
pi
= 0 or π, and L
i
= K
i
if
ω
pi
6= 0 and π. Note that K
i
is a parameter that con-
trols the degree of flatness at ω
pi
. Therefore, if L = N,
we can solve a system of linear equations as shown
in Eq.(10) to obtain a set of filter coefficients, which
has the maximally flat phase response and satisfies the
specified degrees of flatness at the specified frequency
point(s) ω
pi
.
Next, we consider the case of L < N. Besides sat-
isfying the flatness conditions in Eq.(5), we want to
obtain an equiripple phase response in the approxi-
mation band(s) by using the remaining degree of free-
dom. We apply the Remez exchange algorithm in the
approximation band(s). Let ω
i
(i = 0, 1, ··· , N − L)
are the extremal frequencies in the approximation
band(s), we formulate θ
e
(ω) as
tan
θ
e
(ω
i
)
2
=
N
∑
n=0
a
n
sin{(n−
N
2
)ω
i
−
θ
d
(ω
i
)
2
}
N
∑
n=0
a
n
cos{(n−
N
2
)ω
i
−
θ
d
(ω
i
)
2
}
= (−1)
i
δ,
(12)
where δ (∈ R) is an error. We incorporate Eq.(10) into
Eq.(12), and formulate the design problem as a gener-
alized eigenvalue problem. Then we rewrite Eqs.(10)
and (12) in the matrix form as
PA = δQA, (13)
where A = [a
0
, a
1
, ··· , a
N
]
T
, and the elements of the
matrices P and Q, for example, when the flatness
condition in Eq.(5) is imposed at only one frequency
0 0.1 0.2 0.3 0.4 0.5
−8
−6
−4
−2
0
NORMALIZED FREQUENCY
PHASE RESPONSE ( )
K=7
K=9
K=11
π
Figure 1: Phase responses of allpass filters.
point ω
p
(6= 0 and π), are given by
P
ij
=



















∂
i
sin{( j −
N
2
)ω−
θ
d
(ω)
2
}
∂ω
i




ω=ω
p
(i = 0, 1, ··· , L− 1)
sin{( j −
N
2
)ω
(i−L)
−
θ
d
(ω
(i−L)
)
2
}
(i = L, L+ 1, ··· , N)
,
(14)
Q
ij
=







0 (i = 0, 1, ··· , L− 1)
(−1)
(i−L)
cos{( j −
N
2
)ω
(i−L)
−
θ
d
(ω
(i−L)
)
2
}
(i = L, L+ 1, ··· , N)
.
(15)
Once the design specification: the filter degree N,
the desired phase response θ
d
(ω), the degree of flat-
ness K
i
, the specified frequency point(s) ω
pi
, and the
extremal frequencies ω
i
in the approximation band(s)
are given, the elements P
ij
and Q
ij
of the matrices P
and Q can be computed by Eqs.(14) and (15). There-
fore, it should be noted that Eq.(13) corresponds to
a generalized eigenvalue problem, i.e., δ is an eigen-
value, and A is a corresponding eigenvector. In or-
der to minimize the error δ, we must find the absolute
minimum eigenvalue by solving the eigenvalue prob-
lem, so that the corresponding eigenvector gives a set
of filter coefficients a
n
. To obtain an equiripple phase
response, we make use of an iteration procedure so
that the optimal filter coefficients is easily obtained.
The design algorithm is shown as follows.
DESIGN OF ALLPASS FILTERSWITH SPECIFIED DEGREES OF FLATNESS AND EQUIRIPPLE PHASE
RESPONSES
207

4 DESIGN ALGORITHM
Procedure. {Allpass Filter Design Algorithm.}
Begin
1) Read N, θ
d
(ω), K
i
, and ω
pi
.
2) Select initial extremal frequencies Ω
i
(i =
0, 1, ··· , N − L) equally spaced in approximation
band(s).
Repeat
3) Set ω
i
= Ω
i
(i = 0, 1, · · · , N − L).
4) Compute P and Q by using Eqs.(14) and (15), and
find the absolute minimum eigenvalue δ to obtain
a set of filter coefficients a
n
.
5) Search the peak frequencies Ω
i
(i = 0, 1, · · · , N −
L) of θ
e
(ω) in approximation band(s).
Until
Satisfy the following condition for a prescribed small
constant ε (for example, ε = 10
−8
):
|ω
i
− Ω
i
| < ε (for all i)
End.
5 IIR FILTERS COMPOSED OF
ALLPASS FILTERS
Many methods for designing IIR filters have been pro-
posed in (Mitra and Kaiser, 1993), (Regalia et al.,
1988), (Zhang and Iwakura, 1996), (Lang, 1998),
(Hegde and Shenoi, 1998), (Selesnick and Burrus,
1998), (Selesnick, 1999). These design methods have
considered the maximally flat and/or equiripple mag-
nitude responses. It is required in some applications
that the magnitude response of the filters is flat in
passband(s) and equiripple in stopband(s) (Darling-
ton, 1978), (Vaidyanathan, 1985), (Selesnick and Bur-
rus, 1996), (Hegde and Shenoi, 1998). In this section,
we discuss the design of IIR filters with flat pass-
band(s) and equiripple stopband(s), which are com-
posed of two allpass filters.
It is known in (Regalia et al., 1988), (Lang, 1998),
(Selesnick and Burrus, 1998) and (Selesnick, 1999)
that a parallel interconnection of two allpass filters
(allpass-sum) has many advantages, such as low-
sensitivity structures, low-complexity structures with
low roundoff noise behavior, and so on. The classical
digital (Butterworth, Chebyshev, and elliptic) filters
can be realized as an allpass-sum structure. In addi-
tion, the allpass-sum structure can realize a more gen-
eral class of transfer functions. Here, we consider this
class of IIR filters whose transfer function is given by
H(z) =
1
2
[z
−J
A
1
(z) + A
2
(z)], (16)
0 0.1 0.2 0.3 0.4 0.5
−0.1
−0.05
0
0.05
0.1
NORMALIZED FREQUENCY
PHASE ERROR ( )
K=7
K=9
K=11
π
Figure 2: Phase errors of allpass filters.
where A
1
(z), A
2
(z) are two causal stable allpass filters
of degree N
1
, N
2
, and J (∈ Z) is a nonnegative integer.
Eq.(16) can be rewritten to
H(z) =
1
2
A
1
(z)[z
−J
+ A(z)], (17)
where
A(z) =
A
2
(z)
A
1
(z)
, (18)
whose degree is N = N
1
+ N
2
. Note that A(z) needs
not be causal stable. The magnitude response of H(z)
is given by
|H(e
jω
)| = |cos
θ(ω) + Jω
2
|, (19)
where θ(ω) is the phase response of A(z). It is clear
that the phase difference between A(z) and z
−J
must
be 2nπ in the passband(s) of H(z), and (2n + 1)π in
the stopband(s), where n ∈ Z. Therefore, the desired
phase response of A(z) is
θ
d
(ω) =

−Jω+ 2nπ (in passband)
−Jω+ (2n+ 1)π (in stopband)
,
(20)
then the design problem of H(z) becomes the phase
approximation of A(z). The conventional design
methods, for example, the maximally flat design (Thi-
ran, 1971), equiripple design (Zhang and Iwakura,
1999), (Tseng, 2003) and so on, can be used in the
design. However, these methods cannot design all-
pass filters with flat and equiripple phase response in
passband(s) and stopband(s), respectively. By using
the design method proposed in the preceding section,
we can obtain easily the flat passband(s) and equirip-
ple stopband(s) of H(z).
SIGMAP 2010 - International Conference on Signal Processing and Multimedia Applications
208

0 0.1 0.2 0.3 0.4 0.5
−80
−60
−40
−20
0
NORMALIZED FREQUENCY
MAGNITUDE RESPONSE (dB)
K=7
K=9
K=11
Figure 3: Magnitude responses of IIR lowpass filters.
For example, if we want H(z) to be a lowpass fil-
ter, the desired phase response is given by
θ
d
(ω) =

−Jω (0 ≤ ω ≤ ω
1
)
−Jω± π (ω
2
≤ ω ≤ π)
, (21)
where ω
1
and ω
2
are the cutoff frequencies of the
passband and stopband, respectively. Note that in
this case, the filter degrees N
1
and N
2
must satisfy
N
2
− N
1
= J ∓ 1. If we set N
1
= 0 and N = N
2
=
J ∓1, then the filter will have an approximately linear
phase response also (Laakso et al., 1996), (Zhang and
Iwakura, 1999).
We use the proposed method to design the allpass
filter A(z), whose phase response θ(ω) satisfies Eq.(5)
at ω
p
= 0. Note that K should be an odd number, be-
cause θ(ω) is an odd function with respect to ω = 0.
Thus, the resulting lowpass filter H(z) has a flat mag-
nitude response at ω
p
= 0, and the degree of flatness
is 2K.
6 DESIGN EXAMPLES
In this section, we present some examples to
demonstrate the effectiveness of the proposed design
method.
First, we consider the design of allpass filter of de-
gree N = 8 with the desired phase response θ
d
(ω) =
−7ω in [0, 0.3π] and θ
d
(ω) = −7ω − π in [0.5π, π].
The degree of flatness is required to be K = 9 at
ω
p
= 0, then L = 4. Since the remaining degree of
freedom is N − L = 4, we have selected initial ex-
tremal frequencies 0.5π = ω
0
< ω
1
< ·· · < ω
4
< π
equally spaced in [0.5π, π], and obtained the optimal
0 0.1 0.2 0.3 0.4 0.5
−8
−6
−4
−2
0
NORMALIZED FREQUENCY
PHASE RESPONSE ( )
K=7
K=9
K=11
π
Figure 4: Phase responses of IIR lowpass filters.
filter coefficients a
n
by using the design algorithm de-
scribed in the section IV. The resulting phase response
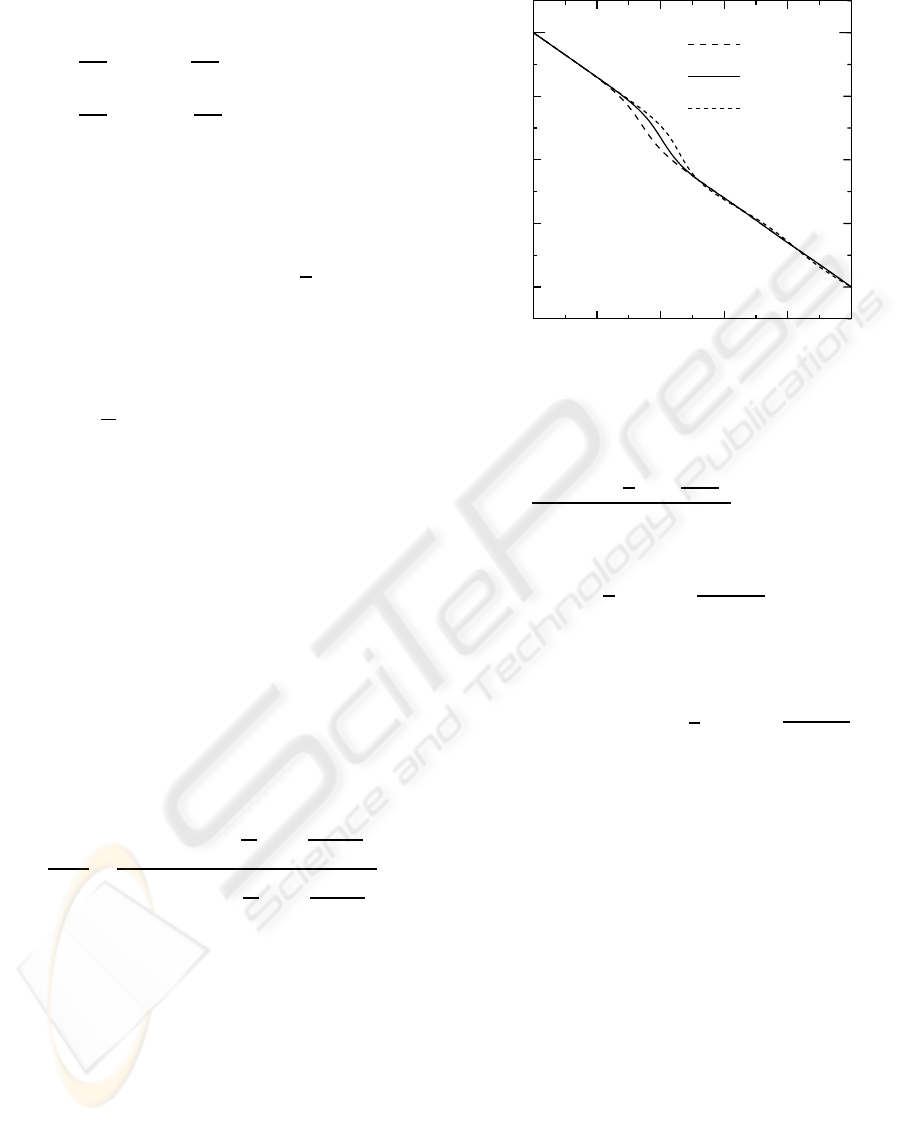
and phase error are shown in the solid line in Fig.1 and
Fig.2, respectively. It is clear in Fig.2 that the phase
response is flat at ω = 0 and equiripple in [0.5π, π]. In
Fig.1 and Fig.2, the phase responses of two allpass fil-
ters with K = 7 and K = 11 are shown also. It is seen
that the degree of flatness K can be arbitrarily spec-
ified. It is found that these allpass filters are causal
stable since all poles are within the unit circle (Zhang
and Iwakura, 1999).
Next, we use the obtained allpass filters to con-
struct IIR lowpass filters: H(z) =
1
2
[z
−7
+ A(z)]. The
magnitude and phase responses of the IIR filters are
shown in Fig.3 and Fig.4, respectively. It is seen in
Fig.3 and Fig.4 that these lowpass filters have the flat
passband and equiripple stopband responses, while
the phase responses are approximately linear.
7 CONCLUSIONS
In this paper, we have proposed a new method for de-
signing allpass filters which have both the specified
degrees of flatness and equiripple phase responses
in the approximation band(s). Firstly, a system of
linear equations have been derived from the flatness
conditions of the phase responses, then the Remez
exchange algorithm is used to get the equiripple re-
sponses in the approximation band(s). The design
problem has been formulated as a generalized eigen-
value problem by incorporating the flatness condi-
tions into the equiripple approximation, thus, a set of
filter coefficients can be easily obtained by solving the
eigenvalue problem. Furthermore, as one application
DESIGN OF ALLPASS FILTERSWITH SPECIFIED DEGREES OF FLATNESS AND EQUIRIPPLE PHASE
RESPONSES
209

of allpass filters, a class of IIR filters composed of two
allpass filters has been discussed also. Finally, some
examples have been presented to demonstrate the ef-
fectiveness of the proposed design method.
REFERENCES
Darlington, S. (Dec. 1978). Filters with chebyshev stop-
bands, flat passbands, and impulse responses of fi-
nite duration. In IEEE Trans. Circuits and Systems.
Vol.CAS-25, No.12, pp.966–975.
Hegde, R. and Shenoi, B. A. (Nov. 1998). Magnitude ap-
proximation of digital filters with specified degrees of
flatness and constant group delay characteristics. In
IEEE Trans. Circuits and Systems II. Vol.45, No.11,
pp.1476–1486.
Laakso, T. I., Valimaki, V., Karjalainen, M., and Laine,
U. K. (Jan. 1996). Splitting the unit delay: Tools for
fractional delay filter design. In IEEE Signal Process-
ing Mag. Vol.13, No.1, pp.30–60.
Lang, M. (Sep. 1998). Allpass filter design and applica-
tions. In IEEE Trans. Signal Processing. Vol.46, No.9,
pp.2505-2514.
Mitra, S. K. and Kaiser, J. F. (1993). Handbook for Digital
Signal Processing. Wiley, New York.
Regalia, P. A., Mitra, S. K., and Vaidyanathan, P. P. (Jan.
1988). The digital allpass filter: A versatile signal pro-
cessing building block. In Proc. IEEE. Vol.76, No.1,
pp.19–37.
Selesnick, I. W. (Jan. 1999). Lowpass filters realizable as
allpass sums: design via a new flat delay filter. In
IEEE Trans. Circuits and Systems II. Vol.46, No.1,
pp.40–50.
Selesnick, I. W. and Burrus, C. S. (June 1998). Generalized
digital butterworth filter design. In IEEE Trans. Signal
Processing. Vol.46, No.6, pp.1688–1694.
Selesnick, I. W. and Burrus, C. S. (Sep. 1996). Exchange
algorithms for the design of linear phase fir filters and
differentiators having flat monotonic passbands and
equiripple stopbands. In IEEE Trans. Circuits and
Systems II. Vol.43, No.9, pp.671–675.
Shenoi, B. A. (1999). Magnitude and Delay Approxima-
tion of 1-D and 2-D Digital Filters. Springer-Verlag,
Berlin, Germany.
Thiran, J. P. (Nov. 1971). Recursive digital filters with max-
imally flat group delay. In IEEE Trans. Circuit Theory.
Vol.CT-18, No.6, pp.659–664.
Tseng, C. C. (Sep. 2003). Design of iir digital allpass filters
using least pth phase error criterion. In IEEE Trans.
Circuits and Systems II. Vol.50, No.9, pp.653–656.
Vaidyanathan, P. P. (Sep. 1985). Optimal design of linear
phase fir digital filters with very flat passbands and
equiripple stopbands. In IEEE Trans. Circuits and
Systems. VVol.CAS-32, No.9, pp.904–917.
Zhang, X. and Iwakura, H. (Feb. 1999). Design of iir digital
allpass filters based on eigenvalue problem. In IEEE
Trans. Signal Processing. Vol.47, No.2, pp.554-559.
Zhang, X. and Iwakura, H. (June 1996). Design of iir digital
filters based on eigenvalue problem. In IEEE Trans.
Signal Processing. Vol.44, No.6, pp.1325–1333.
SIGMAP 2010 - International Conference on Signal Processing and Multimedia Applications
210