BILATERAL TELEOPERATION FOR FORCE SENSORLESS 1-DOF
ROBOTS
Stefan Lichiardopol, Nathan van de Wouw and Henk Nijmeijer
Dept. of Mechanical Engineering, Eindhoven University of Technology, PO Box 513, 5600 MB Eindhoven, The Netherlands
Keywords:
Bilateral teleoperation, Force sensor-less robotic setups.
Abstract:
It is well known that for bilateral teleoperation, force feedback information is needed. In this paper, we propose
a control approach for bilateral teleoperation with uncertainties in the model of the slave robot and which does
not use force sensors for haptic feedback. The controller design is based on a cyclic switching algorithm. In
the first phase of the cyclic algorithm, we estimate the environmental force and in the second phase a tracking
controller ensures that the position of the slave robot is tracking the position of the master robot. A stability
analysis of the overall closed-loop system is presented and the approach is illustrated by means of an example.
1 INTRODUCTION
In this paper, we consider the problem of bilateral
teleoperation in force-sensor-less robotic setups. It is
well-known that haptic robotic devices and teleopera-
tion systems exploit information regarding the exter-
nal forces (see (Lawrence, 1993) and (Hokayem and
Spong, 2006), e.g. for haptic feedback). The slave
robot interacts with the environment and its dynamics
are dependent on external forces induced by this inter-
action. These forces can be contact forces (interaction
forces between environmental objects and the robot)
or exogenous forces induced by the environment.
In bilateral teleoperation, knowledge on the un-
known environmentalforce applied on the slave robot
is typically needed to achieve coordinated teleoper-
ation. One option for obtaining such disturbance
information is to equip the slave robot with force-
sensors; for examples of such robotic devices, es-
pecially haptic devices, which use force sensors the
reader is referred to (Lawrence, 1993), (Yokokohji
and Yoshikawa, 1994). However, in many cases, the
most important external forces for multi-link robots
appear at the end-effector. Note that force sensing
at the end effector of the robot is often not feasible
since the external forces will typically interact with
the load, which the slave robot is e.g. positioning,
directly (and not with the robot end-effector). Be-
sides, in some cases, the position at which the external
forces are applied is a priori unknown and may be on
a robot link as opposed to on the end-effector. More-
over, the usage of force-sensors can be expensive and
increase the production costs of the robot which can
be undesirable especially in domestic applications.
For these reasons, a disturbance estimation
scheme for force-sensor-less robots can be intersting.
Disturbance observers (DOB) have been widely used
in different motion control applications ((White et al.,
1998), (Fujiyama et al., 2000), (Iwasaki et al., 1999))
for determining the disturbance forces, such as fric-
tion forces. However, the performance enhancement
of these DOB strategies may lead to smaller stabil-
ity margins for the motion control ((Komada et al.,
2000)); therefore a robust design with respect to the
environmental disturbances and model uncertainties
is needed. Previous results on robustly stable DOB
((Kempf and Kobayashi, 1999), (Eom et al., 2000),
(G¨uvenc and G¨uvenc, 2001), (Ryoo et al., 2004)) are
based on linear robust control techniques. Some non-
linear DOB have been developed for the estimation
of harmonic disturbance signals ((Chen et al., 2000),
(Liu and Peng, 2000)).
Various strategies have also been considered for
force-sensor-less control schemes estimating the ex-
ternal force. (Eom et al., 1998) proposes an adap-
tive disturbance observer scheme, and (Ohishi et al.,
1991) and (Ohishi et al., 1992) propose an H
∞
esti-
mation algorithm. In (Alcocer et al., 2003), a control
strategy called ”force observer” is introduced. This
design uses an observer-type algorithm for the esti-
mation of the exogenous force. The drawback of this
approach is that it assumes perfect knowledge of the
model of the system.
In parallel with force estimation strategies, based
39
Lichiardopol S., van de Wouw N. and Nijmeijer H. (2010).
BILATERAL TELEOPERATION FOR FORCE SENSORLESS 1-DOF ROBOTS.
In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 39-46
DOI: 10.5220/0002934400390046
Copyright
c
 SciTePress

on disturbance observers, another approach using sen-
sor fusion has been developed to diminish the noise
levels of the force sensors. In (Kr¨oger et al., 2007),
force and acceleration sensors are used, while in (Gar-
cia et al., 2008), data from force sensors and posi-
tion encoders are fused. Sensor fusion provides better
qualitative results than obtained by employing more
expensive force sensors.
Here, we present a control approach for bilateral
teleoperation with an estimation strategy for exter-
nal forces acting on the slave robot with a load with
unknown mass. This method extends a result pre-
sented in (Lichiardopol et al., 2008), which consid-
ered human-robotic co-manipulation problem. The
proposed algorithm is robust for large uncertainties in
the mass of the load.
The paper is structured as follows. Section 2
presents the problem formulation and in Section 3 we
describe the control strategy we propose. In Section
4, we apply the algorithm to a 1-DOF master-slave
robotic setup. In the final section of the paper, the
conclusions and some perspectives on future work are
discussed.
2 PROBLEM STATEMENT
The problem that is tackled in this paper is that of
bilateral teleoperation in force sensor-less robotic se-
tups. We assume that the slave robot is generally car-
rying a load (e.g. tool or product) and that the ex-
ogenous forces act on the slave or on the load. For
1-DOF robotic setups, this assumption does not in-
duce any loss of generality. We consider the case in
which no force sensor is present to measure the ex-
ogenous force directly. Moreover, we consider the re-
alistic case in which the mass of the load is not known
exactly which further challenges the estimation of the
exogenous force. In order to solve this problem, we
propose the design of a force estimator which is ro-
bust to the uncertainties in the mass of the load. In
order to achieve the teleoperation, the position of the
slave robot must track the position of the master robot.
For the sake of simplicity, we have considered iden-
tical master and slave robots. The extension towards
different inertias for the master and slave robots is rel-
atively straightforward by introducing some scaling
factors for the forces applied on the master and slave
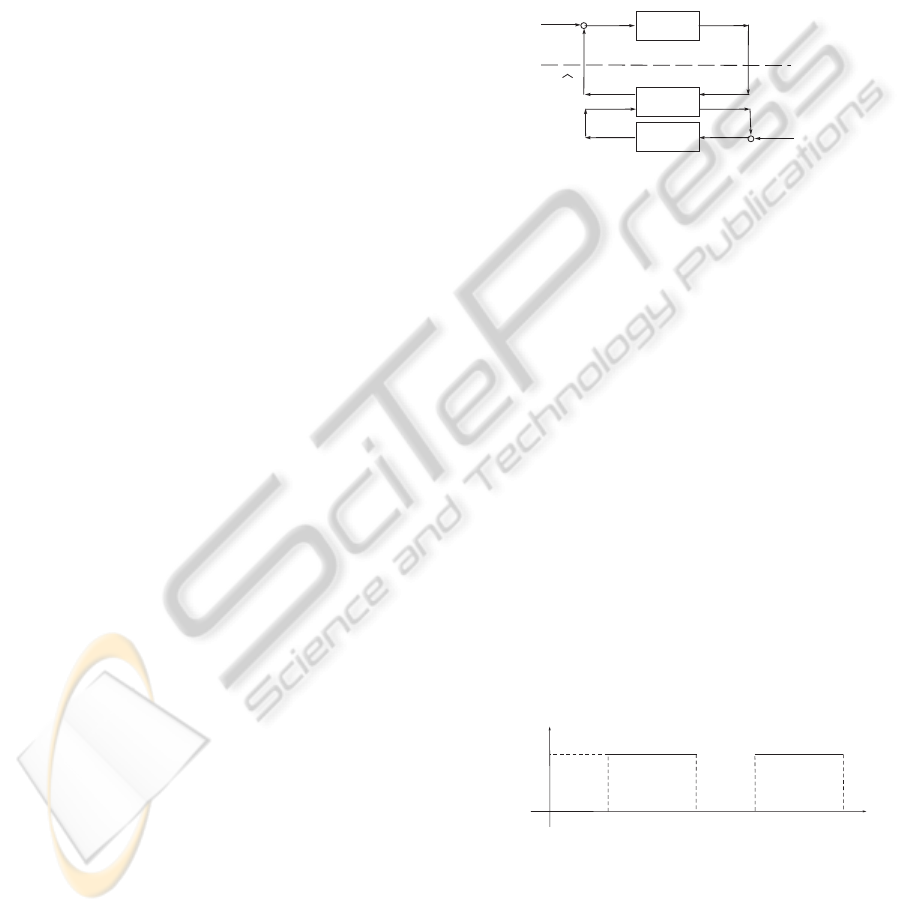
robots. In Figure 1, the block diagram of the teleop-
eration setup is presented with the blocks Master and
Slave representing the dynamics of the master and the
slave robot respectively and the block C representing
the control algorithm for bilateral teleoperation. The
signals F
H
and F
E
represent the human and the envi-
ronmental force respectively; x
M
and x
S
are the posi-
tions of the master and the slave robots, u is the con-
trol signal for the slave robot and
ˆ
F
E
is the signal that
makes transparent the environmental force acting on
the slave robot F
E
to the master cockpit. We adopt the
assumption that the only measurements available are
the position of the joint(s) and hence we aim to con-
struct an output-feedback control strategy.
The objective of this paper is to design the controller
+
+
C
+
+
Master
Slave
F
E
F
H
x
M
x
S
u
F
E
Figure 1: Problem Setup.
C such that the following goals are met:
• the position of the slave robot is tracking the po-
sition of the master robot;
• an accurate estimate of the environmental force is
transmitted to the master robot;
• the overall system is stable.
3 CONTROL DESIGN
Due to the uncertainties in the model of the slave
robot we can not estimate the unknownenvironmental
force and track the master robot position at the same
time (unknowninertia and only position measurement
available do not allow simultaneous force estimation
and position tracking). Therefore, we are proposing a
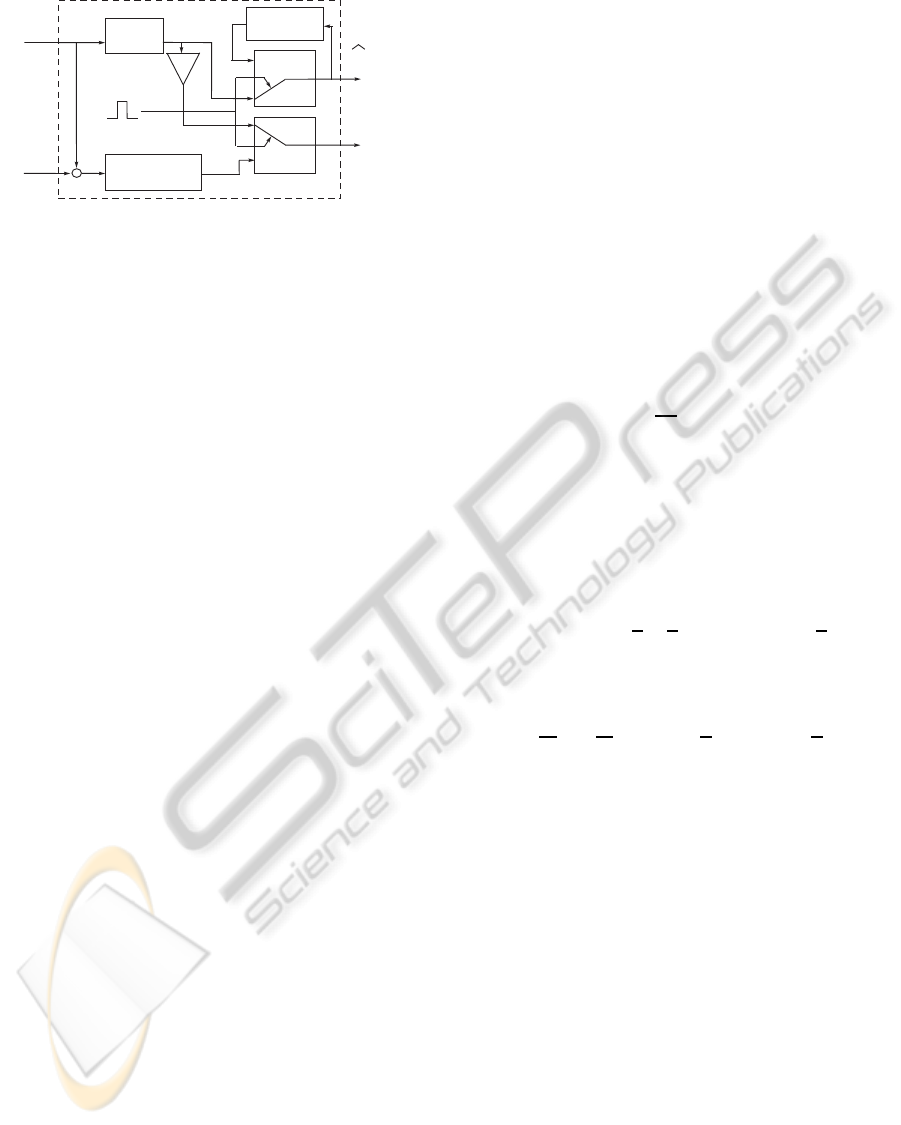
switching controller based on a cyclic algorithm. Dur-
ing one cycle of duration T, we will have two phases
as in Figure 2:
time
Phases of
the algorithm
T
T
0
estimation
phase
tracking
phase
estimation
phase
tracking
phase
2T
T+T
0
0
Figure 2: Temporal division of the control strategy.
1. Estimation of the environmental force;
2. Position tracking.
During the first phase, which last for a period of T
0
(T
0
< T), the controller will behave as a force estima-
tor. Here we are using the force observer introduced
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
40

K
0
K
1
+K
2
s
+
x
S
C
-
s
x
M
F
E
u
Memory
-1
phase I
phase I
phase II
phase II
Figure 3: Controller Design.
in (Lichiardopol et al., 2008) to estimate the exter-
nal force which will be used for the purpose of haptic
feedback and during the second phase we are keep-
ing the estimated force constant. In the second phase,
we are using a PD controller for the slave robot to
track the position of the master robot. In Figure 3, we
present the block diagram representation of the con-
troller where the controller blocks are represented by
their transfer functions in the Laplace domain (s ∈ C)
and the block called Memory saves the last estimate
of the environmental force at the end of the first phase
and provides the same constant output during the en-
tire second phase. The switches in Figure 3 are set on
positions corresponding to the first phase of the algo-
rithm.
In the following section, we study the stability for
the closed-loop system (including force estimation er-
ror dynamics and tracking error dynamics).
3.1 Description
For the purpose of stability analysis, we first formu-
late the model of the error dynamics. In order to ob-
tain the error dynamics, the dynamics of the master
and slaves robots are needed in both phases. During
the first phase (kT ≤ t < kT + T
0
, k ∈ N), the model
dynamics are:

m¨x
M
= F
H
(t)+ K
0
˙x
S
m¨x
S
= F
E
(t)−K
0
˙x
S
, (1)
where x
M
and x
S
are the position of the master and
the slave robots respectively, F
H
and F
E
are the human
and the environmental force, respectively, m is the un-
known inertia of the robot with the load (the mass is
assumed to be bounded m ∈[M
min
,M
max
]) and param-
eter K
0
is a scalar that defines the force estimation al-
gorithm and is chosen such that the estimation of the
force has converged in the interval [kT,kT + T
0
].
In the second phase of the algorithm (kT + T
0
≤
t < (k+ 1)T, k ∈N), the system behavior is described
by:

m¨x
M
= F
H
(t)+
ˆ
F
E
(KT + T
0
)
m¨x
S
= F
E
(t) + K
1
(x
M
−x
S
) + K
2
( ˙x
M
− ˙x
S
)
, (2)
where K
1
and K
2
define the PD controller that ensures
the tracking of the master robot position by the slave
robot (these parameters are chosen such that the poly-
nomial ms
2
+K
2
s+ K
1
is Hurwitz ∀m ∈[M
min
,M
max
])
and
ˆ
F
E
(KT +T
0
) is the estimation of the environmen-
tal force at the end of the first phase.
In the sequel, we assume that the exogenous
forces acting on the system (human force F
H
and envi-
ronmental force F
E
) and their derivativesare bounded.
3.2 Stability Analysis
Let us define the vector ε = [e
x
, ˙e
x
]
T
= [x
M
(t) −
x
S
(t), ˙x
M
(t)− ˙x
S
(t)]
T
, which contains the position and
the velocity tracking errors, and the force estimation
error e
F
=
ˆ
F
E
−F
E
. Then the force error dynamics are
described by:
˙e
F
= −
K
0
m
e
F
−
˙
F
E
, (3)
during the first step of the algorithm (kT ≤t < kT +
T
0
, k ∈N) and
˙e
F
= −
˙
F
E
, (4)
during the second phase (kT + T
0
≤t < (k + 1)T, k ∈
N).
The position error dynamics is represented by:
˙
ε =

0 1
0 0

ε +

0 0
1
m
1
m

F
H
F
E

+

0
2
m

e
F
,
(5)
for t ∈ [kT,kT + T
0
), with k ∈N and
˙
ε =

0 1
−
K
1
m
−
K
2
m

ε +

0
1
m

F
H
+

0
1
m

e
F
,
(6)
for t ∈ [kT + T
0
,(k + 1)T), with k ∈N.
The goal of this section is to prove that the overall
system presented in Figure 1 is input-to-state stable
with respect to the inputs F
H
and F
E
. For this we are
going to use a result introduced in (Jiang et al., 1996)
that states that the series connection of two input-
to-state stable systems is also an input-to-state stable
system. In the sequel, this proof will be split into two
parts:
• Prove that the force error dynamics are stable with
respect to the input
˙
F
E
;
• Prove that the position error dynamics are stable
with respect to the inputs F
H
, F
E
and e
F
.
3.2.1 Input-to-state Stability of the Force
Estimation Error Dynamics
The stability analysis of the force error dynamics is
done by studying the discrete-time input-to-state sta-
bility (ISS) property of the system (3)-(4). For this we
BILATERAL TELEOPERATION FOR FORCE SENSORLESS 1-DOF ROBOTS
41

will now exploit an exact discretisation of the system
at the sampling instances kT.
The solution of system (3) at time t = kT + T
0
,
with k ∈N, is:
e
F
(kT + T
0
) = e
−
K
0
m
T
0
e
F
(kT)+
+
R
T
0
0
e
−
K
0
m
(T
0
− τ )
˙
F
E
(kT + τ )d τ .
(7)
The solution of system (4) at time t = (k + 1)T, with
k ∈ N, is:
e
F
((k+ 1)T) = e
F
(kT + T
0
)
−
R
T−T
0
0
˙
F
E
(kT + T
0
+ τ )d τ .
(8)
Define the sampled force estimation error dynamics
e
k
:= e
F
(kT), with k ∈ N. Combining relations (7)
and (8), one can obtain the discrete-time force esti-
mation error dynamics:
e
k+1
= e
−
K
0
m
T
0
e
k
+ w
k
, (9)
with w
k
=
R
T
0
0
e
−
K
0
m
(T
0
− τ )
˙
F
E
(kT + τ )d τ −
R
T−T
0
0
˙
F
E
(kT + T
0
+ τ )d τ . The system (9) is
input-to-state stable with respect to the input w
k
because



e
−
K
0
m
T
0



< 1, since the parameters K
0
, T
0
and the inertia m are positive. Note that w
k
is bounded
for any bounded
˙
F
E
(t) and bounded T
0
.
Now we exploit a result in (Neˇsi´c et al., 1999) that
says that if the discrete-time dynamics is ISS and the
intersample behavior is uniformly globally bounded
over T,then the corresponding sampled-data is ISS.
The fact that the intersample behavior is uniformly
globally bounded over T directly follows from (3),(4)
with
˙
F
E
bounded, since
e(t) =









e
−
K
0
m
(t−kT)
e
F
(kT)
+
R
t
kT
e
−
K
0
m
(t− τ )
˙
F
E
( τ )d τ
,kT ≤t < kT + T
0
e
F
(kT + T
0
)
−
R
t
kT+T
0
˙
F
E
( τ )d τ
,kT + T
0
≤t < (k + 1)T
.
(10)
3.2.2 Input-to-state Stability of the Tracking
Error Dynamics
Similarly to the study of the force estimation error dy-
namics, we evaluate the input-to-state stability prop-
erty of the tracking error dynamics with respect to the
inputs F
H
, F
E
and e
F
.
The solution of system (5) at time t = kT + T
0
,
with k ∈N, is:
ε (kT + T
0
) = e
A
1
T
0
ε (kT) +
R
T
0
0
e
A
1
(T
0
− τ )
B
11
u(kT + τ )d τ
+
R
T
0
0
e
A
1
(T
0
− τ )
B
12
e
F
(kT + τ )d τ ,
(11)
where A
1
=

0 1
0 0

, B
11
=

0 0
1
m
1
m

, B
12
=

0
2
m

and u(t) =

F
H
(t)
F
E
(t)

.
The solution of system (6) at time t = (k + 1)T,
with k ∈N, is:
ε ((k+ 1)T) = e
A
2
(T−T
0
)
ε (kT + T
0
)
+
R
T−T
0
0
e
A
2
(T−T
0
− τ )
B
21
F
H
(kT + T
0
+ τ )d τ
+
R
T−T
0
0
e
A
2
(T−T
0
− τ )
B
22
e
F
(kT + T
0
+ τ )d τ ,
(12)
where A
2
=

0 1
−
K
1
m
−
K
2
m

, B
21
=

0
1
m

and B
22
=

0
1
m

.
Let us define
ω
k
:= e
A
2
(T−T
0
)
(
R
T
0
0
e
A
1
(T
0
− τ )
B
11
u(kT + τ )d τ
+
R
T
0
0
e
A
1
(T
0
− τ )
B
12
e
F
(kT + τ )d τ )
+
R
T−T
0
0
e
A
2
(T−T
0
− τ )
B
21
F
H
(kT + T
0
+ τ )d τ
+
R
T−T
0
0
e
A
2
(T−T
0
− τ )
B
22
e
F
(kT + T
0
+ τ )d τ
(13)
and ε
k
= ε (kT), with k ∈N. Combining relations (11)
and (12), we obtain the discrete-time system:
ε
k+1
:= e
A
2
(T−T
0
)
e
A
1
T
0
ε
k
+ ω
k
, (14)
where ω
k
is bounded for all k, since T, T
0
are
bounded, F
E
, F
H
are bounded by assumption and e
F
is bounded due to the fact that the force estimation er-
ror dynamics is ISS with respect to
˙
F
E
.
Next, we study the input-to-state stability prop-
erty of the system (14) with respect to the input ω
k
.
But before we carry on this step, we need to evalu-
ate the matrix Q = e
A
2
(T−T
0
)
e
A
1
T
0
. Namely, input-to-
state stability of (14) implies, firstly, the global uni-
form asymptotic stability of ε = 0 when the input ω
k
is zero and the boundness of the error ε for bounded
input.
For the evaluation of the matrix Q, two exponen-
tial matrices must be determined; as the matrix A
1
T
0
depends only on known parameters, we can easily de-
termine its exponential:
E
1
:= e
A
1
T
0
=

1 T
0
0 1

. (15)
In order to compute the exponential of matrix P =
A
2
(T −T
0
), we are using a procedure similar to the
one introduced in (Gielen et al., 2008), which em-
ploys the Cayley-Hamilton theorem, which says that
if p( λ ) = det( λ I
n
−A), with I
n
the n × n identity
matrix, is the characteristic polynomial of a matrix
A ∈ R
n×n
then p(A) = 0. This means that given the
matrix P, for any i ≥ 2, there exists a set of coeffi-
cients a
i
,b
i
∈ R such that the i
th
power of P can be
expressed in terms of its first two powers:
P
i
= a
i
I
2
+ b
i
P. (16)
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
42

Let us now exploit (16) to determine the exponential
of the matrix P:
e
P
=
∞
∑
i=0
P
i
i!
=
∞
∑
i=0
1
i!
(a
i
I
2
+ b
i
P), (17)
or
e
P
=
∞
∑
i=0
a
i
i!
!
I
2
+
∞
∑
i=0
b
i
i!
!
P. (18)
Using the expression of A
2
, we can decompose P as
follows: P = U +
1
m
L, where
U =

0 T −T
0
0 0

(19)
and
L =

0 0
−K
1
(T −T
0
) −K
2
(T −T
0
)

. (20)
Consequently, the expression for the exponential ma-
trix becomes:
e
P
=
∞
∑
i=0
a
i
i!
!
I
2
+
∞
∑
i=0
b
i
i!
!
U +
1
m
∞
∑
i=0
b
i
i!
!
L.
(21)
Let us now define the following scalars:
α = min
m∈[M
min
,M
max
]
∞
∑
i=0
a
i
i!
!
, (22)
α = max
m∈[M
min
,M
max
]
∞
∑
i=0
a
i
i!
!
, (23)
β = min
m∈[M
min
,M
max
]
∞
∑
i=0
b
i
i!
!
, (24)
and
β = max
m∈[M
min
,M
max
]
∞
∑
i=0
b
i
i!
!
. (25)
Given the fact that m ∈ [M
min
,M
max
], we can define
the scalars γ =
1
M
max
and γ =
1
M
min
.
Then there always exist ζ
1
, ζ
2
, ζ
3
∈[0,1] such that:
∞
∑
i=0
a
i
i!
!
= ζ
1
α + (1− ζ
1
) α , (26)
∞
∑
i=0
b
i
i!
!
= ζ
2
β + (1− ζ
2
) β (27)
and
1
m
= ζ
3
γ + (1− ζ
3
) γ . (28)
Introducing relations (26), (27) and (28) into expres-
sion (21) leads to:
e
P
= ( ζ
1
α + (1− ζ
1
) α )I
2
+

ζ
2
β + (1− ζ
2
) β

U
+

ζ
3
γ + (1− ζ
3
) γ

ζ
2
β + (1− ζ
2
) β

L,
(29)
for some ζ
1
, ζ
2
, ζ
3
∈ [0, 1].
Let us define the matrices Γ
1
= 3 α E
1
, Γ
2
= 3 α E
1
,
Γ
3
= 3 β UE
1
, Γ
4
= 3 β UE
1
, Γ
5
= 3 βγ LE
1
, Γ
6
=
3 βγ LE
1
, Γ
7
= 3 βγ LE
1
and Γ
8
= 3 βγ LE
1
, and the
scalars ρ
1
=
ζ
1
3
, ρ
2
=
1− ζ
1
3
, ρ
3
=
ζ
2
3
, ρ
4
=
1− ζ
2
3
, ρ
5
=
ζ
2
ζ
3
3
, ρ
6
=
ζ
2
(1− ζ
3
)
3
, ρ
7
=
(1− ζ
2
) ζ
3
3
, ρ
8
=
(1− ζ
2
)(1− ζ
3
)
3
.
This means that the expression of matrix Q is equiva-
lent to:
Q =
8
∑
i=1
ρ
i
Γ
i
, (30)
with
∑
8
i=1
ρ
i
= 1.
Thus we have now found the generators for a
convex set that overapproximates the matrix Q, with
the uncertain parameter m. Notice that
∑
∞
i=0
a
i
i!
and
∑
∞
i=0
b
i
i!
are infinite sums and will in practice be ap-
proximated by finite sums of length N. Next, we pro-
vide an explicit upper bound on the 2-norm of the ap-
proximation error induced by such truncation.
Theorem 1. Consider an integer N ∈ N and a real
positive scalar ϑ such that
• µ =
q
λ
max
ϑ
< 1, where
λ
max
= max
m∈[M
min
,M
max
]

eig(P
T
P)

, (31)
• ∀i ≥N,
√
ϑ
i
< i!.
Then:





∞
∑
i=N
P
i
i!





2
≤
µ
N
1− µ
. (32)
Proof.



∑
∞
i=N
P
i
i!



2
≤
∑
∞
i=N



P
i
i!



2
≤
∑
∞
i=N
k
P
i
k
2
i!
≤
∑
∞
i=N
√
( λ
max
)
i
i!
,
(33)
where the inequality


A
i


2
2
≤ kAk
2
2
×... × kAk
2
2
=
max(eig((A
T
A))
i
has been used. Using the property
that ∀a ∈ R
+
, ∃N ∈ N such that ∀i ≥ N,
√
a
i
< i!,
inequality (33) becomes:





∞
∑
i=N
P
i
i!





2
≤
∞
∑
i=N
q
( λ
max
)
i
i!
≤
∞
∑
i=N
µ
i
. (34)
Let us now employ the known result of convergence
of geometric series which states that ∀a ∈ [0,1),
lim
n→∞
∑
n
i=0
a
i
= lim
n→∞
1−a
n+1
1−a
=
1
1−a
.





∞
∑
i=N
P
i
i!





2
≤
µ
N
1− µ
. (35)
Using Theorem 1, we can choose N such that the
approximation error is small (even as low as the ma-
chine accuracy).
BILATERAL TELEOPERATION FOR FORCE SENSORLESS 1-DOF ROBOTS
43

In the next theorem , we provide a LMI-based sta-
bility conditions for the discrete-time tracking error
dynamics to be ISS with respect to the input ω
k
.
Theorem 2. Consider the discrete-time system (14).
If there exists a matrix Ω = Ω
T
> 0 and scalar ς ∈
(0,1), such that the following linear matrix inequali-
ties are satisfied:
Γ
i
T
ΩΓ
i
−Ω ≤− ς Ω,i ∈{1,. .. ,8} (36)
where Γ
i
are defined above, then the system (14) is
ISS with respect to the input ω
k
.
Proof. Using the Schur complement, relations (36)
can be written as:

−Ω Γ
i
T
Ω
ΩΓ
i
−Ω

≤ − ς Ω,i ∈{1,...,8}. (37)
Multiplying every inequality (37) with ρ
i
and sum-
ming them up, we obtain:

−Ω
∑
8
i=1
ρ
i
∑
8
i=1
ρ
i
Γ
i
T
Ω
Ω
∑
8
i=1
ρ
i
Γ
i
−Ω
∑
8
i=1
ρ
i

≤ − ς Ω
∑
8
i=1
ρ
i
,
(38)
which according to equation (30) is:

−Ω Q
T
Ω
ΩQ −Ω

≤ − ς Ω, (39)
or
Q
T
ΩQ−Ω ≤ − ς Ω. (40)
Let the candidate Lyapunov function be V
k
=
( ε
k
)
T
Ω ε
k
. We compute △V
k
= V
k+1
−V
k
:
△V
k
= ( ε
k
)
T
Q
T
ΩQ ε
k
−( ε
k
)
T
Ω ε
k
+2( ε
k
)
T
Q
T
Ω ω
k
+ ( ω
k
)
T
Ω ω
k
,
(41)
which according to (40) gives:
△V
k
≤ − ς ( ε
k
)
T
Ω ε
k
+ 2( ε
k
)
T
Q
T
Ω ω
k
+ ( ω
k
)
T
Ω ω
k
(42)
After some straightforward computations, we can
show that:
k ε k
2
≥
2
ς
s
λ
max
λ
min
sup
k∈N
( ω
k
) ⇒ △V ≤ −
ς
2
k ε k
2
2
, (43)
where λ
max
and λ
min
are the largest and the smallest
eigenvalues of matrix Ω, respectively.
(43) implies that system (14) is input-to-state sta-
ble with respect to the input ω
k
; see (Jiang and Wang,
2001) for sufficient condition for the ISS of discrete-
time systems.
Remark 1. For the sake of simplicity, Theorem 2 is
based on a common quadratic ISS Lyapunov func-
tionV = ε
T
Ω ε . Alternatively, a parameter-dependent
Lyapunovfunction approach could straight-forwardly
be exploited to formulate less conservative stability
conditions.
The LMIs (36) are defined for the non-truncated Γ
i
,
but in practice we evaluate the vertex matrices using a
truncation after N iterations as provided by Theorem
1. The errors can be as low as the machine accuracy,
just as the errors obtained from the numerical solver
of the LMIs. Moreover, we can gain some robustness
for these evaluation errors if the scalar ς is chosen
greater than ε
ς
> 0.
The last part of the study of the ISS property of
the tracking error dynamics is to analyze the inter-
sample behavior. Using Theorem 2, we can prove that
the error dynamics are ISS on the sampling instance
t = kT, with k ∈ N. Given the choice of the param-
eters K
1
and K
2
such that the system (6) is Hurwitz
for all m ∈[M
min
,M
max
], we can conclude that during
the second phase (t ∈ [kT + T
0
,(k + 1)T)) the track-
ing error dynamics are bounded. In order to prove
the stability of the overall continuous-time system, we
need to show that the position error dynamics are also
bounded for t ∈ (kT,kT + T
0
).
The solution of system (5), for t ∈ (kT,kT + T
0
)
is:
ε (kT + t) =

1 t
0 1

ε (kT)
+
R
t
0

1 t − τ
0 1

B
11
u(kT + τ )d τ
+
R
t
0

1 t − τ
0 1

B
12
e
F
(kT + τ )d τ .
(44)
As the human force and the environmen-
tal force are bounded, we can define F =
max
t∈(kT,kT +T
0
)
(|F
H
(t)|+ |F
E
(t)|). In the previous
section, we have proven that the force estimation er-
ror dynamics are ISS and consequently are bounded;
therefore there exists E
F
= max
t∈(kT,kT +T
0
)
(|e
F
(t)|).
Considering the three terms from relation (44), we
can conclude that the first one is bounded due to the
boundness of the discrete-time error dynamics, the
second term:




Z
t
0

1 t − τ
0 1

B
11
u(kT + τ )d τ




≤




F
m

T
2
0
2
T
0





,
(45)
and the third:




Z
t
0

1 t − τ
0 1

B
12
e
F
(kT + τ )d τ




≤




2E
F
m

T
2
0
2
T
0





.
(46)
Therefore, we can conclude that the position error dy-
namics are also bounded for t ∈ (kT,kT + T
0
). Sim-
ilarly, to the force estimation error dynamics, we can
employ the result from (Neˇsi´c et al., 1999) to prove
that the tracking error dynamics is ISS because the
discrete-time tracking error dynamics is ISS and the
intersample behavior is uniformly globally bounded.
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
44

Since the force estimation error dynamics (e
F
) is
ISS with respect to the input
˙
F
E
and the tracking error
dynamics ( ε ) is ISS with respect to the inputs F
H
, F
E
and e
F
, we use the result introduced by (Jiang et al.,
1996) concerning the series connection of ISS sys-
tems to conclude that the closed-loop system from
Figure 1 with the controller C with the block diagram
representation from Figure 3 is ISS with respect to the
inputs F
H
, F
E
and
˙
F
E
.
Remark 2. By studying the ISS property of the sys-
tem, one can observe that the steady-state force esti-
mation and tracking errors can be influenced by tun-
ing parameters T, T
0
, K
0
, K
1
and K
2
. The algorithm
provides a deeper insight into these relations. If we
consider the converging manifold that bounds the er-
ror signal we can determine these parameters in ac-
cordance with the desired convergence rate.
Remark 3. In case the environmentalforce F
E
is con-
stant, i.e.
˙
F
E
= 0, the force estimation dynamics are
globally exponentially stable and the tracking error
dynamics is ISS with respect to the inputs F
H
and F
E
.
this means that ”perfect” haptic feedback is provided
and that bounded tracking error remain; therefore the
closed loop is stable.
Remark 4. The exact ”tracking” regulation with re-
spect to what the human has in mind is up to the hu-
man (since the human is in charge of the ultimate po-
sitioning).
4 ILLUSTRATIVE EXAMPLE
In this section, we will apply the control design pro-
posed in the previous section to a master-slave tele-
operation setup consisting of two 1-DOF robots. The
inertia of the robots is considered to be in the range
m ∈[0.1, 10]kg.
The ”human” controller has been emulated by a
linear transfer function:
H(s) =
K
d
(T
d
s+ 1)
T
PL
s+ 1
=
500(1+ s)
0.1s+ 1
, (47)
with saturation at ±100N. Here we use real human
parameters, since the human movement is lower than
6Hz. Also to comply with the human sensing range,
which is between 0Hz and 40 −400Hz depending
on the amplitude of the input signal, we have cho-
sen the parameters are the cycle period of the con-
troller T = 0.01s and the duration of the first stage
T
0
= T/2 = 0.005s. The force estimator acting in the
first phase of the algorithm is defined by parameter
K
0
= 10
5
. The tracking PD controller which is active
during the second phase has the parameters K
1
= 200
and K
2
= 1.
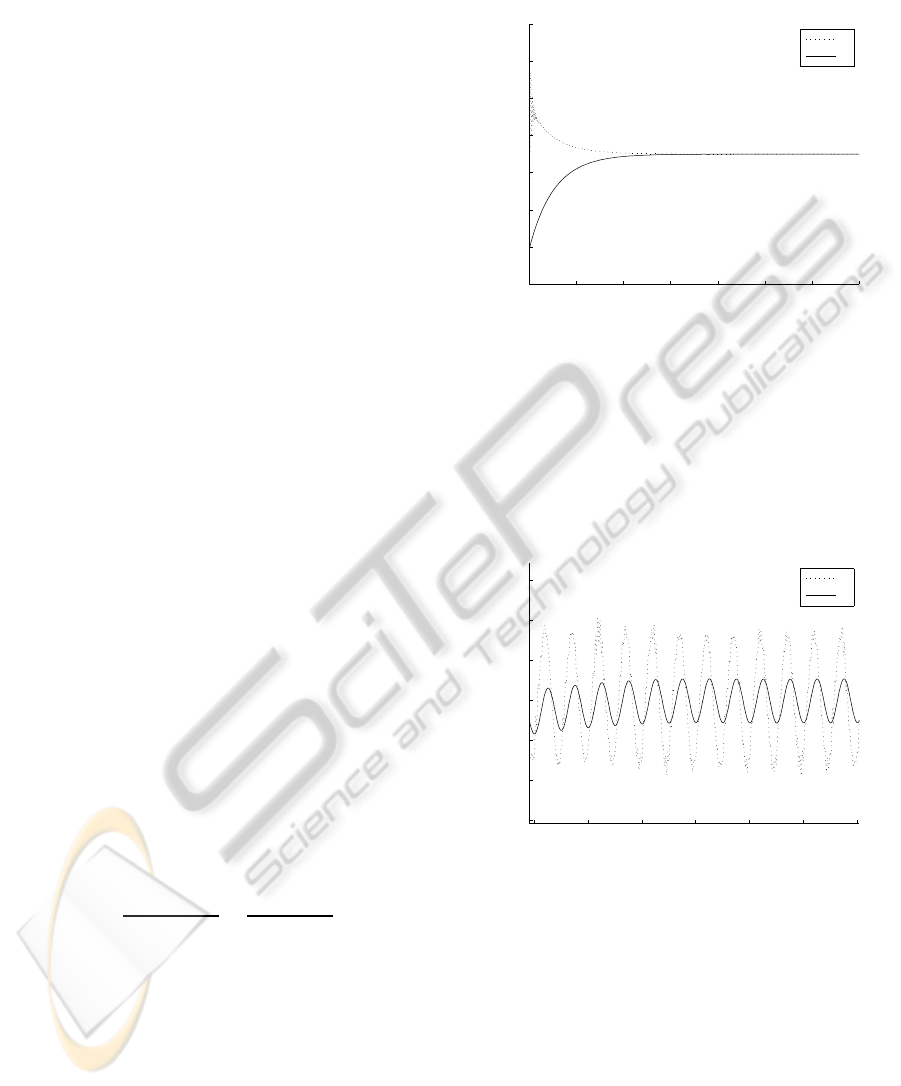
In Figure 4, we simulated the position tracking of the
0 5 10 15 20 25 30 35
−0.1
0
0.1
0.2
0.3
0.4
0.5
0.6
Time [s]
Position [m]
x
M
x
S
Figure 4: Position tracking.
algorithm when the ”human” is performing a move-
ment from 0m to 0.25m on the master robot and a si-
nusoidal external force with amplitude 0.5N and fre-
quency 1Hz is disturbing the slave robot. The dotted
line is the position of the master and the solid line si
the position of the slave.
One can observe that because no disturbance rejec-
22 24 26 28 30 32 34
0.2494
0.2496
0.2498
0.25
0.2502
0.2504
0.2506
Time [s]
Position [m]
x
M
x
S
Figure 5: Position tracking.
tion controller is implemented, the external force is
stopping the position signal to settle at 0.25m. In Fig-
ure 5, a zoomed in version of the Figure 4 that em-
phasizes this aspect is presented.
5 CONCLUSIONS AND
PERSPECTIVES
In this paper, we have introduced a new control al-
gorithm for bilateral teleoperation of 1-DOF robots
in force-sensorless setups using a switching strategy
BILATERAL TELEOPERATION FOR FORCE SENSORLESS 1-DOF ROBOTS
45

between a force estimating controller and a tracking
controller. This switching algorithm guarantees both
the estimation of the environmental force acting upon
the slave robot (to be used in haptic feedback) in the
absence of force sensors and the convergence of the
tracking errors in the case of external perturbations.
We note that the ultimate position setting is the re-
sponsibility of the human, as he is in charge of the
position of the master robot. Finally, we remark that
the proposed algorithm is robust for unknown loads
to be carried by the slave robot.
Future perspectives of this work we will mainly
focus on an extension to multi-degree-of-freedom
robots and also to robots with nonlinear dynamics.
REFERENCES
Alcocer, A., Robertsson, A., Valera, A., and Johansson, R.
(2003). Force estimation and control in robot manip-
ulators. Proceedings of the 7
th
Symposium on Robot
Control (SYROCO’03), pages 31–36.
Chen, X., Komada, S., and Fukuda, T. (2000). Design of a
nonlinear disturbance observer. IEEE Transactions on
Industrial Electronics, 47:429–436.
Eom, K. S., Suh, I. H., and Chung, W. K. (2000). Distur-
bance observer based path tracking of robot manip-
ulator considering torque saturation. Mechatronics,
11:325–343.
Eom, K. S., Suh, I. H., Chung, W. K., and Oh, S. R. (1998).
Disturbance observer based force control of robot ma-
nipulator without force sensor. Proceedings of IEEE
International Conference on Robotics and Automa-
tion, pages 3012–3017.
Fujiyama, K., Katayama, R., Hamaguchi, T., and
Kawakami, K. (2000). Digital controller design for
recordable optical disk player using disturbance ob-
server. Proceedings of the International Workshop on
Advanced Motion Control, pages 141–146.
Garcia, J. G., Robertsson, A., Ortega, J. G., and Johansson,
R. (2008). Sensor fusion for compliant robot motion
control. IEEE Transations on Robotics, 24:430–441.
Gielen, R., Olaru, S., and Lazar, M. (2008). On poly-
topic approximations as a modelling framework for
networked control systems. Proceedings of the Inter-
national Workshop on Assesment and Future Direc-
tion of NMPC, Pavia, Italy.
G¨uvenc, B. A. and G¨uvenc, L. (2001). Robustness of dis-
turbance observers in the presence of structured real
parametric uncertainty. Proceedings of the American
Control Conference, pages 4222–4227.
Hokayem, P. F. and Spong, M. W. (2006). Bilateral tele-
operation: A historical survey. Automatica, 42:2035–
2057.
Iwasaki, M., Shibata, T., and Matsui, N. (1999).
Disturbance-observer-based nonlinear friction com-
pensation in table drive system. IEEE Transactions
on Mechatronics, 4:3–8.
Jiang, Z. P., Mareels, I. M. Y., and Wang, Y. (1996).
A Lyapunov formulation of the nonlinear small-gain
theorem for interconnected ISS systems. Automatica,
32:1211–1215.
Jiang, Z. P. and Wang, Y. (2001). Input-to-state stability for
discrete-time nonlinear systems. Automatica, 37:857–
869.
Kempf, C. J. and Kobayashi, S. (1999). Disturbance ob-
server and feedforward design for high-speed direct-
drive position table. IEEE Transactions on Control
System Technology, 7:513–526.
Komada, S., Machii, N., and Hori, T. (2000). Control
of redundant manipulators considering order of dis-
turbance observer. IEEE Transactions on Industrial
Electronics, 47:413–420.
Kr¨oger, T., Kubus, D., and Wahl, F. M. (2007). Force and
acceleration sensor fusion for compliant manipulation
control in 6 degrees of freedom. Advanced Robotics,
21:1603–1616.
Lawrence, D. (1993). Stability and transparency in bilateral
teleoperation. IEEE Transactions on Robotics and Au-
tomation, 9:624–637.
Lichiardopol, S., van de Wouw, N., and Nijmeijer, H.
(2008). Boosting human force: A robotic enhance-
ment of a human operator’s force. Proceedings of
International Conference on Decision and Control,
pages 4576–4581.
Liu, C. S. and Peng, H. (2000). Disturbance observer based
tracking control. Journal of Dynamic Systems, Mea-
surement and Control, 122:332–335.
Neˇsi´c, D., Teel, A. R., and Sontag, E. D. (1999). Formulas
relating K L -stability estimates of discrete-time and
sampled-data nonlinear systems. Systems & Control
Letters, 38:49–60.
Ohishi, K., Miyazaki, M., Fujita, M., and Ogino, Y. (1991).
H
∞
observer based force control without force sensor.
Proceedings of International Conference on Industrial
Electronics, Control and Instrumentation, pages 1049
– 1054.
Ohishi, K., Miyazaki, M., Fujita, M., and Ogino, Y. (1992).
Force control without force sensor based on mixed
sensitivity H
∞
design method. Proceedings of IEEE
International Conference on Robotics and Automa-
tion, pages 1356 – 1361.
Ryoo, J. R., Doh, T. Y., and Chung, M. J. (2004). Robust
disturbance observer for the track-following control
system of an optical disk drive. Control Engineering
Practice, 12:577–585.
White, M. T., Tomizuka, M., and Smith, C. (1998). Im-
proved track following in magnetic disk drives using
a disturbance observer. IEEE Transactions on Mecha-
tronics, 5:3–11.
Yokokohji, Y. and Yoshikawa, T. (1994). Bilateral control
of master-slave manipulators for ideal kinematics cou-
pling formulation and experiment. IEEE Transactions
on Robotics and Automation, 10:605–620.
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
46