
RISK BASED ACCESS CONTROL WITH UNCERTAIN AND
TIME-DEPENDENT SENSITIVITY
John A. Clark
1
, Juan E. Tapiador
1
, John McDermid
1
, Pau-Chen Cheng
2
, Dakshi Agrawal
2
,
Natalie Ivanic
3
and Dave Slogget
4
1
Department of Computer Science, University of York, York, U.K.
2
IBM Thomas J. Watson Research Center, New York, U.S.A.
3
US Army Research Laboratory, Adelphi, Maryland, U.S.A.
4
LogicaCMG, London, U.K.
Keywords:
Information sharing, Multi-level security, Risk-based access control.
Abstract:
In traditional multi-level security (MLS) models, object labels are fixed assessments of sensitivity. In practice
there will inevitably be some uncertainty about the damage that might be caused if a document falls into the
wrong hands. Furthermore, unless specific management action is taken to regrade the label on an object, it
does not change. This does not reflect the operational reality of many modern systems where there is clearly
a temporal element to the actual sensitivity of information. Tactical information may be highly sensitive right
now but comparatively irrelevant tomorrow whilst strategic secrets may need to be maintained for many years,
decades, or even longer. In this paper we propose to model both security labels and clearances as proba-
bility distributions. We provide practical templates to model both uncertainty and temporally characterized
dependencies, and show how these features can be naturally integrated into a recently proposed access control
framework based on quantified risk.
1 INTRODUCTION
There is a recent concern about the inability of many
organisations, particularly those in the national secu-
rity and intelligence arena, to rapidly process, share
and disseminate large quantities of sensitive informa-
tion. The JASON Report (MITRE, 2004) has rein-
forced the view that the inflexibility of current ac-
cess control models is a major inhibitor when dealing
with dynamic and unpredictable environments. As
an example, in the “Navy Maritime Domain Aware-
ness Concept” paper disseminated by the US Navy
in 2007 (Navy, 2007) it is recognised that non-
traditional operations (e.g. when facing irregular op-
ponents who employ asymmetric methods) generally
require access to information historically unavailable
to decision-makers, as well as sharing intelligence at
all classification levels with other partners. Given
that tasks such as sharing and disseminating informa-
tion play a fundamental role in supporting informed
decision making, such organisations are increasingly
resorting to various ad hoc means to surpass these
“cumbersome” authorisation policies (e.g., granting
“temporary” authorisations for high-sensitive objects;
or, as mentioned in (MITRE, 2004), to follow the line
of the old saying “it is better to ask for forgiveness
rather than for permission”).
An earlier paper (Chen et al., 2007a) has pointed
out one major danger of such practices: they result in
an unaccountable risk of information leakage. Access
control is essentially about balancing risk and benefit,
and a static specification of such tradeoffs is not op-
timal in a dynamic environment. The work in (Chen
et al., 2007a) addresses this issue by making access
control much more flexible. The model, known as
Fuzzy MLS, is based on a quantificationof the risk as-
sociated with every access request. Information flows
are determined by particular policies, which replace
the classical binary “allow/deny” decisions by a more
flexible mechanism based on these risk estimators and
measures of risk tolerance. Interested readers can find
further details on Fuzzy MLS in (Chen et al., 2007a)
and the extended version (Chen et al., 2007b).
In this paper we address two additional questions
related to risk-based access control models: uncer-
tainty and time variation of the security labels. We
motivate our approach below.
5
A. Clark J., E. Tapiador J., McDermid J., Cheng P., Agrawal D., Ivanic N. and Slogget D. (2010).
RISK BASED ACCESS CONTROL WITH UNCERTAIN AND TIME-DEPENDENT SENSITIVITY.
In Proceedings of the International Conference on Security and Cryptography, pages 5-13
DOI: 10.5220/0002935200050013
Copyright
c
SciTePress

1.1 Time and Sensitivity
The traditional model of multi-level security (MLS)
associates security clearances with subjects, security
classifications with objects, and provides a clear de-
cision mechanism as to whether an access request
should be granted or not. Thus for example, the “no
read-up rule” of Bell and La Padula (BLP) model dic-
tates that a read request should be granted only if the
subject clearance dominates the object classification.
The intuition behind this (and behind the correspond-
ing “no-write down” rule) is sound. However, such
rules encode for a pre-determined calculation of risks
and benefits, and in many modern networking situ-
ations will preclude effective operations that can be
justified on a risk basis when the specifics of the con-
text are taken into account. Some situations demand
that higher risks be taken for the sake of operational
benefit. In a recent policy statement, US Director of
National Intelligence Mike McConnell on 15 Septem-
ber 2008 said that the principal goal for risk manage-
ment of any intelligence agency such as the CIA or
the NSA should be to protect the agency’s ability to
perform its mission, not just to protect its informa-
tion assets. One practice that certainly impedes the
ability of an organisation to dispatch its responsibili-
ties is inappropriate classification of data. The perils
of underclassification are obvious; overclassification
is a readily explicable outcome. But overclassifica-
tion does not actually solve the problem it intends to;
rather it leads to a variety of ‘workarounds’ and in-
formal practices that simply take risk-based decision
making outside procedural control (MITRE, 2004),
effectively sweeping the issue under the carpet. As-
sessment of risk is an input into the decision making
process, and it should not define the outcome under
all circumstances. Closer examination of modern ap-
plications reveals further assumptions that underpin
traditional MLS based access control. We shall ad-
dress these in turn.
In implementations of traditional MLS models the
default assumption is that the sensitivity of an object
does not change over time. This principle is generally
known as tranquility and was introduced in the BLP
model to formally ensure that certain security prop-
erties hold over time
1
. For many application scenar-
ios this clearly does not hold. In a military scenario
the identified terrorist target of an air-strike is clearly
1
To be precise, the tranquility principle states that nei-
ther a subject clearance nor an object label must change
while they are being referenced. Strong tranquility inter-
prets this as that security levels does not change at all during
normal operation, whilst weak tranquility allows changes
whenever the rules of a given security policy are not vio-
lated (Bishop, 2002).
vastly more sensitive an hour before the strike than it
is one hour after the strike (when the fact it has been
bombed will generally be apparent to all). In contrast,
the name of any pilot involved in the strike may re-
main sensitive for a considerable period of time. Sim-
ilarly, in a commercial environment, treasury deci-
sions on setting interest rates must be released in a
controlled fashion at pre-specified times to avoid un-
fair market advantages. In a highly mobile tactical
situation a soldier’s current location may be highly
sensitive, but his location yesterday will usually be
less sensitive. Similar arguments hold for subject
clearances. Thus, for example, a subject entering en-
emy territory may have his/her clearance temporarily
downgraded until coming back to a safer location.
Modern collaborative operations will generate a
significant amount of classified data and there would
appear to be a need to prevent a general drift to-
wards significant overclassification. More sophisti-
cated practices will need to be adopted to ensure ap-
propriate information usage in current times. Over-
classification will make appropriate information shar-
ing harder in almost any plausible access control
scheme. Innovative risk benefit tradeoff handling ap-
proaches have been proposed to handle the inflexibil-
ity of traditional MLS, such as budget-based schemes
(e.g. as suggested by (MITRE, 2004)). The price a
requester pays for an access will increase with the es-
timate of the consequent risk, which will be inflated if
the sensitivity label is too conservative. Thus, to give
such innovative schemes the best chances of allow-
ing rational risk-based decision making we must en-
sure that the underlying labelling accurately reflects
the current sensitivity.
We clearly need also to take the time-variant na-
ture of sensitivity into account. Traditionally this
would be achieved by trusted subjects downgrading
information at an appropriate time. This is a plausi-
ble approach for small numbers of documents where
manual consideration can be given. However, the
emergence of data-rich MANET environments forces
us to reconsider this approach and ask: can we use-
fully model the time-varying nature of sensitivity in a
principled yet practical way? In this paper we suggest
some means by which this can be achieved.
1.2 Uncertain Security Levels
The traditional MLS model simply assumes that ob-
jects can be classified with an appropriate label re-
flecting the damage that may result from it falling into
the wrong hands. There is general acceptance that
such assignments are best guesses, and typically re-
flect the order of magnitude of the damage that might
SECRYPT 2010 - International Conference on Security and Cryptography
6

result. This is indeed a valuable construct, but in prac-
tice it will be very difficult to foresee all the implica-
tions of informational release. In particular, the value
of a piece of information to an adversary may de-
pend on what other information he has already. But
in general we do not know what the enemy knows;
this alone should cause us to pause and appreciate the
inherent uncertainty in assigned labels. The same is
applicable to the reliability of individuals (subjects).
In many situations it may be impossible to assess with
sufficient precision the degree of trustworthiness of a
subject. Consider for example a scenario where a mil-
itary operation needs the involvement of police offi-
cers and some civilians. People in these two groups
ought to be provided with security clearances in order
for them to have access to data. But the usual pro-
cedures employed for granting clearances in the mil-
itary context (i.e., investigation of the subject’s back-
ground, etc.) might simply not be affordable here.
In summary, the traditional MLS model is too
strict to consider any form of uncertainty, either on
the security labels or on the subjects’ clearances. As
pointed out in (MITRE, 2004), this limitation is par-
ticularly troublesome in multilateral and coalitional
operations, where we are often required to deal with
new partners in an agile, yet controlled, way. In
this paper we suggest that, in principle, both secu-
rity labels and users’ clearances should be modelled
as a probability distribution, and provide practical and
plausible choices for such distributions.
1.3 Overview
In Sections 2 and 3 we provide practical templates to
model time variation and uncertainty in security la-
bels. The proposed scheme is based on the use of
Beta distributions, which provides us with a suitable
means to model, through parameterisation, a broad
range of specifications. In Section 4 we discuss how
these features can be integrated into the Fuzzy MLS
access control scheme. We stress, however, that this
is merely a convenient example and that the approach
could be applied to other risk- or trust-based access
control schemes. In Section 5 we show how the
notions introduced before can be also extended to
contextual information (e.g., location) considered in
access-control decisions. In Section 6 we discuss how
our approach relates to similar works. Finally, Section
7 concludes the paper by summarising our major con-
tributions and pointing out some avenues for future
research.
2 MODELLING UNCERTAINTY
We choose to model uncertainty in sensitivity la-
belling via a continuous stochastic distribution. This
does not mean that sensitivities are communicated
to the end users in continuous form, rather that
our decision-making infrastructure uses such distri-
butions. Sensitivity label assignment requires judge-
ment. Some judgements will be more uncertain than
others and our modelling approach must cater for
such sophistications. We recall that judgements will
be approximate in any case and so approximate but
practical models will suffice.
Without loss of generality, we shall model sen-
sitivity on a continuous interval [0,S], S > 0. We
make no committment to any interpretation, except
that higher values correspond to higher sensitivity and
vice versa. One could easily map traditional sensitiv-
ity labels onto this scale, e.g. 0 for PUBLIC, 1 for
UNCLASSIFIED, 2 for RESTRICTED, 3 for CON-
FIDENTIAL, 4 for SECRET, 5 for TOP SECRET,
etc. We would wish to allow for symmetric and
skewed (both left and right) distributions, and allow
different variances to be modelled. The Beta distribu-
tion provides a suitable model for our purposes. Beta
distributions are defined over the interval [0,1]. For
α,β > 0, the Beta probability density function (pdf)
is defined by
f(x;α,β) =
x
α−1
(1− x)
β−1
B(α,β)
(1)
where B(α,β) is the beta function
B(x,y) =
Z
1
0
t
x−1
(1− t)
y−1
dt (2)
Some useful properties of the Beta distribution along
with relevant shapes are summarised in Figure 1.
We have now defined the basic Beta distributional
family over the interval [0,1]. We extend this to the
interval of interest by specifying an offset γ ≥ 0 and
an interval length λ > 0. Within the interval of length
λ the distribution will generally be non-zero. The dis-
tribution within this interval is a stretched and nor-
malised Beta distribution defined over [0,1]. Outside
this interval the pdf is zero. This allows us to make
statements like “the classification must be at least RE-
STRICTED but definitely is not TOP SECRET”. This
does not, of course, preclude working over the full in-
terval range, since γ can be set to zero and λ can be
equal to the full sensitivity range. The pdf can be now
be defined as follows
g(x;α,β,γ,λ) =
(
f(
x− γ
λ
;α,β) ∀x ∈ [γ,γ+ λ]
0 ∀x /∈ [γ,γ+ λ]
(3)
RISK BASED ACCESS CONTROL WITH UNCERTAIN AND TIME-DEPENDENT SENSITIVITY
7

Basic properties of the Beta distribution
Expected value E(X) =
α
α+β
Variance Var(X) =
αβ
(α+ β)
2
(α+ β+ 1)
Skewness
2(β− α)
p
(α+ β + 1)
(α+ β + 2)
p
(αβ)
Mode M
0
(X) =
α− 1
α+ β− 2
α > 1,β > 1
0 and 1 α < 1,β < 1
0 (α < 1, β ≥ 1) or (α = 1,β > 1)
1 (α ≥ 1, β < 1) or (α > 1,β = 1)
Not unique α = β = 1
Shape
α = 1,β = 1 ⇒ Uniform [0,1] distribution
α < 1,β < 1 ⇒ U-shaped
α > 1,β > 1 ⇒ Unimodal
(α < 1,β ≥ 1) or (α = 1,β > 1) ⇒ Strictly decreasing
α = 1,β ≥ 2 ⇒ Convex
α = 1,β = 2 ⇒ Straight line
α = 1,1 < β < 2 ⇒ Concave
(α = 1,β < 1) or (α > 1,β ≤ 1) ⇒ Strictly increasing
α > 2,β = 1 ⇒ Convex
α = 2,β = 1 ⇒ Straight line
1 < α < 2, β = 1 ⇒ Concave
0
0.002
0.004
0.006
0.008
0.01
0 0.2 0.4 0.6 0.8 1
Beta(1,10)
0
0.002
0.004
0.006
0.008
0.01
0 0.2 0.4 0.6 0.8 1
Beta(10,1)
α = 1, β = 10 α = 10,β = 1
0
0.0005
0.001
0.0015
0.002
0.0025
0.003
0.0035
0 0.2 0.4 0.6 0.8 1
Beta(2,8)
0
0.0005
0.001
0.0015
0.002
0.0025
0.003
0.0035
0 0.2 0.4 0.6 0.8 1
Beta(8,2)
α = 2, β = 8 α = 8,β = 2
0
0.0005
0.001
0.0015
0.002
0.0025
0 0.2 0.4 0.6 0.8 1
Beta(5,5)
0
0.001
0.002
0.003
0.004
0.005
0 0.2 0.4 0.6 0.8 1
Beta(25,25)
α = 5, β = 5 α = 25,β = 25
Figure 1: Properties of the Beta distribution and some illustrative shapes.
Parameters α, β, γ, and λ can be chosen to provide a
suitable pdf. There is some flexibility as to how such
choices are made. In general γ simply shifts measures
such as mean, mode, and median to the right. Param-
eter λ stretches and serves also to change the variance
(multiplication of any random variable by a constant
λ causes the variance to decrease by a factor of λ
2
).
The Beta distribution also allows left and right skew-
ness to be modelled.
2.1 Mapping into Suitable Beta
Distributions
The use of Beta distributions is an implementation
convenience and is not intended for immediate pre-
sentation to the end users. (The average user will not
take too well to being asked for parameters to a Beta
distribution!) However, we can expect the user to an-
swer plausibly question such as:
• What seems the most appropriate classification of
this information (P, U, R, C, S, TS)?
• How confident are you that this classification is
correct? Pretty confident or not so confident?
• Is it more likely to be classified too high than too
low?
• Is there a time after which this information would
cease to be classified as it is? If so, what might be
the next classification?
From such questions we can provide a technical map-
ping to our parametric models.
An alternative to estimate the Beta parameters
consists of relying on the opinions provided by a num-
ber of individuals
2
. If we assume we can collect a
number of samples x
1
,...,x
N
(N ≥ 2) regarding the
sensitivity of an object, we proceed as follows. We
first compute the sample mean ¯x and variance ¯v By
using the method of moments, parameters α and β
can be then estimated as
α = ¯x
¯x(1 − ¯x)
¯v
− 1
(4)
β = (1− ¯x)
¯x(1 − ¯x)
¯v
− 1
(5)
These estimators can be directly used to define the
target distribution. If a more precise estimation is re-
quired, we can proceed iteratively as follows. Once
α and β are obtained, the estimated distribution is
used to generate a sufficiently large number of ran-
dom samples. These are then presented to the end
users, who are asked to remove values considered as
definitely wrong. The resulting, “filtered” dataset is
used again to produce new estimators for α and β,
and the procedure is repeated until convergence is
reached.
2
It is not the purpose of this work to provide criteria re-
garding how to choose such individuals. We simply assume
they are personnel with appropriate qualifications to carry
out such a task.
SECRYPT 2010 - International Conference on Security and Cryptography
8

3 MODELLING TIME
VARIATION
Above we indicated that a constant label will not re-
flect the true sensitivity of many aspects of data in a
dynamic network environment. The true sensivity of
data will exhibit some trajectory. Sensitivity may go
down but, in principle, also up. Furthermore, the par-
ticular type of trajectory followed will vary with con-
text. But if we are to handle time-variant sensitivity,
we must be able to model it in some way that the user
accepts as plausibly reflecting operational reality. In
this section we provide a variety of simple templates
for temporal dependencies of sensitivity whose ratio-
nale can be effectively communicated to end-users.
Several templates come to mind when considering
temporal dependencies:
1. Fixed.
class(o,t) = K ∀t ≥ 0
with K > 0 constant. The classification remains
constant over time.
2. Step Function.
class(o,t) = K
i
∀t ∈ [t
i
,t
i+1
)
with 0 = t
0
< t
1
< · · · < t
n−1
< t
n
= ∞ and K
i
> 0
constants. The classification changes according
to some step function. This includes the case
where a previously classified object becomes pub-
lic knowledge after some specified period of time.
3. Linear Decay.
class(o,t) = max{0,K · t + K
0
}
with K < 0 and K
0
> 0 (again K and K
0
constants).
This is the simplest case of progressive loss of
sensitivity over time.
4. Exponential Decay.
class(o,t) = K · e
−αt
∀t ≥ 0
with K > 0 and α > 0. This is straightforward case
of continuous loss of sensitivity over time.
The above are not intended to be exhaustive. Fur-
ther fundamental templates can be created and com-
bined as desired. For example, sensitivity might be
constant for a while and then decay. Sensitivity may
also increase over time: the step function can model
increasing sensitivity and further fundamental tem-
plates can be created to model it continuously.
We now assume that the sensitivity whose tempo-
ral trajectory we have just modelled represents some
measured and communicable parameter of a distri-
bution. Next we elaborate on how temporal require-
ments can be integrated with uncertainty modelling.
3.1 Putting the Two Together
We have now defined simple but plausible templates
for the temporal evolution of particular sensitivity
descriptors and have indicated how at any particu-
lar point in time uncertainty in the sensitivity can be
modelled using a stretched and offset Beta distribu-
tion. We need to put the two together, and this can be
achieved in several ways.
In the most general case, the temporal evolution
can be specified by a list of time instants and Beta
parameters of the form
[t
i
,(α
i
,β
i
,γ
i
,λ
i
)] (6)
for i = 0,1,.... The semantics are clear: sensitivity in
the interval [t
i
,t
i+1
] is given by a Beta g(x;α
i
,β
i
,γ
i
,λ
i
)
as defined in expression (3). This allows us to capture
in a simple manner any desired variation in time and
uncertainty – see, for example, Figure 2(a).
A more compact form can be provided in some
cases. The sensitivity distribution over time can be
also defined by a Beta of the form
g(x;α(t),β(t),γ(t), λ(t)) (7)
This allows us to simultaneously model changes in
uncertainty and sensitivity. For example, in Figure
2(a) a Beta with parameters α = β = 3 is initally
shifted 5 positions to the right to model a classifica-
tion “between 5 (SECRET) and 6 (TOP SECRET),
with mean 5.5 and a symmetric shape”. The template
given by functions γ(t), α(t) and β(t) allows to:
1. reduce exponentially the sensitivity level of the
object: the more time elapsed, the less significant
the changes; and
2. reduce progressively the amount of uncertainty
and approach a delta function.
Figures 2(b) provide another example where the
skewness of the distribution is taken into account.
This might be useful, for example, to coach require-
ments of the form “sensitivity should evolve conser-
vatively, i.e. not allowing too much uncertainty on
low security levels”.
The above merely constitute some illustrative ex-
amples. The scheme is sufficiently general as to ac-
commodate many other temporal templates.
RISK BASED ACCESS CONTROL WITH UNCERTAIN AND TIME-DEPENDENT SENSITIVITY
9
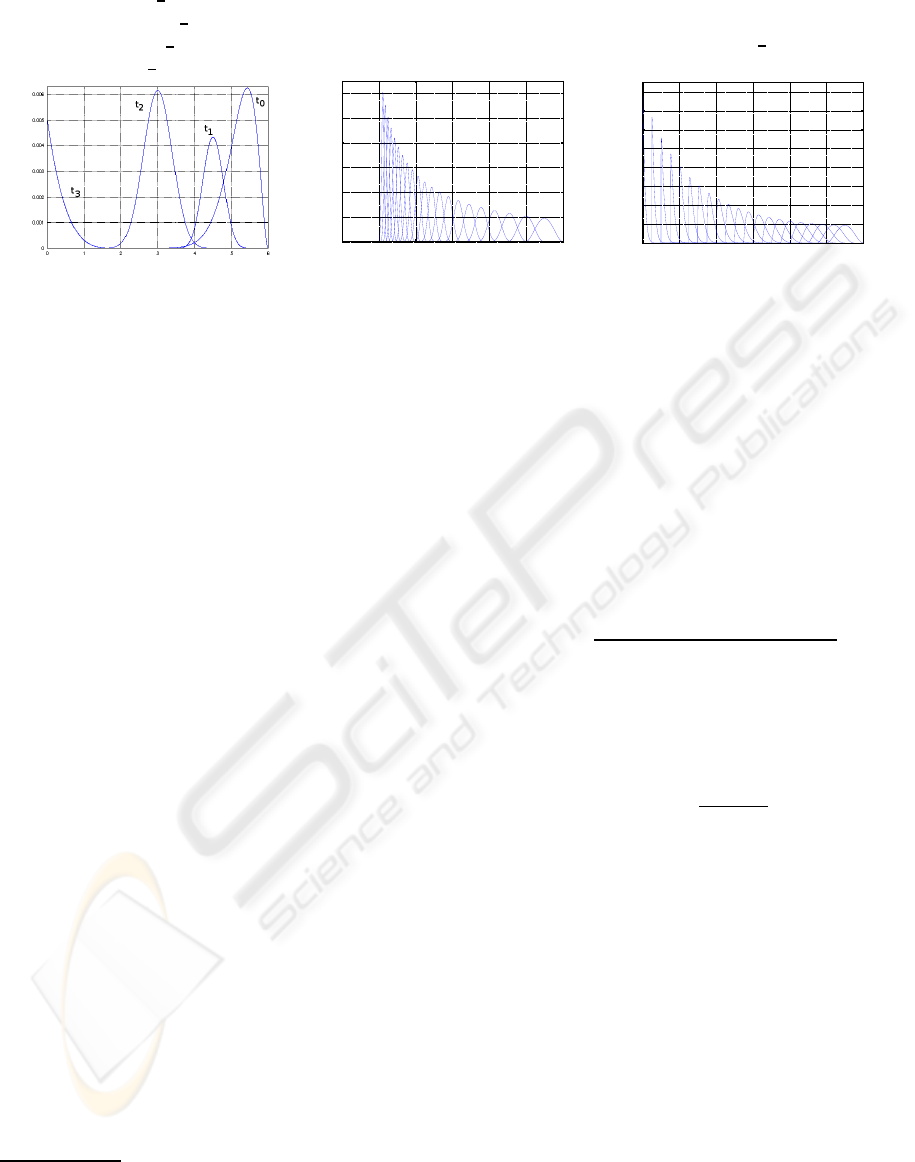
[t
0
,(20,3,0,
1
6
)]
[t
1
,(15,15,−1,
1
3
)]
[t
2
,(30,30,0,
1
6
)]
[t
3
,(1, 2,0,
1
6
)]
(a)
α(t) = 1.2α(t − 1), α(0) = 3
β(t) = 1.2β(t − 1), β(0) = 3
γ(t) = 0.9γ(t − 1), γ(0) = −5
λ(t) = 1
0
0.002
0.004
0.006
0.008
0.01
0.012
0 1 2 3 4 5 6
(b)
α(t) = 0.95α(t −1), α(0) = 3
β(t) = 1.1β(t − 1), β(0) = 3
γ(t) = γ(t − 1) +
1
4
, γ(0) = −5
λ(t) = 1
0
0.002
0.004
0.006
0.008
0.01
0.012
0.014
0.016
0 1 2 3 4 5 6
(c)
Figure 2: Examples of templates for time-varying sensitivity with uncertainty. In figures (b) and (c) distributions evolve
towards the left, i.e., the rightmost distribution corresponds to the label at time t
0
, the next one to t
1
, and so on.
4 INTEGRATING UNCERTAIN
AND TIME-VARYING
SENSITIVITIES WITH
RISK-BASED ACCESS
CONTROL
We now describe how the templates introduced above
can be integrated into an access-control model based
on quantified estimators of risk. Altough not cov-
ered here, a similar approach could be attempted with
trust-based schemes. For the purposes of this pa-
per, we will use the Fuzzy MLS model (Chen et al.,
2007a) as a convenient framework. For complete-
ness and readability, we first provide a brief review of
the model. Subsequently we show how the proposals
above can be integrated within this framework.
4.1 Review of Fuzzy MLS
In (Chen et al., 2007a), risk
3
is defined as a function
of the “gap” between subject’s and object’s security
level (sl and ol, respectively)
risk(sl, ol) = Val(ol) · P(sl,ol) (8)
Here Val(ol) is the estimated value of damage upon
disclosure of the object. The security level is gener-
ally considered to represent the order of magnitude of
damage, and hence Val is defined as
Val(ol) = a
ol
(9)
for some a > 1. Note that it is implictly assumed that
higher sensitivity corresponds to higher values of the
object’s security level ol.
3
This quantifies the risk concerned with the simple se-
curity property (no read-up) of the Bell-La Padula model.
Please see (Chen et al., 2007b) for details about how Fuzzy
MLS addresses the concern of the ∗–property.
The probability of unathorised disclosure,
P(sl, ol), is defined as a combination of two factors
as
P(sl, ol) = P
1
(sl,ol) + P
2
(sl,ol) − P
1
(sl,ol)P
2
(sl,ol)
(10)
The first term, P
1
(sl,ol), measures the probability that
a user with security level sl leaks information of level
ol by succumbing to temptation. It is defined as a
sigmoid of the form
P
1
(sl,ol) =
1
1+ exp(−k(TI(sl,ol) − mid))
(11)
The term TI(sl,ol), called the temptation index,
roughly indicates how much a subject with security
level sl is tempted to leak information with level ol. It
is defined as
TI(sl,ol) =
a
−(sl−ol)
M − ol
(12)
The intuition for the above formulae can be found in
(Chen et al., 2007a). The number mid in expression
(11) is the value of TI that makes P
1
equal to 0.5,
and the term k serves to control the slope of P
1
. The
value of m is the ultimate object sensitivity, and the
TI approaches infinity as ol approaches M. (The idea
here is that access to an object with sensitivity level
M or greater should be granted by a human being and
not a machine.)
The second component, P
2
(sl,ol), is a measure of
the probability of inadvertent disclosure for informa-
tion belonging to a given category, regardless of the
object’s security level. We shall not elaborate on it, as
the extensions proposed in this paper do not affect it
directly. Please refer to (Chen et al., 2007a) for fur-
ther details.
SECRYPT 2010 - International Conference on Security and Cryptography
10

4.2 Integrating with Distributions
Fuzzy MLS assumes that both the subject and object
labels are static. We can readily incorporate uncertain
and time-dependent sensitivities into the risk estimate
as follows. In order to simplify the notation, from now
on we will denote by l
o
(x,t) the pdf associated with
the security level of object o at time t. The variable x
indicates the sensitivity and ranges from 0 to S (e.g.,
in previous examples we used S = 6). The same nota-
tion will be used for subjects clearances. Thus the pdf
of a user s will be denoted by l
s
(x,t)
Given a subject s and and object o to be accessed
at time t, the tempation index is defined as
TI
′
(s,o,t) =
Z
S
0
Z
S
0
TI(x, y)l
o
(x,t)l
s
(y,t)dxdy
=
Z
S
0
Z
S
0
a
−(x−y)
M − y
l
o
(x,t)l
s
(y,t)dxdy
(13)
Expression (16) constitutes the natural extension of
the TI to a continuous case, where the index is com-
puted over the entire range(s) of sensitivities given by
the Beta distributions. Consequently, the probabil-
ity of unauthorised disclosure, nowdenoted P
′
1
(s,o,t),
can be computed as in expression (11), although now
using TI
′
(s,o,t) rather than the previous TI(sl,ol).
Regarding the estimated value of damage, expres-
sion (9) can be replaced by
Val
′
(o,t) =
Z
S
0
a
x
l
o
(x,t)dx (14)
analogously as it was done for the temptation index.
At a given time t, risk can be computed as before,
i.e. weighting the value of damage by the probability
of unauthorised disclosure as
risk
′
(s,o,t) = Val
′
(o,t) · P
′
(s,o,t) (15)
In a practical implementation, previous expres-
sions can be easily replaced by discrete approxima-
tions for convenience.
5 EXTENDING UNCERTAINTY
TO CONTEXTUAL
INFORMATION
It is widely recognised that many access control de-
cisions should depend not only on the identities of
the subject and object involved, but also on the con-
text where the access will take place. Thus for ex-
ample, a user might have unconditional access to a
document provided he is at the office and the request
is done between 9 am and 5 pm. Context informa-
tion is often assumed to be publicly available. How-
ever, when used as an input to an access control de-
cision it should be properly verified or else ensure
(e.g., by cryptographic means) its correctness. Loca-
tion, for example, is usually referred as an important
factor when dealing with access control decisions.
Ensuring that the location provided by the requester
is authentic may not always be an easy affair (see
e.g. (Brands and Chaum, 1993; Denning and Mac-
Doran, 1996; Sastry et al., 2003) for some possible
solutions). In some scenarios, measures to guarantee
the authenticity of the requester’s location may not be
available, and therefore some uncertainty will be in-
evitably present on this information. But uncertainty
comes from other sources as well. In a battlefield we
may want to associate a security label to each location
in a map, in such a way that access to information
depends, among other attributes, on the requester’s
current position. Such labels should not be static as-
sessments of sensitivity, for in a dynamic and unpre-
dictable environmentthe situation around a position is
likely to change over time (e.g. if the enemy moves).
Location only constitutes a particular example of
contextual information generally taken into account
to grant or deny access to information. In the area of
risk-based access control, Cheng and Karger (Chen
and Karger, 2008) have identified multiple contex-
tual factors that may contribute to information leak-
age. These factors consider security-relevant features
of the information systems, communication channels,
physical environment and human users. In practi-
cal terms, specific measures of such factors are inter-
preted as risk indices which, combined together, con-
tribute to assess the global risk.
The templates introduced above to model uncer-
tainty in labels and clearances can be directly applied
to context information, particularly in the form of risk
factors. If c is a contextual variable (e.g., location,
time), a time-varying probability distribution l
c
(x,t)
can be associated to c. The domain of x is now spe-
cific to c (e.g. coordinates in a 2D battlefield, a time
interval). We assume that for each c there exists a
function r
c
(x) mapping each value of x into [0, 1], and
we interpret this as the risk incurred by granting ac-
cess to a request when c = x. Uncertainty in c can now
be taken into account as before, so the contextual risk
introduced by c is given by
r
′
c
(t) =
Z
r
c
(x)
x
l
c
(x,t)dx (16)
Expression (15) should be modified so that con-
textual factors help to modulate the risk purely de-
rived from the MLS model. We propose a multiplica-
RISK BASED ACCESS CONTROL WITH UNCERTAIN AND TIME-DEPENDENT SENSITIVITY
11

tive scheme of the form
risk(s,l, c
1
,...,c
k
,t) = risk
′
(s,o,t) ·
k
∏
i=1
r
′
c
(t) (17)
where c
1
,...,c
k
are contextual variables involved in
the decision making.
6 RELATED WORK
The need for access control schemes more flexible
than classical approaches has been repeatedly pointed
out in recent years, particularly in the context of mo-
bile ad hoc networks. Even though the concept of
“risk” is explicitly mentioned by many authors, the
great majority of the new models actually rely on a
notion of “trust” among parties in order to make ac-
cess decisions. Trust and risk are indeed related and
might be used interchangeably in some contexts, but
in an essential sense they are different concepts.
Dimmock et al (Dimmock, 2003; Dimmock et al.,
2004) explored the relationships between trust, risk
and privileges in a trust-based access control setting.
Their proposal relies on the idea of granting or deny-
ing access depending on the trust it has in the request-
ing principal and the risk of granting the request. In-
tuitively, the higher the risk of access, the higher the
trust needed in the requester to grant access. In (Dim-
mock et al., 2004) the authors propose a quantifiable
definition of risk based on the classical combination
of cost and likelihood of outcomes. This model is
later discarded in (Dimmock et al., 2004) due, accord-
ing to the authors, to the “insufficient expressiveness
of the risk metrics to capture all the subtleties con-
veyed by the trust value”. Instead, the policy author is
provided with a language to express specific rules to
compare trust and expected cost information.
Tuptuk and Lupu discuss in (Tuptuk and Lupu,
2007) a very similar idea, namely to use risk to de-
termine the level of trust needed to access a resource.
For an authorisation to take place, a measure of trust
in the requester needs to exceed a givenrisk threshold.
The risk threshold is acknowledgedto be dynamic and
mainly dependent on the current context. This work,
however, assumes that the metric to obtain such a risk
is given.
Diep et al propose in (Diep et al., 2007) to make
access decisions after a risk assessment of both the re-
quest and the context. Risk is estimated for the classi-
cal three security properties (confidentiality, integrity
and availability), again as a combination of cost and
likelihood in a particular context, and then a global
risk index is computed.
Though related to the our approach, none of these
works explicitly address the notion of risk in an MLS
setting.
7 CONCLUSIONS AND FUTURE
WORK
Risk-based access control models–and particularly
those based on a quantified definition of risk, such
as Fuzzy MLS–may be of help to address some of
the difficulties that classical schemes are experienc-
ing when dealing with dynamic and unpredictable en-
vironments. In this paper we have shown how mod-
els such as Fuzzy-MLS can be extended to effectively
process uncertain and time-varying security specifica-
tions. By explicitly expressing sensitivity as a proba-
bility distribution, both security labels and clearances
are, in a sense, more accurate in their purpose of re-
flecting real-world situations. We have also shown
how these notions can be extended to contextual in-
formation.
In future work we will address questions related
to the language needed to express authorisation poli-
cies based on risk assessment with uncertainty. Fuzzy
logic seems a natural candidate for such a purpose.
In Section 6 we have given account of some re-
cent works exploring the idea of using risk to deter-
mine the level of trust required to access a resource.
The converse seems not to have been so well studied;
namely, can we exploit (quantifiable) trust measures
to determine risk? Consider for instance the scenario
discussed in Section 2.1, where the (distribution asso-
ciated with the) label of an object is obtained from the
opinionsof a number of experts. Such inputs might be
somehow weighted by a measure of trust on the sub-
ject’s organisation, agency, expertise, etc. This and
other relationships between access control, trust and
risk will be explored in future work.
ACKNOWLEDGEMENTS
This research was sponsored by the U.S. Army Re-
search Laboratory and the U.K. Ministry of De-
fence and was accomplished under Agreement Num-
ber W911NF-06-3-0001. The views and conclusions
contained in this document are those of the authors
and should not be interpreted as representing the offi-
cial policies, either expressed or implied, of the U.S.
Army Research Laboratory, the U.S. Government, the
U.K. Ministry of Defence or the U.K. Government.
The U.S. and U.K. Governments are authorized to re-
SECRYPT 2010 - International Conference on Security and Cryptography
12

produce and distribute reprints for Government pur-
poses notwithstanding any copyright notation hereon.
REFERENCES
Bishop, M. (2002). Computer Security: Art and Science.
Addison-Wesley.
Brands, S. and Chaum, D. (1993). Distance-bounding pro-
tocols. In EUROCRYPT’93, pages 344–359. Springer-
Verlag. LNCS 765.
Chen, P.-C. and Karger, P. (2008). Risk modulating fac-
tors in risk-based access control for information in a
manet. Technical report, IBM.
Chen, P.-C., Rohatgi, P., Keser, C., Karger, P., Wagner, G.,
and Reninger, A. (2007a). Fuzzy multi–level secu-
rity: An experiment on quantified risk–adaptive ac-
cess control. In IEEE Symposium on Security and Pri-
vacy, pages 222–230. IEEE Press.
Chen, P.-C., Rohatgi, P., Keser, C., Karger, P., Wagner, G.,
and Reninger, A. (2007b). Fuzzy multi–level secu-
rity: An experiment on quantified risk–adaptive ac-
cess control. Technical report, IBM.
Denning, D. and MacDoran, P. (1996). Location-based au-
thentication: Grounding cyberspace for better secu-
rity. Computer Fraud & Security, 2:12–16.
Diep, N., Hung, L., Zhung, Y., Lee, S., Lee, Y.-K., and Lee,
H. (2007). Enforcing access control using risk assess-
ment. In Proc. 4th European Conference on Universal
Multiservice Networks, pages 419–424.
Dimmock, N. (2003). How much is ‘enough’? risk in trust-
based access control. In IEEE Int. Workshops on En-
abling Technologies: Infrastructur for Collaborative
Entreprises – Enterprise Security, pages 281–282.
Dimmock, N., Belokosztolszki, A., Eyers, D., Bacon, J.,
and Moody, K. (2004). How much is ‘enough’? risk
in trust-based access control. In SACMAT’04, pages
156–162.
MITRE (2004). Horizontal integration: Broader
access models for realizing information domi-
nance. Technical report, The MITRE Corpora-
tion, JASON Program Office, Mclean, Virginia.
http://www.fas.org/irp/agency/dod/jason/classpol.pdf.
Navy (May 2007). Navy maritime domain aware-
ness concept. Technical report, Department of
the Navy. http://www.navy.mil/navydata/cno/Navy
Maritime Domain Awareness Concept FINAL 2007
.pdf.
Sastry, N., Shankar, U., and Wagner, D. (2003). Secure
verification of location claims. In ACM Workshop on
Wireless Security.
Tuptuk, N. and Lupu, E. (2007). Risk based authorisation
for mobile ad hoc networks. In AIMS, pages 188–191.
Springer-Verlag. LNCS 4543.
RISK BASED ACCESS CONTROL WITH UNCERTAIN AND TIME-DEPENDENT SENSITIVITY
13
