TRUST DEGREE BASED ACCESS CONTROL FOR
SOCIAL NETWORKS
Bo Lang
State Key Lab of Software Development Environment
Beijng University of Aeronautics and Astronautics, Beijing, 100191, China
Keywords: Trust Management, Access Control, Trust Degree based Access Control, Trust Graph Calculation.
Abstract: Trust brings a new method for building scalable and fine-grained access control mechanism of social
networks, a new kind of P2P systems. In this paper, the semantics of trust in the context of access control is
described, and a Trust Degree Based Access Control model named TDBAC is proposed. Trust degree
computing on a trust network is a key part in TDBAC. A novel algorithm that transforms a trust network to
a computable expression is given. The algorithm simplifies the computation process and is also flexible.
1 INTRODUCTION
In its early days, P2P was mostly used for file
sharing among anonymous peers, but systems which
provide resource sharing among specific groups of
people gradually become popular. Such systems
include special interest groups, scientific research
document sharing, desktop grid, knowledge sharing,
et al. This kind of systems are called social networks
(Fast, Jensen, and Neil, 2005) or Group-centric
systems (Krishnan, Sandhu, Niu, and Winsborough,
2009) in which nodes are linked by some special
relations. In social networks, privacy of users needs
to be protected. Also in systems such as provider
allies in B2B environment where users are always
competitors, the access to sensitive information
should be restricted. Therefore, fine grain access
control is needed. However, as users always need to
interact with unknown entities, the control of the
interactions between strange users is a new problem
arising.
Traditional access control methods such as DAC,
MAC and RBAC are closed and static, and can not
handle the requests from unknown users.
Enlightened by the trust based interaction
mechanism of human society, people suggested
introducing trust into distributed computing, and
making trust the basis for decision making. In 1996,
Blaze et al in AT&T laboratory firstly coined the
concept of “Trust Management”(TM) (Blaze,
Feigenbaum, and Lacy, 1996)
.
From then on, the
concept of TM is widely used in distributed
applications, such as electronic business systems
(Atrf, 2002). In TM, trust relations are established
by issuing public key certificates; the numerical
range of a trust value is the set {0, 1} which means
distrust and trust. In recent years, the researches on
computational trust models which aim at
representing trust degrees using computable
numbers or structures attract much attention. Basing
on trust degree, fine grain access control security
policy could be supported.
This paper probes into the method of building
scalable and flexible access control mechanism for
social networks. A trust degree based access control
framework is put forward, and an algorithm for trust
calculation is proposed.
Section 2 of the paper analyzes the properties
and the semantics of trust in access control; section
3 proposes the trust degree based access control
model TDBAC; section 4 defines the algorithm for
calculating trust on a trust network; section 5
discusses related work and section 6 gives
conclusions.
2 TRUST AND
ACCESS CONTROL
In social science, the definition and characteristics
of trust have been well studied. A typical definition
43
Lang B. (2010).
TRUST DEGREE BASED ACCESS CONTROL FOR SOCIAL NETWORKS.
In Proceedings of the International Conference on Security and Cryptography, pages 43-48
DOI: 10.5220/0002936300430048
Copyright
c
 SciTePress

of trust was given by Gambetta, and he believed that
trust is a particular level of the subjective probability
with which an agent will perform a particular action
in a context (Gambetta,1988). This definition shows
that: firstly, trust is a subjective opinion, and it is
subjective in nature. This is because the evaluation
of trust depends on the trustor to a great extent;
secondly, trust does not only have binary value, that
is, trust or distrust, there are different levels of trust;
and thirdly, trust is also related to a specific
situation, i.e. the context of the interaction.
People also found that trust should have certain
transitivity when some restrictive conditions are
added. Abdul-Rahman and Josang et al. pointed out
that this kind of restrictive condition mainly refers to
the existence of a recommendation (Abdul-Rahman,
2004)(Jøsang, Hayward, and Pope, 2006). This
paper gives the definition of trust transitivity as
follows:
Definition 1: The Transitivity of Trust.
If
AB
t
A
B
,
BC
t
BC
, and
:
BC
t
BCA
, then
AC
t
A
C
, and (, ), ,
A
CABBCACABACBC
tftttttt,
where
AB
t
A
B
represents that A trusts B and the
trust value is t
AB
and [0,1]
AB
t  ;
:
BC
t
BCA
represents that B recommends C to A and the
recommended trust value of B for C is t
BC
and
[0,1]
BC
t  .
Just because of the conditional transitivity, trust
in human society is scalable and open. When trust is
introduced into access control for social networks,
this characteristic will also make the trust based
access control model scalable and flexible.
Conditional transitivity of trust forms a prerequisite
for establishing trust degree based access control.
The semantics of trust in access control can be
described by its attributes. According to the aim of
access control (ISO,1989)( Lampson,1971), the two
main attributes of trust are the ability of protecting
information confidentiality and the ability of
protecting information integrity. Also these
attributes can be further described by their sub-
attributes. According to the attributes of trust, a
quantificational trust measurement model can be
built, which forms another prerequisite for trust
degree based access control.
In social networks, entities can form trust
networks or trust graphs through various kinds of
relations, such as friendship, administration or
cooperation relations. Two entities in the network
which are not directly linked may be strangers to
one another. However, by the recommendations of
the intermediate entities, these strangers may trust
each other to some extent. This kind of trust is called
indirect trust or recommended trust, and the degree
of the trust can be calculated.
The set of the entities that are directly trusted by
an entity A is called the trust group of A, and is
denoted by
()TrustG A . Let E
i
(i=1,2,…n) represent
entities, t
i
，
j
（ i, j=1,2,…,n ） represent the trust
degree ( i.e. trust value) of E
i
to E
j
. The definition
of trust chain and trust graph is given below.
Definition 2: Trust Chain.
For entity A, B and C, if
( )(( ( )) ( ) : )
BC
t
B B TrustG A C TrustG B B C A  
, then A,B,C form a trust chain, denoted as
TrustChain(A,C).
Definition 3: Trust Graph.
All the trust chains from entity E
i
to entity E
k
construct a directed graph which is composed of a
vertex set E and the arcs between the vertexes, and
is denoted by TrustGraph(E
i
, E
k
). An arc from E
p
to
E
q
is represented by
t
pq
p
q
E
E
.
3 TDBAC
In social networks, an entity owning privileges can
delegate the privileges to the entities that he trusts
under certain conditions, which makes the privilege
propagate through the trust graph and dynamically
enlarge the user group of the resource. Different
from the inference-based access control method of
TM, Trust Degree Based Access Control (TDBAC)
is a trust-calculation-based access control model, as
shown in Figure 1. In TDBAC, the trust value which
represents the trust degree of the requested entity to
the requestor is calculated according to the trust
graph between them, and access decisions are made
based on the trust value.
TDBAC is mainly composed of three functions:
quantificational trust expressing, trust degree
calculating and policy evaluation. The latter two
functions collectively constitute the access control
decision making module. The quantificational trust
expressing function represents direct trusts in
TrustGraph(A,B). The trust-graph based trust degree
calculation function takes TrustGraph(A,B) as input,
calculates the trust value of A to B, i.e. t
A,B
.
The trust degree based security policy can be
described by a binary tuple:
TDBAC_Policy (t
threshold
, operation), where
SECRYPT 2010 - International Conference on Security and Cryptography
44

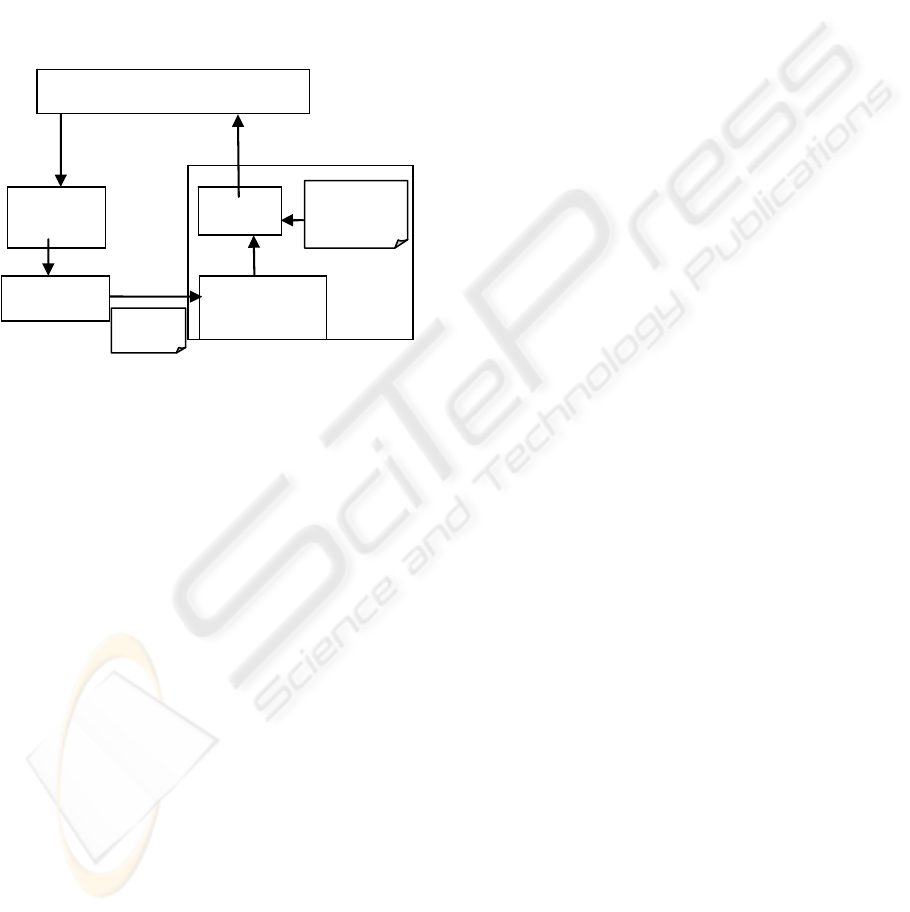
t
threshold
is the low threshold of trust degree.
The meaning of the binary tuple is that, if the
trust value of the requestor satisfies
threshold
tt , then
the request of the designated operation will be
permitted, otherwise the request will be denied.
Policy evaluation function takes request(B,A,o),
the trust value of the requestor t
AB
, and the security
policy TDBAC_Policy
i
(t
0
, o) as inputs. If t
AB
satisfies
0AB
tt , then the access control decision
will be grant(B,A,o), otherwise the result will be
deny(B,A,o).

Policy
evaluation
ADF
TrustGraph
(A,B)
Trust‐graphbased
trustdegree
calculatin
g

request(B,A,o)
Trustdegree
basedsecurity
policies
grant(B,A,o)/
deny(B,A,o)
t
A,B

request(B,A,o)
ADF‐AccesscontrolDecisionmakingFunction
Aisarequestedentity
Bisarequestor
oisanoperation
Quantificational
trustexpressing
Trustrelatio n
finding
AccesscontrolEnforcementFunction
Figure 1: The structure of TDBAC.
By integrating trust concepts with the traditional
access control theory, TDBAC defines a general
structure for implementing trust degree based fine-
grained access control, which is necessary but not
systematically defined at present.
The core of TDBAC is the access-control-
oriented computational trust model, which defines
quantificational trust expression and the algorithm
of calculating trust on a trust graph. Basing on the
quantificational trust expression method proposed in
another paper(Lang, Wang,
and Wang, 2007), this
paper further discusses trust calculation on a trust
graph.
4 TRUST DEGREE CALCULATION
ON A TRUST GRAPH
In TDBAC, the trust between the requested entity
and the requestor is the recommended trust and is
described by the trust graph between them. As
defined in definition 3, a trust graph is constructed
by iteratively connecting and combining direct trusts
between nodes, and the process of trust value
calculating is considerably complex.
Calculus of recommended trust takes a trust
graph as input. There are two basic operators in the
calculus, one is connection for computing
concatenated trust relations, and the other is
combination for combining trust from several
recommendations. For a trust graph, if we regard the
arcs as the operands and the connection and
combination operations as operators, then a trust
graph can be expressed as an expression. If we
further give mathematic definitions to the operands
and operators, then the trust value calculation can be
transformed into normal expression calculation. The
expression that represents a trust graph can be called
a Formal Trust graph Expression (FTE), and the
expression transformed from a FTE which can be
calculated can be called a Computable Trust graph
Expression(CTE). Basing on this analysis, a FTE
based trust degree calculation method is suggested.
4.1 Formal Expression of a Trust
Graph
Before giving the definition of FTE, some related
items are defined:
Definition 4: Trust arc.
Let E be the set of nodes in TrustGraph(E
i
, E
k
),
,
A
EB E

 , then [A → B,t
AB
] defines an arc from
A to B which means that A trusts B and the trust
value is t
AB
. [A → B,t
AB
] can also be denoted as
TrustArc(A,B,t
AB
). A trust arc can be regarded as a
special case of trust chain.
Definition 5: The Connection and Combination of
Arcs.
Let “·” and “+” be the connection and combination
operators respectively. For arcs [A
→ B,t
AB
] ， [B →
C,t
BC
]:
[A
→ B,t
AB
] ·[B → C,t
BC
] means that arc [A →
B,t
AB
] and [B → C,t
BC
] are connected by node B,
which forms a trust chain TrustChain(A,C), and
TrustChain(A,C) = [A
→ B, t
AB
]·[B → C, t
BC
]=[ A → B
→ C, t
AB ,
t
BC
] ;
[A
→ C, t
AC
]+[B → C, t
BC
] means that arc [A → C
， t
AC
]and [B → C,t
BC
] are combined at node C.
Definition 6: The Formal Trust Graph Expression
(FTE).
A Trust graph TrustGraph(E
i
, E
k
) can be described
by a trust graph expression which is constructed
TRUST DEGREE BASED ACCESS CONTROL FOR SOCIAL NETWORKS
45

with trust arcs and operators including “·” ， “+” ，
“
（ ） ”, and is denoted as exp(TrustGraph(E
i
, E
k
)):
exp(TrustGraph(E
i
, E
k
)) = （ TrustArc(E
m
,E
n
),(),· ， +
）） , ,
mn
E
EE .
The priority of the operators is:
（ ）， · ， +.
For the example shown in Figure 2, the
expression of trust graph from E
1
to E
6
is:
exp(TrustGraph(E
1
,E
6
))
=[ E
1
→ E
2
,t
1,2
]· [E
2
→ E
3
,t
2,3
] · （ [E
3
→ E
4
,t
3,4
]
(1)
[E
4
→ E
6
,t
4,6
]+ [E
3
→ E
5
,t
3,5
] · [E
5
→ E
6
, t
5,6
] ）

E
1

E
2

E
3
E
4

E
5

E
6
t
1,2

t
2,3

t
3,4

t
3,5

t
4,6

t
5,6

Figure 2: An example of trust graph.
4.2 The Virtual Arc Iteration
Algorithm
How to generating FTE of the trust graph is the key
in the FTE based trust calculation. In this section, a
virtual arc iteration algorithm which constructs the
FTE exp(TrustGraph(E
1
, E
m
)) from the trust graph
TrustGraph(E
1
, E
m
) is proposed .
Definition 7: Virtual Arc.
The nodes in the trust graph which are the end
points of more than one directed arcs are called
convergent nodes. Let E
j
be a convergent node and
E
1
be a node other than E
j
, then define
TrustArc(E
1
,E
j
) as a virtual arc from E
1
to E
j
, which
is denoted as
VTrustArc(E
1
,E
j
) = [E
1

E
j
, t
i,j
] = exp(TrustGraph(E
1
,
E
j
)).
VTrustArc(E
1
,E
j
) corresponds to the trust graph
between E
1
and E
j
, and the trust value t
1,j
is the
recommended trust from E
1
to E
j
, hence
VTrustArc(E
1
,E
j
) is called a virtual arc. Latter
convergent nodes, for example E
k
, which uses E
j
as
the intermediate recommending node will use
VTrustArc(E
1
, E
j
) to construct the FTE
exp(TrustGraph(E
1
, E
k
)). The request node E
m
may
be the last convergent node in TrustGraph(E
1
, E
m
),
and exp (TrustGraph(E
1
, E
m
)) will have all the
iterative virtual arcs in the trust graph. Replacing the
virtual arcs with their FTEs will clear up all the
virtual arcs and get the final trust graph expression,
i.e. exp(TrustGraph(E
1
, E
m
)). The description of the
virtual arc iteration algorithm is as follows:
(1) For the trust graph TrustGraph(E
1
, E
m
) that
contains m nodes, finding all the k trust chains
by using the forward search or the backward
search algorithms:
TrustChain
i
(E
1
, E
m
),i=1,…,k
(2) Scanning TrustChain
i
(E
1
, E
m
),i=1,…,k, all from
the starting entity E
1
to the target entity E
m
, and
repeating the following operations until the last
convergent node E
m
is met:
 Determining the convergent nodes
Finding E
j
which has more than two different
proceeding nodes in TrustChain
i
(E
1
,
E
m
),i=1,…,k, and E
j
is determined as a
convergent node.
 Defining the virtual arcs
Replacing TrustChain(E
1
, E
j
) in TrustChain
i
(E
1
,
E
m
),i=1,…,k with the virtual arc VTrustArc(E
1
,
E
j
) and remove the repeated chains.
(3) For the final n (n<=k) chains TrustChain
i
(E
1
,
E
j
),i=1,…,n, which do not contain any
convergent node, get the exp(TrustGraph(E
1
,
E
m
)).
(4) For each convergent node E
j
, j∈[2,m],
substituting virtual arc VTrustArc(E
1
, E
j
) in
exp(TrustGraph(E
1
, E
m
)) with
exp(TrustGraph(E
1
, E
j
)), hereby clearing up all
the virtual arcs and getting the final FTE
exp(TrustGraph(E
1
, E
m
)).
The virtual arc iteration algorithm first represents
the trust graph TrustGraph(E
i
, E
k
) using a set of
trust chains, and then finds the convergent nodes
and replaces the chains in TrustGraph(E
i
, E
c
) (E
c
is a convergent node) with VTrustArc(E
i
, E
c
) all by
scanning and manipulating these chains. Also, the
chains are scanned from the starting node E
i
, which
makes each scanning and replacing operation run on
simplified trust chains, and avoids any nested
iterative operations. Hence, virtual arc iteration
algorithm greatly decreases the complexity of trust
value computing.
The example shown in Figure 3 further explains
the virtual arc iteration algorithm. Figure 3 (a) is a
trust graph from A to G which contains 7 nodes.
There are 7 trust chains between A and G, as shown
in Figure 3(b), the trust value of each trust arc is
omitted in the trust chain expressions.
By scanning the trust chains in figure 3(b), the
first convergent node D is found. TrustGraph(A,D)
is composed of the two marked trust chains [A→D]
SECRYPT 2010 - International Conference on Security and Cryptography
46

and [A→B→D]. Then a virtual trust arc
VTrustArc(A,D) = [A

D] can be constructed and
used to substitute the trust chains between A and D.
The result is shown in figure 3(c).

TrustChain1:[A→D→G]
TrustChain2:[A→B→D
→G]
TrustChain3:[A→B→C→G] 
TrustChain4:[A→B→C→E
→F→G]
TrustChain5:[A→B→C→F→G]
TrustChain6:[A→E→F→G] 
TrustChain7:[A→F→G]
A
B
C
D
E
F
G
t
AB

t
BD

t
FE

t
FG

t
BC

t
AE

t
AD

t
DG

t
CG

t
CE

t
AF

t
CF

(a) (b)
(c) (d)

TrustChain1:[A

D→G]
TrustChain2:[A→B→C→G]
TrustChain3:[A

F→G]
B
C
D
F
G
t
AB

t
BC

t
AE

t
AD

t
DG
t
CG
t
CF

A
(e) (f)
Figure 3: An example of the virtual arc iteration algorithm.
Scanning the trust chains in Figure 3(c), the
second convergent node E will be found. The virtual
trust arc VTrustArc(A,E) = [A

E] is composed of
the two marked trust chains. The simplified trust
chains are as shown in Figure 3(d). Continues
scanning , the third convergent node F can be found.
The virtual trust arc VTrustArc(A,F) = [A

F] is
composed of the three marked trust chains. The
simplified trust chains are shown in Figure 3(e).
The trust chains in Figure 3(e) do not contain
any convergent nodes except for G. The trust graph
corresponding to these trust chains is shown in
Figure 3 (f). We can get the expression of
TrustGraph(A,G) as:
exp(TrustGraph(A, G))
= [A

D→G]+[ A→B→C→G]+[ A

F→G]
(2)
= [A

D] ·[D→G] +[A→B] ·[B→C] ·[C→G]
+[ A

F] ·[F→G]
The expressions of the virtual arc [A

F],
[A

E] and [A

D] are as follows:
[A

F] = exp(TrustGraph(A,F))
= [A→B] ·[B→C] ·[C→F]
(3)
+ [A

E] ·[E→F]+ [A→F]
[A

E]= exp(TrustGraph(A,E))
(4)
=[A→B] ·[B→C] ·[C→E]+[A→E]
[A

D]= exp(TrustGraph(A,D))
(5)
=[A→D]+[A→B] ·[B→D]
Basing on equation (3),(4) and (5), the virtual
arcs in equation (2) can be cleared up, and the
expression of TrustGraph(A, G) should be written as:
exp(TrustGraph(A, G))
= ([A→D]+[A→B] ·[B→D]) ·[D→G] +[A→B]
·[B→C] ·[C→G]+([A→B] ·[B→C] ·[C→F]
+( [A→B] ·[B→C] ·[C→E]+[A→E] ) ·[E→F]
+ [A→F] ) ·[F→G]
4.3 Transforming a FTE into a CTE
A FTE exp(TrustGraph(E
1
, E
m
)) needs to be
transformed into a CTE which takes trust values as
operands and the connection and combination
operations as operators. Basing on the definition of
FTE, the transformation rule can be easily defined:
abstracting the trust value t from every arc and
replacing each arc with its trust value. For example,
arc [A
→ B,t
A,B
] should be replaced by t
A,B
, and for the
FTE defined in equation (1), we can get following
CTE after transformation:
1,6 1,2 2,3 3,4 4,6 3,5 5,6
()ttttttt 
(6)
In a CTE, the representation format of trust value
t
i,j
and the calculators of the connection and
combination operation
· and + are not fixed. Hence,
CTE is a generic form and can be customized for
working with different computational trust models,
which shows that this computing method is flexible
and applicable. For example, in the quantificational
trust expression model described in (Lang, et
al.,2007) , t
A,B
is defined by a trust vector V
A,B
;
“·”and “+” are defined by the connection and
combination operators
 and  . Then the CTE
between E
1
and E
6
presented in equation (6) should
be:
V
1, 6
=V
1,2
 V
2,3
 (V
3,4
 V
4,6
 V
3,5
 V
5,6
)
(7)
Calculating equation (7), we can get the trust
vector of E
1
to E
6
.
5 RELATED WORK
In calculation methods proposed by Richardson,
Agudo et al, all paths in the trust network between
the two entities are firstly enumerated, then the trust
Trust Chain 1: [A

D→G]
Trust Chain 2: [A→B→C→G]
Trust Chain 3: [A

E→F→G]
Trust Chain 4: [A→B→C→F→G]
Trust Chain 5: [A→F→G]
Trust Chain 1: [A

D→G]
Trust Chain 2:[A→B→C→G]
Trust Chain 3:[A→B→C→E
→F→G]
Trust Chain 4:[A→B→C→F→G]
Trust Chain 5:[A→E
→F→G]
Trust Chain 6:[A→F→G]
TRUST DEGREE BASED ACCESS CONTROL FOR SOCIAL NETWORKS
47

degree associated with each path is calculated by
applying a concatenation function to the trusts along
the path, and finally those trust degrees are
combined with an aggregation function (Richardson,
Agrawal, and Domingos, 2003) (Agudo, Fernandez-
Gago, and Lopez, 2008). In this method, a trust
graph is regarded as several independent paths,
which is not so reasonable since the effect of trust
combinations at the intermediate entities is omitted.
Huang et al proposed an algorithm to make trust
aggregation in a trust network, which recursively
simplifies a more complex network to a simpler one,
by replacing multiple parallel paths into a single arc.
Each replacement is made by using connection or
combination operation (Huang and Nicol, 2009).
Huang’s algorithm and the algorithm proposed in
this paper all take the connection and the
combination operations in accordance with the
process of trust formation. However, this paper
proposes a novel idea that is to transform a graph
into an expression. The algorithm first transforms a
trust graph into a computable expression, and then
computes the expression to get a trust degree value.
The expression is not specific to any trust expression
structures and trust operators, which makes the
model more flexible.
6 CONCLUSIONS
In this paper, the meaning of trust in the context of
access control is analyzed, and a framework for
implementing trust degree based access control
(TDBAC) in social networks and an algorithm for
trust degree computing on a trust graph is proposed.
The framework shows how trust can be used to
realize fine-grained access control.
For the problem of trust degree calculation based
on a trust graph, the concepts of the formal trust
graph expression (FTE) and the computable trust
graph expression (CTE) are proposed. A virtual arc
iteration algorithm is defined for generating a FTE
from a trust graph. The FTE does not bind to any
specific trust expression structure and the
connection or combination operators. Hence, the
FTE based trust calculation method not only
simplifies trust computations on a complicated
directed graph, but also makes the calculation more
flexible and applicable.
ACKNOWLEDGEMENTS
The Work was supported by the National Science
Foundation of China under Grant No. 60573037, the
Hi-Tech Research and Development Program of
China under Grant No. 2007AA010301, and the
National Basic Research Program of China under
Grant No. 2005CB321901.
REFERENCES
Abdul-Rahman, A., 2004. A Framework for Decentralised
Trust Reasoning, PhD thesis, University of London
Agudo, I., Fernandez-Gago, C., and Lopez, J., 2008. A
Model for Trust Metrics Analysis, TrustBus, LNCS
5185, pages 28–37.
Atrf, Y., 2002. Building Trust in E-Commerce, IEEE
Internet Computing.
Blaze, M., Feigenbaum, J., Lacy, J., 1996. Decentralized
trust management, IEEE Conference on Security and
Privacy, Oakland, CA.
Fast, A., Jensen, D., and Neil Levine B., 2005. Creating
social networks to improve peer-to-peer networking.
Proceedings of the eleventh ACM SIGKDD
international conference on Knowledge discovery in
data mining, pages 568–573, NY, USA.
Gambetta, D., 1988. editor. Trust: making and breaking
cooperative relations. Basil Blackwell.
Huang, J., and Nicol, D., 2009. A Calculus of Trust and
Its Applications to PKI and Identity Management,
Proceedings of the 8th Symposium on Identity and
Trust on the Internet.
ISO, 1989. ISO 7498-2, OSI security architecture.
Jøsang, A., Hayward, R., Pope, S., 2006. Trust Network
Analysis with Subjective Logic. Proceedings of the
Australasian Computer Science Conference
(ACSC'06), Hobart.
Krishnan, R., Sandhu, R., Niu, J., Winsborough, W. H.，
2009. Formal Models for Group-Centric Secure
Information Sharing, Technical Report CS-TR-2009-
002. Department of Computer Science ， The
University of Texas, San Antonio.
Lampson, B. W.，1971. Protection， Proceedings of 5th
Princeton Conf. on Information Sciences and Systems,
Princeton, pages 437-443.
Lang, B., Wang, Z., Wang, Q., 2007. Trust Representation
and Reasoning for Access Control in Large Scale
Distributed Systems, Proceedings of the Second
International Conference on Pervasive Computing
and Applications, Birbingham, England.
Richardson, M., Agrawal, R., Domingos, P., 2003. Trust
Management for the Semantic Web. Proceedings of
the International Semantic Web Conference, pages
351-368.
SECRYPT 2010 - International Conference on Security and Cryptography
48