
EXTENDED VISUAL CRYPTOGRAPHY SCHEME FOR COLOR
IMAGES WITH NO PIXEL EXPANSION
Xiaoyu Wu, Duncan S. Wong and Qing Li
Department of Computer Science, City University of Hong Kong, Tat Chee Avenue, Hong Kong, China
Keywords:
Information hiding, Extended visual Cryptography, Secret sharing.
Abstract:
A k-out-of-n Extended Visual Cryptography Scheme (EVCS) is a secret sharing scheme which hides a secret
image into n shares, which are also some images. The secret image can be recovered if at least k of the shares
are superimposed, while nothing can be obtained if less than k shares are known. Previous EVCS schemes
are either for black-and-white images or having pixel expansion. In this paper, we propose the first k-out-of-n
EVCS for color images with no pixel expansion. The scheme also improves the contrast of the n shares and the
reconstructed secret image (i.e. the superimposed image of any k or more shares) by allowing users to specify
the level of each primary color (i.e. Red, Green and Blue) in the image shares as well as the reconstructed
secret image.
1 INTRODUCTION
In (Naor and Shamir, 1994), Naor and Shamir in-
troduced the notion of Visual Cryptography Scheme
(VCS) which allows an image to be encrypted so that
the decryption can be done simply by the human vi-
sual system without any other computation. A k-out-
of-n VCS splits an image to n shares so that they look
indistinguishable from random noise. These shares
are then printed on transparencies as images. From
any less than k shares, nothing (other than the size) of
the secret image can be obtained. Only by superim-
posing k or more shares, the secret image will become
visible.
In (Naor and Shamir, 1994), an extension of
VCS called Extended Visual Cryptography Scheme
(EVCS) was also introduced. In an EVCS, besides
generating n shares for a secret image, these n shares
also carry n meaningful and independently chosen
images. To generate these shares, a user arbitrarily
chooses n meaningful images which have the same
size as the secret image. Then the user splits the se-
cret image and embed the share information into the n
meaningful images in such a way that given any k− 1
or less shares, no information about the secret image
can be obtained, while given any k or more shares,
the secret image will be revealed when the shares are
superimposed. In (Ateniese et al., 1996), Ateniese et
al. proposed the first k-out-of-n EVCS for black-and-
white images using the hypergraph coloring method.
It is for black-and-white images. Since then, there
have been some other EVCS schemes proposed, e.g.
(Nakajima and Yamaguchi, 2002; Wang et al., 2009;
Sirhindi et al., 2009). To the best of our knowl-
edge, there is no EVCS for color images that supports
the general k-out-of-n secret sharing while having no
pixel expansion, that is, the pixel expansion rate being
equal to one.
In this paper, we solve this problem by propos-
ing the first k-out-of-n EVCS for color images with-
out pixel expansion. We use a probabilistic technique
(Yang, 2004) for achieving no pixel expansion. The
scheme also allows a user to choose the number of
color levels for each primary color (i.e. Red, Green
and Blue) that the reconstructed image and each share
image could have. The reconstructed image refers to
the image obtained by imposing k or more share im-
ages. We find that this ‘tunable’ feature is very useful
(in practice), as the user is able to use it for maximiz-
ing the quality of the reconstructed image, given that
different types of images may best appear with differ-
ent color levels (more details will be given in the later
part of the paper).
2 A BRIEF REVIEW OF K-OUT-
OF-N BLACK-AND-WHITE VCS
In this section, we briefly review a generic represen-
tation of the k-out-of-n VCS scheme for black-and-
423
Wu X., S. Wong D. and Li Q. (2010).
EXTENDED VISUAL CRYPTOGRAPHY SCHEME FOR COLOR IMAGES WITH NO PIXEL EXPANSION.
In Proceedings of the International Conference on Security and Cryptography, pages 423-426
DOI: 10.5220/0002936904230426
Copyright
c
SciTePress
white images(Naor and Shamir, 1994). A k-out-of-
n VCS scheme for black-and-white images is repre-
sented by two collections of n × l boolean matrices.
The two collections are denoted by C
0
and C
1
. Matri-
ces in C
0
(resp. C
1
) are obtained by permuting all the
columns of a Basic Matrix B
0
(resp. B
1
). Formally,
C
0
and C
1
are represented as follows.
C
0
= {matrices obtained by permuting the columns of
B
0
=
p
0
0,0
p
0
0,1
... p
0
0,l−1
.
.
.
p
0
n−1,0
p
0
n−1,1
... p
0
n−1,l−1
},
C
1
= {matrices obtained by permuting the columns of
B
1
=
p
1
0,0
p
1
0,1
... p
1
0,l−1
.
.
.
p
1
n−1,0
p
1
n−1,1
... p
1
n−1,l−1
},
where p
0
i, j
, p
1
i, j
∈ {0,1} for 0 ≤ i ≤ n − 1 and
0 ≤ j ≤ l − 1.
Due to the page limitation, we refer readers to
(Naor and Shamir, 1994) for details of the represen-
tation. In the next section, we use a black-and-white
VCS described above as a building block to build a
k-out-of-n color EVCS which does not have pixel ex-
pansion. Note that the pixel expansion rate of the
VCS above is l > 1.
3 OUR K-OUT-OF-N EVCS FOR
COLOR IMAGES
We now propose a k-out-of-n EVCS for color images.
The scheme is the first EVCS for color images with
no pixel expansion. For a color secret image, suppose
that n meaningful images have already been chosen.
These images are color images chosen arbitrarily and
will be used for generating n share images. Also, the
choosing processing is totally independent as long as
the image size is the same as that of the secret image
since our scheme does not have any pixel expansion.
Our scheme consists of the following steps: 1. His-
togram Generation; 2. Color Quality Determination;
3. Grouping; 4. Share Creation. These steps are elab-
orated in detail as follows.
3.1 Histogram Generation
For the secret image and each of the n images which
will be used as share images, we first generate three
primary-color (i.e. R, G, B) component images for
each of them and then create a histogram for each
primary-color component image. As an example,
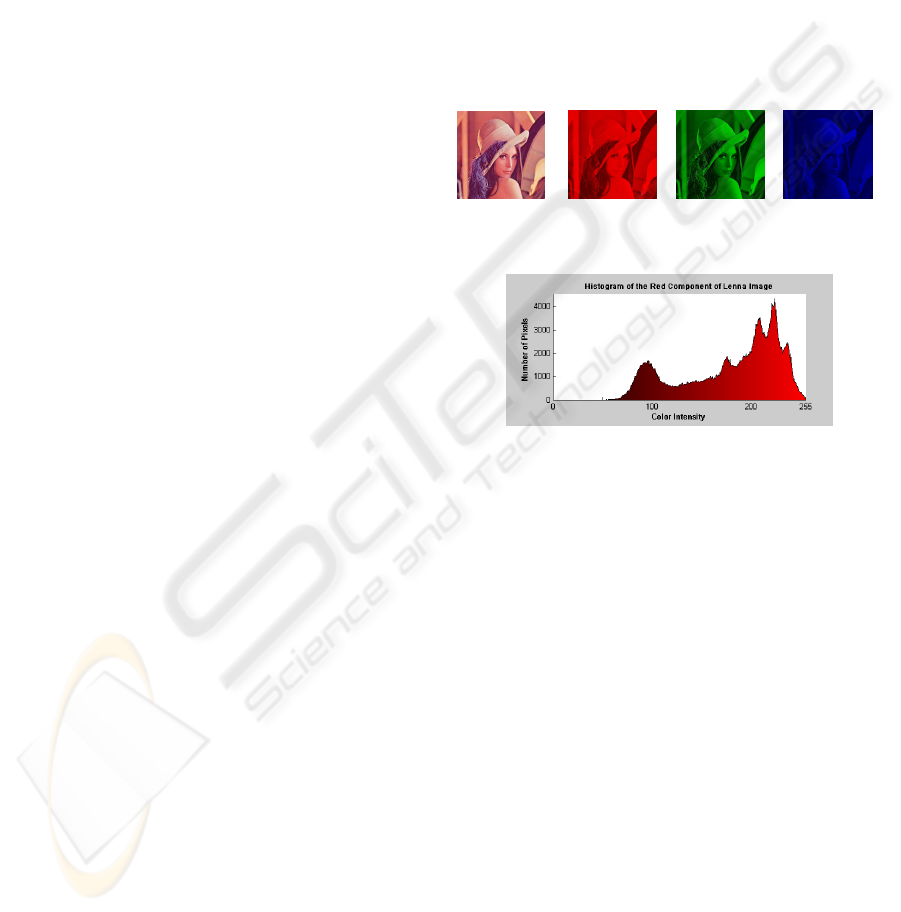
suppose that the secret image is the Lena image which
is encoded in 24-bit RGB. Figure 1 shows the secret
image (Lena) and the three RGB primary-color com-
ponent images of it. In each component image, there
are 256 levels of intensity of the corresponding pri-
mary color. Figure 2 shows the histogram of the red
component generated in this step. In the histogram of
R (resp. G and B), the horizontal axis represents the
intensity of R (resp. G and B) ranging from 0 to 255
and the vertical axis represents the number of pixels
in the R (resp. G and B) component image that have
the intensity value.
Figure 1: The secret image (Lena) and its RGB component
images.
Figure 2: Histogram of the red component image.
3.2 Color Quality Determination
In this step, the user is to choose the number of in-
tensity levels that the reconstructed image will have
when at least k share images are superimposed and
the number of intensity levels of each share image.
First, the user is to determine the number of intensity
levels for maximizing the quality of the reconstructed
image or shares. Let N be the number of intensity
levels that the reconstructed image will have. As the
reconstructed image has three primary-color compo-
nents, we set N = N
R
× N
G
× N
B
, where N
X
denotes
the number of the intensity levels of X ∈ {R,G,B}
primary-color component of the reconstructed image.
For the n share images, let M
i
be the number of in-
tensity levels of the i-th share image (for i = 1, ...,n),
where M
i
= M
i
R
× M
i
G
× M
i
B
, where M
i
X
denotes the
number of intensity levels of X ∈ {R, G,B} compo-
nent of the i-th share. In Sec. 4, we provide more dis-
cussions on how to choose the number of color levels.
SECRYPT 2010 - International Conference on Security and Cryptography
424
3.3 Grouping
As of the previous step, this step is carried out on each
of the n share images as well as the secret image. In
the following, we use the secret image as an example
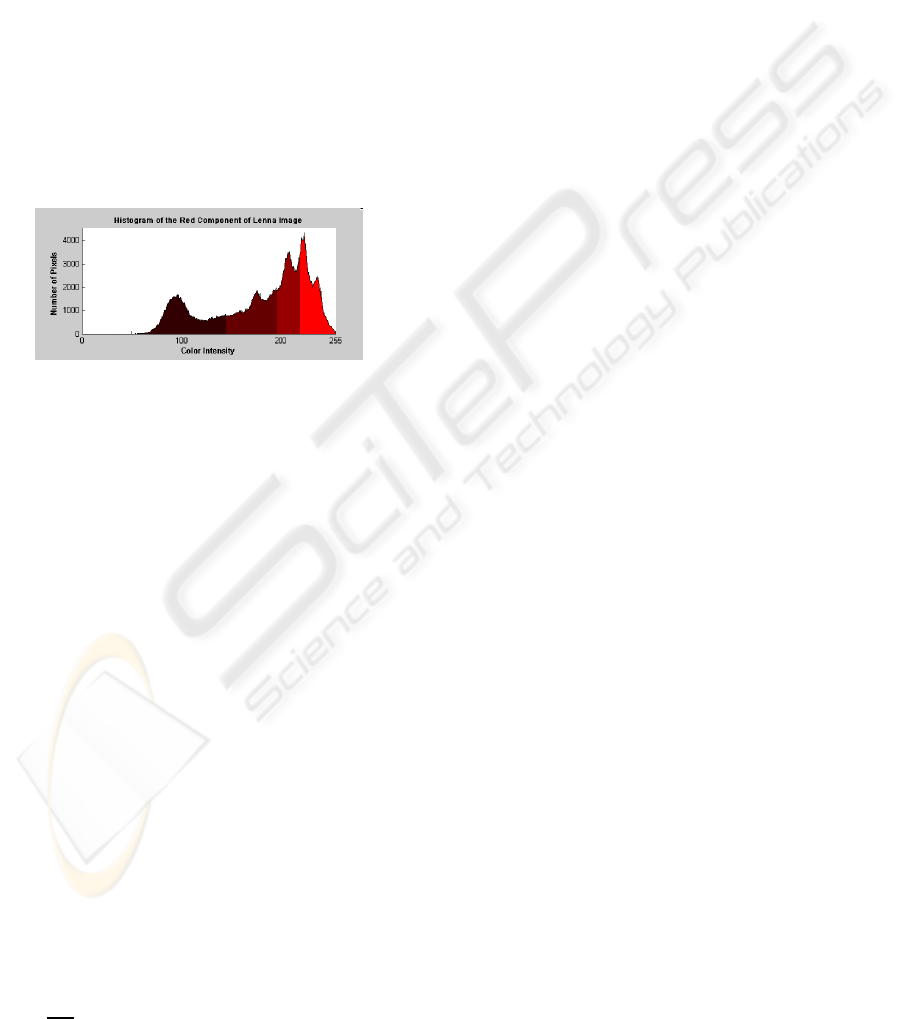
to describe how the grouping works. For each pri-
mary color X ∈ {R,G,B}, we partition the histogram
of X of the secret image into N
X
groups so that each
group has the same area as other groups on the his-
togram, where N
X
is the number of color intensities
for the X component of the (to-be)-reconstructed se-
cret image determined in the previous step. By the
same area on a histogram, it implies that there will be
an equal number of pixels in each of the N
X
groups
on the histogram. Figure 3 shows the histogram of
the red primary-color component images of Lena af-
ter grouping where N
R
= 4 . In the figure, we use dif-
ferent color intensities to represent different groups.
Figure 3: Histogram of R illustrating the 4 × 4 × 4 color
levels.
3.4 Share Creation
The final step of the scheme is to create the n share
images. To create these shares, we start with by cre-
ating n shares for each primary color. After creating
all the shares of the three primary colors, we then su-
perimpose the three shares corresponding to the three
primary colors of the i-th share, 1 ≤ i ≤ n, for forming
the n final shares. In the following, we describe how
the n shares of each primary color X ∈ {R, G,B} are
created.
1. We first construct a k-out-of-n black-and-white
EVCS. The construction can be viewed as an ex-
tension of the k-out-of-n black-and-white VCS re-
viewed in Sec. 2. The extension is similar to
the method due to Wang, Yi and Li (Wang et al.,
2009).
(a) Take a k-out-of-n black-and-white VCS which
satisfies the conditions in Sec. 2. Let the Basic
Matrices B
0
and B
1
are of dimension n× l.
(b) Then, we construct 2
n
boolean matrices de-
noted by A
c
1
,...,c
n
for c
1
,... ,c
n
∈ {b,w}, where
b stands for black and w stands for white. Each
of A
c
1
,...,c
n
will be n × t for some integer t ≥
⌈
n
k−1
⌉. In each row of A
c
1
,...,c
n
, for example, the
i-th row, all the t bits but one must be 1. The
remaining bit is 1 if c
i
= b and is 0 if c
i
= w.
We denote this bit as ∗ in the following. In
other words, each row of A
c
1
,...,c
n
has only one
∗. Besides, the number of ∗ in each column of
A
c
1
,...,c
n
should be at most k−1.
(c) The k-out-of-n black-and-white EVCS is de-
fined as the following Basic Matrices:
T
c
1
,...,c
n
0
= B
0
◦ A
c
1
,...,c
n
and T
c
1
,...,c
n
1
= B
1
◦
A
c
1
,...,c
n
for c
1
,... ,c
n
∈ {b,w}. Therefore,
there are altogether 2
n+1
Basic Matrices and
they can be considered as two sets of Ba-
sic Matrices, that is, {T
c
1
,...,c
n
0
}
c
1
,...,c
n
∈{b,w}
and
{T
c
1
,...,c
n
1
}
c
1
,...,c
n
∈{b,w}
, each set has 2
n
Basic
Matrices. Each of these matrices is n× m where
m = l +t where B
0
and B
0
are n× l and A
c
1
,...,c
n
are n×t. We refer readers to (Wang et al., 2009)
for the details of how this k-out-of-n black and
white EVCS works.
In the next step, we use the Basic Matrices
T
c
1
,...,c
n
0
and T
c
1
,...,c
n
1
in a probabilistic way on
each RGB primary-color component image so
that the share images created will have the same
size as the original secret image (i.e. no pixel
expansion or having the optimal pixel expan-
sion rate of 1).
2. This step is carried out pixel by pixel for the se-
cret image. For each primary color X ∈ {R,G, B}
of a pixel in the secret image, we carry out the
following steps:
(a) On the X histogram of the secret image, sup-
pose that the color intensity of the pixel with
respect to primary color X is in the k-th group
(where 0 ≤ k ≤ N
X
− 1). We compute a proba-
bility value P
X
= k/(N
X
− 1) which determines
the likelihood of going through one of the fol-
lowing steps.
(b) With probability P
X
, we carry out the following
two steps:
• We look into n × l Basic Matrix B
0
of the k-
out-of-n black-and-whiteVCS and the general
form A
c
1
,...,c
n
.
– With probability P
1
, which is determined by
the user as follows, we randomly pick a col-
umn from B
0
; The trade-off between the
quality of share images and the reconstructed
image is the result of adjusting the value of
P
1
. The greater (less) the P
1
is, the higher
(lower) the quality of the reconstructed im-
age would be and the lower (higher) the qual-
ity of the share images would be.
– With probability 1 − P
1
, suppose the color
intensity of the X primary-color component
EXTENDED VISUAL CRYPTOGRAPHY SCHEME FOR COLOR IMAGES WITH NO PIXEL EXPANSION
425

of the corresponding pixel in the i-th mean-
ingful image is in the k
i
X
-th group (where
0 ≤ k
i
X
≤ M
i
X
− 1 and 1 ≤ i ≤ n), we com-
pute a probability value Q
i
X
= k
i
X
/(M
i
X
−1).
We then set the ∗ in the i-th row of the gen-
eral form A
c
1
,...,c
n
to 0 with the probability
Q
i
X
and to 1 with the probability 1-Q
i
X
and
randomly choose a column from it.
• Consider the column chosen as an n-bit vec-
tor. For the first bit, we assign the black color
(i.e. 0 color intensity) if the bit is 1, otherwise
we assign X primary color (i.e. 255 color in-
tensity) to the correpsonding pixel in the first
share image. This continues until we have as-
signed colors to the corresponding pixel on all
the n share images.
(c) With the probability 1− P, we carry out similar
steps to the above, but change B
0
to B
1
.
3. Finally, we superimpose the i-th R share with the
i-th G share and the i-th B share, for i = 1,...,n,
to form the final i-th color share image.
4 DETERMINING THE NUMBER
OF COLOR LEVELS
In this section, we discuss how to choose the number
of color levels (i.e. N = N
R
× N
G
× N
B
) in the recon-
structed secret image and the share images. As the
scheme allows a user to arbitrarily choose the number
of color levels, we observe that the number of color
levels has a significant impact on the quality of the
reconstructed image and the share images. The num-
ber of color levels should be chosen depending on the
number of colors of the original n+ 1 images. In the
following, we take the reconstructed image as an ex-
ample.
We first identify the secret image as belonging to
one of the following two categories: in category 1, the
number of levels of a particular primary color is small,
for example, less than 4; and in category 2, the num-
ber is large, say at least 4. For images in category 1, if
the image on a particular primary color X ∈ {R,G, B}
is OriginalN
X
, since OriginalN
X
in this case is small,
there is no need to try with different color levels. We
should just set N
X
to OriginalN
X
. Images that fall into
this category could be texts or logos. Figure 4 and
Figure 5 show the images of text, their corresponding
shares and the reconstructed image (Lena) for the case
of 2-out-of-2 EVCS, N
R
= N
G
= N
B
= M
i
R
= M
i
G
=
M
i
B
= 2 (where i = 1,2).
For images in category 2, one may try the color
level N
X
from a small value, say 2 or 4, to the “full”
Figure 4: The images of the text.
Figure 5: The two shares and the reconstructed image of the
text.
level, i.e. OriginalN
X
. Based on our experimental
results, we observe that for photos or color cartoon
images with large number of color levels, trying these
three values (namely 2, 4 or OriginalN
X
) for the value
of N
X
can already attain one of the best results in the
reconstructed images.
REFERENCES
Ateniese, G., Blundo, C., Santis, A. D., and Stinson, D. R.
(1996). Visual cryptography for general access struc-
tures. Inf. Comput., 129(2):86–106.
Nakajima, M. and Yamaguchi, Y. (2002). Extended visual
cryptography for natural images. Journal of WSCG,
10(2):303–310.
Naor, M. and Shamir, A. (1994). Visual cryptography. In
Advances in Cryptology - EUROCRYPT ’94, pages 1–
12. Lecture Notes in Computer Science, Vol. 950.
Sirhindi, R., Afzal, M., and Murtaza, S. (2009). An ex-
tended secret sharing scheme for colour images with
fixed pixel expansion. International Journal of Elec-
tronic Security and Digital Forensics, 2(1):58–67.
Wang, D., Yi, F., and Li, X. (2009). On general construc-
tion for extended visual cryptography schemes. Pat-
tern Recognition, 42(11):3071–3082.
Yang, C. N. (2004). New visual secret sharing schemes us-
ing probabilistic method. Pattern Recognition Letters,
25(4):481–494.
SECRYPT 2010 - International Conference on Security and Cryptography
426
