
CONFIDENTIALITY AND INTEGRITY FOR SUM AGGREGATION
IN SENSOR NETWORKS
Keith B. Frikken and Yihua Zhang
Miami University, Oxford, Ohio, U.S.A.
Keywords:
Sensor aggragation, Privacy, Integrity.
Abstract:
When deploying sensor networks in environments that monitor people (e.g., monitoring water usage), both
privacy and integrity are important. Several solutions have been proposed for privacy (Castelluccia et al.,
2005), (He et al., 2007), and integrity (Yang et al., 2006), (Przydatek et al., 2003), (Hu and Evans, 2003), (Chan
et al., 2006), (Frikken and Dougherty, 2008). Unfortunately, these mechanisms are not easily composable. In
this paper, we extend the splitting schemes proposed in (He et al., 2007) to provide privacy and integrity when
computing the SUM aggregate. Our scheme provides privacy even if the base station colludes with some
cluster heads, and provides integrity by detecting when individual nodes inflate or deflate their values too
much. Our main contributions are: i) a new integrity measure that is a relaxation of the one in (Chan et al.,
2006), ii) a new privacy measure called k-similarity, iii) a construction that satisfies both of these measures for
the computation of the SUM aggregate that avoids the usage of expensive cryptography, and iv) experimental
results that demonstrate the effectiveness of our techniques.
1 INTRODUCTION
Wireless sensor networks have promising applica-
tions from military surveillance to civilian usage. In
these applications, the base station queries the net-
work and sensor nodes report their values to the base
station. In some applications, privacy and integrity
are security concerns. For example, if the sensor’s
individual readings reveal information about specific
people, then these values must be protected (even
against the base station). Furthermore, as individual
nodes may become compromised the base station de-
sires a guarantee about the accuracy of the query re-
sult.
A well known technique to extend the lifetime
of the network is in-network aggregation. Although
this approach reduces the communication overhead
and extends the network’s operation time, in its most
straight-forward implementation it suffers from both
privacy and integrity problems (for a detailed survey
of security in aggregation see (Alzaid et al., 2008)).
In terms of privacy, while the base station only re-
ceives an aggregated result, the values are now leaked
to other nodes(i.e., aggregator nodes) in the network.
Also, there are now two integrity threats: i) a node
may inflate of deflate its values (and the base station
can no longer perform the sanity check on each value)
and ii) an aggregator might misrepresent the aggre-
gated value. There has been a significant amount of
work (Castelluccia et al., 2005) and (He et al., 2007)
addressing the privacy issue for in-network aggrega-
tion. However, all of these works assume that sen-
sors will honestly report their values. Also, many
schemes (Yang et al., 2006), (Przydatek et al., 2003),
(Hu and Evans, 2003), (Chan et al., 2006), (Frikken
and Dougherty, 2008) address the integrity issue. Ba-
sically, these schemes use other nodes to verify the
validity of reported values. However, with these ap-
proaches a verifying node inevitably learns the sen-
sitive information for the nodes that it verifies. The
natural question becomes “Can we design a scheme
that achieves both privacy and integrity?” The only
work that we are aware of that addresses both of these
problems is (Roberto et al., 2009) and (Castelluccia
and Soriente, 2008). We discuss the differences be-
tween our work and this prior work in the next sec-
tion.
We propose a scheme for computing the sum ag-
gregate that provably achieves both meaningful pri-
vacy and integrity. Our work is built upon the
SMART scheme(He et al., 2007), that uses the split-
and-merge mechanism. Our main contributions are:
1. We introduce the notion of amplification factor
to measure the deviation degree between the re-
231
B. Frikken K. and Zhang Y. (2010).
CONFIDENTIALITY AND INTEGRITY FOR SUM AGGREGATION IN SENSOR NETWORKS.
In Proceedings of the International Conference on Security and Cryptography, pages 231-240
DOI: 10.5220/0002937602310240
Copyright
c
SciTePress

ported and the correct aggregate values.
2. We introduce a new privacy notion, k-similarity,
that provides “good” enough security. We provide
analysis to show that this new notion provides a
reasonable level of privacy.
3. We provide a protocol for computing the sum ag-
gregate that achieves both integrity and privacy.
The proofs of these claims is omitted due to page
constraints. Expensive cryptography is not used in
this protocol, which makes it applicable to current
sensor technology. Furthermore, the communica-
tion is also reasonable.
4. We provide experimental results to demonstrate
the effectiveness of our approach.
The rest of this paper is organized as follows: in
section 2 we survey related literature. In section 3 we
define the problem, and in section 4 we introduce a
splitting scheme that performs the sum aggregation.
In section 5, we formally define the integrity and pri-
vacy goals for splitting schemes. In section 6, we pro-
vide a construction that satisfies our goals. In section
7, a series of experiments to test the effectiveness of
our constructions is performed. Finally in section 8,
we summarize our work and describe future work.
2 RELATED WORK
Initial works(Madden et al., 2002), (Intanagonwiwat
et al., 2002) in the data aggregation domain share the
same assumption that all sensors in the network are
honest, and no outsiders attempt to eavesdrop or tam-
per with the sensor readings. However, in reality, sen-
sors are deployed in unattended or hostile environ-
ments which put them at risk in the following ways: i)
adversaries interested in the values of individual sen-
sors will either eavesdrop the communication or phys-
ically crack the sensors to obtain the sensor readings
and ii) adversaries who compromise a fraction of sen-
sors will attempt to mislead the base station to accept
a spurious aggregate result or prevent the final aggre-
gate from being reported to the base station. Many
schemes have been introduced that address either the
privacy or the integrity issue.
Many of the approaches for integrity utilize
a divide-and-conquer, commit-and-attest mechanism
for the purpose of obtaining an acceptable aggre-
gation result when a fraction of sensors are com-
promised. These schemes fail to achieve privacy,
because in the aggregation phase, the intermediate
node(aggregator) will learn all private sensor read-
ings sent from its children. In (Chan et al., 2006) and
(Frikken and Dougherty, 2008), schemes for provably
secure hierarchical in-network data aggregation were
proposed. The schemes were based on a commit-and-
attest mechanism, but utilized the delayed aggrega-
tion to effectively reduce the verification overhead.
However, neither of these schemes provided privacy.
Works presented in (Castelluccia et al., 2005),
(He et al., 2007) are related to privacy preservation.
In (Castelluccia et al., 2005), the author proposed a
homomorphic encryption scheme that achieves both
the end-to-end privacy and energy-efficient proper-
ties. Another work (He et al., 2007) introduced two
schemes(CPDA, SMART) to protect individual sen-
sor readings during the aggregation phase. Specifi-
cally, in the SMART scheme each sensor conceals its
private data by slicing it into pieces, and sends the
pieces to different cluster heads in the networks. Af-
ter receiving all shares, those cluster heads will sim-
ply aggregate those shares, and further send the ag-
gregate to the base station. One major problem in
these two works(Castelluccia et al., 2005), (He et al.,
2007) is that they did not consider the existence of
malicious users who may report illegal values (e.g.,
values that are outside of the range of legal values).
Lacking a mechanism to check the validity of reported
values, the integrity will not be guaranteed. Our work
is primarily based on analyzing the security charac-
teristics of the SMART scheme, and aims to incor-
porate both the confidentiality and integrity into this
scheme. Source location privacy(Kamat et al., 2005),
(Yang et al., 2008) attempts to hide the location of
a reported event, which is an orthogonal issue to the
issues considered in this paper.
Recently, a scheme(Roberto et al., 2009) was pro-
posed to address both of the privacy and integrity is-
sues. In (Roberto et al., 2009), the author applies ho-
momorphic encryption to preserve the privacy, and
uses monitoring sensors to detect the abnormal be-
havior of aggregators. That is, each aggregating node
has several monitoring nodes that ensure that the ag-
gregator does not misbehave. However, this does not
prevent leaf nodes from intentionally reporting ille-
gal values. In order to preserve privacy, the scheme
also requires that neither the aggregating nodes nor
the monitoring nodes collude with the base station.
Another scheme, ABBA, (Castelluccia and Sori-
ente, 2008) was proposed for providing privacy and
integrity in sensor aggregation which utilized an addi-
tive checksum to provide integrity. A downside with
this approach was that if an adversary corrupted a sin-
gle node and knows the reported values of several
nodes in the network, then this adversary can modify
these known values to arbitrary values.
SECRYPT 2010 - International Conference on Security and Cryptography
232

3 PROBLEM DEFINITION
We consider a sensor network with N nodes, denoted
by s
1
,...,s
N
. At any given time each sensor node
has a value in the range [0,M], where node s
i
’s value
is denoted by v
i
. A special node, the base station,
will query the network to learn
∑
N
i=1
v
i
. Limiting the
range of values to [0,M] does not limit the applicabil-
ity of the scheme, because other ranges can simply be
scaled to match this type of range.
We assume that there is a special set of nodes,
called cluster heads. These cluster heads could ei-
ther be more expensive tamper-resistant nodes, or can
be regular nodes in the network that are identified via
a cluster formation process (as in (He et al., 2007)).
During deployment (before the adversary compro-
mises nodes), each sensor node discovers its closest C
cluster heads. The regular nodes in the network will
send information to their closest cluster heads, and
then these cluster heads will pass the aggregation in-
formation up the aggregation tree to the base station.
We assume that sensor nodes have keys with each
other. Specifically, we require that each sensor node
has a key with each of its C cluster heads. This can be
achieved using one of the many well-known key pre-
distribution schemes (see (Camtepe and Yener, 2005)
for a survey of such schemes). We assume that the
base station can perform authenticated broadcast by
using a protocol such as µTELSA(Perrig et al., 2002).
The primary security concerns in this paper are:
1. Integrity. We want to defend against the stealthy
attack defined in (Przydatek et al., 2003). Specif-
ically, we assume that some leaf nodes are com-
promised, and we want to prevent them from con-
vincing the base station of a false result. At a high
level, we want to prevent nodes from being able
to have more influence on the final aggregate than
what can be achieved by changing its reported
value to something in the range [0,M]. We achieve
only a weakened form of this goal. Essentially,
we bound the amount that each node cannot in-
fluence the result. When using in-network aggre-
gation, there are two potential threats: i) a sens-
ing node is corrupt and reports a value outside of
the range [0, M], and ii) aggregating node modi-
fies the results of previous nodes. The scheme in
(Chan et al., 2006) protected against both of these
threats, but did not preserve privacy. The work
in (Roberto et al., 2009) did not consider the first
type of attack, and thus to corrupt the result, an
adversary only needs corrupt an individual node.
In this paper we focus on preventing this type
of attack, but do not address corrupt aggregating
nodes. However, our techniques can be combined
with the technique in (Roberto et al., 2009) to pro-
tect against both corrupt reporting nodes and cor-
rupt aggregating nodes.
2. Privacy. The value of each sensor node should
be private, even from the base station. We assume
that the base station and up to t cluster heads are
corrupt, and attempt to learn an individual sen-
sor’s values. Here “corrupt” means that the clus-
ter heads collude with the base station to reveal
the sensor’s private data, not that it lies to the
base station(i.e., misrepresent the sensor’s private
reading, or not warn the base station about illegal
shares). We prove security when t = 1, but pro-
vide experimental results that show that our ap-
proach is effective for larger t values.
3. Availability. We do not consider denial of service
attacks in this paper.
4 SUM AGGREGATION USING
SPLITTING SCHEMES
In this section, we will review the basic ideas of the
SMART (He et al., 2007) splitting scheme that aims
to preserve the privacy of each sensor’s reading dur-
ing the sum aggregation. Each sensor hides its private
data by slicing it into several pieces, and then it sends
each encrypted piece to different cluster heads. After
receiving all pieces, each cluster head will calculate
the intermediate aggregate result, and further report
it to the base station. To explain in details, we will
divide this process into three steps: Slice, Mix and
Merge.
Step 1 (“Slice”). Each node s
i
, will slice v
i
into
C shares: v
1
i
,...,v
C
i
. That is v
i
=
∑
C
j=1
v
j
i
. The node
then sends to each of its C cluster heads one of these
values.
Step 2 (“Mix”). After receiving all of the shares,
the cluster head decrypts all of its values and sums up
all of the reported shares. It then sends this aggregate
to the base station.
Step 3 (“Merge”). The base station receives all
of the values from the cluster heads and sums up all
of these values to obtain the sum of all nodes’ values.
This value will be
∑
N
i=1
∑
C
j=1
v
j
i
=
∑
N
i=1
v
i
.
It is important to note that the actual SMART pro-
tocol is slightly different from the one above. Specif-
ically, each node would sends their shares to a ran-
dom subset of nodes in the network. Also, the nodes
keep one share for themselves, aggregate it with other
shares it received. While the SMART protocol in-
tuitively achieves private aggregation for the SUM,
there are two main limitations to its initial presenta-
CONFIDENTIALITY AND INTEGRITY FOR SUM AGGREGATION IN SENSOR NETWORKS
233

tion in (He et al., 2007). First, no description of how
to split the values was given in (He et al., 2007), and
second, no formal analysis was given to provide any
security guarantees. However, this approach does po-
tentially enjoy an additional advantage that was not
discussed in (He et al., 2007); specifically, it can po-
tentially provide integrity in addition to privacy. That
is, in the mixing step, the cluster heads can verify that
the values are in a valid range; and thus, this could
bound the amount a corrupted node can affect the fi-
nal aggregate. The aims of this paper are to: i) give a
specific construction for splitting schemes, ii) provide
a formal analysis of the effectiveness of this scheme
with regards to privacy and integrity, and iii) demon-
strate that the construction provides a meaningful no-
tion of privacy and integrity.
5 FORMALIZING SPLITTING
SCHEMES
In this section we formalize the desired properties of
a splitting scheme, so that it can be used in a proto-
col such as the one in the previous section to provide
integrity and privacy. Suppose a sensor node has a
value v that is in the range [0,M]. The node is con-
cerned about the privacy of v so it splits v into inte-
ger shares v
1
,...,v
s
such that
∑
s
i=1
v
i
= v. The node
then reports to each of its cluster heads one of these
values. The cluster heads then verify that each share
is in a valid range and then aggregate the individual
shares. The privacy concern with this approach is that
an adversary would obtain some share values (i.e., by
corrupting some cluster heads) and then be able to de-
termine information about v. Informally, the goal is
that if the adversary obtains up to some threshold t
shares, the adversary should not be able to determine
the value used to generate the shares. In the remainder
of this section we focus on the case where t = 1, but
in section 7 we consider larger values of t. What com-
plicates this problem, is the orthogonal server goal of
data integrity; that is the server wants to prevent the
client from inflating or deflating his value too much
(i.e., reporting a value outside of the range [0,M]. We
now formalize some notions about splitting values.
Definition 1. A splitting scheme is a probabilistic al-
gorithm S that takes as input: i) an upper bound on
values M, ii) a value v ∈ [0, M], and iii) a number of
shares s. S then produces output v
1
,...,v
s
such that
∑
s
i=1
v
i
= v.
To simplify the analysis of splitting schemes we
will consider only splitting schemes where the distri-
bution for share v
i
is the same as the distribution for
the share v
j
for all i, j ∈ [1,s]. More formally:
Definition 2. A splitting scheme, S, is called symmet-
ric if ∀i
1
,i
2
∈[1,s] and j ∈Z, Pr[v
i
1
= j|(v
1
,...,v
s
) ←
S(M, v,s)] = Pr[v
i
2
= j|(v
1
,...,v
s
) ← S(M,v,s)] for
all valid choices of M, v, and s.
One may be concerned that asymmetric splitting
schemes may perform better than symmetric splitting
schemes. However, suppose we have an asymmetric
splitting scheme, A. To convert A into a symmetric
scheme: i) compute (v
1
,...,v
s
) ← A(M, v, s) and ii)
randomly permute the shares to obtain the respective
shares. It is straightforward to show that this a sym-
metric scheme, and clearly if no t shares reveal any-
thing about v in the original set, then no t shares reveal
anything about v in the permuted set. Thus it suffi-
cient to consider only symmetric splitting schemes.
5.1 Integrity Goal
The server’s integrity concern is that a corrupted sen-
sor may report a value not in the range [0,M]. Any
splitting scheme will produce shares inside of a spe-
cific range, we call the range [Min,Max]. Formally,
Definition 3. The range of a splitting scheme, a
share count s and an upper bound M is denoted by
range(S,M, s) is [Min(S,M, s), Max(S,M, s)] where
• Min(S,M, s) (resp. Max(S, M,s)) is the mini-
mum (resp. maximum) share value produced by
S(M, v,s) over all possible v ∈ [0,M] and all pos-
sible choices for the randomness for S.
Since individual cluster heads know the value
range(S,M,s), they can verify that the shares that it
receives are inside this range. If any of the shares are
outside this range, then the cluster head reports the
error to the base station. Thus a node can cannot re-
port any value outside of the range [s ×Min(S,M,s),
s ×Max(S,M, s)] to the base station. The additional
range reporting capability is defined in the following
metric:
Definition 4. The amplification factor of a splitting
scheme S for parameters M,s is
s ×Max(S,M, s) −s ×Min(S,M, s) + 1
M + 1
As an example, suppose that the user’s values
must be in the range [0,2], and that the splitting
scheme produces two shares each in the range [−2,2].
Thus a malicious node can report any value in the
range [−4,4], and so the amplification factor is 3, that
is a malicious user can report a value in a range that is
three times bigger than the range of the actual values.
That is, if the splitting scheme has an amplification
SECRYPT 2010 - International Conference on Security and Cryptography
234

factor of a, then compromising a single node is like
compromising a nodes in a scheme where all reported
values are to be in the range [0,M].
Clearly, the goal is to make the amplification fac-
tor as close to 1 as possible. In fact, in the absence of
the privacy goal, this is trivial. Simply have s = 1, and
have S(M, v,s) = v. However, while this provides am-
plification factor of 1, it clearly provides no privacy.
5.2 Privacy Goal
The initial privacy goal is that the adversary should
not be able to determine the value of the result, when
given one of the shares. Since the scheme is symmet-
ric we only consider giving the first share to the adver-
sary (that is the first share has the same distribution as
every other share, so the adversary will not gain more
information from receiving a different share). We for-
malize this notion for symmetric splitting schemes in
the following experiment:
Definition 5. Share Indistinguishability Experi-
ment Exp
M,s,S
A
(k).
1. A is given the security parameter 1
k
, the values M
and s. A chooses two values m
0
and m
1
(both in
[0,M]).
2. A bit b is randomly chosen. (v
1
,...,v
s
) ←
S(M, m
b
,s). A is given v
1
.
3. A outputs a bit b
0
.
4. If b = b
0
, then output 1. Otherwise output 0.
We denote the advantage of A as Adv
M,s,S
A
(k) :=
Pr[Exp
M,s,S
A
(k) = 1] −
1
2
. We say that a split-
ting scheme is cryptographically private if for all
probabilistic polynomial time (PPT) algorithms A,
Adv
M,s,S
A
(k) is negligible in k. Here, “negligible” has
the standard cryptographic definition. That is, a func-
tion f (k) is negligible if for all polynomials P and
large enough N: ∀n > N : f (n) <
1
P(n)
.
If we ignore the integrity goal, then it is straight-
forward to achieve cryptographic privacy. Essentially,
the algorithm chooses v
1
uniformly from [0,M ∗2
k
]
and sets v
2
= v −v
1
. We omit a formal proof that this
is cryptographically private, but the basic idea is that
if v
1
is chosen in the range [M, (2
k
−1)M], then no in-
formation is leaked about v, by either of the individual
shares. v
1
is not chosen in this range with probability
(2M)/M2
k
=
1
2
k−1
, which is negligible in k. Unfor-
tunately, this scheme has an amplification factor of
2
k+1
, which clearly provides no meaningful integrity.
5.2.1 Good Enough Privacy
As can be seen from the previous two sections, it is
possible to achieve either integrity or cryptographic
privacy for splitting schemes. The natural question
that arises is whether it is possible to achieve both
simultaneously. Unfortunately, we later show that
any splitting scheme with cryptographic privacy has
super-polynomial (in terms of the security parameter)
amplification factor. This implies that one of the two
constraints must be weakened. In order for a split-
ting scheme to provide any integrity, the amplification
factor must be kept small, and thus the question be-
comes: “Is there a meaningful notion of privacy that
can be obtained that suffers only moderate amplifica-
tion factor?” In the remainder of this section we first
prove the impossibility result, describe some failed at-
tempts at privacy, and then introduce and analyse a
new notion of privacy called k-similarity.
5.2.2 Impossibility Result
We now show that a symmetric splitting scheme
cannot achieve both cryptographic privacy and
polynomially-bounded amplification factor. Due to
page constraints we omit the formal proof and give
only a sketch of the results below. Specifically, the
main result is as follows:
Theorem 1. Any symmetric splitting scheme, S, with
parameters M, and s (s > 1) such that Adv
M,s,S
A
(k) ≤ε
has an amplification factor ≥
√
Ms
2(M+1)
√
ε
A consequence of the above theorem is that if the
adversary advantage is negligible in k, then the ampli-
fication factor must be super-polynomial. That is, M
and s are fixed constants, and the ε is in the denomi-
nator, so the amplification factor is inversely propor-
tional to the square root of the adversary advantage.
Before sketching the proof, we define the follow-
ing notation:
Definition 6. A symmetric splitting scheme, S for
range [0, M] and shares s induces a distribution on
[Min(S, M,s), Max(S,M, s)]for each value v ∈ [0,M].
We denote the probability that a share is i given a split
value v as:
D
S,M,s
v
[i] = Pr[v
1
= i|(v
1
,...,v
s
) ← S(M,v,s)].
Theorem 1 rests on the following two lemmas:
Lemma 1.
∑
Max(S,M,s)
i=Min(S,M,s)
i ∗D
S,M,s
v
[i] =
v
s
.
Lemma 2. Suppose ∃i ∈ [Min(S,M, s), Max(S,M, s)]
and m
0
,m
1
∈ [0, M] such that |D
S,M,s
m
0
[i] −D
S,M,s
m
1
[i]| ≥
ε, then there exists a PPT adversary A such that
Adv
M,s,S
A
(k) ≥
ε
4
.
The proof proceeds as follows, using lemma 1
it is possible to show that when splitting two dif-
ferent values that there is a specific value where
CONFIDENTIALITY AND INTEGRITY FOR SUM AGGREGATION IN SENSOR NETWORKS
235
the value is above
M
(r−1)s
(where r = Max(S,M,s) −
Min(S, M,s) + 1) . However, combining this with
Lemma 2 this is enough to show unless r is super-
polynomial, that the Adv
M,s,S
A
(k) is non-negligible.
5.2.3 A Definition for Privacy
Clearly, in order for splitting schemes to be useful, we
need to relax one of our two goals. If we require cryp-
tographic privacy, then the amplification factor will be
large and no useful integrity will be provided. Thus
we explore weaker definitions of privacy; our funda-
mental goal is to place some bound on the information
gained by an adversary. Before describing the defini-
tion, we look at some failed attempts:
1. We could require that |D
S,M,s
m
0
[i] −D
S,M,s
m
1
[i]| is be-
low some threshold ε for all values m
0
, m
1
, and i.
However, this does not prevent the following situ-
ation: D
S,M,s
m
0
[i] = 0 and D
S,M,s
m
1
[i]| 6= 0. If this situ-
ation happens, and the adversary is attempting to
distinguish between m
0
and m
1
and the corrupted
sample is i, then the adversary is certain that the
split value is m
1
. Thus the adversary’s knowledge
gain is potentially arbitrarily large.
2. A stronger condition is that
∑
Max(S,M,s)
i=Min(S,M,s)
|D
S,M,s
m
0
[i]
−D
S,M,s
m
1
[i]| is below some threshold ε. However,
this has the same problem as the prior approach.
When considering the amount of knowledge
gained from a share, an important factor is that the
difference between the two distributions at any point
is small relative to the values at those points. Using
this as motivation we propose the following defini-
tion.
Definition 7. A symmetric splitting scheme, S,
with parameters M, and s provides k-similar
privacy if and only if ∀m
0
,m
1
∈ [0,M], ∀i ∈
[Min(S, M,s),Max(S, M,s)] either
i) D
S,M,s
m
0
[i] = 0 and D
S,M,s
m
1
[i] = 0 or
ii)
min{D
S,M,s
m
0
[i],D
S,M,s
m
1
[i]}
max{D
S,M,s
m
0
[i],D
S,M,s
m
1
[i]}−min{D
S,M,s
m
0
[i],D
S,M,s
m
1
[i]}
≥ k
5.2.4 Analysis of k-similar Privacy
We are interested in bounding the “information gain”
that the adversary has from the captured share. To
model this, suppose that the adversary is trying to dis-
tinguish whether the user has a value m
0
or a value
m
1
. Furthermore, the adversary has some background
knowledge regarding the likelihood that the value is
m
0
, and we represent this as probability P. We stress
that we do not assume knowledge of value P, but
rather we wish bound the information gain for any
value of P. Denote as P
i
the adversary’s probabil-
ity that the value is m
0
after seeing a single sample
with value i. Below, a bound is placed upon the value
|P
i
−P|, which is independent of i.
Theorem 2. If a splitting scheme satisfies k-
similarity, then |P
i
−P|≤
Q−Q
2
Q+k
where Q =
√
k
2
+ k −
k
Proof. For the sake of brevity denote as p
i
=
D
S,M,s
m
0
[i] and q
i
= D
S,M,s
m
1
[i]. Now, P
i
=
P×p
i
P×p
i
+(1−P)×q
i
.
We consider two cases: i) p
i
≥ q
i
and ii) p
i
< q
i
.
Case 1. p
i
≥ q
i
: It is straightforward to show
that P
i
≥ P. Since
q
i
p
i
−q
i
≥ k, q
i
≥
kp
i
k+1
. Now, P
i
=
Pp
i
Pp
i
+(1−P)q
i
, and this value is maximized when q
i
is
minimized. Thus, P
i
≤
Pp
i
Pp
i
+(1−P)
kp
i
k+1
=
P
P+(1−P)
k
k+1
=
Pk+P
Pk+P+(k−kP)
=
Pk+P
P+k
. Now P
i
−P ≤
Pk+P
P+k
−P =
P−P
2
P+k
.
It is straightforward to show that this value is maxi-
mized when P =
√
k
2
+ k −k.
Case 2. p
i
< q
i
: A symmetrical argument can be
made to case 1.
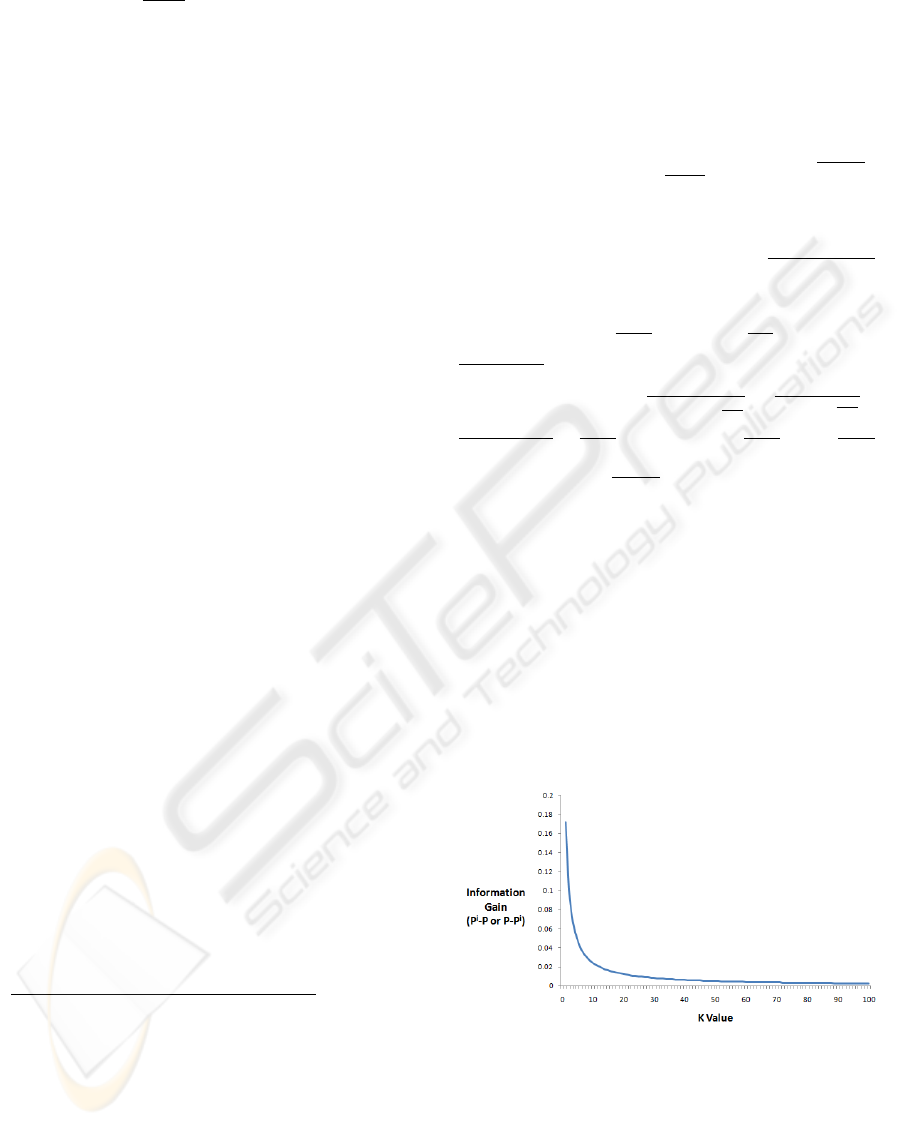
In Figure 1 we plot the the maximal knowledge
gain (i.e., |P
i
−P|) for several value of k. Observe
that, as k increases this value decreases rapidly. For
example, if a scheme satisfies 7-similarity, then a sin-
gle sample changes the adversary’s belief about the
reported value by at most 3.4%, and if the splitting
scheme satisfies 10-similarity, the maximum change
is 2.4%. Clearly, this is not as strong as the notion of
cryptographic privacy, but it may be enough security
in some situations.
Figure 1: Relation between maximum information gain and
K value.
6 A CONSTRUCTION
In this section we present a construction for a splitting
scheme. Before describing the scheme we introduce
a new definition. Define C
s
(T,a,b) to be the number
SECRYPT 2010 - International Conference on Security and Cryptography
236

of ways to choose s values that sum up to T where all
values are in the range [a,b]. Note that these C values
can be computed using the following recurrence:
1. C
1
(T,a,b) = 1 if T ∈ [a,b] and is 0 otherwise.
2. C
i
(T,a,b) =
∑
b
j=a
C
i−1
(T − j,a,b)
The main construction is as follows: At a high
level, to split a value v among s shares, the split-
ting scheme takes as a parameter a value N and pro-
duces values in the range [−N,N]. We discuss how to
choose N later, but clearly it is required that Ns ≥ M.
The scheme chooses q as the first share with proba-
bility
C
s−1
(v−q,−N,N)
C
s
(v,−N,N)
. It then chooses shares for values
v −q using s −1 shares recursively using the same
strategy. Before describing the actual construction,
we need another building block that chooses a value
in a range with the above-specified distribution. This
algorithm is given in Algorithm 1, and the details of
the construction are provided in Algorithm 2.
Algorithm 1: CHOOSE(MIN, MAX,v,s).
1: for i = MIN to MAX do
2: d
i
=
C
s−1
(v−i,MIN,MAX)
C
s
(v,MIN,MAX )
3: end for
4: Choose a value i ∈ [MIN,MAX ] according to dis-
tribution d
MIN
,...,d
MAX
5: return i
Algorithm 2: SPLIT (M, v,s,N).
1: if s = 1 then
2: if v ∈[−N, N] then
3: return < v >
4: else
5: return FAIL/*This will never happen*/
6: end if
7: end if
8: v
s
= CHOOSE(−N, N, v, s)
9: < v
1
,...,v
s−1
>= SPLIT (M,v −v
s
,s −1)
10: return < v
1
,...,v
s
>
In Algorithm 2, notice that if the last share does
not fall into the range [−N,N], then the algorithm will
return FAIL. However, this situation will never hap-
pen, because when we set the ith share to v
i
it must
be possible to obtain v −
∑
i
j=1
v
j
using the remaining
shares. This follows from the probability of that the
ith share is v
i
is:
C
s−i
(v−
∑
i
j=1
v
j
,−N,N)
C
s−i+1
(v−
∑
i−1
j=1
v
j
,−N,N)
, which is 0 if it
is not possible to obtain v −
∑
i
j=1
v
j
with the remain-
ing shares.
Next, let’s look at an example of calculating the
share distributions when N = 2, M = 1, and s = 3.
We use d
j
i
to represent the distribution of share i when
splitting the value j. Then, based on the construction,
when splitting value v = 0, we need to follow the for-
mula below to calculate share i’s distribution:
d
0
i
=
C
2
(0 −i,−2,2)
C
3
(0,−2,2)
Concerning d
0
−1
, for the numerator C
2
(1,−2,2), since
there are four ways(h0,1i,h1,0i,h2,−1i,h−1,2i) to
sum up to 1 with two shares, the value of the numer-
ator will be 4. Then, we can use the same method to
calculate the value of denominator C
3
(0,−2,2) which
is 19, and so the probability of share being value -1 is
4
19
. Using the same method, d
0
−2
=
3
19
, d
0
0
=
5
19
, d
0
1
=
4
19
and d
0
2
=
3
19
. When splitting the value v = 1, the follow-
ing is the share distributions: d
1
−2
=
2
18
, d
1
−1
=
3
18
, d
1
0
=
4
18
,
d
1
1
=
5
18
and d
1
2
=
4
18
.
Using these distributions, we now analyse the de-
gree of k-similarity between these two distributions.
After computing all of these values, the minimum
such k value is 2.375, and thus for these parameters
this construction is 2.375-similar.
If N = (k + 1)M and s = 3, then the scheme
satisfies k-similarity with an amplification factor of
6(k + 1). Due to page constraints we omit the proof
of these claims. We analyse the situation for s > 3 and
the case where t > 1 in experimental section.
• Computation Overhead. One concern with this
splitting scheme is that its time complexity may
not be suitable for a sensor node. Computing the
C values is potentially an expensive step. Dy-
namic programming can be used to compute the
C values. We omit the details of the algorithm,
but it has complexity O(s
2
N
2
), and it is within the
sensor’s computation capability. That is, the val-
ues of s and N are likely to be small enough in
practice to make this practical for a sensor node.
A storage-computation tradeoff is possible; that is
the sensor’s can store the various C values.
• Communication Overhead. We compare
our scheme with both homomorphic encryp-
tion(Castelluccia et al., 2005) and secure aggrega-
tion protocol(Frikken and Dougherty, 2008) that
proposed solutions for solely privacy and integrity
respectively. Specifically in our scheme, the con-
gestion occurred in a single node is O(s). The
scheme in (Castelluccia et al., 2005) results in
O(1) congestion per node, but only provides pri-
vacy. The protocol in (Frikken and Dougherty,
2008) has O(4logN) congestion per node, but
only provides integrity (Here, 4 is the maximum
degree of aggregation tree).
CONFIDENTIALITY AND INTEGRITY FOR SUM AGGREGATION IN SENSOR NETWORKS
237
7 EXPERIMENTS
In this section we describe various experiments that
test the resiliency of the proposed splitting schemes.
We initially focus on the case when a single share is
compromised (i.e., t = 1), but then we consider the
case when t > 1.
7.1 Resiliency against the Single Share
Compromise
Given parameters M, s, and N the level of k-similarity
can be computed as follows: Since the scheme is sym-
metric we need only consider the distribution of the
first share. This distribution is computed as in Algo-
rithm 1. Given this distribution it is straightforward to
compute the k value by finding the i value in [−N,N]
and values m
0
and m
1
in [0,M] that minimize:
min{D
S,M,s
m
0
[i],D
S,M,s
m
1
[i]}
max{D
S,M,s
m
0
[i],D
S,M,s
m
1
[i]}−min{D
S,M,s
m
0
[i],D
S,M,s
m
1
[i]}
for all values i ∈ [−N, N]. This search can be ex-
pedited because this value will be minimized when
m
0
= 0 and m
1
= M (the proof of this claim is omit-
ted due to page constraints).
We now describe the specific experiments:
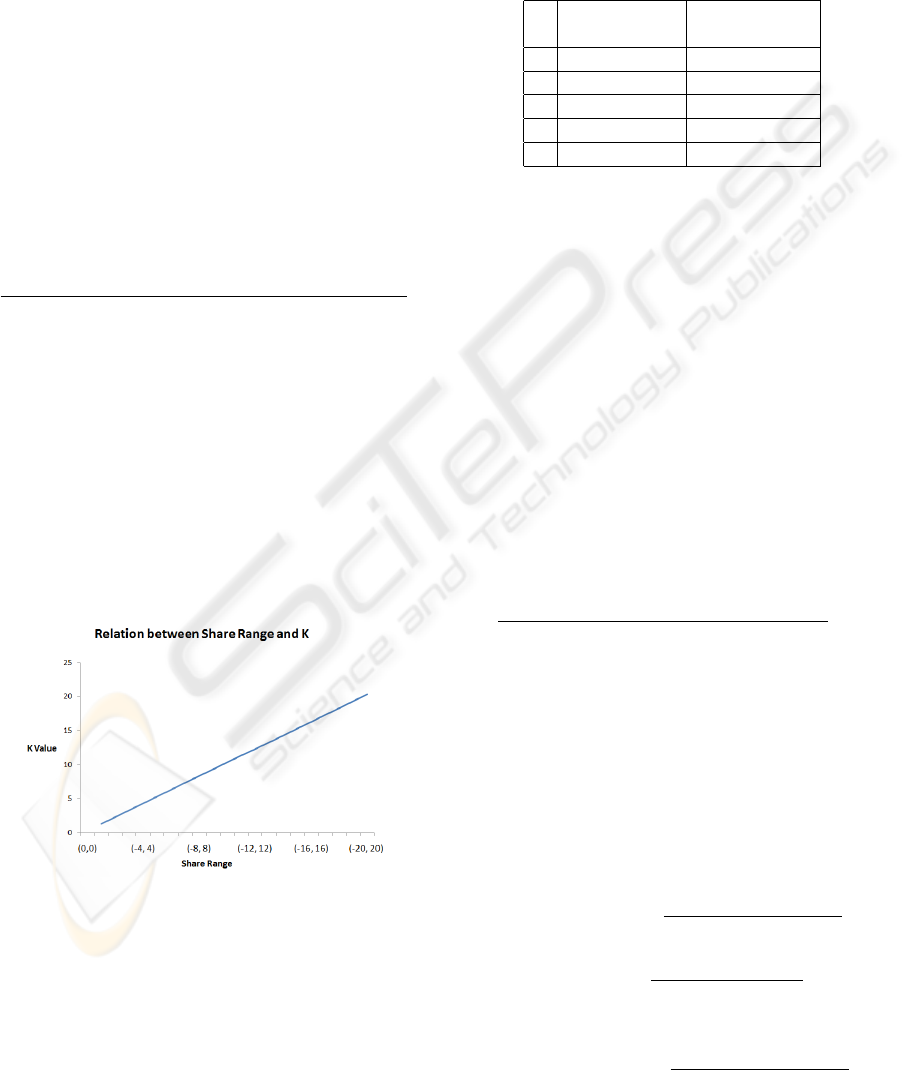
• Relation between Share Ranges and K Value.
In this part, we fix M = 1, s = 3 and varied N from
1 to 20. Figure 2 shows the k value for each value
of N. First it is worth noting that this experiment
validates the claims of section 6. That is if N =
(k + 1)M that the scheme is k-resilient.
Figure 2: Relation between share range and K value.
• Relation between the Number of Shares and K
Value. The goal of this experiment is to deter-
mine the effect of increasing the number of shares.
We fixed M = 1, varied s from 4 to 7, and deter-
mined the minimum N value that was necessary to
achieve k = 10. Table 1 shows the results. It ap-
pears as though the amplification factor is about
the same for all values (except s = 4). Since in-
creasing the number of shares increases the com-
munication, it appears that if the adversary com-
promises only a single cluster head, then s should
probably be chosen as 3.
Table 1: Amplification factor for varied shares.
s Minimum N Amplification
for k = 10 Factor
3 10 30.5
4 10 40.5
5 6 30.5
6 5 30.5
7 4 28.5
7.2 Resiliency against the Collusion
Attack
We now consider the case where the adversary has
more than one share. We generalize the definition of
k-similarity, by looking at the difference in the distri-
butions of t-shares. First, the construction actually
satisfies a stronger definition of symmetry than the
one presented in Definition 2 in that the distribution
of any t shares is the same regardless of which shares
are chosen. Thus we need only consider the distribu-
tion of the first t shares. To formalize this notion if
t = 2, then we let D
S,M,s
m
0
[i, j] be the probability that
two shares will be i and j when splitting the value m
0
.
Thus a scheme is k-similar if for all possible share
values i and j and values m
0
and m
1
:
min{D
S,M,s
m
0
[i, j], D
S,M,s
m
1
[i, j]}
max{D
S,M,s
m
0
[i, j], D
S,M,s
m
1
[i, j]}−min{D
S,M,s
m
0
[i, j], D
S,M,s
m
1
[i, j]}
≥ k
We start with the case where t = 2. Given param-
eters M, s, and N the level of k-similarity can be com-
puted as follows: since the scheme is symmetric we
only need to consider the pair distributions of the first
and the second share, namely Pr[s
1
= i∧s
2
= j](i, j ∈
[−N,N]). The distribution is computed as following:
Pr[s
1
= i ∧s
2
= j] = Pr[s
1
= i|s
2
= j]Pr[s
2
= j]
Based on Algorithm 1, we have
Pr[s
1
= i|s
2
= j] =
C
s−2
(v −i − j, −N, N)
C
s−1
(v − j, −N, N)
Pr[s
2
= j] =
C
s−1
(v − j, −N, N)
C
s
(v,−N,N)
Therefore,
Pr[s
1
= i ∧s
2
= j] =
C
s−2
(v −i − j, −N, N)
C
s
(v,−N,N)
SECRYPT 2010 - International Conference on Security and Cryptography
238

Given this distribution it is straightforward to com-
pute the k value by finding the i and j values in
[−N,N] and values m
0
and m
1
that minimizes the for-
mula in Definition 10. Similar to Section 7.1, these
value will be minimized when m
0
= 0 and m
1
= M.
Figure 3: K values for different number of shares in collu-
sion attack.
• Relation between Number of Shares and K. In
this part, we fix M = 1, t = 2, varied N from 1 to
20, and varied s from 5 to 7. We did not consider s
as 3 or 4, because these provide only 0-similarity.
To be more specific if v = 0 and s = 3, then it is
possible using the construction that 2 shares are
−N and 0 (the 3rd share would be N), but it is not
possible to have 2 shares be −N and 0 when v = 1
(the 3rd share would need to be N + 1, which is
not in the value share range).
Figure 3 shows the results of this experiment.
First, observe that it is possible to obtain reason-
able values of k for these values. Furthermore, it
appears that there is a linear relationship between
N and the k value. Specifically, when s = 5, the
scheme appears to be .5N-resilient, when s = 6,
the scheme appears to be .67N-resilient, and when
s = 7, the scheme appears to be .88N-resilient.
• Relation between Amplification Factor and K.
In this part, we fixed s = 5, t = 2, varied M from
6 to 10, and varied N from 10 to 200. Figure 4
shows the k value for each pair of N and M values.
Again the linear relationship seems to hold, and
it appears as though k is linear in the value
N
M
.
Similar results hold when s is increased (but these
experiments are omitted due to page constraints).
7.2.1 The Case when t > 2
Due to the page limit, we omit from the manuscript
the experiments for when t > 2 shares are com-
promised, but the basic idea is that, we will
compute the distributions for the first t shares
Figure 4: Relation between amplification factor and K value
in collusion attack.
using the formula Pr[s
1
= v
1
∧ s
2
= v
2
∧ ··· ∧
s
n
= v
n
]=
C
s−n
(v−
∑
n
i=1
v
i
,−N,N)
C
s
(v,−N,N)
, and compute the k value
based on Definition 10. Similar results hold in this
case, but the number of shares must be increased.
That is, it must be that s > 2t + 1 in order to have
k-similarity for k > 0.
8 SUMMARY AND FUTURE
WORK
In this paper, we introduced a new integrity measure
and a new privacy measure, called called k-similarity,
which is a weaker notion than cryptographic privacy,
but it is still useful in real applications. Furthermore,
we built a splitting construction that can achieve both
the meaningful privacy and integrity during the SUM
aggregation. And finally, we implemented a series of
experiments to test the effectiveness of our technique
against the adversaries who captured a certain number
of shares. There are several problems for future work,
including:
1. The splitting scheme currently only protects
against leaf nodes reporting false values. While
the scheme could be combined with the approach
in (Roberto et al., 2009) to protect against mali-
cious aggregator nodes, it would be desirable to
create one mechanism that handles both type of
integrity violations. For example, is it possible to
combine the splitting scheme with the scheme in
(Chan et al., 2006) by using different aggregation
trees to obtain similar results.
2. The current scheme doesn’t use expensive cryp-
tography (homomorphic encryption, zero knowl-
edge proofs, etc). Is it possible to obtain crypto-
graphic privacy and constant amplification factor?
Or, is there a different approach that does not use
expensive cryptography that achieves this result?
CONFIDENTIALITY AND INTEGRITY FOR SUM AGGREGATION IN SENSOR NETWORKS
239

3. The analysis in this paper was for the case when
t = 1. However, there appears to be a linear rela-
tionship between the k and N/M. Can this result
be formalized and be proven for t > 1?
ACKNOWLEDGEMENTS
The authors would like to thank the anonymous re-
viewers for their comments and useful suggestions.
Portions of this work were supported by Grant CNS-
0915843 from the National Science Foundation.
REFERENCES
Alzaid, H., Foo, E., and Nieto, J. G. (2008). Secure data
aggregation in wireless sensor network: a survey. In
AISC ’08: Proceedings of the sixth Australasian con-
ference on Information security, pages 93–105, Dar-
linghurst, Australia, Australia. Australian Computer
Society, Inc.
Camtepe, S. A. and Yener, B. (2005). Key distribution
mechanisms for wireless sensor networks: a survey.
Technical report, Rensselaer Polytechnic Institute.
Castelluccia, C., Mykletun, E., and Tsudik, G. (2005). Effi-
cient aggregation of encrypted data in wireless sensor
networks. In MOBIQUITOUS ’05: Proceedings of
the The Second Annual International Conference on
Mobile and Ubiquitous Systems: Networking and Ser-
vices, pages 109–117, Washington, DC, USA. IEEE
Computer Society.
Castelluccia, C. and Soriente, C. (2008). Abba: A balls
and bins approach to secure aggregation in wsns. In
WiOpt’08:Sixth International Symposium on Model-
ing and Optimization in Mobile, Ad Hoc, and Wireless
Networks.
Chan, H., Perrig, A., and Song, D. (2006). Secure hierar-
chical in-network aggregation in sensor networks. In
CCS ’06: Proceedings of the 13th ACM conference on
Computer and communications security, pages 278–
287, New York, NY, USA. ACM.
Frikken, K. B. and Dougherty, IV, J. A. (2008). An effi-
cient integrity-preserving scheme for hierarchical sen-
sor aggregation. In WiSec ’08: Proceedings of the first
ACM conference on Wireless network security, pages
68–76, New York, NY, USA. ACM.
He, W., Liu, X., Nguyen, H., Nahrstedt, K., and Abdelzaher,
T. (2007). Pda: Privacy-preserving data aggregation
in wireless sensor networks. In INFOCOM 2007. 26th
IEEE International Conference on Computer Commu-
nications. IEEE, pages 2045–2053.
Hu, L. and Evans, D. (2003). Secure aggregation for wire-
less networks. In SAINT-W ’03: Proceedings of the
2003 Symposium on Applications and the Internet
Workshops (SAINT’03 Workshops), page 384, Wash-
ington, DC, USA. IEEE Computer Society.
Intanagonwiwat, C., Estrin, D., Govindan, R., and Heide-
mann, J. (2002). Impact of network density on data
aggregation in wireless sensor networks. In ICDCS
’02: Proceedings of the 22 nd International Confer-
ence on Distributed Computing Systems (ICDCS’02),
page 457, Washington, DC, USA. IEEE Computer So-
ciety.
Kamat, P., Zhang, Y., Trappe, W., and Ozturk, C. (2005).
Enhancing source-location privacy in sensor network
routing. In ICDCS ’05: Proceedings of the 25th
IEEE International Conference on Distributed Com-
puting Systems, pages 599–608, Washington, DC,
USA. IEEE Computer Society.
Madden, S., Franklin, M. J., Hellerstein, J. M., and Hong,
W. (2002). Tag: a tiny aggregation service for
ad-hoc sensor networks. SIGOPS Oper. Syst. Rev.,
36(SI):131–146.
Perrig, A., Szewczyk, R., Tygar, J. D., Wen, V., and Culler,
D. E. (2002). Spins: security protocols for sensor net-
works. Wireless Networks, 8(5):521–534.
Przydatek, B., Song, D., and Perrig, A. (2003). Sia: secure
information aggregation in sensor networks. In SenSys
’03: Proceedings of the 1st international conference
on Embedded networked sensor systems, pages 255–
265, New York, NY, USA. ACM.
Roberto, D. P., Pietro, M., and Refik, M. (2009). Confiden-
tiality and integrity for data aggregation in wsn using
peer monitoring. In Security and Communication Net-
works, pages 181–194.
Yang, Y., Shao, M., Zhu, S., Urgaonkar, B., and Cao, G.
(2008). Towards event source unobservability with
minimum network traffic in sensor networks. In WiSec
’08: Proceedings of the first ACM conference on Wire-
less network security, pages 77–88, New York, NY,
USA. ACM.
Yang, Y., Wang, X., Zhu, S., and Cao, G. (2006). Sdap: a
secure hop-by-hop data aggregation protocol for sen-
sor networks. In MobiHoc ’06: Proceedings of the 7th
ACM international symposium on Mobile ad hoc net-
working and computing, pages 356–367, New York,
NY, USA. ACM.
SECRYPT 2010 - International Conference on Security and Cryptography
240
