
IMAGE MOTION ESTIMATION USING OPTIMAL FLOW
CONTROL
Annette Stahl
∗
and Ole Morten Aamo
Department of Engineering Cybernetics, Norwegian University of Science and Technology (NTNU), Norway
Keywords:
Motion estimation, Optimal control, Physical prior, Optimisation.
Abstract:
In this paper we present an optimal control approach for image motion estimation in an explorative and novel
way. The variational formulation incorporates physical prior knowledge by giving preference to motion fields
that satisfy appropriate equations of motion. Although the framework presented is flexible, we employ the
Burgers equation from fluid mechanics as physical prior knowledge in this study. Our control based formula-
tion evaluates entire spatio-temporal image sequences of moving objects. In order to explore the capability of
the algorithm to obtain desired image motion estimations, we perform numerical experiments on synthetic and
real image sequences. The comparison of our results with other well-known methods demonstrates the ability
of the optical control formulation to determine image motion from video and image sequences, and indicates
improved performance.
1 INTRODUCTION
In this work we are concerned with motion estima-
tion of objects in image sequences. The understand-
ing and reconstruction of dynamic motion in image
scenes is one of the key problems in computer vision
and robotics. We present an attempt to adopt control
methods from the field of applied mathematics in a
new form to image sequence processing and to pro-
vide preliminary evaluations of the capability of this
approach.
We describe motion as the displacement vector
field of pixels between consecutive frames of an im-
age sequence. In the literature this is known as opti-
cal flow (Jain et al., 1995). In computer vision local
and global approaches are used to compute the opti-
cal flow field of image sequences. Local approaches
are designed to compute the optical flow at a certain
pixel position by using only the image information in
the local neighbourhood of this specific pixel (Lucas
and Kanade, 1981). Variational optical flow meth-
ods represent global optimisation problems which can
be used to recover the flow field from an image se-
quence as a global minimiser of an appropriate energy
∗
This research was supported by an Alain Bensoussan
fellowship from the European Research Consortium for In-
formatics and Mathematics (ERCIM) and a fellowship from
the Irish Research Council for Science, Engineering and
Technology (IRCSET).
functional. Usually, these energy functionals consist
of two terms: a data term that imposes the result to
be consistent with the measurement (here the bright-
ness constancy assumption) and a regularisation term
which imposes additional constraints like global or
piecewise smoothness to the optical flow field.
One of the first variational methods for motion
analysis was introduced by (Horn and Schunck, 1981)
and incorporates a homogeneous regularisation term,
where the optical flow is enforced to vary smoothly in
space. This leads to an undesired blurring across mo-
tion discontinuities. Therefore, regularisation terms
were introduced to regularise the flow in an image-
driven (Schn¨orr, 1991; Alvarez et al., 1999) or flow-
driven (Deriche et al., 1995) way, where the flow is
prevented from smoothing across object or motion
boundaries, respectively. A systematic classification
of these approaches can be found in (Weickert and
Schn¨orr, 2001a).
Most of the variational approaches incorporate a
purely spatial regularisation of the flow. However,
some efforts have been made to incorporate tempo-
ral smoothness (Nagel, 1990). The work of (We-
ickert and Schn¨orr, 2001b) investigates an extension
of spatial flow-driven regularisation terms to spatio-
temporal flow-driven regularisers. Time is considered
as a third dimension analogue to the two spatial di-
mensions. These approaches improveboth the robust-
ness and the accuracy of the motion estimation but the
14
Stahl A. and Morten Aamo O. (2010).
IMAGE MOTION ESTIMATION USING OPTIMAL FLOW CONTROL.
In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 14-21
DOI: 10.5220/0002937700140021
Copyright
c
SciTePress

flow computation involves the data of the full image
sequence at once.
Note that all these approaches do not incorporate
physical prior knowledge about the motion itself. In
contrast our approach incorporates a space-time regu-
larisation using physical prior knowledge in a control
framework that draws on the literature on the control
of distributed parameter systems in connection with
fluid dynamics (Gunzburger, 2002).
The ideas of two existing control approaches that
are related to motion computation of image sequences
are presented by (Ruhnau and Schn¨orr, 2007) and
(Borzi et al., 2002). Ruhnau and Schn¨orr presented
an optical flow estimation approach for particle im-
age velocimetry that is based on a control formula-
tion subject to physical constraints (Stokes equation).
Their aim is to estimate the velocities of particles in
image sequences of fluids rather than to estimate mo-
tion in every day image scenes.
The basic idea of (Borzi et al., 2002) is to esti-
mate both an optical flow field u and a rectified im-
age function I satisfying the brightness constancy as-
sumption. Note that in their approach Y
k
(and not I)
denotes the sampled images of the image sequence.
The most significant difference to our optical flow ap-
proach is that they do not only estimate the optical
flow u, but also I
k
which is an approximation of the
captured grey value distributions Y
k
, where k speci-
fies the frame number within the image sequence. As
part of the first-order necessary optimality conditions
of the Lagrangian functional their optimal control for-
mulation does not require a differentiation of the im-
age data.
In contrast to that approach, we interpret the grey
values of a scene as a ”fictive fluid” - assuming that its
motion can be described by an appropriate physical
model, in this work realised with the Burgers equa-
tion of fluid mechanics. We adopt the well estab-
lished variational optical flow approach of (Horn and
Schunck, 1981) and add a distributed control exploit-
ing the Burgers equation resulting in a constrained
minimisation problem. The obtained objective func-
tional has to be minimised with respect to the optical
flow and control variables subject to the model equa-
tion over the entire flow domain in space and time.
Our approach estimates not only the optical flow data
from an image sequence, but it also estimates a force
driven by the Burgers equation. The force field in-
dicates the violation of the equation and can indicate
accelerated motions like starting or stopping events or
the change of the motion direction. Therefore one can
exploit this feature as an indicator of unexpected mo-
tion events, taking place in the image sequence.
The initially constrained optimisation problem is
reformulated - exploiting Lagrange multipliers - into
an unconstrained problem allowing to obtain the asso-
ciated first-order optimality system. This results in a
forward-backwardsystem with appropriate initial and
boundary conditions. To solve the optimality system
we uncouple the forward and backward computation
as described in (Gunzburger, 2002) leading to an iter-
ative solution scheme.
2 APPROACH
Before we start to describe the approach in more
detail we first exemplify the notation and components
of our control formulation.
We define a grey value of a certain pixel within
an image sequence by a real valued one-time con-
tinuously differentiable C
1
image function I(x,t),
where x = (x
1
,x
2
)
⊤
denotes the location within some
rectangular image domain Ω and t ∈ [0, T] labels
the corresponding frame at time t. In particular, the
function I(x
1
,x
2
,t) denotes the intensity of a pixel at
position (x
1
,x
2
)
⊤
in the image frame at time t. The
optical flow field is denoted by a two-dimensional
vector field u = (u
1
(x,t),u
2
(x,t))
⊤
, which describes
the intensity changes between images.
We formulate our motion estimation problem
within a variational framework. We minimise an
energy functional E, which consists of a data and a
regularisation term:
Data Term. We make use of the following data term
Z
Ω
(∂
t
I + u· ∇I)
2
dx, (1)
which comprises the optical flow constraint (Horn
and Schunck, 1981) and provides the link between
the given image data, the observed intensity I and the
desired velocity field u. Note that the optical flow
constraint equation represents the requirement that
the intensity of an object point stays constant along
its motion trajectory. Problem (1) is ill-posed as any
vector field u satisfying u· ∇I = −∂
t
I, is a minimiser.
Therefore a regularisation term is added to introduce
additional constraints for the flow field u to obtain an
unique solution.
Regularisation Term. We incorporate the regularisa-
tion term from (Horn and Schunck, 1981)
Z
Ω
α(|∇u
1
|
2
+ |∇u
2
|
2
) dx, 0 < α ∈ R, (2)
to enforce spatial smoothness of the optical flow
field, preferring neighbouring optical flow vectors to
IMAGE MOTION ESTIMATION USING OPTIMAL FLOW CONTROL
15

be similar. The regularisation parameter α adjusts
the relative importance of the smoothness term to
the data term. With an increasing value of α the
vector field is forced to become smoother. We are
aware that regulariser like the L1-regulariser used for
example in (Wedel et al., 2009) allows for sharper
discontinuities in the flow field. Our decision to
use the L2-regulariser in the motion estimation was
mainly driven by the idea to keep the approach clear
and numerically simple. However, the replacement of
the quadratic homogeneous smoothness term could
improve the accurateness of the computed motion
boundaries.
Physical Prior. Considering a constant moving ob-
ject one can determine that structures are transported
by a velocity field and along with it the velocity field
is transported by itself. A physical model equation,
which describes this behaviour is the Burgers equa-
tion and allows to model the movement of rigid ob-
jects.
The inviscid Burgers equation
D
Dt
u = ∂
t
u+ (u· ∇)u= 0 , u(x,0) = u
0
(3)
has been studied and successfully applied for many
decades in aero- and fluid dynamics (Burgers, 1948;
Hirsch, 2000) as a simplified model for turbulence,
boundary layer behaviour, shock wave formation and
mass transport. It contains the convection term from
the fundamental equations of fluid mechanics, the
Navier-Stokes equations.
As a physical interpretation, u in (3) may be
regarded as a vector of conserved (fictive) quantities
or states, with corresponding density functions u
1
,u
2
as components. The material derivative
D
Dt
yields
the acceleration of moving particles. The nonlinear
term (u · ∇)u is known as the inertia term of the
transport process described by (3). See Figure 1 for
an illustration of the transport. We found that our
0.2
0.4
0.6
0.8
1
1.2
1.4
1.6
1.8
Figure 1: Illustration of the transportation of a vector field
with equation (3) at times t = 0,5,10. Gray values visualise
vector magnitudes. Fictive particles move along a shock
front in the lower right direction. In the absence of any
further external information, a region of rarefaction arises
due to mass conservation, acting like a short-time memory.
approach even with the constant velocity assumptions
of our physical prior predicts the non-uniform motion
pattern quite well as shown in our numerical results
(cf. Sec. 4.2).
2.1 Optimal Control Formulation
In the following sections we explain our optimal con-
trol approach. Foundations exploiting fluid dynami-
cal methods can be found in the book of Gunzburger
(Gunzburger, 2002).
We obtain our spatial-temporal control approach
as follows: Additionally to the smoothness term we
introduce a control f, that is distributed in space and
time, which means that it acts over the entire optical
flow domain Ω× [0,T]. The magnitude of the control
is bounded due to penalisation within the objective
functional. The resulting optimisation problem is to
minimise
E(u, f) =
1
2
Z
Ω×[0,T]
n
(∂
t
I + u· ∇I)
2
(4)
+ α(|∇u
1
|
2
+ |∇u
2
|
2
) + β| f|
2
o
dxdt,
subject to the equations of motion
∂
t
u+ (u · ∇)u = f in (0,T) × Ω,
∂
n
u = 0 on (0,T) × Γ.
(5)
We intend to find an optimal state u = (u
1
,u
2
)
⊤
and an optimal control f = ( f
1
, f
2
)
⊤
, such that the
functional E(u, f) is minimised and u and f satisfy
the Burgers equation (5).
The objective of this formulation is to determine
a body force f (the control !) that leads to a velocity
field u which fits to the apparent motion in the image
sequence, and at the same time satisfies physical prior
knowledge in terms of the given equations of motion.
2.2 Optimality System
In order to obtain the velocity field u and the con-
trol f we recast the constrained optimisation problem
(4) - (5) into an unconstrained optimisation problem.
Introducing the Lagrange multiplier or adjoint vari-
able w = (w
1
(x,t),w
2
(x,t))
⊤
yields the following La-
grangian functional
L(u, f,w) = E(u, f) (6)
−
Z
Ω×[0,T]
w
⊤
(∂
t
u+ (u · ∇)u− f) dxdt.
To solve this functional we have to derive the first-
order necessary conditions. This results in the follow-
ing optimality system (7)-(9) from which the optimal
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
16

state u, adjoints w, and the optimal control f can be
determined such that L(u, f,w) is rendered stationary.
∂
t
u+ (u · ∇)u = f in Ω× [0,T],
∂
n
u = 0 on Γ× [0,T],
u|
t=0
= u
0
in Ω,
(7)
−∂
t
w− (u· ∇)w− w∇· u + (∇U)
⊤
w
= ∇I(∂
t
I + u· ∇I) − α∆u in Ω× [0, T],
w = 0 on Γ× [0,T],
w|
t=T
= 0 in Ω,
(8)
βf + w = 0 in Ω × [0,T],
f = 0 on Γ× [0,T],
f|
t=T
= 0 in Ω,
(9)
where (∇U)
⊤
the transposed Jacobian matrix.
The state equation (7) is obtained by derivation of
the Lagrangian functional (6) in the direction of the
Lagrange multiplier, and turns out to be identical to
the Burgers equation (5) itself. The adjoint equation
(8) specifies the first-order necessary conditions
with respect to the state variables u. The optimality
condition (9) is the necessary condition that the
gradient of the objective function – with respect to
the control f – vanishes at the optimum. It also
includes the initial and terminal conditions.
The optimality system (7)-(9) is a coupled system
which turns out to be - due to the large number of
unknowns - prohibitively expensive to solve directly,
but can be solved iteratively as described in the next
section.
2.3 Algorithm
We solve the optimality system (7)-(9) using an itera-
tive gradient descent method (with step length adop-
tion) which decouples the state and adjoint compu-
tation. It consists of the iterative solution of the state
and adjoint equation in such a way that the state equa-
tion is computed forward in time with appropriate ini-
tial condition u
0
and the adjoint equation is computed
backward in time with terminal condition w
t=T
= 0.
The optimality condition is used to update the control
f with the adjoint variable w. The control f is then
used to compute the actual state u. Additionally, the
step length is adjusted ensuring that the actual energy
of the objective functional (4) decreases. Note that we
choose the start value for f to be zero in the very first
iteration.
In our pseudo code description of Algorithm 1,
variable s denotes the step-size that is adapted by the
algorithm and ε the threshold which is used to decide
if the relative difference of the energy is small enough
to be seen as converged.
In the initial step of the algorithm the flow fields
u for all consecutive image frames and the terminal
condition of the adjoint variable for the last frame
(w
t=T
) are set to zero. The first step of the iteration
loop solves the adjoint equation (8) for w backwards
in time using the terminal condition on w and the flow
field u. Then, the optimality condition (9) is used to
update the control field for all frames, allowing the
state equation (8) to be solved for u forward in time
using the new control field. The iteration loop contin-
ues until the decline in E is negligible.
Algorithm 1: Gradient algorithm with automatic step-
length selection.
1: set u = 0, ε = 10
−8
, and s := s
0
(initial step)
2: repeat
3: solve the adjoint equation (8) for w
4: update f: f
m
= f
m−1
− s(β f
m−1
+ w)
5: solve the state equation (7) for u
6: if E(u, f
m
) ≥ E(u, f
m−1
) then
7: s := 0.5s
8: GOTO 4
9: else
10: s := 1.5s
11: end if
12: until |E(u, f
m
) − E(u, f
m−1
)|/|E(u, f
m
)| < ε
3 NUMERICAL SOLUTION
In this part, we summarised the numerical discreti-
sation methods employed in solving the optimality
system (7)-(9). For more details, we refer to (Colella
and Puckett, 1998).
Discretisation of the State Equation. Within the
numerical implementation of the nonlinear state
system equation (7) we have to cope with over-
and undershoots, with shock formations, with the
compliance of conditions (entropy-, monotony-,
CFL-condition, etc.) and different discretisation
schemes. We use the second-order conservative
Godunov scheme for our implementation. The fluxes
are numerically computed by solving the equations at
pixel edges. The correct behaviour at discontinuities
is obtained by using solutions of the appropriate
Riemann problem.
Discretisation of the Adjoint Equation. The
numerical implementation of the time-dependent
adjoint system (8) in the domain Ω is done by using
a second-order predictor-corrector finite difference
IMAGE MOTION ESTIMATION USING OPTIMAL FLOW CONTROL
17

scheme. The basic idea behind this is that all
methods with an accuracy larger than the order one
will produce spurious oscillations in the vicinity of
large gradients, while being second-order accurate
in regions where the solution is smooth. To prevent
such oscillations the slopes of Fromm’s method are
replaced by the slopes of the Van Leers scheme.
The Van Leer scheme detects discontinuities and
modifies its behaviour in such locations accordingly.
The implication of this is that this method retains the
high-order accuracy of Fromm’s scheme in smooth
regions, but near discontinuities the discretised
evolution equation drops to first-order accuracy.
4 EXPERIMENTS
In this section we first illustrate the control perfor-
mance of our optical flow approach on a real-world
2D image sequence. Secondly, we evaluate the
following motions which violate the incorporated
motion assumption: rotation, translation in combi-
nation with scaling. Finally, we present the results
for noisy image data showing the influence of the
temporal regularisation in the control approach and
provide a comparison with error measures obtained
by the approach from (Horn and Schunck, 1981) and
the dynamic optical flow approach from (Stahl et al.,
2006).
4.1 Control - Force
We illustrate the control behaviour of our approach
for a real-world 2D image sequence with an unex-
pected motion. The image sequence consists of 10
image frames and shows a moving hand which starts
to move and then stops again. Figure 2 depicts the
starting (left column) and stopping (right column)
event of the sequence. The first row shows the veloc-
ity estimates u, and the second row shows the force
fields. The force field f nicely indicates the devia-
tion of the expected motion from the observed mo-
tion. This is evident in the second row of Figure 4,
where the force field acts in the direction of the mov-
ing hand as the hand accelerates into motion (left pic-
ture), while it turns in the opposite direction as the
hand stops (right picture).
4.2 Non-uniform Motion
In this section we provide an evaluation of our ap-
proach on the basis of two well known synthetic im-
Figure 2: ”Waving hand” sequence: Unexpected events.
Top: A waving hand stops. The estimated optical flow field
u for a starting (left) and stopping (right) event is depicted in
blue. Bottom: The corresponding control field f is shown
in red. The force acts when the hand starts to move (left)
and reacts into the opposite direction of the flow field (right)
when it stops and forces the flow field into the observed
state of no motion (parameters: α = 0.01, β = 0.0001).
age sequences for which the ground truth motion data
is available. To allow for a quantitative comparison
we provide the results we obtain for the Horn and
Schunck as well. The image sequences we use show
global motion patterns such as rotation, translation
and divergence.
In particular we evaluate our approach on the
grey value versions of the following two image se-
quences: the ”rotating sphere” sequence (McCane
et al., 2001) and the ”Yosemite” sequence (available
at ftp://ftp.csd.uwo.ca/pub/vision).
The ”rotating sphere” sequence contains a curling
vector field and is shown in Figure 3. This sequence
consists of 45 frames, where a sphere rotates in front
of a stationary background.
Figure 3: The synthetic ”rotating sphere” sequence. The
sphere rotates in front of a stationary background. Left:
Gray value version of frame 6 that is used in our computa-
tions. Right: Vector plot of the ground truth data.
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
18

The computed vector fields obtained by the Horn and
Schunck approach and our approach (4)-(5) for the
”rotating sphere” sequence is shown in Figure 4.
Figure 4: The synthetic ”rotating sphere” sequence. Com-
putational Results for the Horn and Schunck approach and
the control based approach. Left: Result Horn and Schunck
(RMSE = 0.395). Right: Result control based approach
(RMSE = 0.192).
The motion estimation results for the ”Yosemite” se-
quence are shown in section 4.3.
The results show that even for sequences which
violate the constant velocity assumption of the model
equation we obtain good results. However, due to
the flexibility of our variational approach it should be
possible to model such motion patterns by incorpora-
tion of a suitable model equation.
4.3 Temporal Regularisation
To investigate the impact of the temporal regularisa-
tion to the robustness of our approach under noise, we
choose the ”Yosemite” sequence with different Gaus-
sian noise levels σ = 0, 10, 20 and 40 (cf. Fig. 5). The
Figure 5: Top Left: Yosemite sequence. Top Right: We
added Gaussian noise with standard deviation σ = 40.
sequence exhibits divergent and translational motion
combined with illumination changes. To investigate
the performance of our approach we compare the root
mean square error (RMSE)
RMSE(u
o
,u
e
) =
1
|Ω|
Z
Ω
q
(u
o
− u
e
)
2
dx
and the average angular error (AAE)
AAE(u
o
,u
e
) =
1
|Ω|
Z
Ω
arccos
u
o
· u
e
|u
o
||u
e
|
dx,
where | · | denotes the Euclidean norm, u
o
=
(u
o
1
,u
o
2
,1)
⊤
the original optical flow vectors, and
u
e
= (u
e
1
,u
e
2
,1)
⊤
the estimated optical flow vectors
(compare (Barron et al., 1994)). Note that the time
dimension is set to 1 corresponding to the distance of
one frame.
This measure is currently used as a kind of stan-
dard to provide accuracy measures for optical flow re-
sults.
We compare the errors of the optical flow compu-
tation obtained for three different approaches with op-
timised parameters. In particular these are the homo-
geneous spatial regularised approach from (Horn and
Schunck, 1981), the spatio-temporal dynamic image
motion approach from (Stahl et al., 2006), and our
control based image motion approach (4) - (5). The
control approach results in a improved vector field,
which is based on the forward-backward computa-
tion, which incorporates additional knowledge of the
future frames leading to an improved temporal regu-
larisation. The result for a single frame in the highly
noisy Yosemite sequence is shown in Figure 6. The
Figure 6: Temporal regularisation. We added Gaussian
noise with standard derivation σ = 40 to the ”Yosemite”
sequence. The shown high quality optical flow field is ob-
tained by the control based optical flow approach (4) - (5)
(parameters: α = 0.05 and β = 0.000003).
results for the computed errors (RMSE and AAE)
for all three approaches with increasing noise level
are shown in Table 1. The purely spatial regularised
approach from Horn and Schunck and the absence
of physical prior knowledge leads to the higher er-
ror values with increasing noise levels. In contrast to
the spatio-temporal dynamic image motion approach
(Stahl et al., 2006) a higher noise level requires the
selection of a smaller β regularisation parameters for
the control part of the objective functional. The con-
sistently lower error indicates an improvedglobal mo-
tion prediction in our control approach (4)-(5) exert-
ing a better temporal regularisation. Our explanation
for this observation is that the control approach incor-
IMAGE MOTION ESTIMATION USING OPTIMAL FLOW CONTROL
19
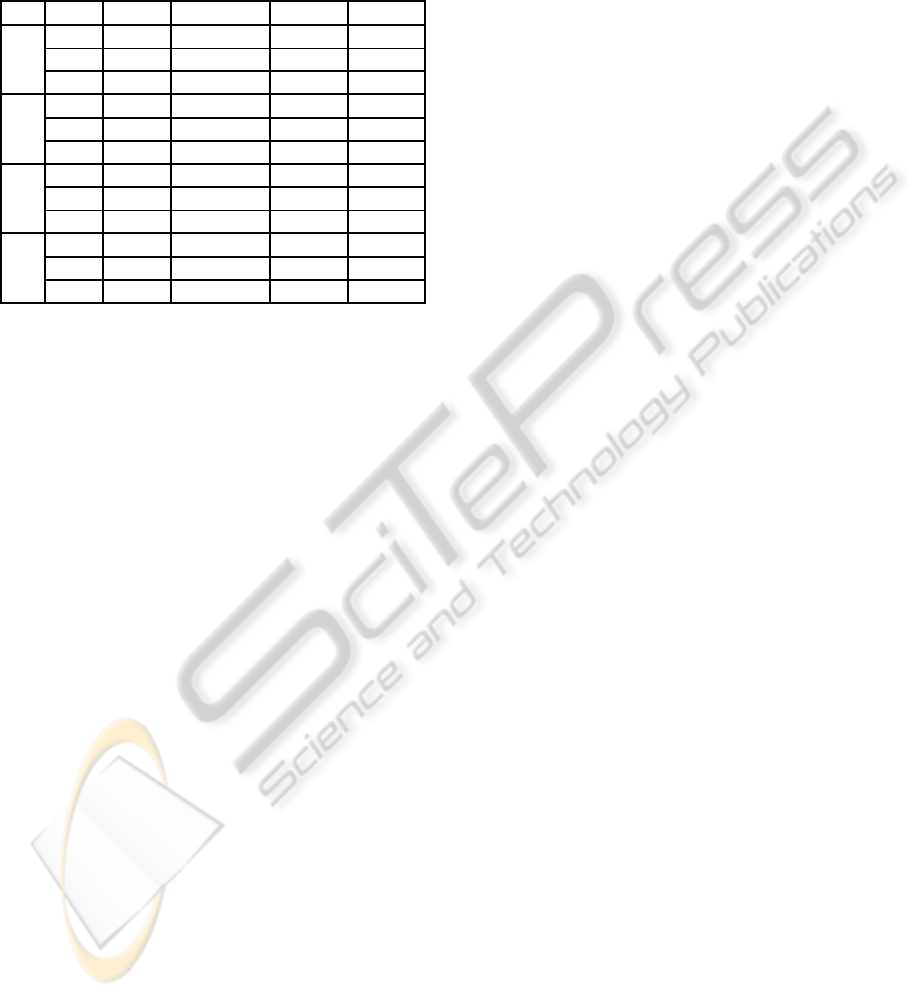
Table 1: Performance of our control approach (C) in com-
parison with the Horn and Schunck approach (HS) and the
dynamic image motion approach (Dy) in presence of noise:
We added random Gaussian noise with zero mean and stan-
dard deviation σ = 0, 10, 20, and 40 to the Yosemite image
sequence.
σ app. α β RMSE AAE
0 HS 0.005 - 0.177 3.04
◦
Dy 0.006 0.00002 0.178 3.09
◦
C 0.007 0.0005 0.169 2.88
◦
10 HS 0.008 - 0.283 5.74
◦
Dy 0.01 0.0003 0.275 5.68
◦
C 0.009 0.0001 0.243 4.92
◦
20 HS 0.02 - 0.429 8.61
◦
Dy 0.025 0.001 0.395 7.54
◦
C 0.02 0.00001 0.350 6.67
◦
40 HS 0.05 - 0.640 13.27
◦
Dy 0.05 0.005 0.523 9.89
◦
C 0.05 0.000003 0.497 9.16
◦
porates also future knowledge of the image sequence
instead of using only past information with a predic-
tion as in (Stahl et al., 2006).
5 CONCLUSIONS
We have presented an optimal control approach to
image motion estimation including physical prior
knowledge in a novel and exploratory way. It leads to
an unconstrainedoptimisation problem, where the op-
timality system - from which the optimal state and the
optimal control are determined - can be solved using
an iterative gradient descent method. The forward-
backward structure of the model allows for a robust
estimation of the coherent flows by including prior
knowledge that enforce spatio-temporal smoothness
of the minimising vector field.
In the case that the image measurements indicate
changes of the current velocity distribution, fictive
control forces modify the system state accordingly.
The presence of such forces may serve as an indicator
notifying a higher-level processing stage about unex-
pected motion events in video sequences.
The comparison of our results with the approach
from (Horn and Schunck, 1981) and the approach
from (Stahl et al., 2006) demonstrates the ability of
the control formulation to determine image motion
from video sequences, and shows improved perfor-
mance, especially for highly noisy image data. Our
further work will include the modification of the
Burgers equation to achieve better motion boundaries
in the rarefaction area and the reformulation of the
approach to a receding horizon formulation.
ACKNOWLEDGEMENTS
We would like to thank Dr. Christian Schellewald,
Dr. Paul Ruhnau, Prof. Christoph Schn¨orr, and Prof.
Øyvind Stavdahl for some inspiring discussions and
comments.
REFERENCES
Alvarez, L., Esclar`ın, J., Lefebure, M., and S`anchez, J.
(1999). A PDE model for computing the optical flow.
In Proceedings of CEDYA XVI, pages 1349–1356.
Barron, J. L., Fleet, D. J., and Beauchemin, S. S. (1994).
Performance of optical flow techniques. Int. J. of
Computer Vision, 12(1):43–77.
Borzi, A., Ito, K., and Kunisch, K. (2002). Optimal control
formulation for determining optical flow. SIAM J. Sci.
Comput., 24(3):818–847.
Burgers, J. M. (1948). A mathematical model illustrating
the theory of turbulence. Adv. Appl. Mech., 1:171–
199.
Colella, P. and Puckett, E. G. (1998). Modern Nu-
merical Methods for Fluid Flow. Lecture Notes,
Dep. of Mech. Eng., Uni. of California, Berke-
ley, CA. http://www.rzg.mpg.de/ bds/numerics/cfd-
lectures.html.
Deriche, R., Kornprobst, P., and Aubert, G. (1995). Optical-
flow estimation while preserving its discontinuities: A
variational approach. In ACCV, pages 71–80.
Gunzburger, M. (2002). Perspectives in Flow Control
and Optimization. Society for Industrial and Applied
Mathematics.
Hirsch, C. (2000). Numerical Computation of Internal and
External Flows (Vol.I+II). John Wiley & Sons.
Horn, B. and Schunck, B. (1981). Determining optical flow.
Artificial Intelligence, 17:185–203.
Jain, R., Kasturi, R., and Schunck, B. G. (1995). Machine
Vision. McGraw-Hill, Inc.
Lucas, B. D. and Kanade, T. (1981). An iterative image reg-
istration technique with an application to stereo vision
(darpa). In Proc. of the 1981 DARPA Image Under-
standing Workshop, pages 121–130.
McCane, B., Novins, K., Crannitch, D., and Galvin, B.
(2001). On benchmarking optical flow. Comput. Vis.
Image Underst., 84(1):126–143.
Nagel, H. H. (1990). Extending the ‘oriented smoothness
constraint’ into the temporal domain and the estima-
tion of derivatives of optical flow. In Proc. of the first
european conf. on computer vision, pages 139–148.
Springer.
Ruhnau, P. and Schn¨orr, C. (2007). Optical Stokes flow:
An imaging-based control approach. Experiments in
Fluids, 42:61–78.
Schn¨orr, C. (1991). Determining optical flow for irregular
domains by minimizing quadratic functionals of a cer-
tain class. Int. J. of Computer Vision, 6(1):25–38.
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
20

Stahl, A., Ruhnau, P., and Schn¨orr, C. (2006). A Distributed
Parameter Approach to Dynamic Image Motion. Int.
Workshop on The Representation and Use of Prior
Knowledge in Vision. ECCV Workshop.
Wedel, A., Pock, T., Zach, C., Bischof, H., and Cremers,
D. (2009). An improved algorithm for tv-l1 optical
flow. In Statistical and Geometrical Approaches to
Visual Motion Analysis: International Dagstuhl Semi-
nar, Dagstuhl Castle, Germany, July 13-18, 2008. Re-
vised Papers, pages 23–45. Springer-Verlag.
Weickert, J. and Schn¨orr, C. (2001a). A theoretical frame-
work for convex regularizers in PDE-based compu-
tation of image motion. Int. J. of Computer Vision,
45(3):245–264.
Weickert, J. and Schn¨orr, C. (2001b). Variational optic flow
computation with a spatio-temporal smoothness con-
straint. J. Math. Imaging and Vision, 14(3):245–255.
IMAGE MOTION ESTIMATION USING OPTIMAL FLOW CONTROL
21
