ASYMPTOTIC ANALYSIS OF PHASE CONTROL SYSTEM FOR
CLOCKS IN MULTIPROCESSOR ARRAYS
G. A. Leonov, S. M. Seledzhi
Saint-Petersburg State University, Universitetski pr. 28, Saint-Petersburg, 198504, Russia
N. V. Kuznetsov, P. Neittaanm¨aki
University of Jyv¨askyl¨a, P.O. Box 35 (Agora), FIN-40014, Finland
Keywords:
Array processors, Clock generator, Phase-locked loop, Stability.
Abstract:
New method for the rigorous mathematical analysis of electronic synchronization systems is suggested. This
method allows to calculate the characteristics of phase detectors and carry out a rigorous mathematical analysis
of transient process and stability of the system.
1 INTRODUCTION
In recent years, it has actively produced and used
array processors systems, which face the problem
of generation of synchronous signals and the mutual
synchronization of processors.
In realizing parallel algorithms, the processors
must perform a certain sequence of operations si-
multaneously. These operations are to be started at
the moments of arrival of clock pulses at processors.
Since the paths along which the pulses run from the
clock to every processor are of different length, a
mistiming in the work of processors arises. This phe-
nomenon is called a clock skew.
The elimination of the clock skew is one of the
most important problems in parallel computing and
information processing (as well as in the design of
array processors).
Several approaches to solving the problem of
eliminating the clock skew have been devised for the
last thirty years.
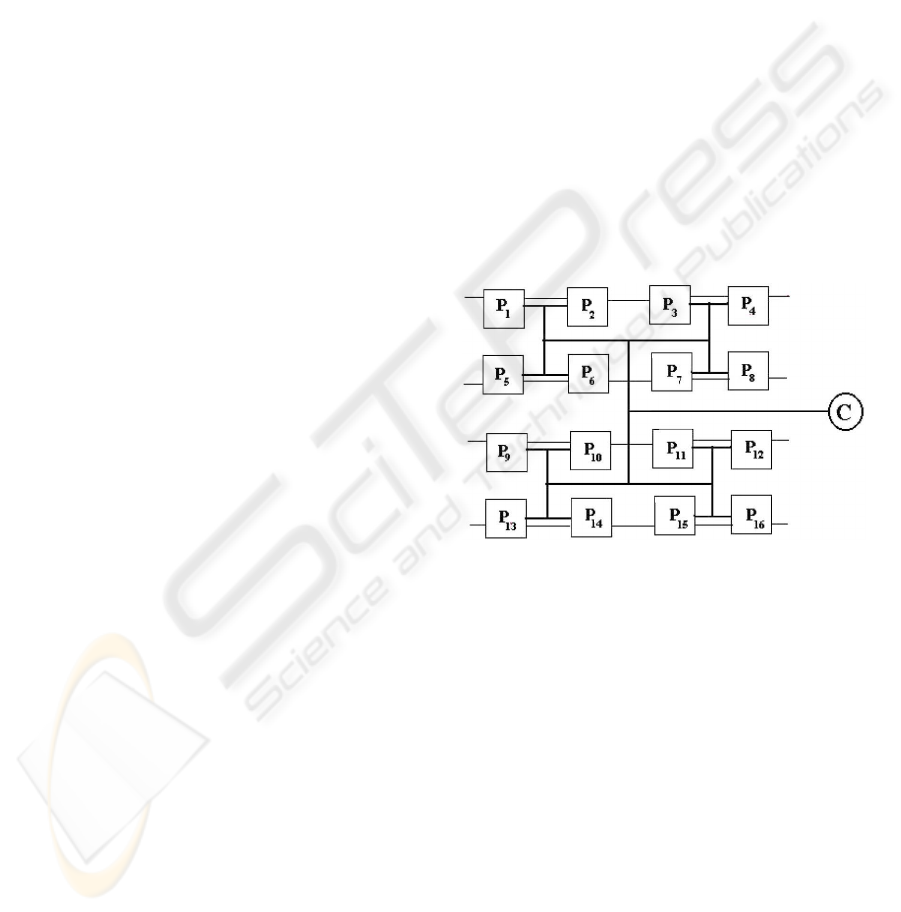
In developing the design of multiprocessor sys-
tems, a way was suggested Kung, 1988 for joining
the processors in the form of an H-tree, in which (Fig.
1) the lengths of the paths from the clock to every pro-
cessor are the same. However, in this case the clock
skew is not eliminated completely because of hetero-
geneity of the wires (Kung, 1988). Moreover, for a
great number of processors, the configuration of com-
munication wires is very complicated. This leads to
difficult technological problems.
Among the disadvantages we note the decelera-
Figure 1: H-tree.
tion of performance of parallel algorithms. In addi-
tion to the problem of eliminating the clock skew, an-
other important problem arose. The increase in the
number of processors in multiprocessor systems re-
quired an increase in the power of the clock. But the
powerful clock came to produce significant electro-
magnetic noise. Not so long ago a new method for
eliminating the clock skew and reducing the genera-
tor’s power was suggested. It consists of introducing
a special distributed system of clocks controlled by
phase-locked loops (Fig. 2). This approach enables
one to reduce significantly the power of clocks.
Phase-locked loops (PLLs) are widely used in
telecommunication and computer architectures. They
were invented in the 1930s-1940s (De Bellescize,
1932; Wendt & Fredentall, 1943) and then the the-
ory and practice of PLLs were intensively studied
(Viterbi, 1966; Lindsey, 1972; Gardner, 1979).
99
A. Leonov G., M. Seledzhi S., Neittaanmäki P. and V. Kuznetsov N. (2010).
ASYMPTOTIC ANALYSIS OF PHASE CONTROL SYSTEM FOR CLOCKS IN MULTIPROCESSOR ARRAYS.
In Proceedings of the 7th International Conference on Informatics in Control, Automation and Robotics, pages 99-102
DOI: 10.5220/0002938200990102
Copyright
c
SciTePress
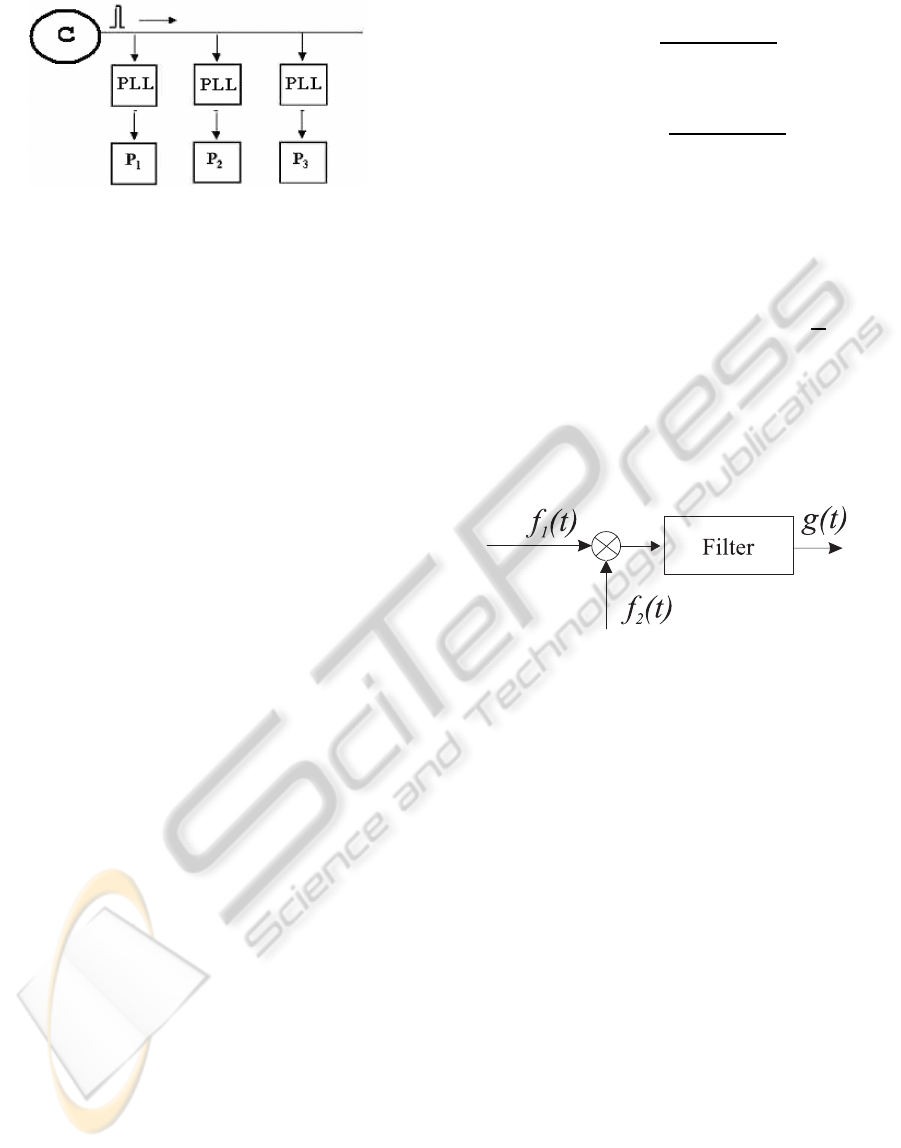
Figure 2: Distributed system of clocks controlled by PLLs.
Various methods for analysis of phase-locked
loops are well developed by engineers and considered
in many publications (see, e.g., (Best, 2003; Kroupa,
2003; Egan, 2007)) but the problems of construction
of adequate nonlinear models and nonlinear analy-
sis of such models are still far from being resolved
and require using special methods of qualitative the-
ory of differential, difference, integral, and integro-
differential equations (Leonov et al., 1992; Leonov
et al., 1996; Abramovitch, 2002; Margaris, 2004;
Kudrewicz & Wasowicz, 2007; Kuznetsov, 2008;
Leonov, 2006).
In this paper new method for the rigorous math-
ematical analysis of electronic synchronization sys-
tems is suggested. This method consists in consider-
ing a phase synchronization system on three levels:
1) a level of electronic realizations;
2) a level of phase and frequency relations be-
tween inputs and outputs in block diagrams;
3) a level of differential and integro-differential
equations, and performing the asymptotic analysis of
high-frequency periodic oscillations.
This method allows one to calculate the char-
acteristics of phase detectors and make a rigorous
mathematical analysis of transient and stability of
the system (Leonov, 2006; Kuznetsov et al., 2008;
Kuznetsov et al., 2009; Leonov et al., 2009).
2 ASYMPTOTIC ANALYSIS AND
PHASE DETECTORS
CHARACTERISTICS
CALCULATION
Consider a differentiable 2π-periodic function g(x),
having two and only two extremums on [0, 2π] : g
−
<
g
+
, and the following properties.
For any number α ∈ (g
−
, g
+
) there exist two and
only two roots of the equation g(x) = −α:
0 < β
1
(α) < β
2
(α) < 2π.
Consider the function
F(α) = 1−
β
2
(α) − β
1
(α)
π
if g(x) < −α on (β
1
(α), β
2
(α)) and the function
F(α) = −
1−
β
2
(α) − β
1
(α)
π
if g(x) > −α on (β
1
(α), β
2
(α)) and a < b, ω.
Suppose, ω is sufficiently large relative to the
numbers a, b, α, π.
Lemma 1. The following relation
b
Z
a
sign[α + g(ωt)]dt = F(α)(b− a) + O(
1
ω
) (1)
is satisfied.
Lemma 1 results from the formula for definitions
of F(α).
Consider now the propagation of pulse high-
frequency oscillations through linear filter (Fig. 3)
Figure 3: Multiplicator and filter.
Here
f
j
(t) = A
j
sign sin(ω
j
(t)t + ψ
j
), (2)
g(t) = α(t) +
t
Z
0
γ(t − τ) f
1
(τ) f
2
(τ)dτ, (3)
⊗ is a multiplicator, A
j
> 0, ψ
j
are certain constants,
j = 1, 2, γ(t) is a impulse response of linear filter and
α(t) is an exponentially damped function, linearly de-
pending on initial state of filter at moment t = 0.
A high-frequency property of generators can be
reformulated as the following condition.
Consider a large fixed time interval [0, T], which
can be partitioned into small intervals of the form
[τ, τ + δ], (τ ∈ [0, T]),
where the following relations
|γ(t) − γ(τ)| ≤ Cδ, |ω
j
(t) − ω
j
(τ)| ≤ Cδ,
∀t ∈ [τ, τ+ δ], ∀τ ∈ [0, T],
(4)
|ω
1
(τ) − ω
2
(τ)| ≤ C
1
, ∀τ ∈ [0, T], (5)
ω
j
(τ) ≥ R, ∀τ ∈ [0, T], (6)
are satisfied.
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
100
We shall assume that δ is small enough relative to
the fixed numbers T,C,C
1
and R is sufficiently large
relative to the number δ : R
−1
= O(δ
2
).
The latter means that on small intervals [τ, τ + δ]
the functions γ(t) and ω
j
(t) are ”almost constant”
and the functions f
j
(t) on them are rapidly oscillat-
ing. Obviously, such a condition occurs for high-
frequency oscillations.
Consider now 2π-periodic function ϕ(θ) of the
form
ϕ(θ) = A
1
A
2
1−
2|θ|
π
, θ ∈ [−π, π] (7)
and a block-scheme in Fig. 4
Figure 4: Phase detector and filter.
Here θ
j
(t) = ω
j
(t)t + ψ
j
are phases of the oscil-
lations f
j
(t), PD is a nonlinear block with the char-
acteristic ϕ(θ) (being called a phase detector or dis-
criminator) with the output
G(t) = α(t) +
t
Z
0
γ(t − τ)ϕ(θ
1
(τ) − θ
2
(τ))dτ. (8)
Theorem 1. If conditions (4)–(6) are satisfied, then
for the same initial states of filter we have
|G(t) − g(t)| ≤ Dδ, ∀t ∈ [0, T]. (9)
Here D is a certain not depending on δ number.
Proof. It is readily seen that
g(t) − α(t) =
t
Z
0
γ(t − s)A
1
A
2
sign[cos((ω
1
(s)−
−ω
2
(s))s+ ψ
1
− ψ
2
) − cos((ω
1
(s) + ω
2
(s))s+
+ψ
1
+ ψ
2
)]ds =
=A
1
A
2
m
∑
k=0
γ(t − kδ)
(k+1)δ
Z
kδ
sign[cos((ω
1
(kδ) −
−ω
2
(kδ))kδ + ψ
1
− ψ
2
) − cos((ω
1
(kδ) + ω
2
(kδ))s+
+ψ
1
+ ψ
2
)]ds+ O(δ
2
)
i
, t ∈ [0, T].
Here the number m is such that
t ∈ [mδ, (m+ 1)δ].
By Lemma 1 this implies the estimate
g(t) = α(t) + A
1
A
2
m
∑
k=0
γ(t − kδ)ϕ(θ
1
(kδ)−
− θ
2
(kδ))δ
+ O(δ) = G(t) + O(δ).
This relation proves the assertion of Theorem 1.
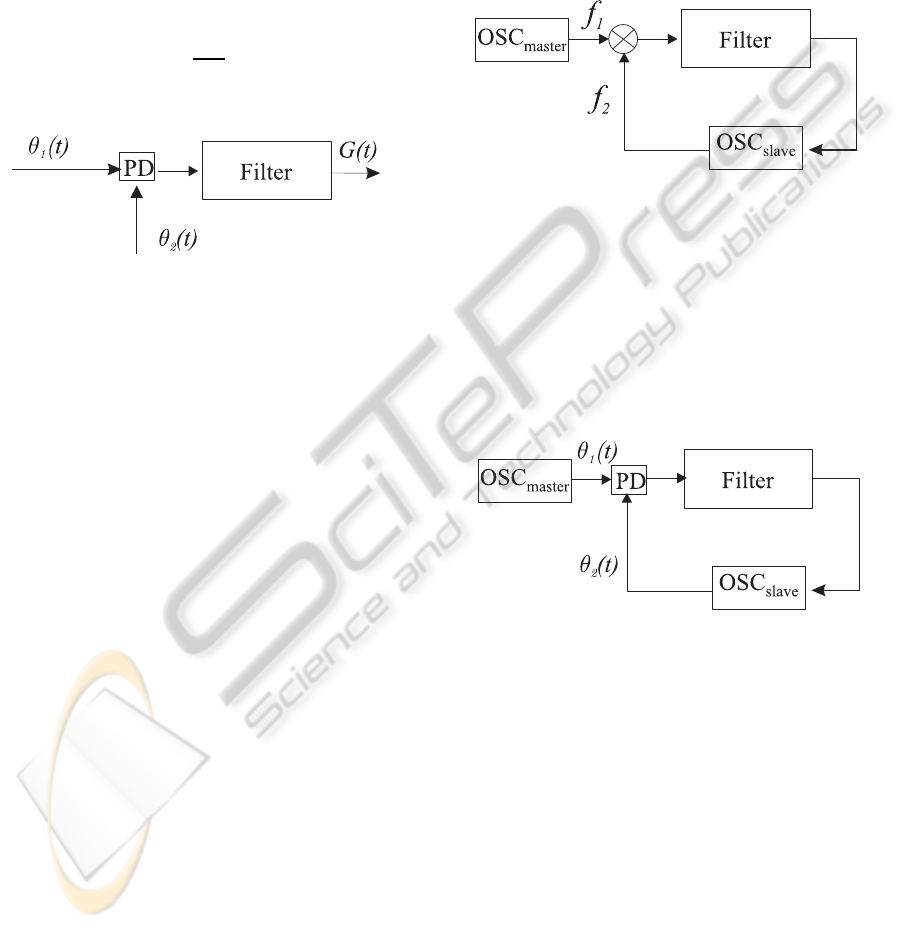
Consider now a block-scheme of typical phase-
locked loop [1–6] (Fig. 5)
Figure 5: Phase-locked loop with multiplicator.
Here OSC
master
is a master oscillator, OSC
slave
is a
slave (tunable) oscillator and block
N
is a multiplier
of oscillations of f
1
(t) and f
2
(t).
From Theorem 1 it follows that for pulse gen-
erators, at the outputs of which there are produced
signals (2), this block-scheme can be asymptotically
changed (for high-frequency generators) to a block-
scheme on the level of frequency and phase relations
(Fig. 6)
Figure 6: Phase-locked loop with phase detector.
Here PD is a phase detector with characteristic (7).
Thus, here on basis of asymptotical analysis of
high-frequencypulse oscillations (Lemma 1 and The-
orem 1) a characteristic of phase detector (7) is com-
puted.
We give now a scheme for computing characteris-
tics of phase detector for PLL with squarer. Consider
a block-scheme in Fig. 1 with
f
1
(t) = A
2
1
(1+ signsin(ω
1
(t)t + ψ
1
))
2
f
2
(t) = A
2
signsin(ω
2
(t)t + ψ
2
)
Consider then a block-scheme in Fig. 2, where PD
is a block with characteristic F(θ) = 2A
1
ϕ(θ).
Theorem 2. If conditions (4)–(6) are satisfied, then
for the same initial states of filter the relation
|G(t) − g(t)| ≤ Dδ, t ∈ [0, T]
ASYMPTOTIC ANALYSIS OF PHASE CONTROL SYSTEM FOR CLOCKS IN MULTIPROCESSOR ARRAYS
101

holds true. Here D is a certain independent of δ num-
ber.
Proof of Theorem 2 is similar to that of Theorem 1.
Finally it may be remarked that for modern pro-
cessors a transient process time in PLL is less than or
equal to 10 sec. and a frequency of clock oscillators
attains 10Ghz . Given δ = 10
−4
(i.e. partitioning each
second into thousand time intervals), we obtain an ex-
pedient condition for the proposed here asymptotical
computation of phase detectors characteristics:
ω
−1
= 10
−10
= 10
−2
(δ
2
) = O(δ
2
).
3 CONCLUSIONS
Thus consideration of phase synchronization system
at three levels (electronic realizations; phase and fre-
quency relations differential and integro-differential
equations) make it possible to calculate the charac-
teristics of the phase detector and perform rigorous
mathematical analysis of the stability of the system.
ACKNOWLEDGEMENTS
This work was supported by projects of Federal Pro-
gram ”Scientific and scientific-pedagogical cadres In-
novative Russia” in 2009 - 2013 years.
REFERENCES
Kung, S. (1988). VLSI Array Processors, Prentice Hall
Lindsey, W. (1972). Synchronization systems in communi-
cation and control, Prentice-Hall. New Jersey.
Viterbi, A. (1966). Principles of coherent communications,
McGraw-Hill. New York.
Gardner, F. (2005). Phase–lock techniques, John Wiley &
Sons, New York, 2
ed
.
Best Ronald, E. (2003). Phase-Lock Loops: Design, Simu-
lation and Application, McGraw Hill, 5
ed
.
Egan, W. F. (2000). Frequency Synthesis by Phase Lock,
(2nd ed.), John Wiley and Sons, 2
ed
.
Kroupa, V. (2003). Phase Lock Loops and Frequency Syn-
thesis, John Wiley & Sons.
Leonov, G., Reitmann, V., Smirnova, V. (1992). Nonlocal
Methods for Pendulum-Like Feedback Systems, Teub-
ner Verlagsgesselschaft. Stuttgart; Leipzig.
Leonov, G., Ponomarenko, D., Smirnova, V. (1996).
Frequency-Domain Methods for Nonlinear Analysis.
Theory and Applications, World Scientific. Singapore.
Abramovitch, D. (2002). Phase-Locked Loope A control
Centric. Tutorial, Proceedings of the American Con-
trol Conference 2002. vol. 1, pp. 1–15
Margaris, N. I. (2004). Theory of the Non-Linear Analog
Phase Locked Loop, Springer Verlag
Kudrewicz, J. and Wasowicz S. (2007). Equations of
Phase-Locked Loops: Dynamics on theCircle, Torus
and Cylinder, World Scientific
Kuznetsov, N. V., (2008). Stability and Oscillations of Dy-
namical Systems: Theory and Applications Jyv¨askyl¨a
Univ. Printing House.
Leonov, G. A., (2006). Phase synchronization. Theory and
Applications Automation and remote control, N 10,
pp. 47–85. (survey)
Kuznetsov, N. V., Leonov, G.A., Seledzhi, S.M. (2008).
Phase Locked Loops Design And Analysis, Interna-
tional Conference on Informatics in Control, Automa-
tion and Robotics, Madeira, Portugal, pp. 114–118.
Kuznetsov, N. V., Leonov, G.A., Seledzhi, S.M., Neittaan-
maki, P. (2009). Analysis and design of computer ar-
chitecture circuits with controllable delay line, Infor-
matics in Control, Automation and Robotics, 2009,
Proceedings, Vol. 3 - Signal processing, Systems
Modeling and Control, pp. 222–224.
Leonov, G., Kuznetsov, N., Seledzhi S. (2010). Nonlinear
Analysis and Design of Phase-Locked Loops, Chap-
ter in the book Automation and Control - Theory And
Practice, In-Tech, 2010 [in print]
ICINCO 2010 - 7th International Conference on Informatics in Control, Automation and Robotics
102
